|
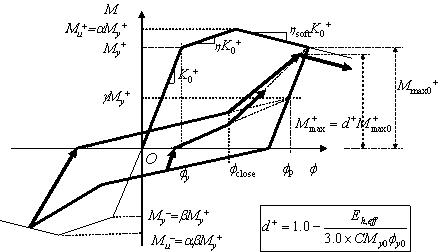
通过MSC.MARC的UBEAM程序,可以将陆新征-曲哲模型嵌入到MSC.MARC程序中,得到陆新征-曲哲模型塑性铰程序。陆新征-曲哲模型塑性铰程序的主要注意事项:
(1) 使用MSC.MARC 98号梁单元;
(2) 建立Matcode.txt数据文件,输入塑性铰信息。参考SAP2000的做法,每个内力份量输入一个行塑性铰,从上到下分别是N,
Vx, Vy, Mx, My,
T。如果需要考虑该内力份量的非线性,则需输入所有的8个参数(初始刚度K0,屈服强度My,强化模量h和损伤累计耗能参数C,滑移捏拢参数g,软化参数hsoft,极限强度参数a,正负向强度比参数b),否则只需输入K0,后面留空,程序自动按弹性处理。
如所附算例中,只需考虑梁局部坐标系y方向的塑性铰,则对应的Matcode输入为:
|
输入内容
|
含义
|
|
! 截面01,梁
3.00D+09,
1.00d+15,
1.00d+15,
5.00E+12,
3.49E+13,1.0e8,0.02,1000,0.8, -0.01, 1.05,1.0
3.99E+13
|
第1行,注释
第2行,N
第3行,Vx
第4行,Vy
第5行,Mx
第6行,My
第7行,T
|
(3) 在前处理中,选择User
Defined Var #1~6,分别对应于N, Vx, Vy,
Mx, My, T的塑性铰标识。
例如,对所附算例输入以下柱铰和梁铰参数,
梁的塑性铰参数为:3.49E+13,1.0e8,0.02,1000,0.8, -0.02, 1.05,1.0
柱的塑性铰参数为:2.33E+13,1.6e8,0.10,100,0.2, -0.05, 1.05,1.0
进行Kobe波下的时程分析,得到柱脚弯矩曲率关系,梁铰弯矩曲率关系以及结构顶点位移-时程关系如图3~5所示,塑性铰分布如图6所示:
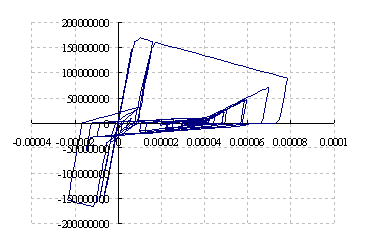
图3 柱脚弯矩曲率关系
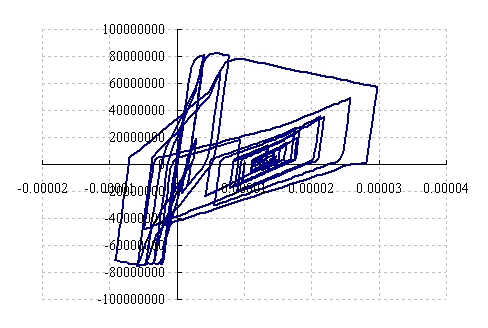
图4 梁铰弯矩曲率关系
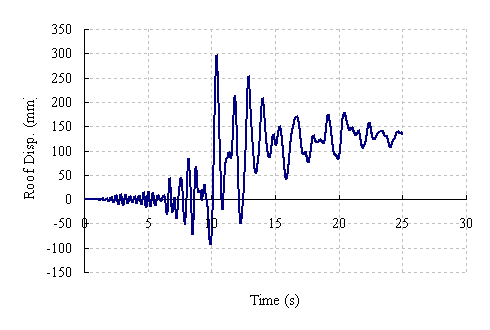
图5 顶点位移时程关系
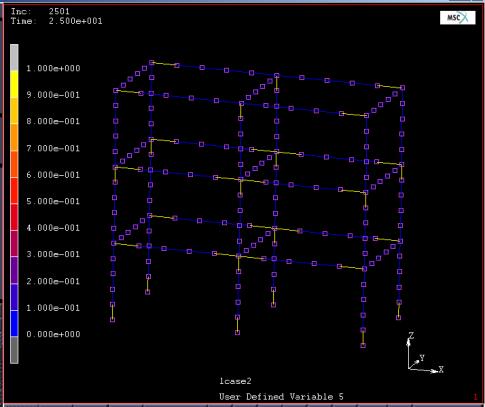
图6 塑性铰分布
附录:框架建模过程
两层混凝土框架,柱子间距为x方向5m,Y方向4m,层高3m。
梁:截面尺寸0.2×0.5m,My= 1.0E8,其他内力分量保持弹性。
柱:截面尺寸0.3×0.4m,My= 1.6E8,其他内力分量保持弹性。。
THUFIBER程序使用时,用户需要输入以下两类信息:
(1)构件的截面几何信息和局部坐标系信息,这部分通过MSC.MARC自带的前处理界面实现,其中最重要的信息有三个:截面面积、材料密度和截面x轴的方向。程序将根据前两条信息计算得到构件的质量。根据截面x轴方向计算其强轴和弱轴行为。
(2)构件截面塑性铰信息,这部分存放在matcode.txt文件中。
下面介绍具体建模步骤:
(1)MSC.MARC程序和多种CAD软件有着良好的接口,以广泛使用的AutoCAD程序为例,在AutoCAD中建立结构的轴线模型如图7所示。将模型文件输出为dxf格式。
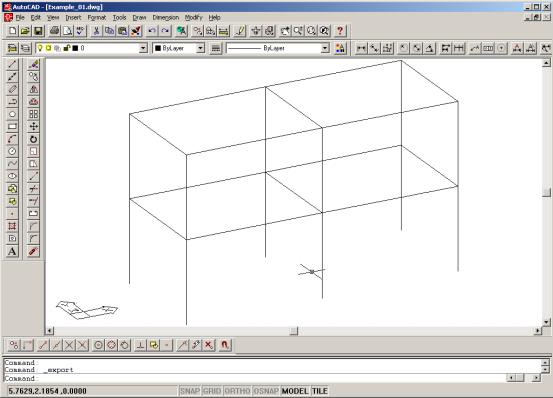
图7在AutoCAD中建立空间模型
(2)在MSC.MARC的前处理程序MENTAT中,选择底部的静态菜单FILE->IMPORT,选择输入DXF格式,选择相应文件,读入刚才的CAD模型,并用底部静态菜单做适当旋转,结果如图8所示。
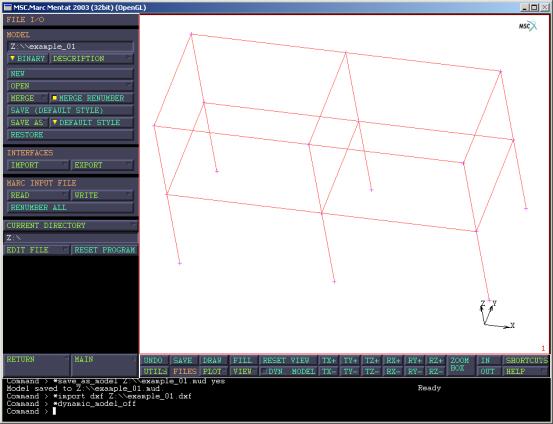
图8 将AutoCAD模型导入MARC
(3)目前在有限元程序中读入的模型还是几何信息,需要将其转化为有限元信息。进入MARC的主菜单MESH
GENERATION,选择CONVERT,将DIVISIONS设置为5,5,即每个线段划分成5个单元。选择CURVERS
TO ELEMENTS,选择ALL:
EXIST,得到单元和节点分布如图9所示。
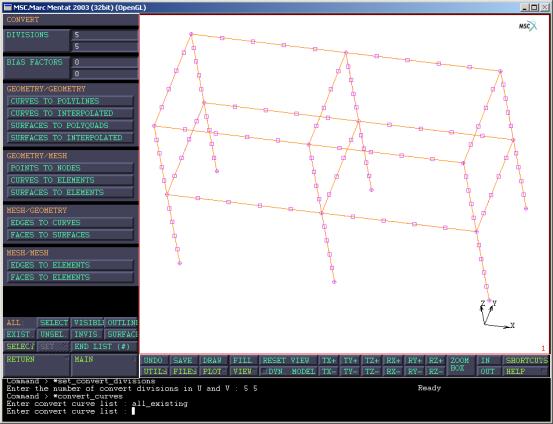
图9 将单元细分
(4) 回到主菜单MAIN MENU->MESH GENERATION,选择SWEEP按钮,选择ALL,清理不必要的节点和单元信息(图10)。
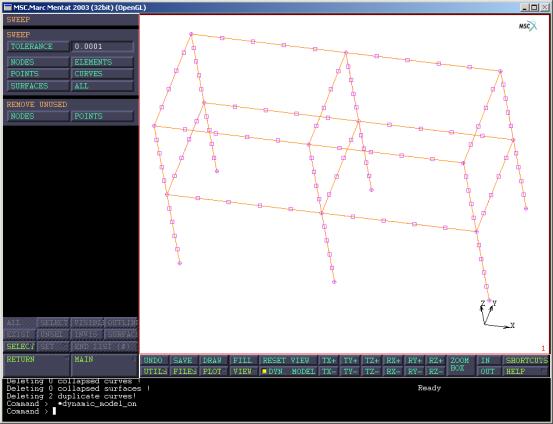
图
10 清理重复元素
(5)下面给模型输入材料信息。第一种材料为梁,需要说明的是,MARC的材料信息编号对应于截面编号,所以必须严格逐个输入。输入材料名称为Beam,材料类型为HYPOELASTIC->USER
SUB. UBEAM,即这个材料是用户自定义的。输入材料的密度为5000,即相当于将部分楼板重量折算到梁上面(图11)。
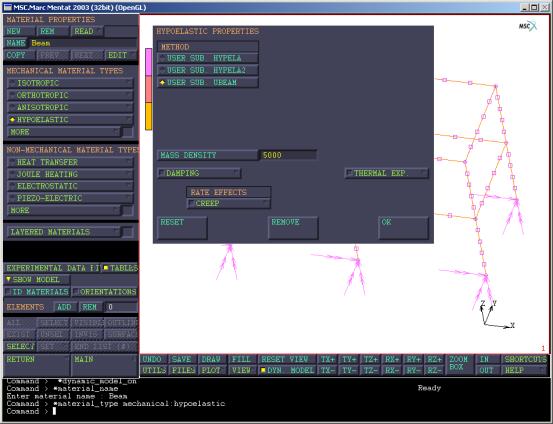
图11
定义梁材料信息
(6)选择ELEMENTS->ADD,选取相应的梁单元,将材料信息赋予之。
(7)再建立一个材料,名称为Column,类型还是HYPOELASTIC->USER
SUB. UBEAM,只是密度为2500。同样再选择ELEMENTS->ADD,选取相应的柱子单元,赋予材料信息。最后得到相应的材料信息如图12。
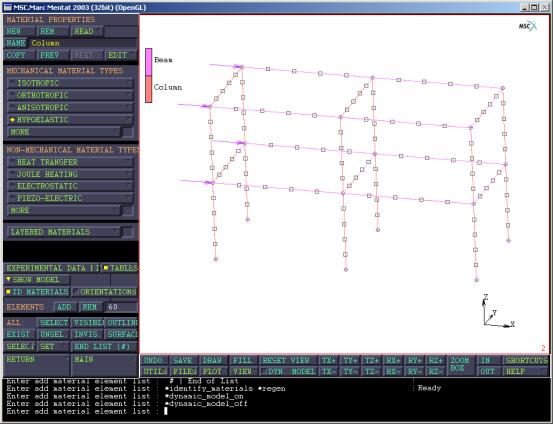
图12
定义柱子材料信息
(8)下面要赋予几何信息。这部分工作比较复杂,关键牵涉到单元局部坐标系的问题。选择主菜单MAIN MENU-> GEOMETRIC PROPERTIES,建立新几何信息名称为Beam,类型为3-D->ELASTIC
BEAM,输入截面的截面积和对应于局部坐标系x轴,局部坐标系y轴的转动惯量。并输入局部坐标系x轴对应整体坐标系的矢量方向。对于本问题而言,取梁单元的局部坐标系x轴为垂直向上,与整体坐标系的z轴平行,所以局部坐标系x轴的矢量方向为(0 0 1)(图13)。
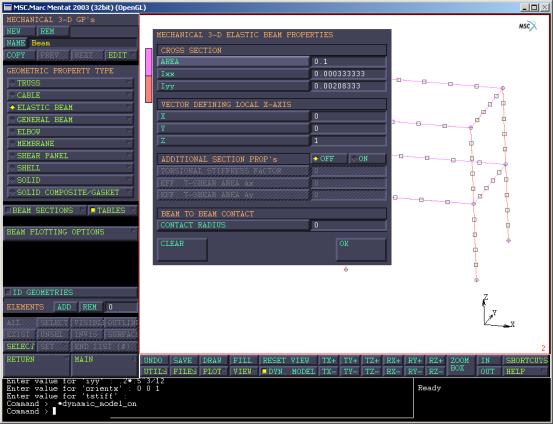
图13
定义梁截面几何信息
(9)将刚才输入的梁截面信息添加给所有的梁单元,选择ELEMENTS-> ADD,选取相应单元。
(10)类似的,建立新的几何信息,名称为Column,类型为3-D->ELASTIC BEAM,输入截面的几何信息如图14。这时取柱子的局部坐标系x轴方向和整体坐标系x轴方向相同,所以其局部坐标系x轴的矢量方向为(1 0 0),选择ELEMENTS-> ADD,将几何信息添加给相应的单元。
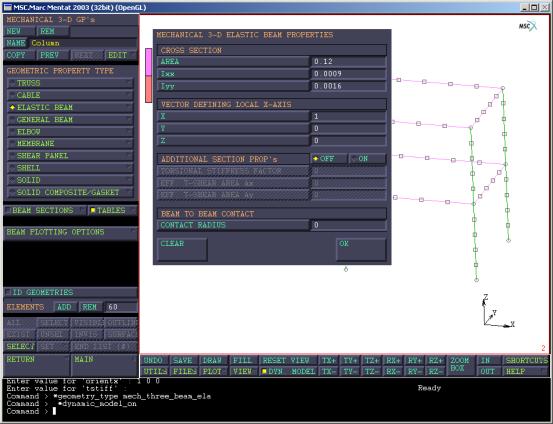
图14
定义柱子截面几何信息
(11) 其他包括输入荷载,定义工况等,与一般MSC.MARC相同。
(12) 最后编写matcode.txt文件,输入相应的截面塑性铰信息
Matcode.txt文件内容
|
内容
|
说明
|
|
2
|
第1行,定义一共有几个截面,这个模型里面一共有2个截面:1:梁。2:柱子
|
|
! 截面01,梁
3.00D+09,
1.00d+15,
1.00d+15,
5.00E+12,
3.49E+13,1.0e8,0.02,1000,0.8, -0.01, 1.05,1.0
3.99E+13
|
逐个输入截面信息,第1行,注释
第2行,N
第3行,Vx
第4行,Vy
第5行,Mx
第6行,My
第7行,T
|
|
! 截面02,柱
3.60E+09,
1.00d+15,
1.00d+15,
1.35E+13,
2.33E+13,1.6e8,0.10,50,0.2, -0.05, 1.05,1.0
3.58E+13
|
逐个输入截面信息,第1行,注释
第2行,N
第3行,Vx
第4行,Vy
第5行,Mx
第6行,My
第7行,T
|
主要参考文献和程序:
[1]
THUFIBER http://www.luxinzheng.net/research/THUFIBER.html
[2]
IDARC http://civil.eng.buffalo.edu/idarc2d50/
[3]
DRAIN-2D http://nisee.berkeley.edu/elibrary/getpkg?id=DRAIN2DX
[4]
Ibarra LF, Krawinkler H. (2006). Global Collapse of Frame Structures
under Seismic Excitations, PEER Report 2006/06, Page 29-42.
|