基于蛙跳格式显式积分算法改进OpenSees倒塌模拟
张书豪,田源等
算例模型和程序下载: OS_Explicit_Example.zip
OpenSees作为一款开源有限元计算软件,近些年被广泛的应用于大型工程结构的抗震性能研究和抗倒塌性能研究中。目前OpenSees的求解体系偏重于隐式算法,在显式算法方面只集成了最基本的中心差分法,当阻尼矩阵为非对角阵时该方法无法解耦方程组,计算时间大幅增加,实用性较差。
因此,本研究基于蛙跳法和中心差分法,建立了一种显式积分算法格式,并集成于OpenSees中。其后根据其稳定性条件,在OpenSees中集成了配合显式算法的振型阻尼模型。
一、显式积分算法的基本格式与稳定性条件
蛙跳法格式在半个时间步上得到速度,并利用速度计算下一时刻的位移,其基本过程如下:
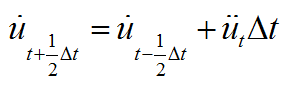 (1)
(1)
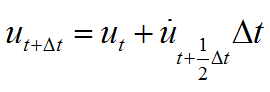 (2)
(2)
由式(1)与式(2)可知,蛙跳法是中心差分法的一种变异格式。在将其应用于结构动力分析时,需要联立运动方程求解,由于蛙跳法中速度和位移不在同一时间定义,故需要对运动方程进行修改:
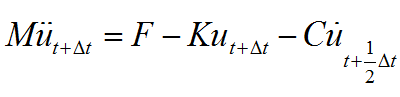 (3)
(3)
该方法相当于对速度项做单边差分,这种近似导致算法只有一阶精度,低于传统的中心差分法,但仍能满足一般工程计算的精度要求。
利用振型正交性可以将运动方程组解耦为一系列的振型方程,其后对每个振型方程推导其稳定性条件,可得到该方法的极限步长表达式为:
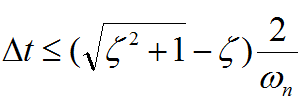 (4)
(4)
二、阻尼模型对显式算法的影响
由式(4)可知,显式算法的极限步长受到振型频率和振型阻尼比的影响。当采用经典的Rayleigh阻尼模型时,结构中的高阶振型阻尼比会被高估,此时算法极限步长将显著缩小。
从计算效率的角度考虑,可以只保留Rayleigh阻尼中的质量比例部分形成质量阻尼。质量阻尼形式简洁,但忽略了阻尼中的刚度成分,使得阻尼对某些参与度较高的次高阶振型以及高阶振型的抑制作用显著降低,某些情况甚至会导致结构产生显著的局部变形,使计算结果失真。
另一种方法,即采用振型阻尼模型,其形式如下:
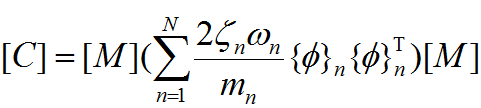 (5)
(5)
式(5)中变量N表示参与构造振型阻尼的数量,对于常规的建筑结构,取前10~50阶振型就能达到较为理想的精度。但振型阻尼模型只限制选中的振型,而其他振型阻尼比为0,因此可以将质量阻尼和振型阻尼结合使用(李志山 等,2015),综合效果更好。
算例 框架结构在地震荷载下的时程分析
利用一个框架算例来验证显式算法和阻尼模型的性能。如图1所示,该框架结构共8层,31.5m高,x轴方向3跨,y轴方向两跨,每跨5m。采用纤维模型模拟框架梁柱,该模型共包括1292个节点,1450个纤维梁柱单元。
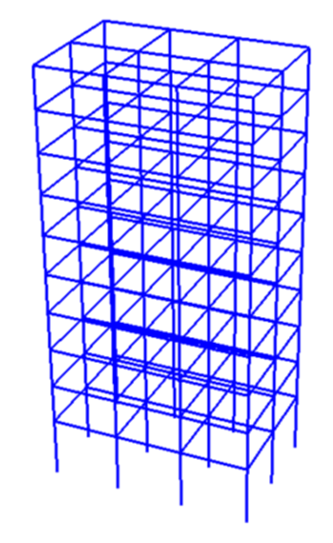
图1 某8层框架结构示意图
1. 大震弹性时程分析与弹塑性时程分析
选用El-Centro地震波,对该框架x方向施加地震动荷载,按照8度半的设防要求将地震波的峰值加速度取为510cm/s2。计算得到框架结构的顶层位移曲线如图2,图3所示。由图2可知,在弹性时程分析中三种工况计算得到的位移时程曲线趋势相同,峰值略有差别。其中,质量阻尼模型的位移峰值最高,其次为质量—振型阻尼模型(30阶振型参与),而采用Rayleigh阻尼模型得到的位移曲线峰值最小。
由图3可知,在弹塑性时程分析中, Rayleigh阻尼模型计算得到的位移曲线峰值最高,随后是质量阻尼模型,而质量+振型阻尼模型的位移峰值最小。这是因为结构进入塑性阶段后刚度出现软化,Rayleigh阻尼产生了变化;而质量阻尼、振型阻尼均不会随结构刚度变化而变化,阻尼矩阵与弹性时相同。
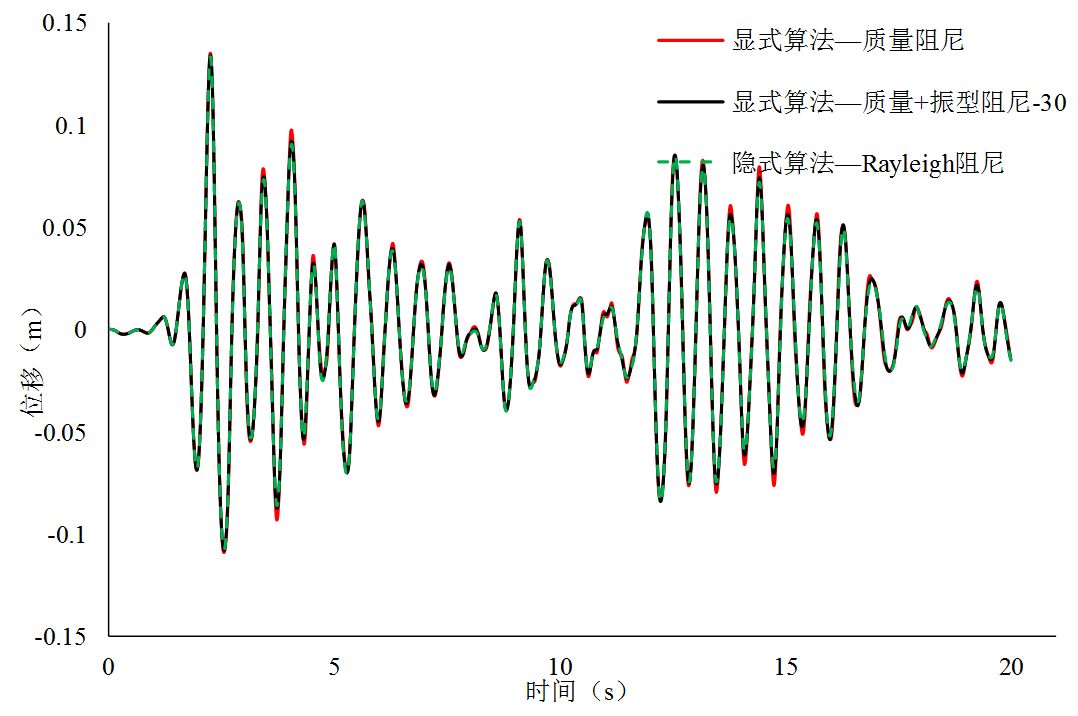
图2 框架弹性时程分析顶点位移时程曲线
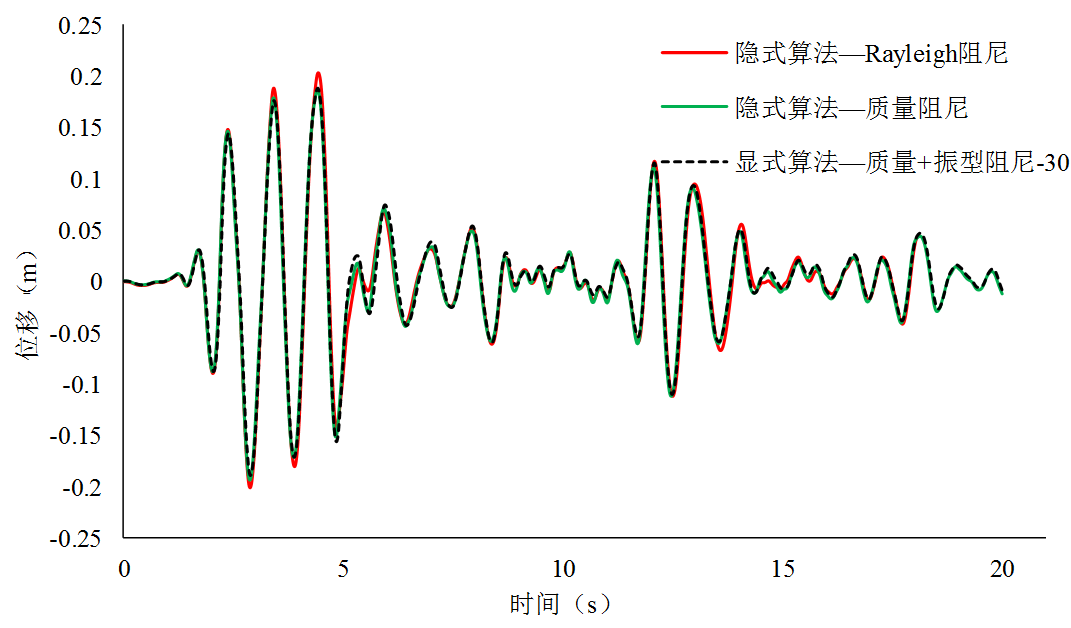
图3 框架弹塑性时程分析顶点位移时程曲线
2. 倒塌分析
仍采用El-Centro地震波,将峰值加速度调幅至3500cm/s2,进行时程分析。在大震时程分析中,模型中的钢筋利用steel02材料本构模拟,该材料本构曲线没有下降段。因此将steel02材料替换为Hysteretic材料,该材料可以模拟钢筋软化段,通过合理的参数标定可以模拟钢筋的断裂行为。
采用和大震时程分析相同的设置,隐式算法计算至2s左右就因收敛性问题中断,结果输出较短,故不再分析。而显式算法计算得到的顶层位移时程曲线如图4所示,底层位移曲线如图5所示,框架结构最终倒塌形式如图6所示。由图可知,利用显式算法计算时,采用不同阻尼模型的底层、顶层位移最终均呈现“一边倒”趋势,最终阶段底层位移甚至超过同一时刻的顶层位移,结构底层出现破坏。
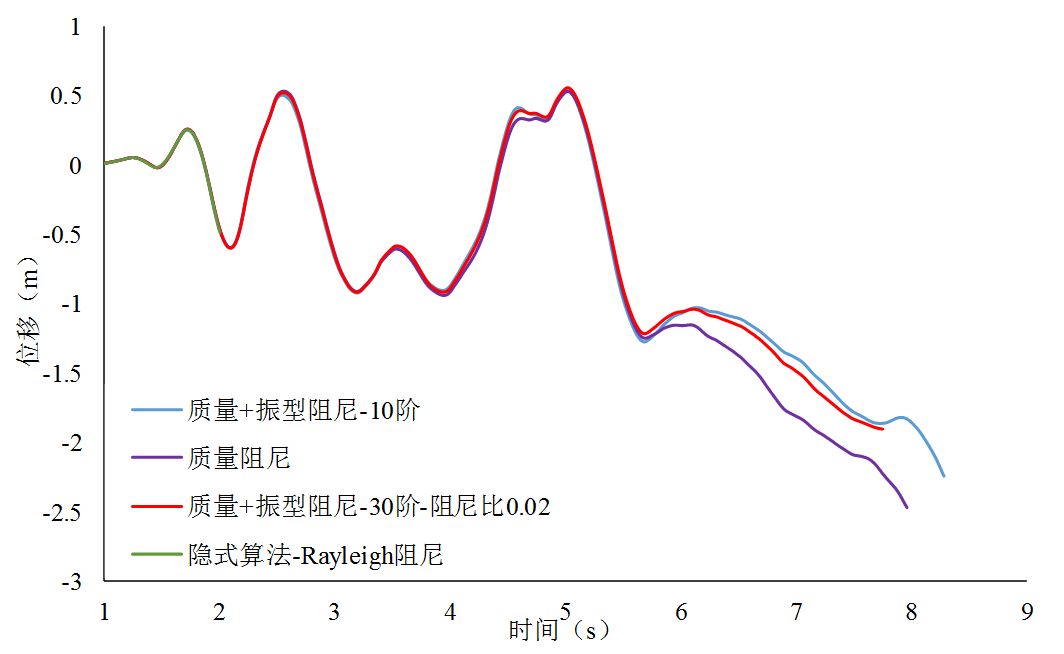
图4 框架顶层位移时程曲线
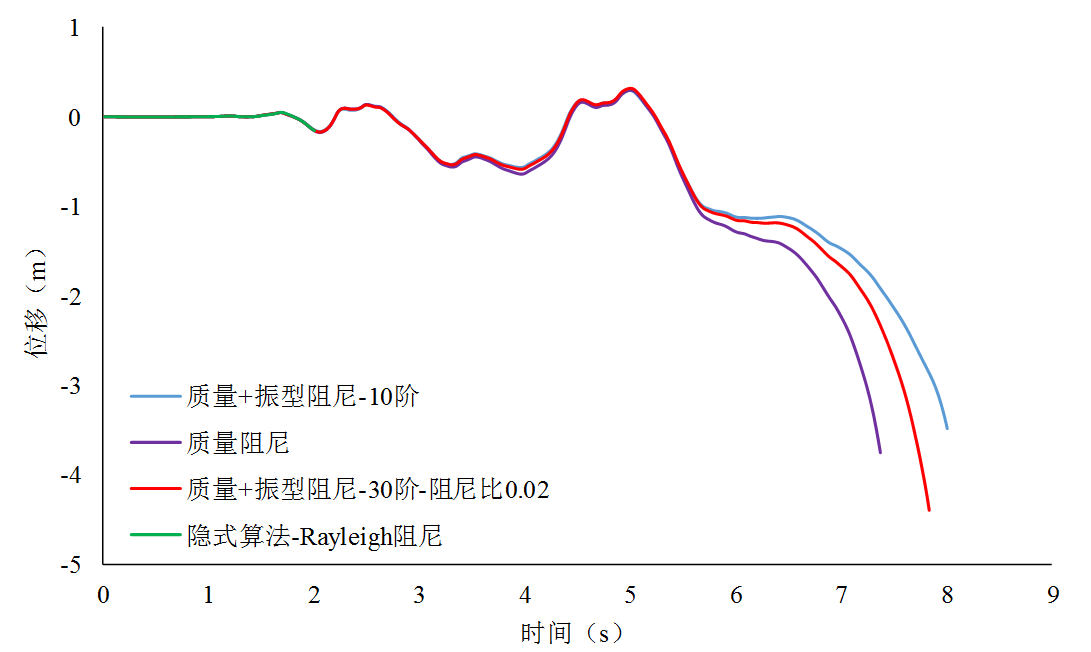
图5 框架底层位移时程曲线
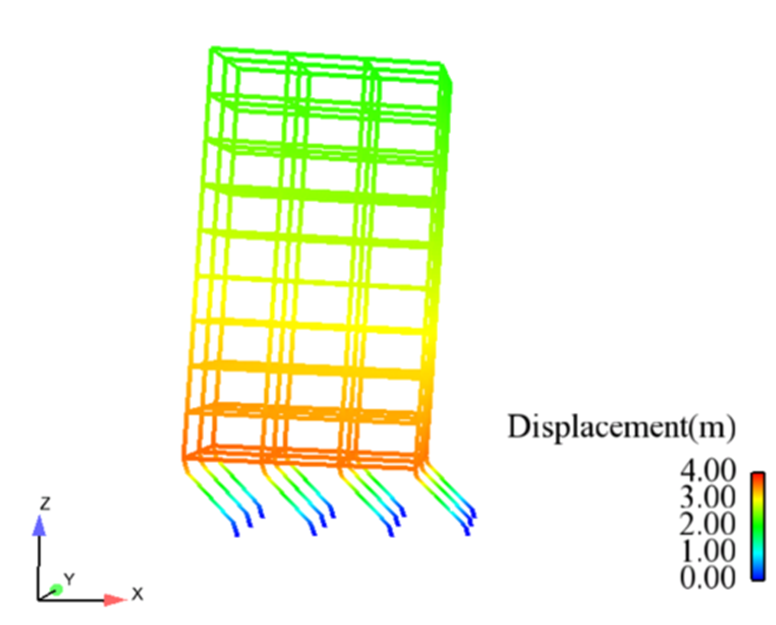
图6 框架的倒塌形式示意图
显式算法相关命令使用说明
1、 显式积分格式使用方法:
在模型中使用的显式算法严格来说是一种积分格式,在OpenSees中集成于Integrator类中。其使用命令为:
integrator Explicitdifference
使用该算法求解时,模型求解部分典型的命令流示例如下:
numberer RCM;
system Diagonal
algorithm Linear
integrator Explicitdifference
analysis Transient
analyze 400000 0.00005
其中,由于显式算法无需迭代求解,应将algorithm设置为Linear。此外,由于显式算法在求解时,方程的系数矩阵为质量矩阵,是一个对角矩阵,故应将system设置为Diagonal,此时算法效率最高。如果将system设置为其他选项,尽管方程解耦,但程序仍将按照常规线性方程组求解流程进行求解,可能会导致计算效率下降。
2、 振型阻尼使用方法:
由于OpenSees中并没有单独的类实现阻尼的功能,故在OpenSees中LinearSOE类和LinearSolver类下建立相应子类实现其功能。与LinearSOE对应的外部命令是system,故在使用振型阻尼时,应采用如下设置:
system DiagonalwithModelDamping
同时需要利用下列命令来设置振型阻尼的具体参数:
ModelDamping $Dratio $startfreq $endfreq $alphaM –getWholeDamping $nkernel
其中:
$Dratio: 振型阻尼的阻尼比。
$Startfreq: 起始频率,用来确定需要约束的频率范围
$endfreq: 终止频率,用来确定需要约束的频率范围。
$alphaM: 质量阻尼的比例系数,不与质量阻尼联合使用时设置为0。
-getWholeDamping:该命令让程序将完整的振型阻尼矩阵存储于内存中。
$nkernel: 计算振型阻尼力时使用的CPU核数,振型阻尼部分可以利用OpenMP架构进行并行化计算。
注意:由于振型阻尼需要结构的特征值和特征向量数据,故必须在求解命令前增加求解特征值的命令,且应该保证特征值的阶数足够。具体的示例见提供的模型文件。
最后给一个显式算法算的比较有特色的例子,是1:1的真实变形

图7 斜拉桥地震倒塌模拟(变形比例1:1)
说明:本研究仅为探索采用OpenSees进行倒塌模拟的研究同仁提供一种方法,算法还有很多问题,欢迎大家测试,完善。源程序待整理完成后会尽快提供给大家。
算例模型和程序下载: OS_Explicit_Example.zip
参考文献:
李志山,曹胜涛,刘春明,杨志勇. 2015. Rayleigh阻尼和振型阻尼在大规模建筑结构显式动力分析的实现及应用. 土木建筑工程信息技术, 7(6): 91-95.