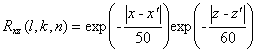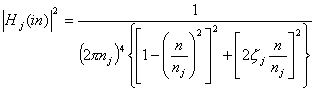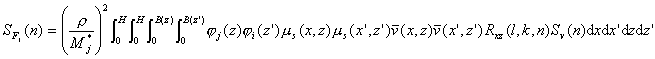空间索支撑幕墙结构风振计算方法及程序

1 概述

近年来，空间张拉结构，特别是空间索支撑幕墙结构的使用越来越广泛，由于幕墙结构自身的刚度较小，因此其风振效应往往显得格外重要。而幕墙结构的自身形状以及支撑情况又更加复杂，使得相当多的幕墙结构无法通过荷载规范提供的表格查得相应的风振荷载。因此，有必要从规范规定的风振荷载计算方法原理出发，编制相应的计算程序，以分析空间索支撑幕墙结构的风振荷载。

2 基本原理

由维纳－辛钦关系，第j振型和第i振型广义力互谱密度 由其互相关函数 得到：

对于第i阶振型，其广义风荷载的表达式 为

式中 为振型， 为脉动风压，

为广义质量

整理得

式中，

为脉动风相干函数平方根，我国规范建议取为如下形式

为风功率谱，我国规范取为Davenport谱

对于阻尼比小且自振频率稀疏时，忽略交叉项，则位移响应谱密度 为

式中，

则位移响应的根方差为

考虑安全度g，设计动位移为

我国规范建议g取为2.2

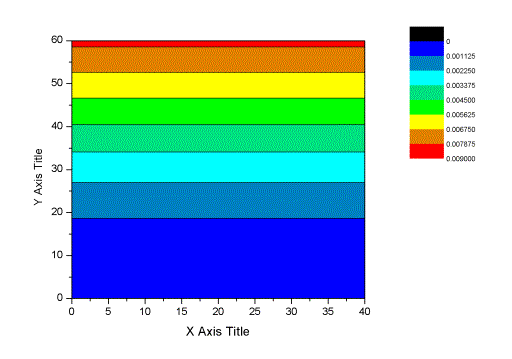
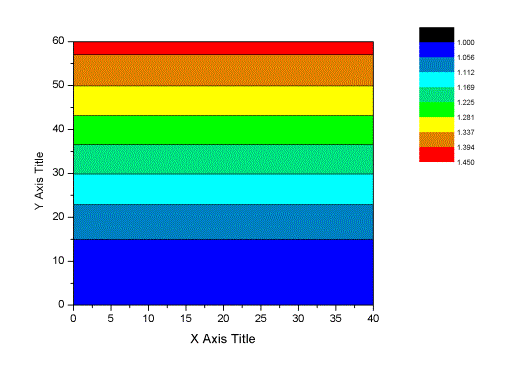
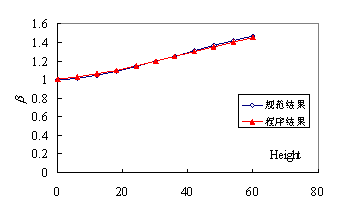
3 计算程序

根据上述公式编制计算程序，程序用户需要输入：

a)       风场环境 A~D类

b)      基本风压对应的风速v₁₀

c)      结构自振频率，单位Hz

d)      结构自振振型

e)       结构的阻尼比

f)       输入相应振型输入点对应的风载体形系数

4 程序验证及结果讨论

4.1 程序验证

取一空间悬臂板，高度为XXm，宽度为XXm，设定其自振频率为2.5Hz，B类风场，v₁₀=XX.Xm/s，阻尼比为0.01。其一阶振型对应的振型位移如图4.1.1所示。

图4.1.1 一阶振型

程序计算得到其一阶自振对应的风振系数b分布如图4.1.2所示

图4.1.2 一阶振型对应的风振系数b分布

由于该板比较规则，可以依据规范得到其风振系数延高度的分布，与程序计算结果对比如图4.1.3所示，可见二者非常接近，最大误差不超过2.5%

图4.1.3 风振系数对比（自振频率2.5Hz，阻尼比0.01）

将阻尼比增加到0.05，与规范对比结果如图4.1.4所示。可见阻尼比增加，结构的风振系数减小，程序计算结果和规范吻合良好。

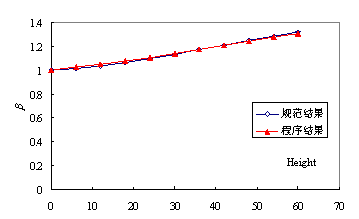
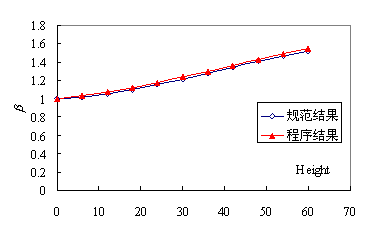
图4.1.4 风振系数对比（自振频率2.5Hz，阻尼比0.01）

将结构的自振频率降低到1.5Hz，阻尼比仍为0.1，程序计算结果和规范结果对比如图4.5所示。可见随着频率降低，结构风振系数增加，程序计算结果和规范吻合良好。

图4.1.5 风振系数对比（自振频率1.5Hz，阻尼比0.05）

从上述对比可以看出，本文建议模型和规范建议结果吻合良好。可以用该程序分析某些规范中未曾规定的结构风振效应。

4.2 索支撑幕墙结构

4.2.1 计算模型

一索支撑幕墙结构如图4.2.1所示，幕墙高度为XXm，宽度为XXm，厚度为XXm，周边固定。支撑索直径Xcm，初始张拉应力XXXMPa。幕墙结构面密度为XXkg/m²。

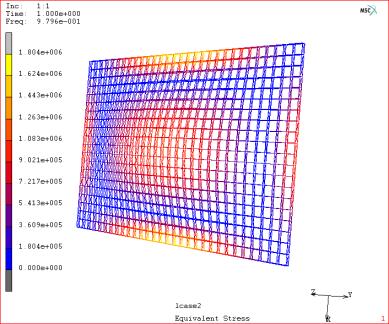
图4.2.1 索支撑幕墙

4.2.2 结构自振振型

计算得到结构的前三阶周期为0.9796Hz，1.362Hz，1.906Hz。相应的振型如图4.2.2~4所示。

图4.2.2 一阶振型

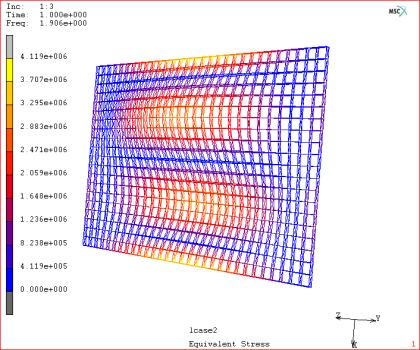
图4.2.3 二阶振型

图4.2.4 三阶振型

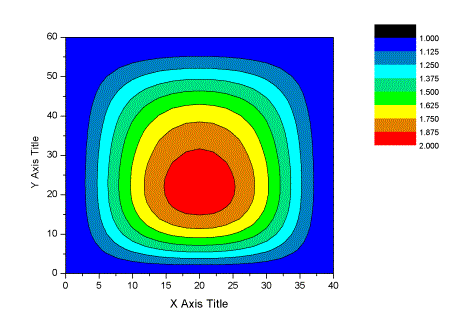
4.2.3 结构风振系数分布

将上述振型数据输入风振系数计算程序，如果取场地为B类，程序计算结果界面如图4.2.5所示。计算得到的一阶风振系数分布如图4.2.6所示。由于该结构比较复杂，为了安全期间，考虑了前三阶振型，结果发现，如果只考虑一阶振型，最大风振系数为1.709，考虑前两阶振型，最大风振系数为1.722，考虑前三阶振型最大风振系数仍然为1.722，说明考虑前三阶振型精度已经足够。最后计算得到的结构风振系数分布如图4.2.7所示，最大风振系数为1.72。

如果取场地为C类场地，则前三阶振型组合后得到的风振系数分布如图4.2.8所示，最大风振系数为1.96。风振系数变化的主要原因是由于风压高度变化系数差异引起的。

图4.2.5 程序输出界面

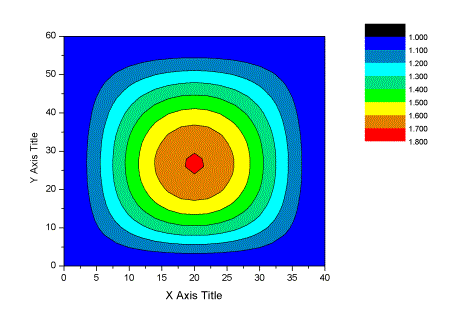
图4.2.6 一阶振型对应的风振系数分布（B类场地）

图4.2.7 前三阶振型组合得到的风振系数分布（B类场地）

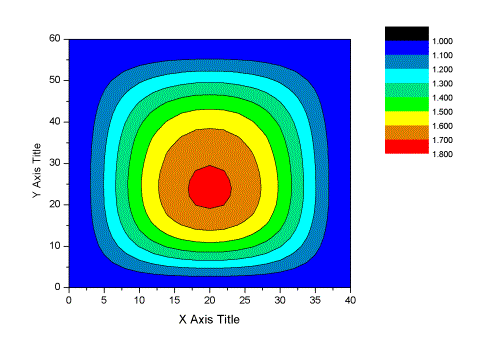
图4.2.8前三阶振型组合得到的风振系数分布（C类场地）