Proc. Third International Conference on FRP Composites in Civil Engineering (CICE 2006) , December 13-15 2006, Miami, Florida, USA, pp: 391-394.

Numerical modeling of FRP shear strengthened

RC beams using compression field theory

Zhe Qu

(Postgraduate, Tsinghua University, Beijing, China)

Xin-Zheng Lu

(Lecturer, Tsinghua University, Beijing, China)

Lie-Ping Ye

(Professor, Tsinghua University, Beijing ,China)

Jian-Fei Chen

(Lecturer, Edinburgh University, Edinburgh, UK)

John Michael Rotter

(Professor, Edinburgh University, Edinburgh, UK)

Download PDF version

Abstract

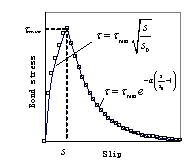
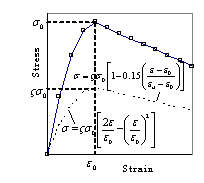
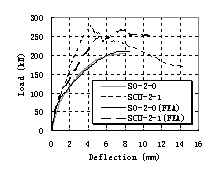
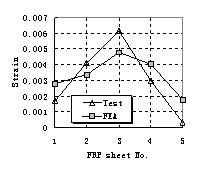
The modified compression field theory and an advanced bond-slip model are implemented in a general finite element analysis package to evaluate the shear behaviour of FRP strengthened reinforced concrete beams. The inclination angle of the critical shear crack is estimated and the debonding phenomenon is simulated. A close agreement is achieved between the predicted average FRP strains and those in a test beam reported in the literature. Further research is being conducted to simulate behaviour of FRP shear the interaction between the external FRP shear reinforcement and concrete.

KEYWORDS

Shear, FRP, strengthening, concrete, modified compression field theory (MCFT)

1. Introduction

The modified compression field theory (MCFT) has been an alternative method for shear design of reinforced concrete members since late 1980s when it was established by Vecchio and Collins (1986). It takes into account the three basic principles of mechanics and is able to calculate the inclination of the diagonal shear crack, which is essential in predicting the shear behaviour of reinforced concrete beams.

With the increasing interest in the technique of strengthening RC members with externally bonded FRP for shear, a number of studies have been carried out to include the contribution of FRP in the MCFT in the last few years. Malek and Saadatmanesh (1998) extended MCFT to include the contribution of FRP sheets with variable concrete crack angles. However, they assumed a uniform distribution of FRP strain throughout the depth of the beam and no slip between the FRP and concrete was taken into account.  Lees et al. (2002) analysed the development of strain in FRP sheets using MCFT based on similar assumptions. Wong et al. (2003) considered the bond-slip behaviour of FRP-concrete interface in the MCFT model by introducing elastic or perfectly elasto-plastic link elements. They concluded that it is necessary and viable to model the interface behaviour between FRP and concrete but a more advanced bond-slip constitutive model must be adopted.  

In this paper, the MCFT is implemented in the finite element software MSC. MARC (2003) to simulate the shear behaviour of FRP strengthened concrete beams. An advanced bond-slip relationship is adopted to model the FRP-concrete interface. Numerical predictions are compared with test results from the literature. 

2. The Model

The MCFT adopts a smeared crack model. The bond behaviour between the FRP and the concrete plays a crucial role and debonding of FRP from concrete almost always happens prior to the final shear failure of a concrete beam shear strengthened with FRP (Chen and Teng 2003). However, this interfacial bond-slip behaviour cannot be directly incorporated into the MCFT model when the FRP starts to debond. In this study, the reinforced concrete is modelled using a constitutive model based on the MCFT. The FRP strips are modelled separately and linked to the concrete surface by using nonlinear springs based on Lu et al.¡¯s (2005) bond-slip relationship (Fig. 1a).

In the MCFT, the reinforced concrete is treated as a continuous material with the reinforcements and cracks smeared in the elements. The rotating-angle crack model is commonly used. The in-plane constitutive model in the MCFT is established based on the uniaxial constitutive models for concrete and steel reinforcement. The widely-used uniaxial stress-strain relationship for concrete proposed by Hognestad (1952) and that for steel reinforcements (Fig. 1b) suggested by T. T. C. Hsu and his colleagues (Belarbi and Hsu 1995) are adopted in this study. To introduce the compression softening effect of concrete, Hognestad¡¯s model is modified here by including a softening coefficient z which was proposed by Belarbi and Hsu (1995). The concrete compressive stress (s) strain (e) relationship (Fig. 1c) is thus given as

                                                                                                                                (1a)

                                                                                                             (1b)

                                                                                                                                              (1c)

where s ₀ is taken as the concrete cylinder compressive strength, e₀ and e_u are the peak and ultimate compressive strains respectively, and e₁ is the current principal tensile strain in the concrete.

(a) FRP-concrete bond-slip                            (b) Steel bar                                         (c) Concrete in compression

Figure 1:  Uniaxial stress-strain relationships

To take into account the effect of the complex stress state of concrete underneath the FRP strips on the FRP-concrete bond-slip behaviour, the biaxial strength model for concrete proposed by Kupfer (1969) is introduced into the FE model to modify the concrete tensile strength:

                                                                                                                                           (2)

where s₂ is the principal compressive stress in the concrete, and f_c and f_t are the uniaxial compressive and tensile strengths of concrete respectively.

A procedure for determining the stress state from a given strain state and strain increment was derived within the framework of MCFT, which makes use of compatibility and equilibrium conditions and the above constitutive relationships. The procedure was implemented in MARC through the user subroutine HYPELA2.

3. Numerical predictions and comparison with test results

RC beam SCU-2-1 shear-strengthened with CFRP U-jackets and its corresponding un-strengthened control beam S0-2-0 as reported in Tan and Ye (2003) were investigated using the aforementioned FE model. Both beams had a shear span-to-depth ratio of 2.155 and were tested under 4-point-bending. The beams had a depth of 260mm and material properties as listed in Table 1. The concrete cylindrical compressive strength f_c was taken to be 0.8f_cu.

Table 1: Material properties of specimens

Figure 2: Finite element model for specimen S-CU-2-1

Due to symmetry, only a half span of the beams was modelled (Figure 2). The RC beams were modelled using the user-defined 2D RC material model based on MCFT and the FRP strips were modelled as an orthotropic material. The nodes of the FRP elements were linked to the nodes of the RC element by user-defined nonlinear spring elements with appropriate properties of the adopted bond-slip model. The lowest row of the FRP nodes was rigidly linked to the bottom of the beam because no slip was possible between the beam and the FRP U jackets there. 

Figure 3 shows a comparison of the distribution of the predicted principal tensile strain with the test diagonal crack pattern. It is seen that the predicted inclination angle is very close to the test crack angle. Figure 4 shows the simulated failure process where the FRP strain value is proportional to the darkness of the colour. In the test, FRP strip No. 4 was debonded first, followed by the debonding of strip No.3 and then No. 2. The beam eventually failed due to the debonding of FRP strip No. 1. This failure process is closely reproduced as in Figure 4.

The predicted load-deflection curve for the un-strengthened beam specimen S0-2-0 is in good agreement with the test results (Fig. 5), but that for the FRP strengthened specimen SCU-2-1 has some deviation from the test curve. The main cause for this disparity may be the inability of the present FE model to simulate factors such as the enhanced dowel action by the presence of the FRP. Figure 6 shows that the average tensile strain in the FRP strips along the diagonal crack is close to the test value, but the predicted strain distribution is more uniform compared with the test results which may be attributed to the adoption of the smeared crack model.

(a) Predicted principal tensile strain distribution                    (b) Crack pattern in the test beam

Figure 3: Predicted principal tensile strain versus test crack pattern when the middle FRP strip debonded

Figure 4: Development of axial strain distribution in FRP strips

4. Conclusions

This paper has presented a study on the shear behaviour of FRP strengthened RC beams. The modified compression field theory is built into a general-purpose finite element analysis software package. The bond-slip relationship of FRP-concrete interface is modified by reducing the concrete tensile strength according to the biaxial stress state of concrete underneath the FRP strips. The results show that the model is capable of predicting the inclination angle of critical shear crack as well as the debonding procedure of FRP strips, which are both essential in predicting the shear capacity of FRP strengthened RC beams. 

5. Acknowledgements

The authors would like to acknowledge the financial support provided by the Royal Society through the Royal Society-NSFC UK-China Joint Project (Grant No. IS 16657) and the National Natural Science Foundation of China through a key project for FRP in construction (Project No. 50238030).

6. References

Belarbi, A. and Hsu, T.T.C. (1995). ¡°Constitutive laws of softened concrete in biaxial tension-compression¡±. ACI Structure Journal, Vol. 92, No. 5, pp562-573.

Chen, J.F. and Teng, J.G. (2003). ¡°Shear capacity of FRP strengthened RC beams: FRP debonding¡±. Construction and Building Materials, Vol.17, No.1, pp27 ¨C 41.

Hognestad, Eivind (1952). ¡°Inelastic behaviour in tests of eccentrically loaded short reinforced concrete columns¡±. ACI Journal, Vol. 49, No. 10, pp117-139.

Kupfer, H., Hilsdorf, H. K., Rush H. (1969). ¡°Behavior of concrete under biaxial stresses¡±. ACI Journal, Vol. 66, No. 8, pp656-666

Lu, X.Z., Teng, J.G., Ye, L.P. and Jiang, J.J. (2005). ¡°Bond-slip models for FRP sheets/plates externally bonded to concrete¡±. Engineering Structures. Vol. 27, No. 6, pp938-950.

Lees, J.M., Winistorfer, A.U., Meier, U. (2002) ¡°External prestressed carbon fiber-reinforced polymer straps for shear enhancement of concrete.¡± Journal of Composites for Construction, Vol. 6, No. 4, pp249-256.

Malek, A.M., Saadatmanesh, H. (1998). ¡°Ultimate shear capacity of reinforced concrete beams strengthened with web-bonded fiber-reinforced plastic plates.¡± ACI Structure Journal, Vol. 95, No. 4, p391-399.

Tan, Z. and Ye, L.P. (2003) ¡°Experimental research on shear capacity of RC beam strengthened with externally bonded FRP sheets¡±. China Civil Engineering Journal, Vol. 36, No. 11, pp12-18

Vecchio, F.J. and Collins, M.P. (1986). ¡°The modified compression-field theory for reinforced concrete elements subjected to shear¡±. ACI Journal, Vol. 83, No. 2, pp219-231.

Wong, Rita S.Y. and Frank J. Vecchio. (2003). ¡°Towards modeling of reinforced concrete members with externally bonded fiber-reinforced polymer composites." ACI Structure Journal Vol. 100, No. 1, pp 47-55.