"CFRP索流固耦合风振研究"--第十二届全国结构风工程学术会议论文集, 西安, 2005, 69-75.

CFRP索流固耦合风振研究

第十二届全国结构风工程学术会议论文集, 西安, 2005, 69-75.

摘要：碳纤维增强复合材料（CFRP）由于轻质高强，在大跨领域有着很好的应用前景。CFRP索材由于重量很轻，其风振行为需要给予更多关注。本文利用通用有限元软件ANSYS提供的流固耦合分析功能，对CFRP索的风振行为进行了研究，讨论了不同的湍流模型，以及CFRP索在均匀风场和脉动风场下的风振行为。分析结果表明，CFRP索由于质量很轻，气弹阻尼效果明显，如果设计合理，其风振作用可能会优于同尺寸钢索。

关键词：CFRP索，大跨，风振，流固耦合

中图分类号：TU328 文献表示码：A

Study on the Fluid-Solid Coupled Wind-induced Vibration of CFRP Cable

Lu Xin-zheng, Ye Lie-ping, Ma Qian-li, Jiang Jianjing

Department of Civil Engineering, Tsinghua University, Beijing, 100084

Abstract: Due to the lightweight and high strength of Carbon Fiber Reinforced Polymer (CFRP), it has good application future in large span structures. Since the self-weight of CFRP cable is very light, more study should be given on its wind-induced vibration. In this paper, the wind-induced vibration of CFRP cable is studied with the fluid-solid coupled simulation function of ANSYS, a common finite element package. Different turbulence models are discussed. And the responses of CFRP cable in stable and fluctuant wind fields are simulated. The numerical results show that due to the lightweight of CFRP cable, the aerodynamic damping effect is more obvious. So with proper design, the wind-induced vibration of CFRP cables may have better performance than steel cables with the same size.

Keyword: CFRP cable, large span, wind-induced vibration, fluid-solid coupled

基金项目：国家自然科学香港、澳门青年学者合作研究基金（项目编号：50329802）与国家自然科学重点基金（项目编号：50238030）

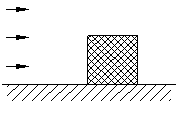
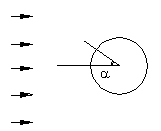
1 引言

碳纤维增强复合材料（Carbon Fiber Reinforced Polymer，简称CFRP）由于具有轻质、高强、耐腐蚀等诸多优点，因而在大跨结构领域有着广阔的应用前景^[1-3]。而用CFRP索代替钢索用于索支撑结构，是目前CFRP在大跨领域应用中一个比较可行的方案。然而，由于索材质量很轻，侧向刚度较小，因此由风引起的风振效应不可忽略。国内外已经发生过多起钢索由于风振而导致严重损伤甚至破坏的事故。由于CFRP比钢索的质量还要轻，可能应用的跨度会更大，因此其风致振动问题需要进行专门研究。

尽管目前基于风洞实验及随机振动理论，结构风工程已经得到了长足的发展。但是，由于建筑结构体形很大，风洞实验尺寸效应问题突出，且如果牵涉到结构和空气流场的耦合振动问题，则实验模型相似比设计将变得更为复杂，且风洞实验的代价也较高。因此，基于现代计算流体动力学（Computational Fluid Dynamics，简称CFD）和计算固体动力学（Computational Structural Dynamics，简称CSD）的流固耦合数值仿真有着很好的应用前景^[4,5]。

由于硬件计算能力和软件计算模型的限制，目前对结构的流固耦合数值分析大部分还是二维的研究^[4]。计算机和软件技术的发展使得全三维的流固耦合数值模拟成为可能，本文基于通用有限元软件ANSYS，对CFRP索的风致振动进行了三维流固耦合数值仿真，对计算中的相关参数进行了细致讨论，并和钢索的风致振动进行了对比。

2 ANSYS的流固耦合计算功能

2.1 计算方案

一般流固耦合问题中，包含了三个不同的分析模块^[4]：

(1) 流体域（CFD）：由于风速一般比较低，可以将空气看作不可压缩流体；

(2) 结构域（CSD）：由于结构一般不允许在风荷载下屈服，因此结构一般为考虑大位移带来的几何非线性的固体；

(3) 流体－固体界面：由于流体计算一般基于欧拉网格描述，而固体计算一般基于拉格朗日网格描述，因而流体和固体之间的界面是流固耦合分析的一个关键问题。目前比较成熟的分析方法是任意拉格朗日网格法（Arbitrary Lagrangian-Eulerian，简称ALE）。

计算的流程一般为：

(1) 以未变形的结构作为流体的计算边界，计算流体流场，得到作用在结构表面的压力；

(2) 将该压力作用于结构，使结构产生变形，进而根据结构的变形修改流体边界及流体网格，重新进行流体计算分析；

(3) 重复迭代步骤(1)和(2)直到流体和固体界面两次计算的压力差小于误差容限。

由于结构域（CSD）计算目前已经非常成熟，且土木结构即使是大位移往往变形也有限，在有合适的网格划分技术的情况下，界面网格调整相对也并不复杂，因此流固耦合计算的精度和难点主要表现在对于土木结构这样的钝体外形，如何能够准确计算其周边流场及压力场。

2.2 流体分析模型

在ANSYS中，提供的流体分析模型为雷诺平均法^[5,6]。其核心是不直接求解瞬时Navier-Stokes方程，而是求解平均化的雷诺方程。这样可以有效减少计算量，因而得到了大量的工程应用，也相对比较成熟。

雷诺平均法由于需要对瞬时湍流进行平均化处理，因此如何构建合适的平均化的湍流模型是该方法的关键问题，ANSYS程序中提供了7种不同的湍流模型，分别是：

(1) Standard k-e model （本文简称SKE模型）

(2) Re-Normalized Group Turbulence model（简称RNG模型）

(3) k-ε Model due to Shih （简称NKE模型）

(4) Nonlinear Model of Girimaji （简称GIR模型）

(5) Shih, Zhu, Lumley Model （简称SZL模型）

(6) k-ω Turbulence Model（本文简称SKW模型）

(7) Shear Stress Transport Turbulence Model (本文简称SST模型)

已有研究表明，对于同样的问题，采用不同的湍流模型可能得到差异悬殊的结果^[5]。尤其是对于土木结构这样的钝体，差距可能更大。Standard k-e模型已经被大量研究证明在分析钝体流场时是不合适的^[4,5,7]，而近年来计算风工程中采用得比较多的是RNG模型^[8]。因此，为了对上述模型有一个全面的认识，本文首先对不同湍流模型的计算结果进行了对比分析。

对比计算包含以下三个不同的基本分析对象：

(a) 正方形房屋的风压分布，如图1(a)所示；

(b) 正方形柱体绕流流速分布，如图1(b)所示；

(a) 正方形房屋风压分布 (b) 正方形柱体绕流 (c) 圆柱体绕流

(a) Wind Pressure on the square building (b) Wind pass a square cylinder (c) Wind pass a round cylinder

图1 流场基本分析对象

Fig. 1 Fundamental objects in fluid analysis

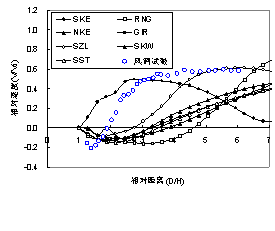
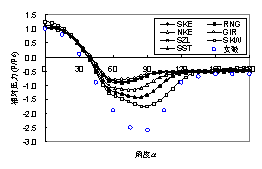
2.3 基本模型结果讨论

各工况分析结果简要介绍如下：

(a) 对于正方形房屋的风压分布，已有研究表明^[5,7,9]，Standard k-e 模型会过高估计迎风面檐口的风压，其他模型均在此基础上有所改进，不同计算模型得到的风压分布如图2所示（实验资料来源：文献[7]）。可见，数值计算结果和风洞实验结果总体上吻合较好，但是在迎风面檐口差异较大，相对而言，RNG、GIR、SZL、SKW模型结果较好，SKE模型结果较差。

(b) 对于正方形柱体绕流流速分布，计算结果和实验结果对比如图3所示（实验资料来源：文献[10]）。从对比中可以看出，由于钝体绕流分析，目前各湍流模型分析都有较大难度，相对而言，SZL模型和GIR模型和实验结果更为接近一些，而其他模型差距更大。

(d) 对于圆柱体绕流流场分析，计算结果和实验结果对比如图4所示（实验资料来源：文献[5]）。从对比中可以看出，正风向各模型和实验结果基本一致，横风向SST、SKW和SKE模型和实验结果较为接近，其他模型在计算结果偏小。如果比较不同模型的流速云图，可以发现，RNG模型、GIR模型和SZL模型（图5）的计算结果和实验结果比较相似，而其他模型计算结果则差异较大。

图2 房屋表面风压分布对比

Fig. 2 Comparison for wind pressure on the building

图3 正方形柱体后部流速分布对比

Fig.3 Comparison for wind speed along the centerline of square cylinder

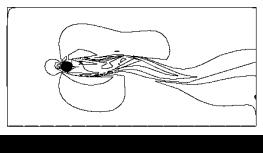
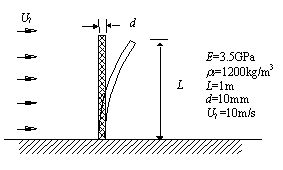
图4 圆柱体表面风压对比图5 SZL模型流速分布图

Fig. 4 Wind pressure on the round cylinder Fig. 5 Wind speed distribution with SZL model

为了进一步论证不同湍流模型在耦合分析中的差异，需要进行考虑流固耦合效应的模型对比分析。因为目前还很难找到考虑流固耦合效果的标准实验，因此本文以文献[11]中提供的带隔板的二维流场问题作为对象进行了对比分析（图6）。不同湍流模型分析结果和文献[11]中结果的差异如图7所示。其中，GIR模型由于计算结果发散，未能得到其振动频率。从对比中可以看出，RNG和SZL模型的计算结果和文献[11]中结果最为接近。

图 6 带隔板二维流场问题

Fig. 6 2D flow problem with an isolate plate

图7 不同湍流模型结果与文献[11]误差对比

Fig. 7. Comparison for errors between different models with Ref [11]

综合上述对比分析，各模型计算效果对比如表1所示。

表1 不同湍流模型计算结果对比

Table 1 Comparison for the results with different turbulent models

	SKE	RNG	NKE	GIR	SZL	SKW	SST
正方形房屋风压分布	×	☆	△	☆	☆	☆	△
正方形柱体绕流	×	×	×	△	☆	×	×
圆柱体绕流（压力分布）	☆	×	△	×	×	☆	☆
圆柱体绕流（流场分布）	×	☆	×	☆	☆	×	×
带隔板流固耦合	☆	☆	×	×	☆	×	△

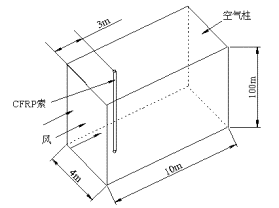
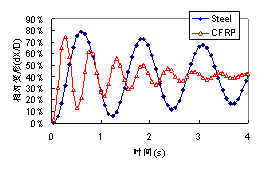
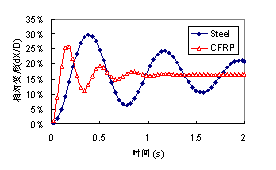
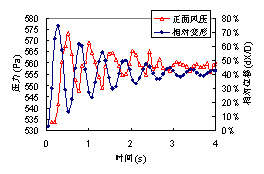
符号说明：☆：较好；△：一般；×：较差

从表中可以看出，对于本文研究的CFRP索流固耦合振动问题而言，RNG模型和SZL模型相对比较合适，而其他模型的问题相对要大一些，该结论也和一些理论分析相一致。

3 CFRP索风振计算

3.1计算模型

取CFRP索长度为100m，直径为10cm，弹性模量为230GPa，密度为1400kg/m³。设定索内初始应力为200MPa或500MPa。为了考虑CFRP索和周围空气的流固耦合作用，在索周围取4m×10m×100m的立方体空气柱。整个计算模型如图8所示。

(a) 模型尺寸 (b) 有限元网格（局部）

图8 CFRP索风振计算模型

Fig. 8 Computational model for the wind-induced vibration of CFRP cable.

分别进行了一个平稳风场工况和三个脉动风场工况的计算，平均风速均为30m/s，并和钢索进行了对比。

3.2 平稳风场计算结果

当初始张拉应力分别为200MPa和500MPa时，分别采用RNG模型和SZL模型，对CFRP索和钢索的流固耦合风振进行了分析。分析发现RNG模型和SZL模型计算结果非常接近，以SZL模型计算结果为例，CFRP索和钢索在平稳风场作用下最大变形的时程如图9所示。从图中可以得到以下结论：

(1) 周围空气对索的气弹阻尼效果非常明显，虽然计算模型中未设置任何阻尼，但是由于索周面空气的影响，无论是钢索还是CFRP索的振动都表现出明显的随时间衰减。以CFRP索为例，将CFRP索迎风面（正面风压）和索的振动时程放在一起，如图10所示，就可以明显看出，周围空气流场对CFRP索振动有一个明显的反向抑制作用。并且，索的振幅越大、振动频率越快，周围空气流场的抑制作用也就越明显。考虑周围空气的气弹阻尼作用，从图9索的振动中可以估算出：对于CFRP索，当初始应力为200MPa时，阻尼比大约为0.053，而当初始应力为500MPa时，由于索振动频率更快，气弹阻尼也就更大，阻尼比达到了约0.11。对于钢索也有类似现象。当初始应力为200MPa时，钢索阻尼比约为0.015，而初始应力为500MPa时，阻尼比达到了0.067。

(2) 数值计算得到的索的一阶振动频率和理论频率对比如表2所示，从表中可以看出，计算频率均小于理论频率值，说明考虑流固耦合作用后，周围空气和索一起振动，气弹质量降低了索的振动频率。且由于CFRP索更轻，周围空气质量影响也就更大，相应的数值计算得到的频率和理论值的差异也就更大一些。但是总的说来，无论是钢索还是CFRP索，频率和理论值的差别都小于5%，说明对于索的振动而言，气弹质量和气弹刚度的影响相对比较小。

(3) 在本次分析中，索主要为顺风向振动，横风向的振动始终很小，本文认为，这主要是由于目前的湍流模型对侧风向的风压计算精度不高所致（图4）。

(a) 初始应力=200MPa (b) 初始应力=500MPa

图9 平稳风场作用下索最大相对变形时程曲线（dX为索最大变形，D为索直径）

Fig. 9 The time-history curves of maximal relative deformation of cables in stable wind field

(a) 初始应力=200MPa (b) 初始应力=500MPa

图10 CFRP索迎风面（正面风压）及变形时程曲线

Fig. 10 The time-history curves of wind pressure and deformation of CFRP cables

表2 索的一阶自振频率

Table 2 Free vibration frequencies of cables (First model)

	数值计算		理论频率（不考虑阻尼）		理论频率（考虑阻尼）
	CFRP索	钢索	CFRP索	钢索	CFRP索	钢索
200MPa	1.810	0.779	1.890	0.801	1.887	0.800
500MPa	2.807	1.233	2.99	1.266	2.97	1.266

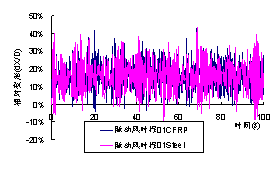
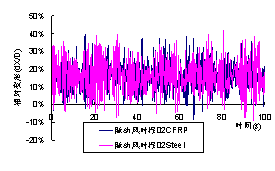
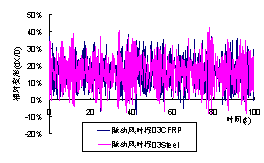
注：L为索长度，T为索拉力，M为索单位长度质量， x为阻尼比

3.3 脉动风场计算结果

采用谐波合成法（WAWS），根据Davenport谱，生成了3条随机脉动风时程，计算CFRP索和钢索在脉动风荷载作用下的振动。需要说明的是，本文使用的脉动风未考虑风压的高度变化。

计算得到的索在脉动风场作用下的变形时程曲线如图11所示，由于脉动风场本身就很复杂，因此从变形时程曲线上难以直接判断钢索和CFRP索的优劣。因此，对图11中的6组12条曲线的进行统计，并用正态分布曲线去拟合，得到各条时程曲线的均值和方差如表3所示。从表3中可以看出，当初始应力=200MPa时，无论是钢索还是CFRP索振动的离散性都比较大，二者对比没有明显优劣之分。而当初始应力达到500MPa时，CFRP索振动的方差均明显小于钢索。分析其原因包括：①CFRP索质量轻频率高，吸收脉动风中低频能量较少；②CFRP索气弹阻尼高于钢索，进而振动中能量耗散更多。因此，虽然从概念上，CFRP索因为质量更轻，风致振动问题可能会更严重，但是在实际工程中，如果设计得当的话，CFRP索风振性能完全可能比钢索更好。

(a) 初始应力=200MPa，脉动风时程01 (b) 初始应力=200MPa，脉动风时程02

(e) 初始应力=500MPa，脉动风时程02 (f) 初始应力=500MPa，脉动风时程03

图11 脉动风场下索最大相对变形时程曲线

Fig.11 Time-history curves of maximal relative deformation of cables in fluctuant wind field

表3 脉动风场相对变形时程统计结果

Table 3 Statistic results of relative deformation of cables in fluctuant wind field

初始应力	脉动风时程	CFRP索			钢索
初始应力	脉动风时程	均值	方差	方差/均值	均值	方差	方差/均值
200MPa	脉动风时程01	0.395	0.228	0.577	0.399	0.295	0.739
	脉动风时程02	0.403	0.245	0.608	0.397	0.284	0.715
	脉动风时程03	0.386	0.295	0.764	0.392	0.234	0.597
500MPa	脉动风时程01	0.156	0.066	0.423	0.159	0.084	0.528
	脉动风时程02	0.158	0.063	0.399	0.158	0.089	0.563
	脉动风时程03	0.154	0.077	0.500	0.158	0.109	0.690

4 结论

本文利用通用有限元软件ANSYS提供的流固耦合计算功能，对CFRP索风振问题进行了数值分析，得到以下结论：

(1) ANSYS提供的湍流模型中，比较适合分析索风振问题的湍流模型是RNG模型和SZL模型；

(2) 在均匀风场作用下，CFRP索的气弹阻尼效果明显，气弹质量和气弹刚度效果较小；

(3) CFRP索的气弹阻尼比要高于同尺寸的钢索，且索的振幅越大、频率越高，气弹阻尼效果越明显；

(4) 在脉动风场作用下，CFRP索由于自振频率比同尺寸的钢索要高，且气弹阻尼比要大，如果设计合理，其风振效果可能会优于同尺寸的钢索。该结论对CFRP索在大跨结构中的应用有一定意义。

参考文献

1. 张元凯, 肖汝诚, FRP 材料在大跨度桥梁结构中的应用展望, 公路交通科技，2004, 21(4), 59-62.

（Zhang YK., Xiao RC., Application of FRP material in long span bridge, Journal of Highway and Transportation Research and Development, 2004, 21(4), 59-62.）

2. 汪胜义, 碳纤维复合材料(CFRP) 在桥梁工程中的应用及前景, 重庆交通学院学报，2005, 24(1), 30-32

（Wang SY., The application and future of carbon fiber reinforced polymer in bridge structure, journal of Chongqing Jiaotong University, 2005, 24(1), 30-32.）

3. 梅葵花，吕志涛，CFRP斜拉索的静力特性分析，中国公路学报，2004，17(2)，43-45.

（Mei KH., Lu ZT., Static characteristic analysis of CFRP cables, China Journal of Highway and Transport, 2004, 17(2), 43-45.）

4. 武岳, 考虑流固耦合作用的索膜结构风致振动相应研究，哈尔滨工业大学博士学位论文，2003.

5. 黄本才，结构抗风分析原理及应用，上海：同济大学出版社，2001.

6. 王福军，计算流体动力学分析——CFD软件原理与应用，北京：清华大学出版社，2004.

7. Tsuchiya M., Murakami S., Mochida A., Kondo K., Ishida Y., Development of a new k-e model for flow and pressure fields around bluff body, Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67&68: 169-182.

8. Murakami S., Overview of turbulence models applied in CWE-1997, Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 1-24.

9. Jeong UY., Koh HM., Lee HS., Finite element formulation for the analysis of turbulent wind flow passing bluff structures using the RNG k-e model. Journal of Wind Engineering and Industrial Aerodynamics. 2002, 90: 151–169.

10. Murakami S., Mochida A., On turbulent vortex shedding flow past 2D square cylinder predicted by CFD, Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54&55: 191-211.

11. Gluck M., Breuer M., Durst F., Halfmann A., Rank E., Computation of fluid-structure interaction on lightweight structures, Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89: 1351-1368.