|
大型连续刚构桥梁模型试验及损伤评估 黄盛楠，刘英奎，陆新征，叶列平 清华大学土木工程系，结构工程与振动教育部重点实验室，100084 第十七届全国桥梁学术会议论文集，2006.5，重庆: 907-913. 摘 要 桥梁结构在其服役过程中，由于荷载作用和各种环境不利因素的影响，结构不可避免的会产生累积损伤和功能退化，如不及时采取措施，甚至会导致突发事故。因此，对桥梁的工作状态进行实时监控，避免事故发生成为当前研究的一项热点。近年来，随着新型传感技术及通讯技术的发展，桥梁无损检测和健康监测成为研究热点。各种损伤评估理论在桥梁中开始得到应用。本文结合一个18m长3跨大型连续刚构桥梁模型试验，采用动力指纹法，对不同荷载工况下桥梁的损伤情况进行了识别。结果显示可以通过桥梁动力指纹的改变，初步判断其损伤情况，从而监测桥梁的工作状态。 关键词 桥梁 健康监测 动力指纹 损伤识别 |
|
1 引言 桥梁在其服役过程中，由于荷载作用和疲劳、腐蚀以及材料老化等各种不利因素的影响，结构将不可避免的产生累积损伤、抗力衰减、功能退化，如不及时采取措施，甚至导致突发事故[1]。近年来，公路桥梁超限行车现象特别严重，更加剧了桥梁结构疲劳累积损伤的发展。此外，使用期间可能出现各种不可预见灾害和意外事件（如车辆撞击等），也会导致桥梁结构的损伤或损坏。 根据已有文献，英国混凝土高速公路桥中的30%处于严重不良运行现状；根据美国高速公路联合委员会的统计数据，美国578000桥梁中将近40%存在结构缺陷或者功能陈旧，无法适应当今的交通发展[2]；据我国交通部公路司管理处提供的统计资料显示，截至2000年年底，全国公路及城市桥梁共有278，809座，其中危桥就有9，597座[3]。因此，桥梁安全运营现状已广泛引起世界各国的普遍重视。 避免桥梁事故发生的有效手段是对其进行健康监测，实时反应桥梁的运营状况，从而及时发出预警。近年来，随着新型传感技术及通讯技术的发展，桥梁无损检测和健康监测成为研究热点。动力指纹法、模型修正与系统识别法、神经网络法等损伤评估理论为健康监测提供依据。本文主要针对以受弯为主的混凝土桥梁结构，结合清华大学结构工程研究所进行的18m长3跨连续刚构桥模型试验，采用操作比较简单易行的动力指纹法对其进行损伤识别。结果表明对于此类结构，曲率模态是较为理想的损伤识别指标。 2 损伤识别理论 经过多年研究实践，各国学者提出过很多损伤识别方法，大致可以将其分为三类：动力指纹法、模型修正法和神经网络法[4,5,6]。其中模型修正法依赖于有限元模型，需要反演运算反复修正刚度矩阵，且需要求解逆问题，过程繁琐；神经网络法是20世纪80年代以来发展起来的，通过人工神经元网络的学习、训练、测试求解等步骤进行损伤识别，其前期运算量相当大，且不同的桥梁需要分别训练，普适性差；动力指纹法是将结构看作是由质量、刚度、阻尼等结构参数所组成的体系，通过结构模态参数和频响函数的变化来确定反映结构动力特性的相关参数的变化，从而判断结构是否发生损伤，其中常用的动力指纹有频响函数、频率、振型、曲率模态、应变模态、坐标确信准则(MAC)和坐标模态确信准则（COMAC）。本研究考虑到广泛普适性以及后期处理运算简单，选用动力指纹法进行损伤识别。 本文主要针对以受弯为主的桥梁结构，对于这类结构，曲率模态成为其动力响应的典型特征，且曲率模态对于损伤敏感，对于损伤定位更为准确[7,8]，因此本文对于模型桥在不同试验阶段的损伤分析也 是基于曲率模态。 曲率模态有两种测量方法：方法一是通过获得结构的应变反应直接换算成曲率关系，继而寻找其曲率模态；方法二是首先得到结构的位移模态，通过差分的方法获取其曲率模态[9]。本文采用加速度传感器进行结构动力性能的测量，然后根据方法二通过式（1）得到其曲率模态，再通过式（2）对损伤结构和完好结构的曲率模态差加以比较，从而对模型桥进行损伤定位。
式中， |
|
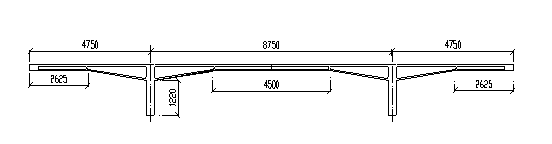
3 模型桥试验 3.1 模型桥简介 本试验的模型桥是轻质混凝土预应力连续刚构桥，其原型为云南安宁至楚雄高速公路14号达连坝段。原桥桥面总宽：0.1+0.5+净4.75+1.05+0.1=6.5m，设计荷载：汽-20，挂-100，人群荷载3.5kN/m2，混凝土标号为C50号，跨径为19m+35m+19m。模型桥按照1：4的相似比，并依据抗弯刚度相等的原则等效成T型截面，其各跨跨度为4.75＋8.75＋4.75＝18.25m（如图1所示），缩尺以后的模型桥通过施加配重使其与原桥在自重下产生的应力相等，图2为模型桥施加配重以后的照片。将模型桥的该状态作为桥梁完好状态，即损伤识别的原始比对状态。 图1 模型桥示意图 3.2 荷载工况及加载方案 在桥梁模型竣工以后进行了为期一个月的长期监测，该过程是将3t重的荷载堆放在桥梁中跨的跨中，观察桥梁的徐变等长期行为。 根据试验室的实际加载条件，共布置5个加载千斤顶。其中中间跨3个千斤顶，分别位于中跨跨中和距离南、北桥墩1.25m处，两个边跨各一个，均位于距离桥墩2.25m处。为接近桥梁实际工作情况，模拟车辆行驶荷载进行加载，从南向北依次组合相邻的千斤顶进行分级加载。整个加载过程共分为4种加载工况，如图3所示，其中加载工况A、B、C组合模拟车辆行驶过程。 试验加载按照工况ABC组合和工况D两个步骤进行。首先，依次按照工况A、B、C模拟车辆行驶荷载，加载分为桥梁在正常使用阶段开裂和车辆超载两个荷载分级。然后，按照工况D加载至破坏，破坏过程分为4个荷载步：桥梁开裂、超载、严重损坏、最终破坏，相应荷载参见表1。每级荷载步结束以后卸载再进行下一个荷载步。在实际加载过程中，考虑结构的对称性以及加载的操作简易性，将荷载步4与荷载步6对调。 图2 模型桥照片 图3 加载工况图 表1 试验加载方案设计
3.3 试验结果分析 3.3.1 加载前各阶段测试比较 在桥梁正式加载以前，对其在施工阶段的频率等动力特性进行了监测，包括张拉预应力前后、施加配重前后等，测量结果见表2。从结果可以看出张拉预应力对于桥梁的自振频率没有影响；配重增大了桥梁自身的重量，此时模型桥一阶、二阶频率分别降至11.12、23.5，将加配重以后的状态作为桥梁完好状态的参数，从而成为损伤分析的比对依据。 表2 加载前各阶段频率列表
从表2中可以看出，长期监测以后桥梁频率降低，其主要原因是开裂导致刚度降低。当长期荷载加至桥上以后，模型桥中跨的跨中附近已出现可见裂缝，荷载作用下结构在中跨跨中的长期变形达到1mm，长期荷载卸载以后部分裂缝闭合。为进一步进行损伤定位，将长期监测前后的振型、振型曲率进行比较。通过比较看出损伤前后振型几乎没有变化，即其对于损伤不敏感，不能作为损伤定位的参数；图4中给出损伤前后桥梁振型曲率差绝对值的曲线，明显看出在中跨跨中出现了较大峰值，预示损伤发生在模型桥的中跨跨中，与试验现象吻合。 图4 长期监测前后桥梁振型曲率的变化 注：图中横坐标桥梁跨度为标示点，其中点0、16分别代表北侧边支座和南侧边支座，4、12分别代表北桥墩和南桥墩，8代表中跨跨中，依此类推，后面图同。纵坐标仅为归一化以后的相对差值，不具备物理意义。 3.3.2 加载过程中各阶段测试比较 在桥梁的加载过程中，各荷载步后模型桥的自振频率如图5所示，可以看出每次加载对桥梁造成不同程度的损伤，导致频率有所降低，但降低程度不明显。为了更好地确定桥梁损伤随加载逐步发展的过程，并对损伤进行定位，下面将针对不同加载步对桥梁的振型曲率差进行比较。 图5 加载过程各阶段频率测试结果 荷载步1～荷载步3模拟桥梁在正常使用情况下裂缝逐步开展的阶段。荷载步1，当荷载达到30kN的时候，边跨的千斤顶下出现裂缝，开裂后模型桥刚度略有降低，当荷载加至37.5kN的时候，边跨千斤顶下方与桥墩之间裂缝开展均匀，该荷载步使得南侧边跨大范围开裂，对其损伤较大；荷载步2是一种最为不利的加载工况，当荷载达到20kN的时候在北侧桥墩上方的支座截面出现裂缝；荷载步3是刚度十分缓慢降低的过程，总体刚度降低很少，卸载以后残余变形几乎没有增加。 荷载步1与荷载步2的振型曲率差曲线如图6所示，由于荷载步3相对于荷载步2对桥梁损伤影响较小，因此不再对其振型曲率差进行测量比较。从图6中可以看出，荷载步1结束以后，桥梁中跨跨中以及南侧边跨损伤较为严重，其中中跨跨中的损伤主要是由于长期监测过程中的开裂造成的，南侧边跨的损伤主要是由于荷载步1过程中边跨的开裂引起的刚度降低；荷载步2的振型曲率差曲线中跨跨中的损伤略有增加，北侧桥墩处的损伤增加显著，这是由于荷载步2使得北侧桥墩处的支座截面开裂造成的，曲率模态法损伤识别的结果与试验现象相符。 图6 荷载步1～2桥梁振型曲率差的变化比较 荷载步4～荷载步6模型桥进入超载运营阶段。如前所述，考虑结构的对称性以及加载的操作简易性，将荷载步4与荷载步6对调，荷载步4仍在北侧三个千斤顶处加载。在整个超载运营过程中，随着荷载的增加，结构的刚度在不断降低，但卸载以后由于预应力筋的作用，残余变形增加缓慢。其中，在荷载步5的加载过程中，当荷载加至42kN的时候，跨中受拉钢筋屈服，结构进入屈服状态，刚度明显降低，当荷载达到45kN的时候，南侧桥墩柱顶钢筋屈服。 为分析模型桥承受超载荷载时的损伤情况，将荷载步4～荷载步6的振型曲率差进行比较，如图7所示。通过比较可以看出荷载步4使得北侧边跨产生一定损伤；荷载步5使得桥梁中跨跨中损伤明显加重，振型曲率差的峰值已由桥梁开裂状态（荷载步2）时的0.07发展到0.1，这是由于在前4个荷载步损伤主要是由于桥梁的开裂所引起的，而该荷载步的过程中，跨中受拉钢筋已经屈服，损伤的成因主要表现为钢筋屈服；而荷载步6在加重南侧边跨损伤的同时，也较大程度的增加了全桥的损伤，这是由于此时普通钢筋已经屈服，任何加载都会引起全桥的内力重分布，进而大幅度增加其他位置的损伤，该荷 图7 荷载步4～6桥梁振型曲率差的变化比较 图8 加载工况B下的振型曲率差绝对值 载步结束以后桥梁的损伤几乎对称（与累计加载历史吻合），中跨损伤最严重。可见，利用振型曲率差的方法可以识别出由于开裂、钢筋屈服等造成的损伤，且通过振型曲率差的峰值大小可以近似判断损伤的大小。 荷载步7～荷载步10则是根据加载工况D（如图3）进行的破坏性加载。其中，荷载步7是模拟正常使用阶段的荷载，单顶荷载仅加到37.5kN，远不及前面荷载步造成的损伤，因此没有进行振型曲率差的测量比较；荷载步8是模拟桥梁超载造成的中度损伤；荷载步9是模拟桥梁已经发生严重损伤的情况；荷载步10则是桥梁在无法使用情况下进行的一次动测。 由于前面多次加卸载已经对桥梁造成一定程度的损伤，荷载步7开始桥梁已经处于较为严重的损伤状态，且中跨跨中损伤最为严重，两侧边跨的损伤情况几乎对称分布。比较荷载步8～10的振型曲率差，其峰值略有增加，但增加不明显，原因在于：①，前面多次加卸载使得全桥开裂显著，由于裂缝造成的损伤已经基本上全部形成；②，荷载步5的时候普通钢筋已经屈服，由于屈服造成的损伤已经发生，且荷载步6已经将由于屈服造成的损伤发展到较大程度，加载工况D以前，桥梁已经处于较为严重的损伤阶段；③，反复加卸载对预应力筋的损伤很小，其仍处于弹性阶段，桥梁虽然已严重受损，但其卸载残余变形仍比较小，而且其再加载的刚度降低不是很多。 下面将最不利加载工况（加载工况B）下不同荷载步的振型曲率差情况进行比较，如图8所示。其中荷载步2对应的损伤情况为桥梁全面开裂，荷载步5对应的损伤情况为中跨跨中普通钢筋屈服，从图中可以清楚看出，荷载步5的振型曲率差峰值明显高于荷载步2，且峰值位置位于模型桥中跨跨中，可见曲率模态对于损伤定位以及损伤程度的定性分析具有很好的效果。 综上所述，曲率模态法可有效的对受弯为主的桥梁结构进行损伤识别，其损伤定位较为准确，且通过其峰值大小可大致判断损伤程度。 4 结论 本文针对清华大学18m长轻骨料混凝土连续梁刚构桥模型试验，分别对其长期徐变性能、正常使用阶段、超载阶段及破坏阶段进行损伤动测分析，利用曲率模态法对其进行损伤识别。通过分析，曲率模态法对于梁式桥的损伤较为敏感，具有较好的损伤定位功能，该方法对于由于混凝土开裂、普通钢筋屈服等原因引起的损伤具有识别能力。 通过本桥梁模型试验验证曲率模态法可应用于普通桥梁的健康监测，特别对于超载所造成的桥梁损伤具有较好的识别效果。 参考文献 [1] 欧进萍. 重大工程结构的累积损伤与安全评定.走上21 世纪的中国力学中国科协第9 次青年科学家论坛.北京清华大学出版社1996 179-189 [2] Li Y.D.(1997). Study on the assessment of existing bridge. Bridge Construction. (3) 18-21 [3] 张汎，崔玉萍. 旧桥的预测评估与维修加固. 2004北京国际桥梁结构评估研讨会，1-5 [4] 裴强，郭讯，张敏政. 桥梁健康监测及诊断研究综述. 地震工程与工程振动，2003，23(2): 61-67 [5] 李宏男，李东升.土木工程结构安全性评估、健康监测及诊断综述. 地震工程于工程振动， 2002，22（3）：82-90 [6] 李德葆,陆秋海.实验模态分析及其应用. 科学出版社，2001 [7] 李德葆，陆秋海，秦权. 承弯结构的曲率模态分析. 清华大学学报(自然科学版)，42(2)： 224-227 [8] Pandey A K, Biswas M, Samman M M. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, 1991, 145(2): 321-332 [9] 刘效尧，蔡键，刘晖. 桥梁损伤诊断. 人民交通出版社，2002 |
下载全文/PDF
Version
为
点的曲率模态值，
为
点的位移模态值，
为两点之间距离，
为基准距离，
为损伤识别指标
