|
And
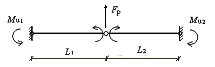
if there is more than one direct in which there are beams continuously pass
through the joint, the tie force in each direction can be obtained according
to the bending stiffness of beams in each direction:
 (6)
(6)
where:
j is the direction number, Ij is the rotational inertia
of beams in jth direction,
 is the tie force of beams in jth
direction.
is the tie force of beams in jth
direction.
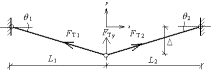
Finally,
in jth direction, the tie forc of beam can be obtained
from the balance of horizontal tie force at the joint:
 (7)
(7)
 (8)
(8)
where:
 and Lj1 are the tie force and the length of the first beam in
jth direction,
and Lj1 are the tie force and the length of the first beam in
jth direction,  and Lj2 are the tie force and the length of the second beam in jth
direction.
and Lj2 are the tie force and the length of the second beam in jth
direction.
4.3
Application and Verification
The
former 8-storey frame is redesigned by TF method proposed by this paper. There
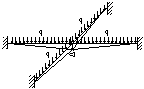
are three kinds of substructures in the structure, as seen in Figure. 7. For
the interior substructures, four beams provide tie forces in both two directions
because of their continuities (Figure. 7a). On the contrast, only two beams
provide tie forces for the side substructures (Figure. 7b). And both interior
and side substructures can provide beam mechanism and catenary mechanism to
prevent collapse. However, for corner substructure (Figure. 7c), only beam
mechanism can provide the collapse resistance capacity.
The
8-storeys frame after TF design satisfies the requirement of progressive collapse
resistance, and consumption of longitudinal steel bars is also listed in Table
2. It can be concluded that TF method in this paper is effective.
5
conclusions
AP
method and TF method are feasible for engineering design. NDAP method is the
most accurate methods but with high difficulty and complexity, so it is suitable
for very important and complicated structures. On the contrary, LSAP method
and TF method are easier to implement and their accuracy are guaranteed by
carefully choosing the factors and computational models. Based on a series
of rigorous researches, this paper suggests empirical factors, computational
models and design procedures of LSAP method and TF method on progressive collapse
resistance design for Chinese engineers.
ReferenceS
DoD. (2005). UFC 4-023-03: Design of Structures to
Resist Progressive Collapse.
Ellingwood, B. R. (2006).
Mitigating
Risk from Abnormal Loads and Progressive Collapse.
Journal of Performance
of Constructed Facilities,
20:4,315-323.
EuroCode 1. (2005). Actions on structures.Part 1.7:
General Actions - Accidental actions, European Committee for Standardization.
GB50010-2002. (2002). Code for Design of Concrete Structures,
Beijing: China Building Industry Press, China.
Liang, Y.,
Lu, X.Z., Miao, Z.W., Ye, L.P. (2007a). Progressive Collapse of Structures:
Introduction and Comparison of Standards. Proc. 6th National Conference
on Safety Protection for Engineering Structures, Luoyang, China, 195-200.
(in Chinese)
Liang,
Y., Lu, X.Z., Li, Y., Ye, L.P., Jiang, J.J. (2007b). Design Method to Resist
Progressive Collapse for a Three-story RC Frame. Journal of PLA University
of Science and Technology, 8:6, 659-664. (in Chinese)
Lu, X.Z.,
Zhang, Y.S., Jiang, J.J. (2007a). Simulation for the Collapse of Reinforced
Concrete Frame under Blast Load with Fiber Model, Blasting, 24:2, 1-6.
(in Chinese)
Lu, X.Z.,
Li, Y., Miao, Z.W., Chen, X.P., Liang, Y. (2007b). High Performance Simulation
for Building Structures under Disaster. Proc. 1st Symp on High Performance
Computing (HPC) Technology in Engineering Design. Shanghai, China, 93-101.
(in Chinese)
Wang, X.L.,
Lu, X.Z., Ye, L.P. (2007). Numerical Simulation for the Hysteresis Behavior
of RC Columns under Cyclic Loads. Engineering Mechanics, 4:12, 76-81.
Yi, W.J., He, Q.F., Xiao, Y. (2007). Collapse
Performance of RC Frame Structure. Journal of Building Structures,
28:5, 104-109. (in Chinese)
|




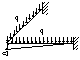

 (6)
(6)