1. 引言

近年来，随着核电的大力发展和大型商用飞机的广泛使用，飞机撞击核电站的风险大大增加。2009年6月12日，在美国“9.11”事件发生近8年后，一条由美国核管会颁布的联邦法规10CFR50.150“Aircraft Impact Assessment”使得抵御大型商用飞机撞击成为新建核电厂安全性评审的一项重要内容，该法规于当年7月13日正式开始生效^[1]。如今，飞机撞击核电站问题已经成为国际上研究的热点之一。

然而，飞机撞击核电站是个十分复杂的过程，其中涉及动力学碰撞、由于机翼燃油泄漏而引发的爆炸以及冲击振动对核电站内部设备的破坏作用等诸多问题。针对如此复杂的问题，已有研究尚未能提供较为成熟系统的研究手段和方法。1968年，Riera提出著名的冲击力方程^[2]，其本质为冲量定理的应用，该公式将飞机撞击问题简化为一维问题，对飞机正向碰撞刚性墙的理想状况，提供了一种简单实用的冲击力估算方式。为对该理论公式进行验证，1993年，日本的Kobori研究中心、日本电能工业中心研究院和美国的Sandia国家实验室进行了鬼怪F4战斗机原型机对靶体的撞击试验^[3]，撞击速度215 m/s，机身重量19 t，试验验证了Riera方法对于总撞击力计算的可靠性。

但理论公式适用范围十分局限，而撞击试验耗资巨大，实施困难。另一方面，计算机辅助工程和有限元基本理论在迅速发展，因此，近年来，数值模拟成为了研究此类大型复杂工程问题的主要手段。而研究飞机撞击核电站问题时，主要的模拟方法有两种。一种是非耦合方法：即直接将荷载时程曲线加载到安全壳的假定作用截面上，来进行结构动力响应分析；一种是耦合方法，也可称为“飞射物-靶体相互作用分析方法”，即同时建立安全壳和飞机模型，对其撞击的全过程进行数值模拟。

无论采用哪种方法，飞机撞击力的获取都是一个重要研究内容。已有的文献中虽然提供了通过理论推导或数值模拟所得到的一些常见飞机型号的撞击力时程曲线^[2-6]，但这些曲线仅针对某型飞机在某一特定速度下而言，而实际飞机的结构、荷载及速度千差万别。因此，掌握飞机撞击力时程曲线的获取方法及其规律是至关重要的。

2. 飞机有限元模型

本文所使用的飞机模型为波音公司的Boeing767-200ER^[7]，其载客量最多可达255~290（1级客舱布局），是典型的大型商用客机。“9.11”事件中，撞击世贸中心大楼的其中一架飞机型号即为Boeing767-200ER。

2.1 飞机几何外形

采用三维建模软件CATIA建立的飞机几何模型如图1所示。

2.2 对真实飞机的简化

真实的飞机内部结构十分复杂，几乎每个结构件都不尽相同，在数值模拟中，不可能精确到与真实飞机完全一致，必须做出合理的简化。根据Riera方程^[2]，可知飞机撞击力主要与飞机自身的质量分布及刚度分布有关：（1）刚度分布：影响飞机刚度的主要构件包括外蒙皮以及支撑这层蒙皮的“骨架”。对于机身而言，这些“骨架”包含机身框（环向支撑）、机身桁条（纵向支撑）、地板及地板梁（横向支撑），还有一些必要的隔断舱板；对于机翼及尾翼，这些“骨架”指机翼梁和翼肋；飞机发动机则利用两个近似圆柱形的壳体模拟；（2）质量分布：飞机质量分布情况如表1所示，由此可以得到飞机沿机身轴向的质量分布如图2所示。

表1 飞机有限元模型参数

2.3 复杂网格划分存在的问题及解决方法

几何模型建立好后，还需要对其进行网格划分、指定单元、赋予截面属性、材料属性等一系列操作，才能使其成为计算所需要的有限元模型，本文使用Hypermesh进行这部分工作。利用Hyermesh中的“line mesh”及“automesh”功能可以方便的进行一维和二维网格的划分。但网格划分过程中有两点需要注意：

（1）防止尺寸过小的单元出现。尽管已指定全局网格尺寸为250mm，但由于几何模型十分复杂，在某些部位仍有可能出现畸变严重、面积几乎为0的单元。显式运算的最小稳定时间步长 ，其中材料波速 ，而特征长度 是指最小的单元尺寸。可见计算时间很可能因为一个极小单元的存在而呈现数倍的增长。如图3所示，在图中的三角形单元附近有一个畸变十分严重的狭长单元，肉眼难以识别，这样的单元将导致非常漫长的计算时间。可以采用的解决办法是使用Hypermesh中的check element功能，筛选这些不合规定的单元，对其进行重新划分，获得较为均匀的网格，从而大大缩短计算时长。

图3 模型中的过小单元

（2）确保连接处的节点耦合。真实飞机的结构件，如框、梁等，是通过铆接的形式固定到蒙皮上的，在有限元模拟中，可通过共节点来模拟固接。需要指出的是，有时候节点仅仅是看上去似乎已经耦合了，但实际上仍然是位于同一位置的两个节点，这时可利用Hypermesh中的Equivalence功能，指定一个合适的容差范围，如果两个节点之间的距离在容差范围内而又没有重合，则会用黄色点标记出来，如图4所示。这样的连接形式是无效的，在计算时，可以发现一旦机翼发生了变形，发动机马上就会与机翼分离。因此，网格划分完毕后，一定要利用Equivalence功能对连接处节点进行耦合。

图4 未耦合节点导致连接失效

2.4 LS-DYNA中复杂截面梁的定义

Hypermesh中定义LS-DYNA中的复杂梁单元需要利用*SECTION_BEAM和*INTEGRATION_BEAM两个关键字卡片，其中，*SECTION_BEAM用以定义截面基本属性，对于矩形或环形这两种简单截面，直接在*SECTION_BEAM中定义即可。但对于I型、C型及其它复杂形状的截面，则需要首先利用*INTEGRATION_BEAM来定义其积分规则，再在*SECTION_BEAM中的QR/IRID中选择定义的积分规则，并将CST的值设为2^[8]。

最终建立的飞机有限元模型如图5所示，飞机全局网格尺寸约为250 mm，壳单元和梁单元采用共节点建模：其中壳单元总数约5万，单元类型为SHELL163；梁单元总数约为2.2万，单元类型为BEAM161，梁截面尺寸如表2所示。

2.5 飞机材料模型及参数

无论是飞机机身的铝合金材料还是发动机的钢材，在碰撞的情况下材料的率效应都是不可忽略的。Johnson_Cook（LS-DYNA中的MAT015）是一个能反映应变硬化、应变率强化效应和温度软化效应的理想刚塑性强度模型，适用于描述金属材料在大变形、高应变率和高温条件下的本构模型^[9]。钢材及铝合金的基本材料属性如表3所示，表4为MAT015的各项材料参数^[10]。

(a)飞机外层蒙皮壳单元                   (b)飞机内部结构壳单元及梁单元

图5 飞机有限元模型

表2 内部梁结构参数

然而，LS-DYNA中Johnson_Cook模型不能用于梁单元，因此，本研究对壳单元使用Johnson_Cook模型，而对梁单元采用Plastic_Kinematic模型。Plastic_Kinematic模型对应LS-DYNA中的MAT03模型，也是常用的考虑了塑性流动、率效应和失效的金属本构模型，本文中内部梁结构均采用铝合金材料，其MAT03参数如表5所示^[11]。

表3 钢材及铝合金的材料属性

表4 MAT015参数

表5 MAT03参数

3. 飞机撞击刚性墙数值模拟

本文着重探讨飞机自身结构及撞击速度对撞击力的影响，因此考虑靶体为刚性墙的较简单情况，同时也是为了验证飞机有限元模型及碰撞模拟方法的合理性，为今后深入研究飞机撞击核电站问题奠定基础。

所建立的有限元模型如图6所示。

其中刚性墙的网格密度为1000 mm，采用刚性材料模型*MAT_RIGID，通过设定CON1和CON2的值分别限定刚性墙三个方向的平动自由度和转动自由度。设定三个自动接触类型：包括飞机梁结构与刚性墙的接触*CONTACT_AUTOMATIC_BEAMS_TO_SURFACE；飞机壳结构与刚性墙的接触*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE（飞机壳单元为从面，刚性墙为主面）；以及飞机由于发生大变形导致的自接触*CONTACT_AUTOMATIC_SINGLE_SURFACE，程序自动搜索发生自接触的节点。

设置关键字*CONTROL_ENERGY，要求计算沙漏能，并计入能量平衡中，利用关键字*CONTROL_HOURGLASS进行沙漏控制。在*CONTROL_TERMINATION中，可以设定计算终止时间，根据本文中不同的飞机初始速度，该值可设定在0.3 s~0.5 s范围之内。

在输出*DATABASE选项中，可选择感兴趣的结果输出，如撞击力可以通过*DATABASE_ASCII_RCFORC输出，为了检验能量平衡关系等，可以利用*DATABASE_ASCII_GLSTATS输出全局数据。这里我们选择输出数据的时间间隔为0.001 s，那么对于一个0.3 s的碰撞过程来说，将输出300步的结果。

初始速度可通过关键字INITIAL_VELOCITY_GENERATION来设定，这里飞机速度沿自身轴线方向水平向前飞行，即Y轴负方向。

选取200 m/s作为飞机的初始撞击速度。撞击过程的能量变化图如图7所示。从图7可看出，整个撞击过程总能量基本保持不变，满足能量守恒。而沙漏能仅占总能量的不到5%，说明沙漏得到了有效的控制。撞击过程中，动能不断转换为内能，一部分动能和内能随着飞机碎片的飞出而损失了。动能和内能的曲线在约0.08 s和0.16 s时刻有两个明显的拐点，对照图8的撞击荷载时程曲线可发现在约0.08 s时刻，发动机接触上刚性墙，由于发动机刚度和质量都很大，此时撞击力突增，故导致了动能的迅速下降，在0.08 s至0.16 s的时间段内，是发动机及机翼与刚性墙接触的过程，这时的撞击力达到峰值，到0.16 s时刻，机翼已完全与刚性墙接触，此时的撞击力迅速下降，导致了图7中动能减少的速度变慢。到了0.25 s时，整个飞机已近乎被压碎，这时飞机已基本没有速度，撞击力几乎为0。

图8 飞机撞击力时程曲线及各时刻的变形情况（V=200 m/s）

4. 飞机撞击力影响因素

4.1 撞击速度

本文对飞机以100 m/s、150 m/s、200 m/s、250 m/s及300 m/s这五种不同的速度撞击所得的荷载时程曲线进行了比较，如图9所示。初始速度越大，则撞击力峰值越高，峰值出现时间越早，当初始速度为最大值300 m/s时，撞击力峰值达到410 MN。

为进一步说明撞击力峰值与初始速度之间的关系，令速度平方比 ，撞击力峰值比 。其中 是初始速度， 是最大初始速度，即300 m/s； 是撞击力峰值， 指初始速度300 m/s时所对应的撞击力峰值410 MN。由表6可见撞击力峰值比与初始速度平方比十分接近，说明撞击力峰值与初始速度的平方近似呈线性关系。

4.2 飞机结构刚度

为分析飞机内部结构对其撞击力的影响，本文在图5所示的模型基础上进行简化得到了另外两个飞机模型，三个模型重量分布情况一致，仅内部结构精细程度有所不同。其中模型3包括所有的梁单元和壳单元，为最精确的模型，即图5中所示；模型2相对模型3，只建立了所有壳单元的模型，而没有相应的梁单元模型；模型1对模型2进一步简化，只有外层蒙皮的壳单元，而没有内部翼肋、地板、隔断舱板等结构的壳单元（图10）。

(a) 模型1                       (b) 模型2                             (c) 模型3

图10 不同精细程度的飞机模型

图11 模型1、2、3的撞击力及冲量时程曲线（V=100 m/s）

图12 模型1、2、3的撞击力及冲量时程曲线（V=150 m/s）

针对100 m/s及150 m/s这两种初始速度下的三个模型的撞击力及冲量进行了比较,结果分别如图11及图12所示。不同模型之间的撞击力时程曲线形状虽有一定差别，但峰值基本相当，而利用撞击力对时间进行积分得到对应冲量，可发现在初始速度为100 m/s时，模型1的冲量最小，模型3的冲量最大，相差约5%（图11），而当撞击速度增大至150 m/s时，这种差别变得很不明显，三个模型的冲量几乎一致（图12）。

此组对比说明在较低的速度下，飞机结构对撞击力的影响较高速情况更为明显，而飞机袭击核电站时，离地高度很低，低速飞行的情况更有可能发生。因此，飞机内部结构对于撞击破坏的影响有必要给予考虑。

5. 结论

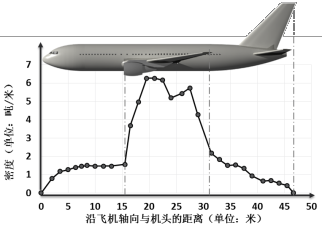
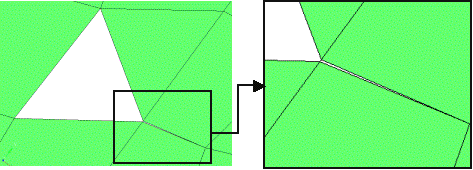
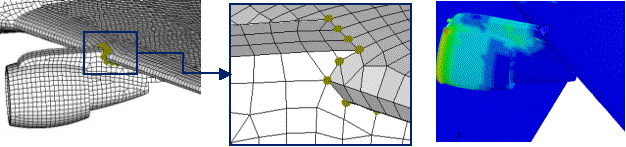
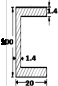
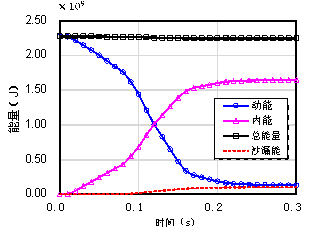
本文从真实飞机模型的简化、几何模型建立、网格划分及材料模型的选取等各方面详细介绍了飞机有限元模型的建立过程，通过飞机撞击刚性墙的数值模拟，对飞机有限元模型及碰撞模拟方法均进行了验证，掌握了飞机撞击力的一些基本规律，针对撞击刚性墙的情况，得到了一些实用的结论:

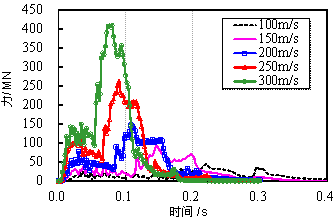
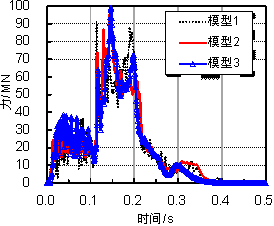
（1）飞机撞击力峰值与速度平方近似呈线性关系；

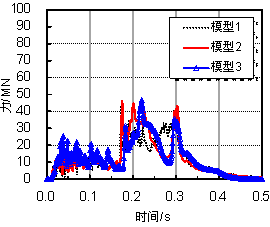
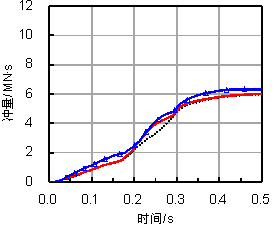
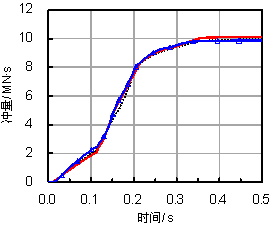
（2）飞机自身结构刚度对撞击冲量有影响，刚度越大，则冲量越大，并且在较低速度下，这种差异更为明显。因此，在核电站设计时，出于安全考虑，飞机内部结构对于撞击破坏的影响有必要给予考虑。

采用数值方法研究飞机撞击核电站问题时，飞机有限元模型十分关键，建立一个考虑内部结构的精细飞机有限元模型是十分必要的，文中关于飞机有限元模型建立的详细介绍及撞击力的分析结果为今后此类问题的进一步研究提供了参考。

致 谢

感谢基金项目：大型先进压水堆核电站国家科技重大专项CAP1400安全评审技术及独立验证试验（编号：2011ZX06002-10）及国家自然科学基金（编号：51222804)对本文工作的支持。

参考文献

[1]       汤搏. 关于核电厂防大型商用飞机撞击的要求[J]. 核安全, 2010, 3(003): 1-16. 

[2]       Riera J D. On the stress analysis of structures subjected to aircraft impact forces [J]. Nuclear Engineering and Design, 1968, 8(4): 415-426.

[3]       Sugano T, Tsubota H, Kasai Y, et al. Full-scale aircraft impact test for evaluation of impact force [J]. Nuclear Engineering and Design, 1993, 140(3): 373-385.

[4]       Iliev V, Georgiev K, Serbezov V. Assessment of impact load curve of Boeing 747-400 [J]. MTM Virtual J.1,2011, 22-25.

[5]       Siefert A, Henkel F O. Nonlinear analysis of commercial aircraft impact on a reactor building[J]. Transactions, SMiRT, 2011, 21: 6-11.

[6]       Jin B M, Lee Y S, et al. Development of finite element model of large civil aircraft engine and application to the localized damage evaluation of concrete wall crashed by large civil aircraft [J]. Transactions of the 21^st SMiRT, 2011.

[7]       http://www.boeing.com

[8]       Livermore Software Technology Corporation(LSTC).LS-DYNA971 keyword user’s manual, volume I.2007.

[9]       Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.

[10]    Wierzbicki T, Teng X. How the airplane wing cut through the exterior columns of the World Trade Center[J]. International Journal of Impact Engineering, 2003, 28(6): 601-625.

[11]    刘晶波, 郑文凯. 大型商用飞机撞击核电站屏蔽厂房荷载研究[J]. 振动与冲击, 2014, 33(06)：98-101

作者信息：林丽(1989－)，女，广西人，硕士研究生，主要从事结构非线性计算和仿真研究。

E-mail: l-lin07@mails.tsinghua.edu.cn

通讯作者：陆新征(1978－)，男，安徽人，博士，教授，主要从事结构非线性计算和仿真研究。

E-mail:luxz@mail.tsinghua.edu.cn。