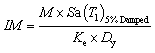|
6. Summary and Conclusions
This paper utilizes the IDA-based
collapse fragility evaluation approach to quantitatively assess the seismic
capacity of SDOF systems to resist sidesway collapse and proposes the concept
of collapse capacity spectrum, which is a rational extension of the classical
inelastic response spectrum. The calculation procedure and engineering significance
of the collapse capacity spectrum are illustrated. The collapse capacity spectrum
provides a quantitative estimation for the collapse capacity of SDOF systems.
This spectrum will be helpful to provide a direct analytical basis for collapse
safety margin and also to facilitate the static pushover-based approximate
methods of collapse evaluation. Through a systematic parametric discussion
on the collapse capacity spectrum, the major findings of this study are summarized
below:
(i) Fundamental periods are important
factors for the collapse capacity, and ductile structures generally have high
collapse capacity but are more sensitive to RTR uncertainty.
The influence of the post-capping stiffness on the collapse capacity spectrum
is generally insignificant compared to that of the ductility ratio. When the softening ratio ac is greater than 1.0, its influence
is negligible.
(ii) The ductility capacity and
P-D effect are important factors in collapse evaluation, whereas the pinching
effect is essentially negligible in
collapse evaluation. The cyclic deterioration effect depends on the structural
ductility capacity, i.e. it is negligible for non-ductile structures while it considerably degrades the collapse
capacity for ductile structures.
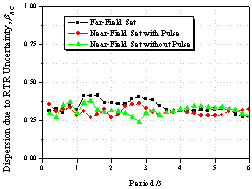
(iii) The influence of earthquake
ground motions on the collapse resistance capacity of SDOF systems depends
on the fundamental period. Structures with fundamental periods ranging from
0.4 s to 1.8 s are more vulnerable to the near-field pulse-like ground motions
and structures with fundamental periods ranging from 2.6 s to 5 s are more
vulnerable to the far-field ones.
Acknowledgements
The authors are grateful for the
financial support received from the National Key Technology R&D Program
(No. 2013BAJ08B02), and the National Nature Science Foundation of China (No.
51222804, 51178249, 51378299).
Reference
Adam, C. and Jäger, C. (2012). ¡°Seismic collapse capacity
of basic inelastic structures vulnerable to the P-delta effect¡±, Earthquake
Engineering & Structural Dynamics, Vol. 41, No. 4, pp. 775-793.
Araki, Y. and Hjelmstad, K.D. (2000). ¡°Criteria for assessing
dynamic collapse of elastoplastic structural systems¡±, Earthquake Engineering
& Structural Dynamics, Vol. 29, No. 8, pp. 1177-1198.
Asimakopoulos, A.V., Karabalis, D.L. and Beskos, D.E. (2007).
¡°Inclusion of P-¦¤ effect in displacement-based seismic design of steel moment
resisting frames¡±, Earthquake Engineering & Structural Dynamics,
Vol. 36, No. 14, pp. 2171-2188.
Bernal, D. (1987). ¡°Amplification factors for inelastic
dynamic p-¦¤ effects in earthquake analysis¡±, Earthquake Engineering &
Structural Dynamics, Vol. 15, No. 5, pp. 635-651.
Bernal, D. (1992). ¡°Instability
of Buildings Subjected to Earthquakes¡±, Journal of Structural Engineering,
Vol. 118, No. 8, pp. 2239-2260.
Brookshire, D.S., Chang, S.E., Cochrane, H., Olson, R.A.,
Rose, A. and Steenson, J. (1997). ¡°Direct and indirect economic losses from
earthquake damage¡±, Earthquake Spectra, Vol. 13, No. 4, pp. 683-701.
Chakraborti, A. and Gupta, V.K. (2005). ¡°Scaling of strength
reduction factors for degrading elasto-plastic oscillators¡±, Earthquake
Engineering & Structural Dynamics, Vol. 34, No. 2, pp. 189-206.
Champion, C. and Liel, A. (2012). ¡°The effect of near-fault
directivity on building seismic collapse risk¡±, Earthquake Engineering
& Structural Dynamics, Vol. 41, No. 10, pp. 1391-1409.
Chopra, A.K. (2001). Dynamic of Structures-Theory and
Applications to Earthquake Engineering, Prentice Hall, New Jersey, USA.
Chopra, A.K. and Chintanapakdee, C. (2001). ¡°Comparing response
of SDF systems to near-fault and far-fault earthquake motions in the context
of spectral regions¡±, Earthquake Engineering & Structural Dynamics,
Vol. 30, No. 12, pp. 1769-1789.
Clough, R.W. and Johnston, S.B. (1966). ¡°Effect of stiffness
degradation on earthquake ductility requirements¡±, Proceedings of Japan
Earthquake Engineering Symposium, Tokyo, Japan.
DesRoches, R., Comerio, M., Eberhard, M., Mooney, W. and
Rix, G.J. (2011). ¡°Overview of the 2010 Haiti Earthquake¡±, Earthquake Spectra,
Vol. 27, No. S1, pp. 1-21.
Fajfar, P. and Dolšek, M. (2011). ¡°A practice-oriented
estimation of the failure probability of building structures¡±, Earthquake
Engineering & Structural Dynamics, Vol. 41, No. 3, pp. 531-547.
FEMA (2004). FEMA P450: NEHRP Recommended Provisions
and Commentary for Seismic Regulations for New Buildings and Other Structures,
Federal Emergency Management Agency, Washington, USA.
FEMA (2009). FEMA P695: Quantification of building seismic
performance factors, Federal Emergency Management Agency, Washington,
USA.
Goulet, C.A., Haselton, C.B., Mitrani-Reiser, J., Beck,
J.L., Deierlein, G.G., Porter, K.A. and Stewart, J.P. (2007). ¡°Evaluation
of the seismic performance of a code-conforming reinforced-concrete frame
building-from seismic hazard to collapse safety and economic losses¡±, Earthquake
Engineering & Structural Dynamics, Vol. 36, No. 13, pp. 1973-1997.
Han, S.W., Moon, K.H. and Chopra, A.K. (2010). ¡°Application
of MPA to estimate probability of collapse of structures¡±, Earthquake Engineering
& Structural Dynamics, Vol. 39, No. 11, pp. 1259-1278.
Haselton, C.B., Liel, A.B., Deierlein, G.G., Dean, B.S.
and Chou, J.H. (2010). ¡°Seismic collapse safety of reinforced concrete buildings.
I: Assessment of ductile moment frames¡±, Journal of Structural Engineering,
Vol. 137, No. 4, pp. 481-491.
Ibarra, L.F., Medina, R.A. and Krawinkler, H. (2005). ¡°Hysteretic
models that incorporate strength and stiffness deterioration¡±, Earthquake
engineering & structural dynamics, Vol. 34, No. 12, pp. 1489-1511.
Ibarra, L.F. and Krawinkler, H. (2011). ¡°Variance of collapse capacity
of SDOF systems under earthquake excitations¡±, Earthquake engineering &
structural dynamics, Vol. 40, No. 12, pp. 1299-1314.
Jäger, C. and Adam, C. (2013). ¡°Influence of Collapse Definition
and Near-Field Effects on Collapse Capacity Spectra¡±, Journal of Earthquake
Engineering, Vol. 17, No. 6, pp. 859-878.
Kato, B.A. (Ye, L.P. and Pei, X.Z., Trans.) (2010). Earthquake-Resistant
Design Method for Buildings Based on Energy Balance, Tsinghua University
Press, Beijing, China.
Kircher, C.A., Reitherman, R.K., Whitman, R.V. and Arnold,
C. (1997). ¡°Estimation of earthquake losses to buildings¡±, Earthquake Spectra,
Vol. 13, No. 4, pp. 703-720.
Kiureghian, A.D. and Ditlevsen, O. (2009). ¡°Aleatory or
epistemic? Does it matter? ¡±, Structural Safety, Vol. 31, No. 2, pp.
105-112.
Krawinkler, H. and Zareian, F. (2007). ¡°Prediction of collapse-How
realistic and practical is it, and what can we learn from it? ¡±, The Structural
Design of Tall and Special Buildings, Vol. 16, No. 5, pp. 633-653.
Lee, L.H., Han, S.W. and Oh, Y.H. (1999). ¡°Determination
of ductility factor considering different hysteretic models¡±, Earthquake
Engineering & Structural Dynamics, Vol. 28, No. 9, pp. 957-977.
Liel, A.B., Haselton, C.B. and Deierlein, G.G. (2010). ¡°Seismic
collapse safety of reinforced concrete buildings. II: Comparative assessment
of nonductile and ductile moment frames¡±, Journal of Structural Engineering,
Vol. 137, No. 4, pp. 492-502.
Lu, X.Z., Ye, L.P., Ma, Y.H. and Tang, D.Y. (2012). ¡°Lessons
from the collapse of typical RC frames in Xuankou School during the great
Wenchuan Earthquake¡±, Advances in Structural Engineering, Vol. 15,
No. 1, pp. 139-154.
Luco, N., Ellingwood, B.R., Hamburger, R.O., Hooper, J.D.,
Kimball, J.K. and Kircher, C.A. (2007). ¡°Risk-targeted versus current seismic
design maps for the conterminous United States¡±, Proceedings of Structural
Engineers Association of California 2007 Convention, Lake Tahoe, CA.
Mahin, S.A. and Bertero, V.V. (1976). ¡°Nonlinear seismic
response of a coupled wall system¡±, Journal of the Structural Division,
Vol. 102, No. 9, pp. 1759-1780.
Malhotra, P.K. (1999). ¡°Response of buildings to near-field
pulse-like ground motions¡±, Earthquake Engineering & Structural Dynamics,
Vol. 28, No. 11, pp. 1309-1326.
Mehanny, S.S. (1999). Modeling and assessment of seismic
performance of composite frames with reinforced concrete columns and steel
beams, Ph.D. Thesis, Department of Civil and Environment Engineering,
Stanford University, Stanford, CA.
Miranda, E. and Akkar, S.D. (2003). ¡°Dynamic instability
of simple structural systems¡±, Journal of Structural Engineering, Vol.
129, No. 12, pp. 1722-1726.
Miranda, E. and Ruiz-Garc¨ªa, J. (2002). ¡°Evaluation of approximate
methods to estimate maximum inelastic displacement demands¡±, Earthquake
Engineering & Structural Dynamics, Vol. 31, No. 3, pp. 539-560.
Rahnama, M. and Krawinkler, H. (1993). Effects of soft
soil and hysteresis model on seismic demands, Blume Earthquake Engineering
Center Report No. 108, Department of CEE, Stanford University: Stanford.
Riddell, R. (2008). ¡°Inelastic response spectrum: early
history¡±, Earthquake Engineering & Structural Dynamics, Vol. 37,
No. 8, pp. 1175-1183.
Shafei, B., Zareian, F. and Lignos, D.G. (2011). ¡°A simplified
method for collapse capacity assessment of moment-resisting frame and shear
wall structural systems¡±, Engineering Structures, Vol. 33, No. 4, pp.
1107-1116.
Takizawa, H. and Jennings, P.C. (1980). ¡°Collapse of a model
for ductile reinforced concrete frames under extreme earthquake motions¡±,
Earthquake Engineering & Structural Dynamics, Vol. 8, No. 2, pp.
117-144.
Tang, B., Lu, X., Ye, L.P. and Shi, W. (2011). ¡°Evaluation
of collapse resistance of RC frame structures for Chinese schools in seismic
design categories B and C¡±, Earthquake Engineering and Engineering Vibration,
Vol. 10, No. 3, pp. 369-377.
Tong, G. and Zhao, Y. (2007). ¡°Seismic force modification
factors for modified-Clough hysteretic model¡±, Engineering Structures,
Vol. 29, No. 11, pp. 3053-3070.
Vamvatsikos, D. and Cornell, C.A. (2002). ¡°Incremental dynamic
analysis¡±, Earthquake Engineering & Structural Dynamics, Vol. 31,
No. 3, pp. 491-514.
Vamvatsikos, D. and Cornell, C.A. (2004). ¡°Applied incremental
dynamic analysis¡±, Earthquake Spectra, Vol. 20, No. 2, pp. 523-553.
Vamvatsikos, D. and Cornell, C.A. (2005). ¡°Direct Estimation
of seismic demand and capacity of multidegree-of-freedom systems through incremental
dynamic analysis of single degree of freedom approximation¡±, Journal of
Structural Engineering, Vol. 131, No. 4, pp. 589-599.
Vian, D. and Bruneau, M. (2003). ¡°Tests to structural collapse
of single degree of freedom frames subjected to earthquake excitations¡±, Journal
of Structural Engineering, Vol. 129, No. 12, pp. 1676-1685.
Williamson, E.B. (2003). ¡°Evaluation of damage and P-¦¤ effects
for systems under earthquake excitation¡±, Journal of Structural Engineering,
Vol. 129, No. 8, pp. 1036-1046.
Ye, L.P., Lu, X.Z. and Li, Y. (2010). ¡°Design objectives
and collapse prevention for building structures in mega-earthquake¡±, Earthquake
Engineering and Engineering Vibration, Vol. 9, No. 2, pp. 189-199.
Ye, L.P., Ma, Q.L., Miao, Z.W., Guan, H. and Zhuge, Y. (2013).
¡°Numerical and comparative study of earthquake intensity indices in seismic
analysis¡±, The Structural Design of Tall and Special Buildings, Vol.
22, No. 4, pp. 362-381.
Zareian, F. and Krawinkler, H. (2007). ¡°Assessment of probability
of collapse and design for collapse safety¡±, Earthquake Engineering &
Structural Dynamics, Vol. 36, No. 13, pp. 1901-1914.
Zareian, F. and Krawinkler, H. (2010). ¡°Structural system
parameter selection based on collapse potential of buildings in earthquakes¡±,
Journal of Structural Engineering, Vol. 136, No. 8, pp. 933-943.
Zareian, F., Krawinkler, H., Ibarra, L. and Lignos, D. (2010).
¡°Basic concepts and performance measures in prediction of collapse of buildings
under earthquake ground motions¡±, The Structural Design of Tall and Special
Buildings, Vol. 19, No. 1-2, pp. 167-181.
Zhao, B., Taucer, F. and Rossetto, T. (2009). ¡°Field investigation
on the performance of building structures during the 12 May 2008 Wenchuan
earthquake in China¡±, Engineering Structures, Vol. 31, No. 8, pp. 1707-1723.
List of Tables
Table 1.
Model Identifier and Modeling Parameters
List of figures
Figure 1.
Description of the hysteretic model
Figure 2.
Hysteretic curves for various g values
Figure 3.
Simulation of the P-D effect
Figure 4.
Collapse capacity
assessment of SDOF systems
Figure 5.
Dynamic pushover
curves for SDOF systems with various fundamental periods
Figure 6.
Collapse Capacity Spectrum
Figure 7.
Influence of the ductility ratio m on collapse capacity spectrum (as=0.00,
ac=1.0, kf=1.0,
g=Infinity, q=0.00)
Figure 8.
Influence of the softening ratio ac on collapse capacity spectrum (as=0.00, m=4.0, kf=1.0, g=Infinity,
q=0.00)
Figure 9.
Influence of the pinching property on collapse capacity spectrum
(as=0.00, m=4.0, ac=1.0,
g=Infinity, q=0.00)
Figure 10.
Effect of the cyclic deterioration property on collapse capacity
spectrum (as=0.00, ac=1.0,
kf=1.0, q=0.00)
Figure 11.
Effect of the P-D
Effect on collapse capacity spectrum (as=0.00, m =4.0, ac=1.0,
kf=1.0, g=Infinity)
Figure 12.
Collapse capacity spectrum with different
ground motion input
Table 1. Model Identifier and Modeling Parameters
|
Model ID
|
as
|
m
|
ac
|
kf
|
kd
|
g
|
q
|
|
Model 1 (benchmark)
|
0.0
|
4.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 2
|
0.0
|
2.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 3
|
0.0
|
3.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 4
|
0.0
|
5.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 5
|
0.0
|
6.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 6
|
0.0
|
4.0
|
0.5
|
No Pinching
|
Infinity
|
0.00
|
|
Model 7
|
0.0
|
4.0
|
1.5
|
No Pinching
|
Infinity
|
0.00
|
|
Model 8
|
0.0
|
4.0
|
2.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 9
|
0.0
|
4.0
|
2.5
|
No Pinching
|
Infinity
|
0.00
|
|
Model 10
|
0.0
|
4.0
|
3.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 11
|
0.0
|
4.0
|
1.0
|
0.8
|
1.0
|
Infinity
|
0.00
|
|
Model 12
|
0.0
|
4.0
|
1.0
|
0.6
|
1.0
|
Infinity
|
0.00
|
|
Model 13
|
0.0
|
4.0
|
1.0
|
0.4
|
1.0
|
Infinity
|
0.00
|
|
Model 14
|
0.0
|
4.0
|
1.0
|
0.2
|
1.0
|
Infinity
|
0.00
|
|
Model 15
|
0.0
|
4.0
|
1.0
|
0.8
|
0.5
|
Infinity
|
0.00
|
|
Model 16
|
0.0
|
4.0
|
1.0
|
0.6
|
0.5
|
Infinity
|
0.00
|
|
Model 17
|
0.0
|
4.0
|
1.0
|
0.4
|
0.5
|
Infinity
|
0.00
|
|
Model 18
|
0.0
|
4.0
|
1.0
|
0.2
|
0.5
|
Infinity
|
0.00
|
|
Model 19
|
0.0
|
4.0
|
1.0
|
0.8
|
0.0
|
Infinity
|
0.00
|
|
Model 20
|
0.0
|
4.0
|
1.0
|
0.6
|
0.0
|
Infinity
|
0.00
|
|
Model 21
|
0.0
|
4.0
|
1.0
|
0.4
|
0.0
|
Infinity
|
0.00
|
|
Model 22
|
0.0
|
4.0
|
1.0
|
0.2
|
0.0
|
Infinity
|
0.00
|
|
Model 23
|
0.0
|
4.0
|
1.0
|
No Pinching
|
500
|
0.00
|
|
Model 24
|
0.0
|
4.0
|
1.0
|
No Pinching
|
300
|
0.00
|
|
Model 25
|
0.0
|
4.0
|
1.0
|
No Pinching
|
100
|
0.00
|
|
Model 26
|
0.0
|
4.0
|
1.0
|
No Pinching
|
50
|
0.00
|
|
Model 27
|
0.0
|
4.0
|
1.0
|
No Pinching
|
25
|
0.00
|
|
Model 28
|
0.0
|
2.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 29
|
0.0
|
2.0
|
1.0
|
No Pinching
|
500
|
0.00
|
|
Model 30
|
0.0
|
2.0
|
1.0
|
No Pinching
|
300
|
0.00
|
|
Model 31
|
0.0
|
2.0
|
1.0
|
No Pinching
|
100
|
0.00
|
|
Model 32
|
0.0
|
2.0
|
1.0
|
No Pinching
|
50
|
0.00
|
|
Model 33
|
0.0
|
2.0
|
1.0
|
No Pinching
|
25
|
0.00
|
|
Model 34
|
0.0
|
6.0
|
1.0
|
No Pinching
|
Infinity
|
0.00
|
|
Model 35
|
0.0
|
6.0
|
1.0
|
No Pinching
|
500
|
0.00
|
|
Model 36
|
0.0
|
6.0
|
1.0
|
No Pinching
|
300
|
0.00
|
|
Model 37
|
0.0
|
6.0
|
1.0
|
No Pinching
|
100
|
0.00
|
|
Model 38
|
0.0
|
6.0
|
1.0
|
No Pinching
|
50
|
0.00
|
|
Model 39
|
0.0
|
6.0
|
1.0
|
No Pinching
|
25
|
0.00
|
|
Model 40
|
0.0
|
4.0
|
1.0
|
No Pinching
|
Infinity
|
0.04
|
|
Model 41
|
0.0
|
4.0
|
1.0
|
No Pinching
|
Infinity
|
0.08
|
|
Model 42
|
0.0
|
4.0
|
1.0
|
No Pinching
|
Infinity
|
0.12
|
|
Model 43
|
0.0
|
4.0
|
1.0
|
No Pinching
|
Infinity
|
0.16
|
|
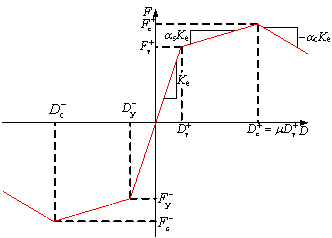
|
|
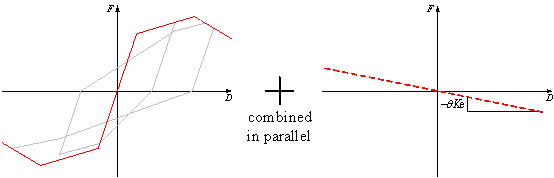
(a) Trilinear
backbone curve
|
|
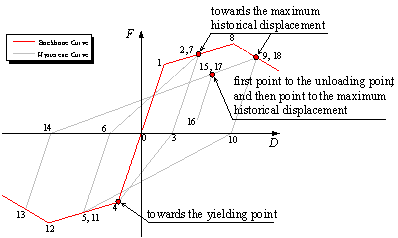
|
|
(b) Basic hysteretic rule
|
|
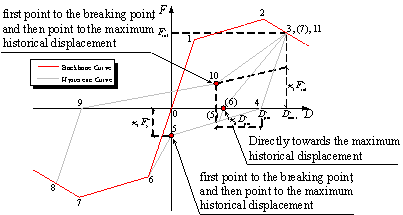
|
|
(c) Simulation
of the pinching property
|
|
Figure 1 Description
of the hysteretic model
|
|
|
|
|
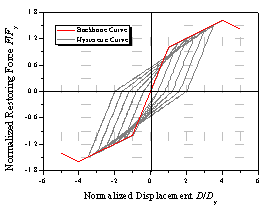
(a) g=+¡Þ
|
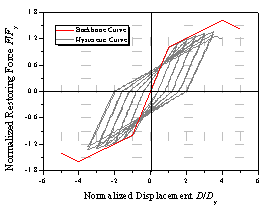
(b) g=100
|
|
|

|
|
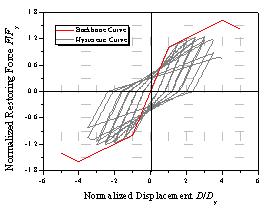
(c) g=50
|
(d) g=25
|
|
Figure 2 Hysteretic
curves for various g values
|
|
|
|
Figure 3 Simulation of the P-D effect
|
|
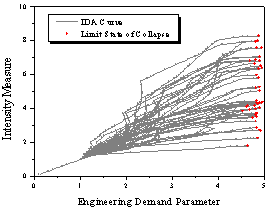
|
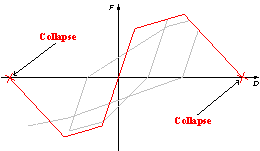
|
|
(a) Dynamic
pushover curve
|
(b) Dynamic
instability
|
|
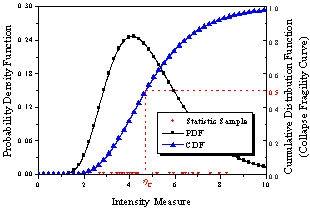
|
|
(c) Distribution
of collapse capacity
|
|
Figure 4 Collapse capacity
assessment of SDOF systems
|
|
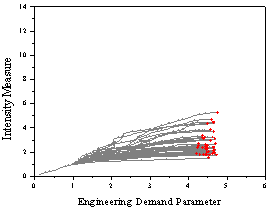
|
|
|
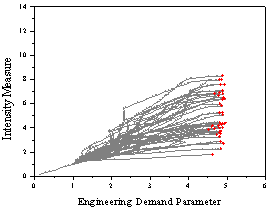
(a) T1=0.2 s
|
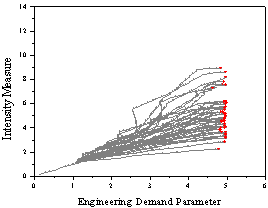
(b) T1=2.0 s
|
|
|
|
|
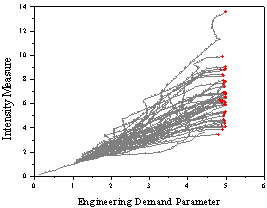
(c) T1=4.0 s
|
(d) T1=6.0 s
|
|
Figure 5 Dynamic
pushover curves for SDOF systems with various fundamental periods
|
|
|
|
Figure 6 Collapse
Capacity Spectrum
|
|
|
|
|
(a) Median
collapse capacity
|
(b) Dispersion
due to RTR uncertainty
|
|
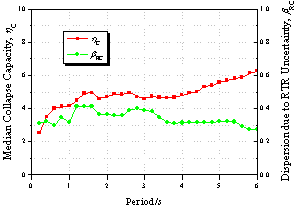
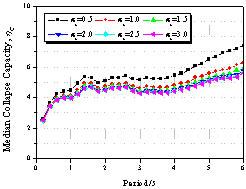
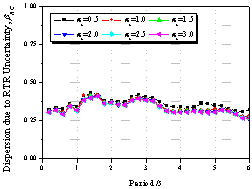
Figure 8 Influence
of the softening ratio ac
on collapse capacity spectrum
(as=0.00,
m=4.0, kf=1.0, g=Infinity,
q=0.00)
|
|
|
|
|
(a) kd=1.0
|
|
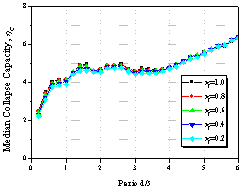
|
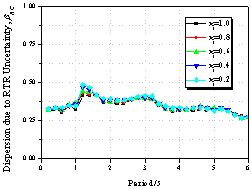
|
|
(b) kd=0.5
|
|
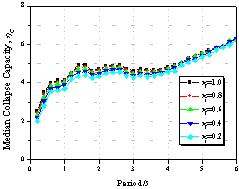
|
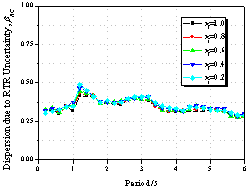
|
|
(c) kd=0.0
|
|
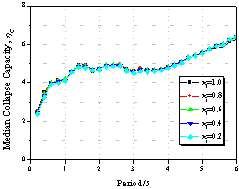
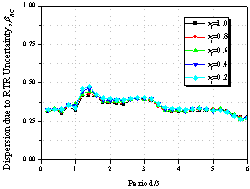
Figure 9 Influence
of the pinching property on collapse capacity spectrum
(as=0.00,
m=4.0, ac=1.0,
g=Infinity,
q=0.00)
|
|
|
|
|
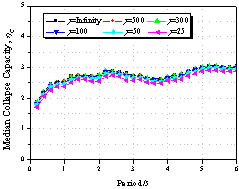
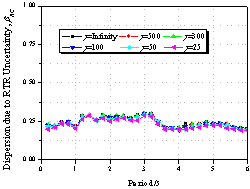
(a) m=2.0
|
|
|

|
|
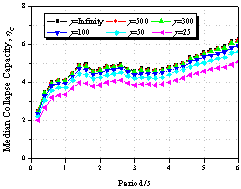
(b) m=4.0
|
|
|
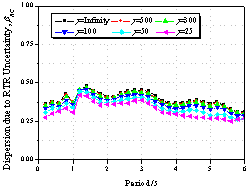
|
|
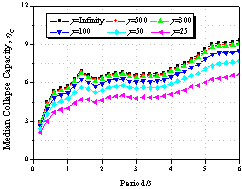
(c) m=6.0
|
|
Figure 10 Effect
of the cyclic deterioration property on collapse capacity spectrum
(as=0.00,
ac=1.0,
kf=1.0,
q=0.00)
|
|
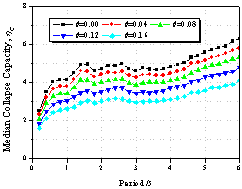
|
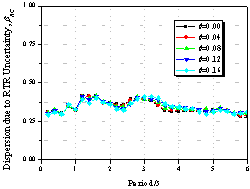
|
|
Figure 11 Effect of the P-D Effect on collapse capacity spectrum
(as=0.00, m =4.0, ac=1.0,
kf=1.0,
g=Infinity)
|
|
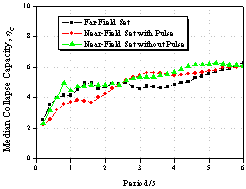
|
|
|
Figure 12 Collapse
capacity spectrum with different ground motion input
|
|