An Improved Ground Motion Intensity Measure for Super High-Rise Buildings

LU Xiao1, YE LiePing1, LU XinZheng1*, LI Mengke1 & MA Xiaowei1

1 Department of Civil Engineering, Tsinghua University, Beijing 100084, China;

Science China Technological Sciences, 2013, 56(6): 1525–1533. 

Download Full Text

Ground motion intensity measure (IM) is an important part in performance-based seismic design. A reasonable and efficient IM can make the prediction of the structural seismic responses more accurate. Therefore, a more reasonable IM for super high-rise buildings is proposed in this paper. This IM takes into account the significant characteristic that higher-order vibration modes play important roles in the seismic response of super high-rise buildings, as well as the advantages of some existing IMs. The key parameter of the proposed IM is calibrated using a series of time-history analyses. The collapse simulations of two super high-rise buildings are used to discuss the suitability of the proposed IM and some other existing IMs. The results indicate that the proposed IM yields a smaller coefficient of variation for the critical collapse status than other existing IMs and performs well in reflecting the contribution of higher-order vibration modes to the structural response. Hence, the proposed IM is more applicable to seismic design for super high-rise buildings than other IMs.

ground motion intensity measure, super high-rise building, time-history analysis, collapse analysis

DOI:10.1007/s11431-013-5234-1

If you need the PDF version of this paper, please email to luxinzheng@sina.com

1  Introduction

Performance-based seismic design has been widely adopted in structural seismic design since the Loma Prieta Earthquake in 1989 and the Northridge Earthquake in 1994[ 1 ]. The ground motion intensity measure (IM) is an important component of performance-based seismic design, which connects the seismic response of structures to the seismic hazard. A reasonable IM could effectively reduce the deviations in the prediction of the structural responses. Many studies on IMs for the conventional structures have been conducted in recent decades [2 -6 ].

In the early days, a single-parameter scalar intensity measure, such as the peak ground acceleration (PGA) or peak ground velocity (PGV), was widely used; later, spectral acceleration at the fundamental period Sa(T1) became widely adopted in the structural seismic design. Some studies [7 , 8 ] indicate that the spectral acceleration at fundamental period Sa(T1) can effectively reduce the deviation in prediction results of the structural seismic responses for the fundamental period-dominated structures. However, the deviation of Sa(T1) is still obvious if nonlinear behavior or the contribution of higher-order vibration modes is significant in the structural seismic responses [9 ]. Therefore, progress has been made in addressing these limitations. For example, Tothong and Luco [3 ] proposed the inelastic spectral displacement Sdi as the basic IM. The Sdi is computed from an equivalent single-degree-freedom system that has the same elastic period as the fundamental period of the designed structure. Based on the spectral acceleration at the fundamental period and the spectral acceleration at the inelastic period, and considering the structural period elongation in the nonlinear stage, Cordova et al.[4 ] proposed a combined intensity measure to consider the period elongation effect. Luco and Cornell [5 ] proposed an intensity measure, called IM1E&2E based on the first two vibration modes and the square-root-of-sum-of- squares (SRSS) rule of modal combination, to consider the impulse of the near-field ground motion. They also improved IM1E&2E and defined a new intensity measure named IM1I&2E, where the inelastic spectral displacement was adopted as a replacement for the elastic spectral displacement. Furthermore, Baker and Cornell [6 ] proposed a two-parameter vector intensity measure <Sa(T1), e > to solve these problems.

Since the completion of Taipei 101 in 2004, the first super high-rise building exceeding 500 m, the construction of super high-rise buildings is booming around the world, especially in China. Data from the Council on Tall Buildings and Urban Habitat (CTBUH) in 2012 indicates that before 2000, the average height of the first 20 tallest buildings in the world was approximately 375 m; but by 2010, the average height had increased to 439 m. Amazingly, the average height of the first 20 tallest super high-rise buildings is projected to reach 598 m by 2020. The fundamental periods of these super high-rise buildings are much longer than those of ordinary frame structures or shear wall structures. For example, the fundamental periods of Shanghai Tower [10 ] and Ping-An Finance Center [11 ], two super high-rise buildings under construction in China, will be larger than 9 s, which is far beyond the limit of 6 s specified in the design acceleration spectrum in the Chinese Code for Seismic Design of Buildings (GB50011-2010). Though great progress has been made on reducing the deviation of the prediction results of the structural seismic responses with reasonable IMs, it should be noted that most of these intensity measures are based on the ordinary structures with periods in the range of 0~4 s. Given the large number of super high-rise buildings that have been and will be constructed, the suitability of these intensity measures must be validated, and if necessary, a suitable and practical intensity measure for super high-rise buildings must be developed.

Therefore, based on the deformation characteristic of super high-rise buildings, as well as the advantages of the existing IMs, a practical and efficient intensity measure is proposed in this work using a simplified equivalent continuum model consisting of a flexural and a shear cantilever beam. The key parameter of the proposed intensity measure is calibrated by a series of time-history analyses, and a reasonable value is suggested. Collapse simulations of two super high-rise buildings are used to discuss the suitability of the proposed IM and other IMs for super high-rise buildings.

2  Analytical model and ground motion records

2.1 Analytical model

Two hybrid lateral force resisting systems, referred to as the “core tube/mega column/outrigger” and the “core tube/mega column/mega brace”, have been widely adopted for both completed super high-rise buildings and the ones under construction. The deformation mode of these structural systems is typically a combination of flexure and shear, which differs greatly from the deformation mode for the ordinary frame or shear wall structures. Though a refined finite element (FE) model for super high-rise buildings performs well in predicting and evaluating the seismic responses [10 -12 ], the number of the elements required is very large and the computational workload is very heavy, which makes the refined FE model inconvenient for parametric analysis on a large scale. This study focuses on the general rules of structures, therefore, an equivalent continuum model consisting of a flexural and a shear cantilever beam, proposed by Miranda and Taghavi [13 ], is adopted as a simplified model for super high-rise buildings (as shown in Figure 1). The flexural and shear cantilever beams are connected by an infinite number of axially rigid links to achieve the lateral deformation compatibility at the same story height. The response of this continuum model, subject to horizontal ground motion acceleration, is given by the following partial differential equation:

(1)

where r(x) denotes the mass per unit length in the model; u(x,t) is the lateral displacement at a non-dimensional height x at time t; x varies between 0 at the base of the building and 1 at the roof level; H is the total height of the building; ug(t) is the acceleration history of the ground motion; and EI(x) and GA(x) are the flexural stiffness of the flexural beam and the shear stiffness of the shear beam along the structural height, respectively. Miranda and Taghavi [13 ] assumed that the variations in the shear and flexural stiffness along the height are identical, i.e., EI(x)=EI0(x)S(x)，GA(x)=GA0S(x). EI0 and GA0 are the flexural and shear stiffness at the base of the model, respectively. S(x) is the dimensionless function that defines the variation of stiffness along the height of the simplified model.

The dimensionless parameter a0=H(GA0/EI0)1/2 controls the proportions of the flexural and shear deformations in the simplified model and thus the lateral deformation shape of the building. Miranda and Taghavi [13 ] suggested that a0 is normally between 0 and 1.5 for shear wall and braced-frame buildings; between 1.5 and 5 for buildings with dual structural systems consisting of a combination of moment-resisting frames and shear walls or a combination of moment-resisting frames and braced frames; and between 5 and 20 for moment-resisting frame buildings. In addition, when a0≥30, the deformation mode is dominated by shear deformations. Furthermore, Lu et al. [14 ] indicated that a0 is approximately 4.0 for Shanghai Tower with the total height of 632 m. And with this a0 value, the simplified model in Figure 1 can accurately represent the dynamic characters of Shanghai Tower when comparing to the refined FE model [14 ]. Therefore, based on a0=4.0, a series of simplified models with different fundamental periods, including the fundamental periods equal to 1, 2, 3, 4, 6, 8, 9 and 10 s, are obtained by changing the other parameters of the model, i.e., r(x) and EI0. These eight different simplified models are used in the following discussion.

Figure 1 Simplified model proposed by Miranda and Taghavi [13 ]

2.2  Ground motion records

Due to significant randomness in the ground motion records, structural responses may vary significantly in a time-history analysis. To minimize this variation while maintaining inherent randomness of the ground motions, 22 pairs of far-field ground motion records recommended by the FEMA P695 [15 ] are adopted in this study as the ground motion record set. The event magnitudes range from M6.5 to M7.6. The PGA values of this far-field ground motion record set vary from 210 gal to 820 gal, with an average value of 430 gal. The PGV values vary from 0.19 m/s to 1.15 m/s, with an average value of 0.46 m/s. Each pair of ground motion records includes two horizontal components and one vertical component. Only the two horizontal components of each ground motion are considered in this research, resulting in 44 natural records. Their corresponding elastic acceleration spectrums, with a 5% damping ratio, are shown in Figure 2. This ground motion record set not only maintains the randomness of the ground motions themselves but also leads to a certain degree of consistency in the structural responses.

Figure 2 Elastic response spectra of the 44 individual ground motions and media and one standard deviation response spectra of total record set

3  An improved ground motion intensity measure

Compared with the ordinary structures, a significant characteristic of super high-rise buildings is that the fundamental periods are very long and the higher-order vibration modes play important roles in their seismic responses. The failure modes may even be controlled by the higher-order vibration modes [16 ]. Hence, a preferable intensity measure for super high-rise buildings should consider the contribution of the higher-order vibration modes to structural seismic responses. Simultaneously, as a reasonable intensity measure, it has to be easy to use so that it can be widely accepted by engineers. Not only because the seismic design method in most design codes is based on the acceleration spectrum but also because most existing attenuation relations for seismic hazard are developed on the basis of spectral acceleration, the spectral acceleration Sa will be adopted in this study as the basic parameter used in the proposed IM. Because super high-rise buildings are so important, they are well designed with the performance-based design method and have sufficient safety margins to meet the performance demand subjected to the Maximum Considered Earthquake [LX1]   (MCE) specified in the design codes [12 ,17 ]. Thus, the main lateral force resisting components remain elastic or exhibit slight yielding when subjected to MCE rather than exhibit obvious nonlinear behavior. According to the above considerations, the fundamental period elongation is not considered in the proposed intensity measure. The improved ground motion intensity measure for super high-rise buildings can be expressed in the following general form:

(2)

where Sa(Ti) is the spectral acceleration for the ith period. n, the number of the translational vibrations modes to be concerned, is a parameter related to the structural fundamental period to be calibrated. S(__)a represents the improved IM. It reflects the geometric mean of the spectral acceleration at the first n periods of the structure, which contributes most to the structural seismic responses. For a given structure, the improved intensity measure can be obtained from the acceleration spectrum and it has closely related to the commonly used intensity measure Sa(T1). That is, when the fundamental period is very short, the value of n is equal to 1; the improve intensity measure will degenerate into the spectral acceleration at the fundamental period Sa(T1).

In application of the improved intensity measure S(__)a, the key issue is to determine an appropriate value of n that reflects the contribution of higher-order vibration modes to the seismic responses. This study suggests a reasonable value of n corresponding to the different fundamental periods with a series of time-history analysis. One original purpose of improving IM is to reduce the deviation of the prediction of the structural response. Many studies have indicated that among the existing structural demand measures, the maximum story drift ratio correlates best with structural damage [18 ]. Hence, the maximum story drift ratio is selected in this research as the basic structural demand measure to calibrate n. Many studies have also indicated [6 , 19 ] that the lognormal probability distribution is suitable for representing the predicted maximum story drift ratio. That is to say, the natural logarithms of the qmax (ln qmax) follow normal distribution. Hence, both the mean value and the standard deviation of the ln qmax, which are important parameters in probabilistic seismic demand analysis [20 ], can be calculated respectively as

(3)

(4)

Therefore, the value of n, which contributes to the minimum standard deviation of ln(qmax), is suggested as the reasonable n for the improved intensity measure. The steps for determining n are listed as follows:

(1) For a given structure with the fundamental period T1, determine trial values of n (n=1, 2, ……, 10).

(2) For each trial value of n, scale the 44 ground motion records by S(__)a and obtain the structural maximum story drift ratio qmax using time-history analysis.

(3) Calculate the standard deviation of ln(qmax) corresponding to each trial value of n and then select the optimal value of n for fundamental period T1 with the minimum standard deviation.

(4) Change the fundamental periods, repeat the above steps, and obtain a series of optimal values of n for different fundamental periods of T1. The relationship between n and T1 can be obtained by linear regression.

For the given trial values of n, the 44 ground motion records are scaled to the mean value of S(__)a. A series of time-history analysis of the simplified model with different fundamental periods mentioned in Section 2 is conducted. Some typical distributions of the standard deviation of ln(qmax) corresponding to different values of n and T1 are shown in Figure 3.


(a)     T1=1.0s

(b)     T1=2.0s

(c)      T1=3.0s

(d)     T1=8.0s

(e)     T1=9.0s

(f)      T1=10.0s

Figure 3 Distributions of sln(qmax) corresponding to different values of n

Obviously, when T1=1.0 s, the standard deviation of ln(qmax) increases with the increasing n, and ln(qmax) has the smallest standard deviation if n is equal to 1. At that point, S(__)a degenerates into the spectral acceleration at fundamental period Sa(T1). This conclusion, i.e., Sa(T1) can significantly reduce the deviation of the maximum story drift ratio for the fundamental period-dominated structures, has been demonstrated by other researchers [7 , 8 ]. Figure 3(b) indicates that when T1=2.0 s, n=2 will give the minimum standard deviation of ln(qmax). That is, S(__)a = [Sa(T1)∙Sa(T2)]1/2. When T1=3.0 s, Figure 3(c) shows that ln(qmax) has the smallest standard deviation when n=3. When T1=8 s, Figure 3(d) displays that ln(qmax) has the smallest standard deviation when n=4. Similarly, Figures 3(e) and (f) indicate that when T1=9.0 or 10.0 s, n=5 will yield the minimum standard deviation of ln(qmax). The distribution of optimal n corresponding to different fundamental periods of T1 is shown in Figure 4. Based on a linear regression of these discrete points, the relationship between n and T1 can be expressed by

(5)

The correlation coefficient R2 between n and T1 is approximately 0.91, which indicates that n and T1 are strongly correlated and Eq. (5) is a reasonable representation of the relationship between n and T1. When the fundamental period of the structure is not more than 1.0 s, Sa(T1) can be used directly as the IM, otherwise, the optimal value of n for different fundamental periods should be calculated with Eq. (5). The physical meaning of n requires that the value of n should be an integer; therefore, the value of n calculated using Eq. (5) should be rounded to the nearest integer to obtain the final value of n. For example, if the fundamental period of the structure is about 7.0 s, the optimal value of n is about 3.88 calculated from Eq. (5), and this value is rounded to the nearest integer to obtain a final value of 4 for n. In this case, the improved IM can be expressed as S(__)a = [Sa(T1)∙ Sa(T2)∙ Sa(T3) ∙Sa(T4)]1/4. Clearly, for super high-rise buildings, the standard deviation of ln(qmax) corresponding to S(__)a is much smaller than the standard deviation of ln(qmax) corresponding to Sa(T1). This improved IM can theoretically reflect the contribution of the higher-order vibration modes to the maximum story drift ratio.

Figure 4  Optimal values of n at different fundamental periods

4     Validation of the proposed intensity measure

In this section, collapse analysis based on incremental dynamic analysis (IDA) of the refined FE models of two super high-rise buildings are used to validate the feasibility of the proposed intensity measure. During the analysis, the 22 far-field ground motion records suggested in FEMA P695 [15 ] are selected as the basic seismic input, and the seismic intensities increase gradually until the structures collapse. Then, the critical ground motion intensities and the coefficient of variation of each intensity measure causing the structure to collapse are obtained and compared. The compared IMs are listed in Table 1. The smaller the coefficient of variation is, the more efficient the intensity measure is for super high-rise buildings.

Table 1  Ground motion intensity measures compared in this paper

Intensity measure

Description

Unit

PGA

The peak ground acceleration

g

PGV

The peak ground velocity

cm/s

PGD

The peak ground displacement

cm

Sa(T1)

The spectral acceleration at fundamental period

g

IM1E&2E

The intensity measure, proposed by Luco and Cornell [5 ], considers the contribution of higher-order vibration modes caused by the near-fault impulse.

  

S(__)a

The improved intensity measure proposed by this study

g

The refined FE models of the two super high-rise buildings discussed in this paper are shown in Figures 5 and 6. Model A represents the Shanghai Tower, with a total height of 632 m. The hybrid lateral force resisting system referred to as a “core tube/mega column/outrigger” system is adopted; its diagram is shown in Figure 5. The main part of the core tube is a 30 m×30 m square reinforced concrete (RC) tube with a maximum thickness of 1.2 m at the bottom. The mega column is made up of shaped-steel reinforced concrete with a maximum cross-sectional dimension of 5300 mm×3700 mm. The height of the outrigger is approximately 9.9 m. The fundamental period of Model A is approximately 9.0 s, and the optimal value of n is approximately 5, according to Eq. (5). Consequently, S(__)a can be expressed as S(__)a = [Sa(T1)∙Sa(T2)∙Sa(T3) Sa(T4) Sa(T5)]1/5.

Figure 5  FE model of Model A

Figure 6  FE model of Model B

Model B represents another super high-rise building, with a total height of 532 m. The hybrid lateral force-resisting system, referred to as a “core tube/mega column/mega brace”, is adopted in the lower four zones, while another hybrid lateral force-resisting system, referred to as a “core tube/mega column/outrigger”, is used in the upper four zones. A diagram of Model B is shown in Figure 6. As with Model B, the core tube is a 30 m×30 m square RC tube. The maximum thickness of the wall is approximately 1.1 m at the bottom. The mega column is a concrete-filled steel tube with a maximum cross section of approximately 6.5 m × 6.5 m. The thickness of the steel tube is 80 mm. The height of the outrigger is approximately 9.0 m. The mega brace is made up of welded steel box beams, with a maximum dimension of 1800 mm× 900 mm × 110 mm × 110 mm. The fundamental period of Model B is approximately 7.5 s, and the optimal n is approximately 4, as calculated using Eq. (5), resulting in S(__)a = [Sa(T1)∙Sa(T2)∙Sa(T3) Sa(T4)]1/4.

The refined FE models for the two super high-rise buildings are built up using the general finite element program of MSC.Marc 2007. In these two models, the shear wall is simulated by multi-layer shell elements that display outstanding nonlinear performance in replicating both in-plane and out-of-plane bending and shear coupling behaviors. The horizontal and vertical reinforcement in the wall is treated as the equivalent rebar layers along the thickness direction of the shell. The concentrated reinforcement in the boundary zones in the shear wall is simulated by beam elements that are incorporated into the shell element sharing the nodes. The outrigger, mega brace and secondary frame, which are constructed by H-shaped or box-shaped steel beams, are simulated by widely used fiber beam element model. The combined model, consisting of multi-layer shell and truss element, is adopted for the H-shaped steel reinforced mega columns in Model A. The parameters of the combined model are calibrated by the refined solid model of mega column under various load scenarios, including pure compression, pure bending, bending with compression in one direction and bending with biaxial compression. The details of the calibration were given by Lu et al. [21 ]. The structural components will lose their load carrying capacities gradually during the structural collapse. Elemental deactivation technology is adopted to simulate this phenomenon. The details of the collapse simulation and the hysteretic relationships between the strain and stress of key components were given by Lu et al. [16 ]. The accuracy and feasibility of this methodology to simulate the collapse of high-rise buildings have been validated in refs.[16 , 22 , 23 ]. During the IDA collapse analysis, the ground motion is inputted along the x direction and a Rayleigh damping with the value of 5% is adopted. The typical potential collapse modes of these two super high-rise buildings are shown in Figures 7 and 8. The coefficient of variation (COV) of the six different ground motion intensity measures corresponding to the two super high rise buildings are displayed in Figures 9 and 10 , respectively.

Figure 7 Potential typical collapse mode of Model A

Figure 8 Potential typical collapse mode of Model B

Figure 9 Distribution of COV of Model A corresponding to different ground motion intensity measures at the critical collapse status

Figure 10 Distribution of COV of Model B corresponding to different ground motion intensity measures at the critical collapse status

Figure 9 clearly indicates that among these different IMs used to represent the critical seismic intensities causing Model A to collapse, the coefficient of variation for S(__)a is the smallest with a value of only 0.207, which is only 37.5% of the coefficient of variation for Sa(T1). PGV also shows a smaller COV, which is approximately 0.249, or 45.1% of the coefficient of variation for Sa(T1). The coefficient of variation for Sa(T1) is the largest which demonstrates that considering the first vibration mode only does not reflect the seismic responses characteristics of super high-rise buildings. In contrast, intensity measure IM1E&2E considers the first two vibration modes, and its coefficient of variation is smaller than the value of Sa(T1) but larger than that of S(__)a. This means that considering only the first two orders of vibration modes does not adequately reflect the seismic response of super high-rise buildings either. According to Eq. (5), the contribution of higher-order vibration modes for Shanghai Tower can be better reflected when the first five translational vibration modes are considered. Consequently, the IM1E&2E is extended using the first five translational vibration modes and it is referred to as IM1E-5E in the following discussion. The comparison in Figure 9 indicates that IM1E-5E performs better than IM1E&2E and the coefficient of variation of IM1E-5E is about 0.218, which is the second smallest COV in these intensity measures, just a little larger than the value of S(__)a. The physical meaning of IM1E&2E or IM1E-5E is the mode superposition result of maximal story drift ratio using the first two or five vibration modes. Hence, the calculation of IM1E&2E or IM1E-5E is very complicated. However, the improved intensity measure S(__)a has a much simpler form and it’s easy and convenient for engineers to use. Similarly, Figure 10 shows that among the different IMs used to represent the critical seismic intensities that cause the collapse of Model B, the coefficient of variations for PGV and S(__)a are smaller than those for the other intensity measures. PGD and Sa(T1) have the highest coefficient of variation. Besides, the extended IM1E&2E using the first four vibration modes (IM1E-4E) according to Eq. (5) also performs better than IM1E&2E but not so good as PGV and S(__)a.

Overall, PGV and the improved intensity measure S(__)a are efficient in representing the critical seismic intensities that cause the collapse of super high-rise buildings. This finding is coincided with the statement by Lu et al. [24 ] that “PGV can be selected as the intensity measure for seismic response prediction and collapse analysis for super high-rise buildings”. However, when the fundamental period of the structure is short, according to Ye et al. [8 ], PGV does not correlate with the maximum story drift ratio as well as Sa(T1). Because the improved intensity measure S(__)a can degenerate into Sa(T1) for structures with short or median fundamental period, S(__)a has a wider applicability than PGV. Furthermore, it should be noted that the improved intensity measure S(__)a is proposed based on the spectral acceleration, so it is very convenient to use the design acceleration spectrum specified in the seismic design code directly, as well as the existing attenuation relations for probabilistic seismic hazard analysis. However, PGV does not offer this convenience. Therefore, the improved IM proposed in this paper is an efficient and practical intensity measure for seismic design of super high-rise buildings.

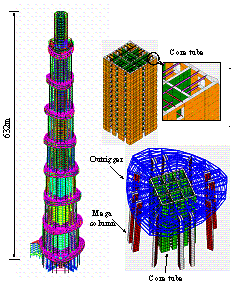
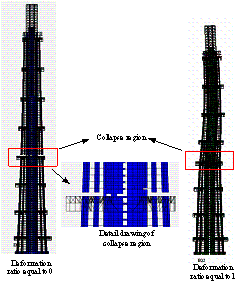
5  Conclusions

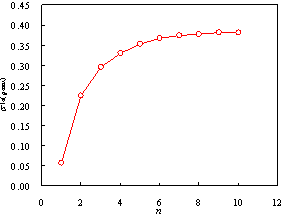
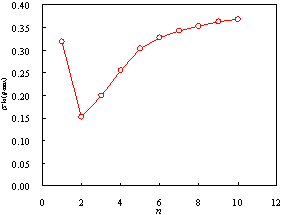
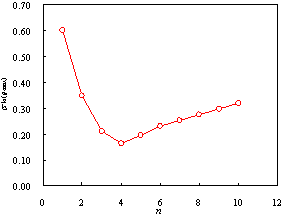
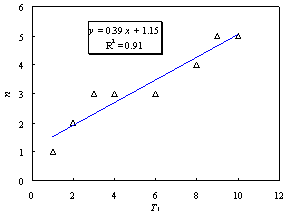
An IM for super high-rise buildings that is more accurate and practical than other existing intensity measures is proposed in this paper. This intensity measure takes into account the fact that higher-order vibration modes play important roles in the seismic response of super high-rise buildings, as the advantages of some existing IMs as well. The values for the key parameter in the improved intensity measure is determined by a series of time-history analysis with a simplified equivalent continuum model consisting of a flexural and a shear cantilever beam. The analysis indicates that the proposed formula for n reflects the contribution of higher-order vibration modes to the seismic responses for super high-rise buildings and can significantly reduce the deviation of the predicted seismic responses. Collapse simulations of two super high-rise buildings are used to demonstrate the suitability of the proposed intensity measure and some other existing intensity measures for super high-rise buildings. The results indicate that the proposed IM yields the smallest coefficient of variation among the considered IMs at the critical status of collapse. Moreover, the proposed intensity measure has greater applicability than other IMs and can be selected as the IM for seismic design and collapse analysis for super high-rise buildings.

It should be also noted that the above conclusion is obtained only based on the far-field ground motions suggested by FEMA P695[15]. Therefore, it’s necessary to use more ground motions like those with quite long fundamental period and the near-field ground motions to validate this conclusion in the future work.

 

Acknowledgement

This work was supported by “Twelfth Five-Year” plan major projects supported by National Science and Technology (Grant No. 2011BAJ09B01), the National Nature Science Foundation of China (Grant Nos. 51222804, 51261120377), the Tsinghua University Initiative Scientific Research Program (Grant Nos. 2012THZ02-2, 2011THZ03) and the Fok Ying Dong Education Foundation (Grant No. 131071).

   1         Hamburger R, Rojahn C, Moehle J, et al. The ATC-58 Project: Development of next-generation performance-based earthquake engineering design criteria for buildings, 13th World Conference on Earthquake Engineering, Vancouver, B.C., Canada, August 1-6, 2004, Paper No. 1819.

   2         Shome N，Cornell C A，Bazzurro P, et al. Earthquakes, records and nonlinear responses. Earthq Spectra, 1998, 14:469-500.

   3         Tothong P and Luco N. Probabilistic seismic demand analysis using advanced intensity measures. Earthquake Eng Struct Dyn, 2007, 36:1837-1860.

   4         Cordova P P, Deierlein G G, Mehanny S S F, et al. Development of a two-parameter seismic intensity measure and probabilistic assessment procedure. The Second U.S.-Japan Workshop on Performance-based Earthquake Engineering Methodology for Reinforced Concrete Building Structures, Sapporo, Japan, 2001, 187-206.

   5         Luco N and Cornell C A. Structure-specific scalar intensity measures for near-source and ordinary earthquake motions. Earthq Spectra, 2007, 23:357-391.

   6         Baker J W and Cornell C A. A vectored-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthquake Eng Struct Dyn, 2005, 34:1193-1217.

   7         Vamvatsikos D and Cornell C A. Incremental dynamic analysis. Earthquake Eng Struct Dyn, 2002, 31: 491-514.

   8         Ye L P, Ma Q L, Miao Z W, et al. Numerical and comparative study of earthquake intensity indices in seismic analysis, Struct Des Tall Spec, 2013, 22: 362-381.

   9         Lucchini A, Mollaioli F and Monti G. Intensity measures for response prediction of a torsional building subjected to bi-directional earthquake ground motion. B Earthq Eng, 2011, 9: 1499-1518.

10         Jiang H J, He L S, Lu X L, et al. Analysis of seismic performance and shaking table tests of the Shanghai Tower (in Chinese). J Building Structures, 2011, 32:55-63.

11         Yang X Q, Fu X Y and Huang Y J. Dynamic elasto-plastic analysis of the Shenzhen Ping’an Financial Center Tower (in Chinese). J Building Structures, 2011, 32:40-49.

12         Fan H, Li Q S, Alex Y T, et al. Seismic analysis of the world's tallest building. J Construct Steel Res, 2009, 65: 1206–1215.

13         Miranda E and Taghavi S. Approximate floor acceleration demands in multistory buildings I: Formulation. J Struct Eng-ASCE, 2005, 131:203-211.

14         Lu X, Lu X Z, Ye L P, et al. Collapse analysis of super high-rise building and discussion on the ground motion intensity measures. 15th World Conference on Earthquake Engineering, Lisbon, Portugal, September 24-28, 2012, Paper No. 0164.

15         FEMA, 2009, FEMA P695: Quantification of building seismic performance factors. Applied Technology Council, Redwood City, C.A., 2009.

16         Lu X, Lu X Z, Zhang W K, et al. Collapse simulation of a super high-rise building subjected to extremely strong earthquakes. Sci China Tech Sci, 2011, 54: 2549-2560.

17         Ding J M, Wu H L and Zhao X. Seismic performance analysis and evaluation of Shanghai Tower under Maximum Considered Earthquake (in Chinese). J Civil Architect Environ Eng, 2010, 32: 231–233.

18         Miranda E and Akkar S D. Generalized interstory drift spectrum. J Struct Eng-ASCE, 2006, 132: 840-852.

19         Miranda E and Aslani H. Probabilistic response assessment for building-specific loss estimation. PEER 2003/03, Pacific Earthquake Engineering Research Center, University of California at Berkeley, Berkeley, CA, 2003.

20         Shi W, Lu X Z, Ye L P. Uniform-risk-targeted seismic design for collapse safety of building structures. Sci China Tech Sci, 2012, 55: 1481-1488.

21         Lu X Z, Zhang W K, Lu X, et al. Elasto-plastic mechanical behavior of detailed finite element model and simplified model of mega columns (in Chinese). J Shenyang Jianzhu University (Natural of Science). 2011, 27: 409-417.

22         Lu X, Lu X Z, Guan H, et al. Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes, Earthquake Eng Struct Dyn, 2013, 42: 705-723.

23         Lu X Z, Lu X, Guan H, et al. Earthquake-induced collapse simulation of a super-tall mega-braced frame-core tube building, J Constr Steel Res, 2013, 82: 59–71.

24         Lu X, Lu X Z and Ye L P. Discussion on the ground motion intensity measures for super high-rise buildings (in Chinese). China Civil Eng J, 2012, 45: 292-296.


  [LX1] This is a technical term in seismic engineering.
Introduction
Research
Application
Teaching
Publications
Download
Issues
Others

 

Our Lab

Collapse Prevention Committee