6. CONCLUSIONS
From the experimental and numerical results presented in this
paper, the following three conclusions can be drawn:
(1) The shaking table test
results indicate that the test model suffers little
damage under the design level earthquake load (ground motion of PGA
= 0.4 g). It can also meet the collapse prevention requirements for severe
earthquakes (ground motion of PGA = 0.88 g). Therefore, the prototype structure
is able to satisfy the seismic performance demand of 7- degree seismic design
intensity.
(2) The displacement envelope of the mega-frame structure exhibits a shear dominated mode, and the
first vibration mode plays an important role in its dynamic response. After the installation
of TMD, the first vibration period is increased and the time-history displacement
is reduced, suggesting that the TMD can be used for effective vibration control
for super tall mega-frame buildings.
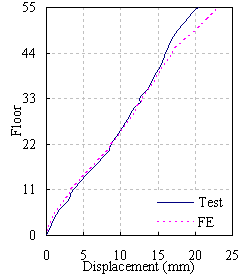
(3) The FE results agree well with test data which confirms the accuracy of the FE analysis. The
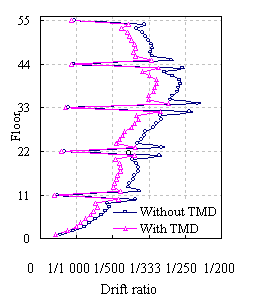
FE results demonstrate that the inter-story drifts at the mega-beam stories are much smaller than those at
the adjacent stories (i.e., MBS-D and MBS-U), which significantly reduce the
cumulative inter-story drift of the structure. However, the inter-storey drifts of MBS-U and MBS-D stories are obviously larger than
those of the other stories, which should be designed with special strengthening
scheme.
Upon verification of the FE model, the damage mechanism, collapse resistance
and parameter optimization of TMD, which cannot be readily identified in the
laboratory test, will be further studied
in the future. The outcomes can be directly used to guide the design of mega-frame
structures alike.
ACKNOWLEDGEMENT
The authors are grateful for the financial support received from the National
Nature Science Foundation of China (No. 51222804, 91315301, 51261120377),
the Fok Ying Dong Education Foundation (No. 131071) and the State Key Laboratory
for Disaster Reduction in Civil Engineering Foundation (SLDRCE08-HZ-01).
Ali
MM, Moon KS. 2007. Structural developments in tall buildings:
current trends and future prospects. Architectural Science Review.
50(3): 205-223.
China Ministry of Construction.
2010. Code for Seismic
Design of Buildings (GB50011-2010). China Architecture and Building Press: Beijing, China (English
edn).
China Ministry of Construction. 2002. Technical Specification for
Concrete Structures of Tall Building (JGJ3-2002). China Architecture and Building Press: Beijing, China
(in Chinese).
Den
Hartog JP. 1956. Mechanical
Vibration, 4th edn. McGraw-Hill: New York, USA.
Feng MQ, Mita A. 1995. Vibration control of tall buildings
using mega subconfiguration.
Journal of Engineering Mechanics. 121 (10): 1082-1088.
Ghorbani-Tanha
AK, Noorzad A, Rahimian M. 2009. Mitigation of wind-induced
motion of Milad Tower by tuned mass damper. The Structural Design
of Tall and Special Buildings. 18(4): 371–385.
Ghosh A, Basu B.
2007. A closed-form optimal tuning criterion for TMD in damped structures.
Structural Control and Health Monitoring. 14(4): 681–692.
Irwin
P, Kilpatrick J, Robinson J, et al. 2008. Wind and tall buildings: negatives
and positives. The Structural Design of Tall and Special Buildings.
17(5): 915-928.
Khan FR. 1969. Recent
structural systems in steel for high-rise buildings. In Proceedings
of the British Constructional Steelwork Association Conference on Steel in
Architecture. London: British Constructional Steelwork Association.
Khan FR. 1972. Influence
of design criteria on selection of structural systems for tall buildings,
In Proceedings of the Canadian Structural Engineering Conference. Toronto:
Canadian Steel Industries Construction Council,1-15.
Khan FR. 1973. Evolution
of structural systems for high-rise buildings in steel and concrete. In
J. Kozak (Ed.), Tall Buildings in the Middle and East Europe: Proceedings
of the 10th Regional Conference on Tall Buildings-Planning.
Design and Construction. Bratislava: Czechoslovak Scientific and Technical
Association.
Kim
J, Jung M. 2013. Progressive collapse-resisting capacity of modular mega-frame
buildings. The Structural Design of Tall and Special Buildings.
22(6): 471-484.
Kim YM, You KP, Kim HY. 2008.
Wind-induced excitation control of a tall building with tuned mass dampers.
The Structural Design of Tall and Special Buildings. 17(3): 669–682.
Ko DW, Lee
HS. 2006, Shaking table tests on a high-rise RC building model having
torsional eccentricity in soft lower storeys. Earthquake
Engineering & Structural Dynamics. 35(11):1425–1451.
Kourakis I. 2007. Structural systems and tuned mass dampers of super-tall buildings:
case study of Taipei 101. Doctoral dissertation, Massachusetts
Institute of Technology, Cambridge, USA
Kwok KCS, Macdonald PA. 1990. Full-scale measurement of wind-include acceleration
response of Sydney Tower. Engineering
Structures. 12(3): 153-162.
Lan ZJ, Tian YJ, Fang L, Liang
ST, Wang X.D. 2004. An experimental study on seismic
responses of multifunctional vibration-absorption reinforced concrete megaframe
structures. Earthquake Engineering & Structural Dynamics.
33(1): 11–14.
Li CS,
Lam SS, Zhang MZ, Wong YL. 2006, Shaking table test of a 1:20 scale high-rise
building with a transfer plate system. Journal of Structural Engineering.
132(11): 1732–1744.
Lu X, Lu XZ, Guan H, Ye LP. 2013. Collapse simulation of reinforced concrete
high-rise building induced by extreme earthquakes, Earthquake
Engineering & Structural Dynamics. 42(5): 705-723.
Lu X, Chen J. 2011. Mitigation
of wind‐induced response of Shanghai Center Tower by tuned mass damper. The Structural
Design of Tall and Special Buildings. 20(4): 435-452.
Lu XL, Chen Y, Mao YJ. 2012b. Shaking table model test and numerical analysis of a
supertall building with high-level transfer storey. The Structural
Design of Tall and Special Buildings. 21(10): 699-723.
Lu XL, Li P, Guo X, Shi W, Liu J.
2012a. Vibration control using ATMD and site measurements on
the Shanghai World Financial Center Tower. The Structural Design of Tall
and Special Buildings. Doi: 10.1002/tal.1027
Lu
XL. 2007, Seismic
Theory and Application of Complex High-Rise Building Structure. Science
Press: Beijing, China (in Chinese).
Miao ZW, Ye LP, Guan H, Lu XZ. 2011. Evaluation
of modal and traditional pushover analyses in frame-shear-wall structures,
Advances in Structural Engineering. 14(5): 815-836.
Ohtake K, Mataki Y, Ohkuma T, Kanda J, Kitamura H. 1992. Full-scale
measurements of wind actions on Chiba Port Tower. Journal of Wind Engineering
and Industrial Aerodynamics. 43(1): 2225–2236.
Sabnis GM, Harris HG, White RN, Mirza MS. 1983. Structural Modeling and Experimental
Techniques. Prentice-Hall: Engle-wood Cliffs, NJ USA.
Sadek
F, Mohraz B, Taylor AW, Chung RM. 1997. A method of estimating the parameters
of tuned mass dampers for seismic applications. Earthquake Engineering
and Structural Dynamics. 26(6): 617-635.
Shu GP, Zhang YF, Lu ZT, Zuo
J, Xia CC, Jiang H. 2005. The aseismic capability and shaking table experiment
of mega-frame structures. SISS 2005: Innovation & Sustainability of
Structures. 1-3: 398-414.
Taranath BS. 1997. Steel,
Concrete, and Composite Design of Tall Buildings, McGraw Hill: New
York, NY.
Wang DC. 2010. Research on
energy spectrum and the selection of earthquake accelerograms for dynamic
analysis based on energy. Doctoral dissertation, Hefei University of Technology,
Hefei, China (in Chinese).
Zhang XA, Zhang JL, Wang D, Jiang
JS. 2005. Controlling characteristic of passive mega-subcontrolled
frame subjected to random wind loads. Journal of Engineering Mechanics
131(10): 1046-1055.
Zhou FL.
1997. Engineering structural vibration control. Seismological Press:
Beijing, China (in Chinese).
Zuo
L, Nayfeh SA. 2005. Optimization
of the individual stiffness and damping parameters in multiple–tuned–mass-damper
systems. Transactions of the ASME-L-Journal
of Vibration and Acoustics. 127(1): 77–83.
List
of Tables
Table 1 Scaling factors
Table 2 Weights of
iron blocks on different floors
Table 3 Test procedure
Table 4 The first four vibration periods of the test model
Table 5. Elements used to model the structural components
Table 6 Experimental and FE analytical vibration periods
List of Figures
Figure 1 Structural
layout of the mega-frame
Figure 2 Three-dimensional view of a typical
mega-beam story
Figure 3 Plan layout of a typical substructure story (units: mm)
Figure 4 Photo of the shaking table model
Figure 5. The installation
of TMD
Figure 6. Artificial accelerogram
Figure 7 Elastic modal shapes in X direction without TMD
Figure 8 Elastic modal shapes in X direction with TMD
Figure 9 Fourier spectrums at the top of the model with and without
TMD subjected to white noise
Figure 10 Displacement envelope in X direction under El-Centro ground
motion
Figure 11 Displacement envelope in X direction under artificial accelerogram
Figure 12 Displacement envelope in X direction under other ground motions
Figure 13 Displacement envelope in X direction of load case EX3 and EY3
Figure 14 Lateral displacement responses under El-Centro ground motion
of 0.88g
Figure 15 The FE model
Figure 16 Displacement envelope under El Centro ground motion of 0.88g
Figure 17 Inter-story drifts under El Centro ground motion of 0.88g
Table 1 Scaling factors
| |
Design parameter
|
Expression
|
Scaling factor
|
|
Material
|
Strain, ε
|
Sε
|
1
|
|
Stress, σ
|
Ss
|
0.35
|
|
Elastic modulus, E
|
SE
|
0.35
|
|
Density, ρ
|
Sr=
Ss/Sa·Sl
|
2.118
|
|
Mass, m
|
Sm= Ss Sl2/ Sa
|
0.00014
|
|
Geometrical
|
Length, l
|
Sl
|
0.04
|
|
Area, A
|
SA=
Sl2
|
0.0016
|
|
Translational displacement X
|
SX=
Sl
|
0.04
|
|
Angular displacement β
|
Sβ
|
1
|
|
Load
|
Concentrated load, F
|
SF=SsSl2
|
0.00032
|
|
Area load p
|
Sp=Ss
|
0.20
|
|
Dynamic
|
Stiffness, k
|
Sk=SESl
|
0.014
|
|
Period, T
|
ST=Sl0.5·Sa-0.5
|
0.1
|
|
Frequency, f
|
Sf=Sl-0.5·Sa0.5
|
10
|
|
Damping, c
|
Sc=Ss·Sl1.5·Sa-0.5
|
0.0014
|
|
Velocity, v
|
Sv=(Sl-·Sa)0.5
|
0.118
|
|
Acceleration, a
|
Sa
|
4
|
|
Acceleration of gravity, g
|
Sg
|
1
|
Table 2 Weights
of iron blocks on different floors
|
Substructure
|
MBS-D
|
MBS
|
|
Floor
|
Weight
(kg)
|
Floor
|
Weight
(kg)
|
Floor
|
Weight
(kg)
|
|
1-9,12-13
|
172
|
10
|
205
|
11
|
253
|
|
14-20,23-24
|
161
|
21
|
194
|
22
|
240
|
|
25-31,34-35
|
151
|
32
|
184
|
33
|
228
|
|
36-42
|
140
|
43
|
173
|
44
|
215
|
|
45-53
|
140
|
54
|
173
|
55
|
234
|
Table 3 Test procedure
|
Case
designation
|
Input excitation
|
With/without TMD
|
Directions
|
Design peak value of input acceleration (g)
|
Actual peak value of input acceleration (g)
|
|
X
|
Y
|
Z
|
X
|
Y
|
Z
|
|
WN1
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX1
|
El-Centro
|
Locked
|
X
|
0.14
|
-
|
-
|
0.136
|
-
|
-
|
|
RX1
|
Artificial
|
Locked
|
X
|
0.14
|
-
|
-
|
0.181
|
-
|
-
|
|
EZ1
|
El-Centro
|
Locked
|
X+Y+Z
|
0.14
|
0.119
|
0.119
|
0.13
|
0.23
|
0.04
|
|
WN1-D
|
White noise
|
Active
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX1-D
|
El-Centro
|
Active
|
X
|
0.14
|
-
|
-
|
0.143
|
-
|
-
|
|
RX1-D
|
Artificial
|
Active
|
X
|
0.14
|
-
|
-
|
0.165
|
-
|
-
|
|
WN2
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX2
|
El-Centro
|
Locked
|
X
|
0.28
|
-
|
-
|
0.321
|
-
|
-
|
|
RX2
|
Artificial
|
Locked
|
X
|
0.28
|
-
|
-
|
0.376
|
-
|
-
|
|
EY2
|
El-Centro
|
Locked
|
X+Y
|
0.28
|
0.238
|
-
|
0.31
|
0.31
|
-
|
|
EX2-D
|
El-Centro
|
Active
|
X
|
0.28
|
-
|
-
|
0.332
|
-
|
-
|
|
RX2-D
|
Artificial
|
Active
|
X
|
0.28
|
-
|
-
|
0.374
|
-
|
-
|
|
WN3
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX3
|
El-Centro
|
Locked
|
X
|
0.4
|
-
|
-
|
0.426
|
-
|
-
|
|
RX3
|
Artificial
|
Locked
|
X
|
0.4
|
-
|
-
|
0.409
|
-
|
-
|
|
EY3
|
El-Centro
|
Locked
|
X+Y
|
0.4
|
0.34
|
-
|
0.42
|
0.41
|
-
|
|
EX3-D
|
El-Centro
|
Active
|
X
|
0.4
|
-
|
-
|
0.426
|
-
|
-
|
|
RX3-D
|
Artificial
|
Active
|
X
|
0.4
|
-
|
-
|
0.408
|
-
|
-
|
|
WN4
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX4-D
|
El-Centro
|
Active
|
X
|
0.88
|
-
|
-
|
1.093
|
-
|
-
|
|
RX4-D
|
Artificial
|
Active
|
X
|
0.88
|
-
|
-
|
0.828
|
-
|
-
|
|
EX4
|
El-Centro
|
Locked
|
X
|
0.88
|
-
|
-
|
0.932
|
-
|
-
|
|
WN5
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
CCX5-D
|
Chi-Chi
|
Active
|
X
|
0.88
|
-
|
-
|
1.014
|
-
|
-
|
|
WN6
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
|
EX6
|
El-Centro
|
Locked
|
X
|
1.2
|
-
|
-
|
1.222
|
-
|
-
|
|
CCX6
|
Chi-Chi
|
Locked
|
X
|
1.2
|
-
|
-
|
0.832
|
-
|
-
|
|
WX6-1
|
Wenchuan
|
Locked
|
X
|
0.4
|
-
|
-
|
0.473
|
-
|
-
|
|
WX6-2
|
Wenchuan
|
Locked
|
X
|
0.88
|
-
|
-
|
0.875
|
-
|
-
|
|
WX6-3
|
Wenchuan
|
Locked
|
X
|
1.2
|
-
|
-
|
1.147
|
-
|
-
|
|
WN7
|
White noise
|
Locked
|
X+Y+Z
|
0.07
|
0.07
|
0.07
|
-
|
-
|
-
|
Table 4 The first four vibration periods
of the test model
|
Case
designation
|
Vibration periods
in X direction
(s)
|
Vibration periods in Y direction (s)
|
|
First mode
|
Second mode
|
Third mode
|
Fourth
mode
|
First mode
|
Second mode
|
Third mode
|
Fourth mode
|
|
1WN
|
0.510
|
0.158
|
0.074
|
0.045
|
0.513
|
0.147
|
0.070
|
0.043
|
|
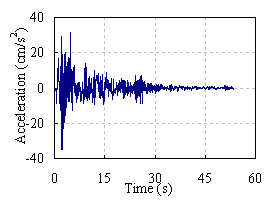
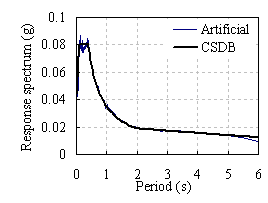
1WN –D
|
0.583
|
0.146
|
0.074
|
0.046
|
0.525
|
0.160
|
0.070
|
0.043
|
|
2WN
|
0.544
|
0.155
|
0.076
|
0.046
|
0.528
|
0.160
|
0.071
|
0.043
|
|
3WN
|
0.583
|
0.158
|
0.079
|
0.048
|
0.562
|
0.160
|
0.071
|
0.044
|
|
4WN
|
0.583
|
0.169
|
0.082
|
0.049
|
0.575
|
0.160
|
0.073
|
0.043
|
|
5WN
|
0.702
|
0.186
|
0.089
|
0.055
|
0.581
|
0.159
|
0.076
|
0.046
|
|
6WN
|
0.833
|
0.243
|
0.110
|
0.064
|
0.595
|
0.190
|
0.082
|
0.051
|
|
7WN
|
0.963
|
0.243
|
0.108
|
0.067
|
0.620
|
0.192
|
0.085
|
0.054
|
Table 5. Elements used
to model the structural components
|
Element type
|
Structural components
|
|
Spatial
beam elements
|
Beam and columns in the substructure and
mega-beams
|
|
Truss
elements
|
Rebar embedded in shear walls
|
|
Thin-walled
section beam elements
|
Shaped steel embedded at the boundary
of the shear walls
|
|
Multi-layer
shell elements
|
Shear walls, coupling beams and floor
slabs
|
|
Springs
elements
|
Springs and dampers of TMD
|
Table 6 Experimental and
FE analytical vibration periods
|
Period (s)
|
Test model
|
FE model
|
|
First mode
|
0.510
|
0.509
|
|
Second mode
|
0.158
|
0.152
|
|
Third mode
|
0.074
|
0.075
|
|
Fourth mode
|
0.045
|
0.046
|
  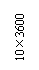  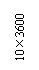 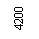 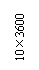     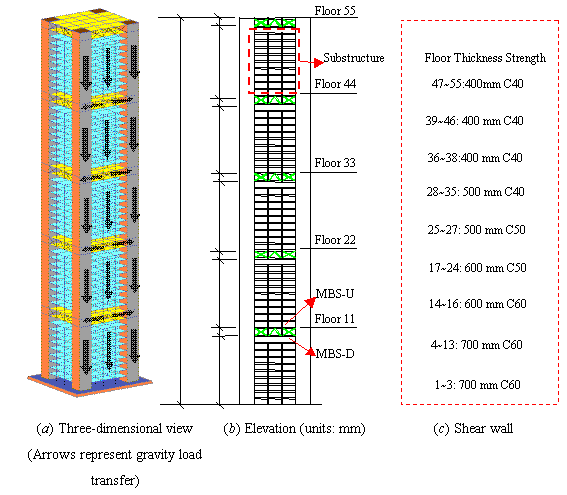

Figure 1 Structural layout of the mega-frame
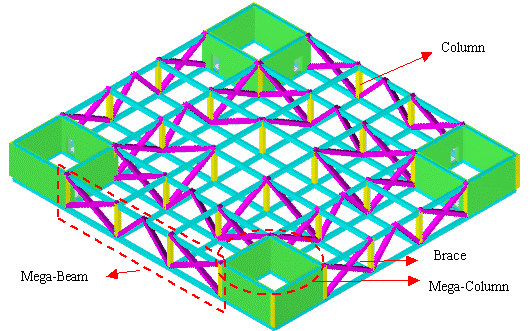

Figure 2 Three-dimensional view of a typical mega-beam story

Figure 3 Plan layout of a typical
substructure story (units: mm)


Figure 4 Photo of
the shaking table model

Figure 5
The installation of TMD
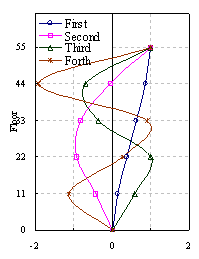
Figure 7 Elastic modal shapes in X direction without TMD
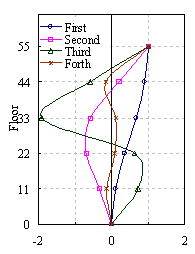
Figure 8 Elastic modal shapes in X direction with TMD
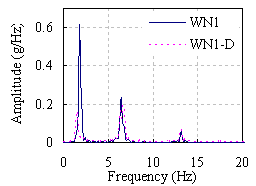
Figure 9 Fourier spectrums at the
top of the model with and without TMD subjected to white noise
|
|

|
|
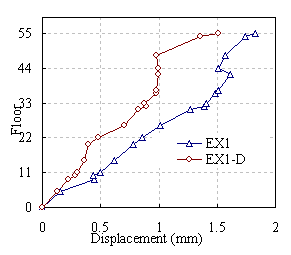
(a) PGA=0.14g
|
(b) PGA=0.4g
|
|
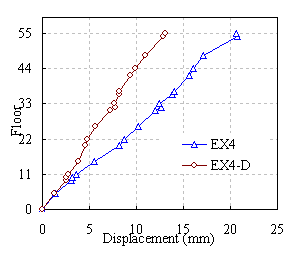
|
|
(c) PGA=0.88g
|
|
Figure 10 Displacement envelope in X direction under El-Centro ground
motion
|
|
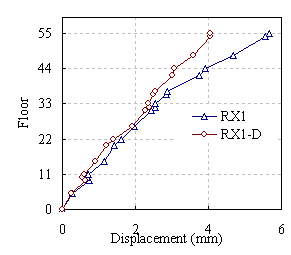
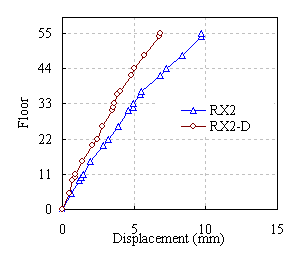
|
|
|
(a) PGA=0.14g
|
(b) PGA=0.28g
|
|
Figure 11 Displacement envelope in X direction under artificial accelerogram
|
|
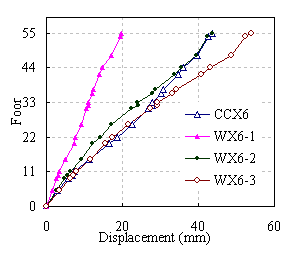
|
|
Figure 12 Displacement envelope in X direction under other ground
motions
|
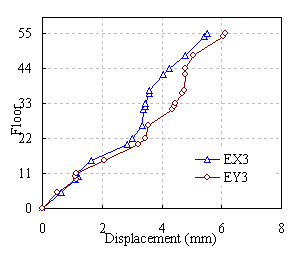
Figure 13 Displacement envelope in X direction of load case EX3 and EY3
|

|

|
|
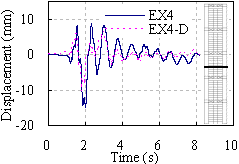
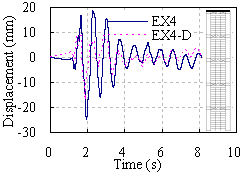
(a) Floor 26 (substructure)
|
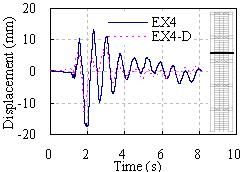
(b) Floor 36 (substructure)
|
|
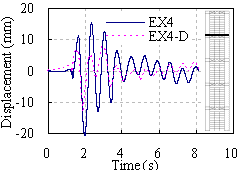

|

|
|
(c) Floor 44(mega-frame)
|
(d) Top floor(mega-frame)
|
|
Figure 14 Lateral displacement responses under El-Centro ground
motion of 0.88g
|
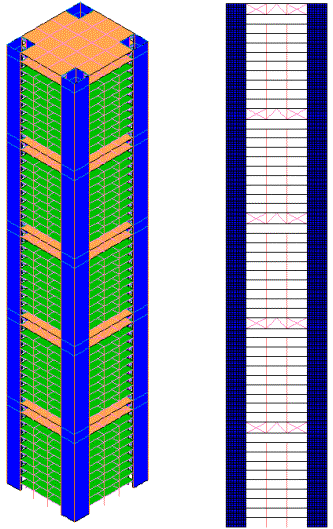

Figure
15 The FE model
|
|

|
|
(a) Without
TMD
|
(b) With
TMD
|
|
Figure
16 Displacement envelope under El Centro ground motion of 0.88g
|
|

|
|
Figure 17 Inter-story drifts under El Centro ground motion of 0.88g
|
|
![]() ,
, ![]() (3)
(3)