3 城市区域的地震灾变模拟
近年来,全球范围内地震频发,从2008年到2012年,全球上7级以上大地震共发生了111起[36],其中有两起大地震发生在我国内陆地区,分别是2008年的汶川地震和2010年的玉树地震。不仅如此,中、小型地震也频频发生。从2008年到2012年,我国共发生了5级以上地震206起[36],小震更是不计其数。城市人口密度和财产密度都非常高,尤其是特大型城市,一旦发生强烈地震,必然会造成严重的人员伤亡和财产损失。中小地震引起的非结构构件破坏和室内设备损坏,也可能导致非常严重的损失。因此,科学、合理地进行城市区域震害预测是目前我们国家乃至世界范围内的一项迫切需求。
3.1 城市区域建筑震害模拟的精细化建模
3.1.1 精细化建模需求
在过去的30年,基于易损性矩阵的区域建筑震害预测方法得到广泛应用[37],该方法通过给出不同场地烈度下某类型建筑达到不同破坏状态的概率(此概率一般可通过历史震害经验调查得到)来对震害损失进行预测。但是易损性矩阵方法只能给出宏观和统计意义上的预测结果,无法反映具体建筑物的详细损伤情况,也难以反映某一具体地震事件的特点。因此,基于能力-需求分析的建筑震害预测方法也得到了大量研究[38-40] 。例如,Hazus 99 的Advanced Engineering Building Modules (AEBM)[39]通过计算建筑弹塑性能力谱和地震需求谱的交点得到性能点,进而根据性能点来判断建筑物的损失情况。该方法相对易损性矩阵方法有了很大的进步,它能够计算出每栋建筑的位移和最大绝对加速需求,因此可以更加准确地对结构构件和非结构构件进行损失预测,也可以考虑不同地震动之间的差异。然而,该方法仍存在以下两方面的问题:(1) 将实际建筑物简化为单自由度体系,无法考虑高阶振型影响;(2) 采用基于静力推覆的能力-需求分析,无法考虑地震动的一些特性(例如地震动时域特性和速度脉冲)的影响[41]。
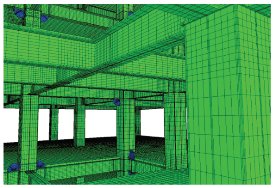
近年来,随着计算机数值模拟技术的不断发展,精细化模型和非线性时程分析越来越多地被应用于城市区域结构震害分析,但带来的问题是计算量过大。为了解决计算精度和计算效率之间的矛盾,本文作者[42]提出了采用GPU作为计算平台,以剪切层模型(如图3.1和图3.2)作为计算模型,采用非线性时程计算作为分析手段,进行高效城市区域震害分析的方法。剪切层模型有着比较适中的简化度以及相对较低的计算量[43],相对于单自由度体系,采用集中质量剪切模型可以得到结构每一层的破坏状态,结构高阶振型以及地震波的速度脉冲的影响也能够较好地考虑。国内外许多研究都证明了采用该模型进行多层建筑的地震响应模拟的可靠性[44-47]。然而,如何确定层模型中的层间滞回行为对保障预测结果的可靠性至关重要。对于城市区域,想要精确得到其中每座建筑每一层的侧移刚度和滞回参数是十分困难的,多数情况下仅能得到一些结构的宏观信息。国内外学者在此方面做了大量的研究[48-52],但是该问题尚未得到圆满解决。
本研究以Hazus软件作为基础,提出了相应的城市区域建筑物震害预测剪切层模型,并基于Hazus软件中通过大量调查统计得到的建筑抗震性能参数,提出了剪切层模型参数的确定方法,为精细化的城市区域建筑震害预测提供参考。
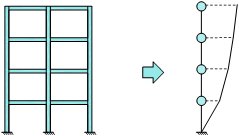
- 单体建筑集中质量剪切模型
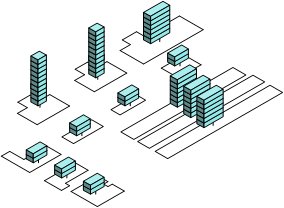
- 群体建筑集中质量剪切模型
3.1.2 结构类型和设防等级
Hazus将城市区域中一般建筑按照结构类型和高度分为36个建筑类型[53]。本研究考虑我国工程实际情况,选择了其中19种建筑类型(见表3.1)。对于同一建筑类型,Hazus考虑到不同建造年代设计规范的差异,其抗震性能参数也有所不同。本研究采用了Lin等[54]提出的Hazus抗震设计等级与我国建筑的对照关系(表3.2),用来确定我国建筑与Hazus所提供参数的对应关系。
- 本研究使用的建筑类型[53]
|
标签
|
描述
|
高度
|
|
包含范围
|
Hazus中
典型建筑
|
|
命名
|
层数
|
层数(N0)
|
高度 (m)
|
|
W1
|
木制框架
|
|
1 ‐ 2
|
1
|
4.27
|
|
S1L
|
钢框架
|
低层
|
1 ‐ 3
|
2
|
7.32
|
|
S1M
|
中层
|
4 ‐ 7
|
5
|
18.3
|
|
S1H
|
高层
|
8+
|
13
|
47.58
|
|
S3
|
轻钢框架
|
|
所有
|
1
|
4.575
|
|
C1L
|
钢筋混凝土框架
|
低层
|
1 ‐ 3
|
2
|
6.1
|
|
C1M
|
中层
|
4 ‐ 7
|
5
|
15.25
|
|
C1H
|
高层
|
8+
|
12
|
36.6
|
|
C2L
|
钢筋混凝土剪力墙
|
低层
|
1 ‐ 3
|
2
|
6.1
|
|
C2M
|
中层
|
4 ‐ 7
|
5
|
15.25
|
|
C2H
|
高层
|
8+
|
12
|
36.6
|
|
C3L
|
带砌体填充墙的钢筋混凝土框架
|
低层
|
1 ‐ 3
|
2
|
6.1
|
|
C3M
|
中层
|
4 ‐ 7
|
5
|
15.25
|
|
C3H
|
高层
|
8+
|
12
|
36.6
|
|
RM2L
|
带预制混凝土板的配筋砌体
|
低层
|
1 ‐ 3
|
2
|
6.1
|
|
RM2M
|
中层
|
4 ‐ 7
|
5
|
15.25
|
|
RM2H
|
高层
|
8+
|
12
|
36.6
|
|
URML
|
无筋砌体
|
低层
|
1 ‐ 2
|
1
|
4.575
|
|
URMM
|
中层
|
3+
|
3
|
10.675
|
- Hazus抗震设计等级与我国建筑对应关系[54]
|
设防烈度
(基本加速度)
|
建筑年代
|
|
1978年
以前
|
1979年至
1989年
|
1989年
之后
|
|
9度(0.40g)
|
Pre-Code
|
Moderate-Code
|
High-Code
|
|
8度(0.30g)
|
Pre-Code
|
Moderate-Code
|
Moderate-Code
|
|
8度(0.20g)
|
Pre-Code
|
Low-Code
|
Moderate-Code
|
|
7度(0.15g)
|
Pre-Code
|
Low-Code
|
Low-Code
|
|
7度(0.10g)
|
Pre-Code
|
Pre-Code
|
Low-Code
|
|
6度(0.05g)
|
Pre-Code
|
Pre-Code
|
Pre-Code
|
3.1.3 层间恢复力模型
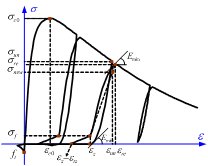
Hazus建议结构的骨架曲线可采用三线性模型(图3.3),本研究层间滞回模型的骨架线也采用此模型。该模型可以分别描述结构层间的弹性阶段,屈服阶段和塑性阶段。整个骨架曲线需要5个参数来标定:k0(初始侧向刚度),Vy (层间剪切屈服强度),η (强化系数),β (极限强度和屈服强度比)和 Δc (结构的层间极限位移)。
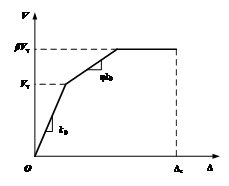
- 层间骨架线
不同结构在地震下往复受力行为有较大差异。根据结构类型的不同,本研究采用以下三种不同的层间滞回模型来描述不同类型的结构。
- 修正的Clough模型
修正的Clough模型[55](图3.4 a)被广泛应用于模拟弯曲破坏的钢筋混凝土框架结构,因此本研究采用该模型模拟钢筋混凝土框架结构的层间滞回关系(也就是C1类型)。
- 理想弹塑性模型
理想弹塑性模型(图3.4b)可以用于模拟钢框架结构。因此本研究采用该模型模拟钢框架结构的层间滞回关系(也就是S1和S3类型)。
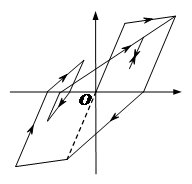
- 捏拢模型
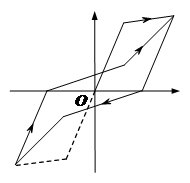
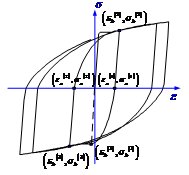
对于剪切破坏起主导作用的结构,采用捏拢模型(图3.4c)进行模拟是一个可行的方法。本研究采用Steelman和Hajjar[56]提出的捏拢模型。在该模型中,卸载刚度等于初始加载刚度,加载捏拢的转折点将出现在固定的转折线上,如图3.5所示。因此,本模型仅需1个描述结构退化程度的参数即可确定其滞回行为,如式\* MERGEFORMAT (3-1)所示:
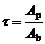 \* MERGEFORMAT (3-1) \* MERGEFORMAT (3-1)
其中 Ap和 Ab 分别是捏拢滞回包络面积和理想弹塑性滞回包络面积。选用该捏拢模型是因为其参数τ可以通过Hazus技术手册[53]提供的退化系数κ比较方便的确定[56]。如果采用其他多参数的捏拢模型(例如Ibarra捏拢模型[57]),参数标定的工作将非常复杂,不适用于区域震害预测的实现。在本研究中,除C1、S1、S3之外的所有建筑类型均采用此模型。
|
|

|
|
|
(a) 修正的Clough模型
|
(b) 理想弹塑性模型
|
(c) 捏拢模型
|
- 三种滞回模型
|

- 捏拢模型滞回行为
3.1.4 一般建筑剪切层模型参数确定
在Hazus中,在每一个抗震等级下,每一种结构类型都有一个典型建筑,可通过该典型建筑的已知的参数来标定该类型结构的抗震性能。这些参数包括:①结构初始弹性一阶周期;②结构性能曲线;③结构振型质量系数;④结构高度、楼层数;⑤结构材料弹性阻尼;⑥结构退化系数;⑦结构各个破坏状态所对应的层间位移角限值。
在本研究中,对于区域中的某一个目标建筑,仅需知道其结构类型、层高、层数、建筑年代、面积,就能通过Hazus已知的参数来确定其集中质量剪切模型的参数,具体方法如下:
(1) 结构周期
对于区域中的一般多层建筑,其地震响应主要受前两阶振型控制[58]。对于城市区域中的一般建筑,前两阶周期通过式\* MERGEFORMAT (3-2)进行计算[59]:
|
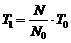
|
\* MERGEFORMAT (3-2)
|
|
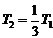
|
其中T1和T2分别是目标建筑的一阶和二阶振动周期,N是目标建筑的层数。N0和T0分别是Hazus给出的典型建筑的层数和一阶周期。
(2)结构骨架线参数
对于一般多层建筑,其层质量和层初始刚度可认为是各层基本相同的[39]。因此,剪切层模型的刚度矩阵和质量矩阵可写为:
 \* MERGEFORMAT (3-3) \* MERGEFORMAT (3-3)
 \* MERGEFORMAT (3-4) \* MERGEFORMAT (3-4)
其一阶圆频率可由式\* MERGEFORMAT (3-5)计算[58]
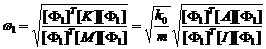 \* MERGEFORMAT (3-5) \* MERGEFORMAT (3-5)
其中[Φ1]是结构的一阶振型向量。如果结构的楼层数确定,则无论k0和m如何取值,[Φ1]的各自由度比例是确定的,且其值可以用广义特征值法很简便地加以确定[58]。
于是结构的层间初始刚度可由式\* MERGEFORMAT (3-6)计算
 \* MERGEFORMAT (3-6) \* MERGEFORMAT (3-6)
 \* MERGEFORMAT (3-7) \* MERGEFORMAT (3-7)
 取值与层数的关系见表3.3(为计算方便,表中给出的数值为的数值)。 取值与层数的关系见表3.3(为计算方便,表中给出的数值为的数值)。
- 取值与层数之间的关系(1至12层)
|
楼层数
|
|
楼层数
|
|
|
1
|
39.5 (4π2)
|
7
|
903.3
|
|
2
|
103.4
|
8
|
1159.3
|
|
3
|
199.3
|
9
|
1447.3
|
|
4
|
327.3
|
10
|
1767.3
|
|
5
|
487.3
|
11
|
2119.3
|
|
6
|
679.3
|
12
|
2503.3
|
于是,目标建筑第i层的层间骨架线参数(图3.3)可由式\* MERGEFORMAT (3-8)确定:
 \* MERGEFORMAT (3-8) (a) \* MERGEFORMAT (3-8) (a)
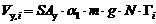 (3-8) (b) (3-8) (b)
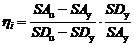 (3-8) (c) (3-8) (c)
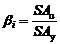 (3-8) (d) (3-8) (d)
其中m是结构每层的质量,可以根据结构层面积和建筑用途确定[60];g 是重力加速度;δCo是Hazus建议的结构完全破坏所对应的层间位移角限值[53];h 是结构层高;(SDy, SAy),(SDu , SAu) 是Hazus中给出的典型结构性能曲线的屈服点和极限点[53];α1是Hazus给出的典型建筑的振型质量系数[57];Γi是结构第i层的设计抗剪强度Vy,i与基底设计抗剪强度Vy,1的比值:
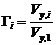 \* MERGEFORMAT (3-9) \* MERGEFORMAT (3-9)
在我国规范中,设计地震力随结构高度基本呈倒三角形[61]。在本研究中,Γi由式\* MERGEFORMAT (3-10)确定:
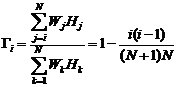 \* MERGEFORMAT (3-10) \* MERGEFORMAT (3-10)
其中Wj,Wk是结构第j,k层的重量,Hj, Hk则是结构第j,k层所在平面距离地面的高程。
(3)结构滞回模型参数
对于修正的Clough模型和理想弹塑性模型,其行为仅需要骨架线就可以确定。对于本研究给出的捏拢模型,则需要一个参数τ来确定其行为。参数τ的取值可以参照Steelman和Hajjar[56]提出的方法,取所对应结构类型在Hazus中的退化参数κm加以确定[53]。
(4)结构阻尼
本研究中,结构阻尼采用瑞雷阻尼进行计算[58],其阻尼比确定参照表3.4。
- 结构阻尼比取值[53]
|
结构类型
|
ζ=ζ1=ζ2
|
|
钢结构(S1,S3)
|
0.05
|
|
钢筋混凝土结构(C1,C2,C3)
|
0.07
|
|
砌体结构(RM2,URM)
|
0.10
|
|
木结构(W1)
|
0.10
|
(5)结构破坏状态限值
对于城市区域中一般建筑,其结构破坏状态采用Hazus定义的4种破坏状态:轻微破坏,中等破坏,严重破坏,完全破坏。而确定结构破坏状态的指标则采用位移角进行确定,其对应的取值可在Hazus手册[53]表5.9内查到。
3.1.5 特殊建筑剪切层模型的参数确定
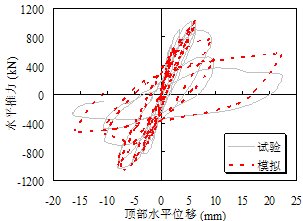
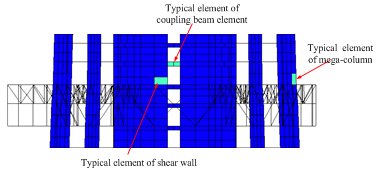
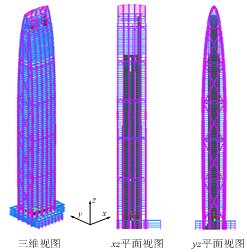
对于一些特殊建筑(如新型结构类型,混合结构,不规则结构),其抗震性能与一般多层建筑差别很大,Hazus软件对此类建筑也没有相应的规定。对于这类建筑,可采用更加精细的模型(如纤维梁模型或分层壳模型[11, 62-65])来确定其参数,如图3.6所示。
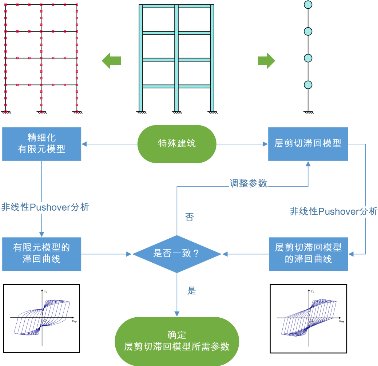
- 特殊建筑剪切层模型的参数确定流程
3.1.6 震害分析模型的数据获取
本研究中仅需获取结构类型、层高、层数、建筑年代、面积等5个参数,就能通过Hazus已知的参数来确定其建筑震害分析模型。然而,城市建筑数量庞大,每一栋建筑都需要采集相应的参数,这就导致城市区域建筑震害分析工作需要依赖详尽的城市基础数据库。当城市基础数据库的信息详尽程度难以满足震害分析需求时,如何高效、快速、准确地获取城市建筑的基础资料成为了一个重要问题。
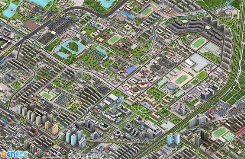
近年来Google Earth的城市区域3D建筑模型在全球各大城市依次上线,如图3.7。与此同时,国内的一些商业公司也逐渐完成了国内多个城市的区域3D数字模型,如图3.8。城市区域建筑的3D数字虚拟化正在成为一种趋势。城市区域3D建筑模型提供了精细的城市建筑尺寸信息。充分利用该数据,为城市区域建筑震害的模拟提供了一种新的数据获取思路。
为此,本研究提出了一种基于Google Earth城市区域3D建筑模型的建筑参数获取方法。该方法可以通过Google的Dae三维数字模型格式,获得分析区域内每一栋建筑的三维模型参数,如层高、楼面形状等,进而可以获得层高、层数、楼面面积等震害分析所需数据。
(1)方法介绍
在Google Earth城市区域3D建筑模型进行城市区域3D建筑几何参数的抓取,面临如下问题:
- 城市三维数字模型本质上是由多边形或者三角形组成的。Dae模型文件中仅包含所有多边形的端点坐标信息以及连接关系信息。事先通常不知道某栋建筑是由哪些多边形构成的,如图3.9所示。
- 城市三维数字模型中除了建筑模型,通常还包括地表,道路,植被等模型。因此需要剔除掉其他的模型,单独识别出构成建筑的多边形,如图3.9所示。
- 为了实现建筑的地震响应模拟,在获得到了组成某栋建筑的所有多边形之后,需要根据这些多边形数据,抽取出结构外形的参数。包括结构高度,结构各层的平面布置情况。
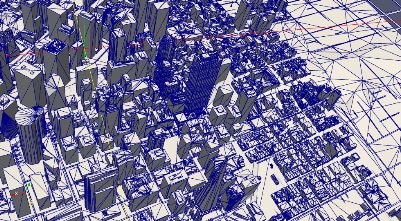
- 城市区域3D建筑模型示意
面对以上问题,本研究采用了基于城市切片的建筑参数抽取方法,具体实现步骤如下所示:
- 对整个城市区域3D模型中的所有多边形进行切片。对于每个多边形,得到对应该高程的一条直线。
- 提取出能围成闭合多边形的直线,将该多边形作为某栋建筑的层外形多边形,如图3.10所示。重复步骤2,得到各个高程的建筑层外形多边形,如图3.11所示。
- 判断各个多边形的竖向重叠关系,对于竖向重叠的多边形认为这些多边形组成一栋建筑,这样就获取到了区域中建筑的各层外形数据。
- 对于已经识别的建筑,计算其多边形的高程差,从而估算得到建筑的高度。

- 对模型的所有多边形进行切片
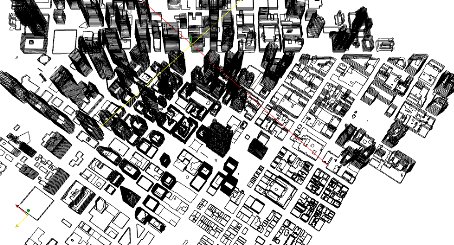
- 得到各个高程的建筑层外形多边形
(2)实例验证
通过上述的步骤,就能基本获得区域中建筑的各层外形参数以及各建筑的高度参数。为了校验本方法的可用性,首先可以对单栋建筑进行识别验证,如图3.12所示。图中半透明的模型为原建筑3D模型。橙色的部分为识别得到的各层建筑外形多边形。
此外对于整个区域,为了校验识别的效果,也可以与原模型进行对比,如图3.13所示。图中黄色部分为识别得到的建筑层外形多边形,可以看出虽然原模型中包含地形等无关的多边形数据。但是该方法依然能较好的识别出每一栋建筑。
通过识别出的建筑以及楼层多边形,可以快速计算楼层高度、楼层数量、楼层面积等建筑外形参数,为城市震害分析提供了重要的数据支持。

- 单栋建筑层外形多边形识别效果

- 区域建筑层外形多边形识别效果
3.2 城市区域震害模拟的高性能计算
3.2.1 基于GPU粗粒度并行的建筑震害计算
虽然基于精细化模型的非线性时程分析在单体建筑中已经得到了广泛的应用[66],但是城市区域拥有海量的建筑,该方法所需的计算量巨大。2008年Hori和Ichimura[67]基于精细化结构模型和非线性时程分析开发了Integrated Earthquake Simulation (IES) 平台,实现了整个东京的震害预测。但是该平台必须依赖超级计算机,这意味着高昂的运营费用和维护成本。因此,为了更好地开展城市区域建筑震害的精细化模拟,迫切需要一种低成本、高性能的计算平台。
最近几年,图形处理单元(GPU)技术飞速发展并在通用计算领域得到广泛应用。虽然GPU单核的计算能力相对CPU较弱,但是GPU的处理核心数远多于相同价格的CPU,因此相同价格的GPU相对CPU具有更高的计算性能[68]。随着NVIDIA公司发布了CUDA (Compute Unified Device Architecture ),GPU通用计算的编程难度被大大降低。目前GPU计算在生物、电磁场、地理等领域得到了大量的应用[69-71]。
最能发挥GPU性能的是细粒度的并行计算[72],即将每个子任务划分成许多更细小的操作步,然后GPU在操作步层面对任务进行并行计算。这种并行方式在神经网络以及有限元领域得到了很广泛的应用[73, 74]。但是这种并行计算方式需要对GPU程序进行细致的调试以实现对大量的操作步高效的运算,程序实现难度较大。而相对于细粒度的并行,粗粒度的并行方式则更容易实现。粗粒度的并行计算方式采用的是基于相对独立的子任务的并行而不是操作步的并行。这种并行方式在优化和控制领域都有应用[75]。当满足以下情况时,粗粒度和细粒度的并行效率相当:
(1) 子任务的数量远多于GPU计算的核心数;
(2) 每个子任务的计算量比较适中,能够独立在一个GPU核心上完成;
(3) 各个子任务之间不需要太多的数据交换。并且计算过程中不需要全局同步,每个GPU核心上的子任务可以按顺序逐个的进行计算。
幸运的是区域城市建筑震害预测分析可以满足以上三个特性。虽然整个城市有成千上万栋的建筑,但是如果通过采用适当的计算模型使每栋建筑结构的计算量不超过GPU单核的计算能力,则每栋单体建筑的计算就能被看作一个相对独立的计算子任务。此外不同建筑的地震响应相对独立,不同GPU线程之间几乎不需要进行数据交换。因此GPU数百计的计算核心可以实现几百栋建筑同时计算,这样计算效率将非常高。
本研究提出适合多自由度剪切层模型的GPU/CPU协同粗粒度并行计算的区域建筑震害预测方法,对并行计算的效率进行了详细的讨论,并对一个中等大小的城市进行了精细化的震害模拟。
3.2.2 CPU/GPU协同的程序构架
整个程序包括3个模块:前处理模块、结构分析模块和后处理模块。前处理模块的主要任务是获取计算模型的主要参数,并且选择地震场景进行非线性时程分析。后处理模块主要展示模拟结果并预测损失。
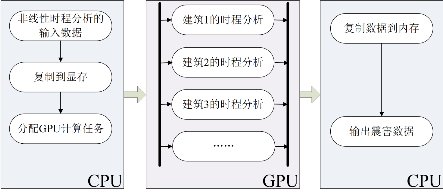
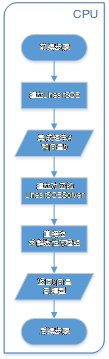
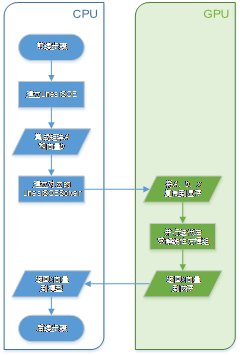
计算分析模块是程序的核心,由CPU和GPU协同完成计算任务。其中,CPU负责文件读写、任务分配等工作;GPU开启大量线程,每一条线程负责完成每一栋单体建筑的结构非线性时程计算,如图3.14所示。
本研究采用多自由度剪切层模型来模拟每个单体建筑物[42],它可以很好地平衡计算量和计算精度之间的关系。为了避免隐式动力计算的收敛性问题,并提高GPU并行计算效率,本研究采用中心差分法求解动力方程[58]。动力方程中的阻尼采用经典瑞利阻尼。
3.2.3 GPU计算性能分析
为了对比本研究提出的基于GPU/CPU协同粗粒度并行计算的结构分析模块的性能,在传统CPU平台上也开发了一个功能相同计算程序。本研究采用的对比算例和对比平台如下所示:
(1) 根据Hazus中的建筑类型,随机生成不同结构类型的1024栋建筑,如表3.5所示。
(2) 采用广泛使用的El Centro 地震动时程记录[76]进行对比分析。地震动时程记录的峰值加速按照200 cm/s2进行调幅。
(3) 计算时长为40s,时间步为8000步。
(4) 为了避免读写速度的影响,下文中的计算时间不包括硬盘的读写时间。
计算平台如表3.6所示。所采用的两套计算平台均为2011年采购,在当时两者价格基本相同。因此采用以上两套平台可以用于比较相同价格情况下的性能差异。
- 性能对比分析中使用的建筑结构类型分布情况
|
结构类型
|
类型描述
|
楼层范围
|
建筑数量
|
|
W1
|
木结构
|
1~2
|
51
|
|
S1L
|
低层钢框架结构
|
1~3
|
43
|
|
S1M
|
多层钢框架结构
|
4~7
|
55
|
|
S1H
|
高层钢框架结构
|
8~10
|
83
|
|
S3
|
轻钢结构
|
任意层数
|
54
|
|
C1M
|
低层RC框架结构
|
1 ~3
|
55
|
|
C1M
|
多层RC框架结构
|
4~7
|
58
|
|
C1H
|
高层RC框架结构
|
8~10
|
52
|
|
C2L
|
低层RC剪力墙结构
|
1~3
|
68
|
|
C2M
|
多层RC剪力墙结构
|
4~7
|
52
|
|
C2H
|
高层RC剪力墙结构
|
8~10
|
69
|
|
C3L
|
低层无砌体填充墙RC框架结构
|
1~3
|
51
|
|
C3M
|
多层无砌体填充墙RC框架结构
|
4~7
|
34
|
|
C3H
|
高层无砌体填充墙RC框架结构
|
8~10
|
49
|
|
RM2L
|
低层配筋砌体结构
|
1~3
|
51
|
|
RM2M
|
多层配筋砌体结构
|
4~7
|
57
|
|
RM2H
|
高层配筋砌体结构
|
8~10
|
47
|
|
URML
|
低层无配筋砌体结构
|
1~2
|
50
|
|
URMM
|
多层配筋砌体结构
|
3~7
|
45
|
|
总计
|
|
|
1024
|
- 对比采用的计算平台
|
平台
|
硬件部分
|
编译器
|
|
CPU
计算平台
|
Intel Core i3 530 @2.93GHz & DDR3 4G 1333MHz.
|
Microsoft Visual C++ 2008 SP1.
|
|
GPU/CPU
协同计算平台
|
Intel Celeron E3200 @ 2.4GHz & NVIDIA GeForce GTX 460 1GB.
|
Microsoft Visual C++ 2008 SP1 & CUDA 4.2
|
首先采用单栋建筑对比CPU平台和CPU/GPU协同计算平台的计算效率。楼层数和单栋建筑平均计算时间的关系如图3.15所示。从图中可以看出对于一栋建筑GPU/CPU协同计算的时间要长于CPU计算的时间,即单颗GPU核心的计算能力要明显弱于CPU的计算能力。此外还可以注意到对于一栋10层楼建筑,采用单精度计算GPU/CPU协同计算平台需要5秒,如果采用双精度计算则需要8秒。然而CPU平台的单精度和双精度计算时间非常接近(双精度还稍快),这是因为使用的CPU是基于64位构架,其默认计算精度就是双精度。
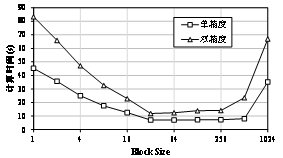
对于1024栋建筑物,如果改变CUDA的block size(每个计算块的线程数量),得到的计算时间如图3.16所示,可见当程序的block size为32时程序能达到最高的计算能力。这是因为,当采用CUDA进行并行计算的时候每32个线程组成一个wrap,而GPU计算任务的最小单位是一个wrap[77]。因此,如果block size小于32时,GPU的性能不能充分发挥。而当单精度的block size大于520或者双精度的block size 大于260时,将超出GPU中速度最快的寄存器的容量(本平台GPU每个block只能使用32K的32位寄存器,可存储32,768个单精度数或16,384个双精度数),因此也会导致并行效率下降。
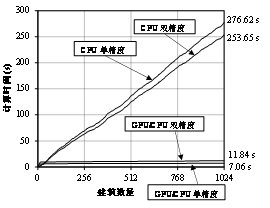
在1024栋建筑中,随机选取不同的建筑数量在CPU平台和GPU/CPU平台上进行性能对比(GPU/CPU平台的block size是32),结果如图3.17所示。CPU的计算时间与建筑的数量基本上是线性的关系。然而GPU/CPU协同计算平台的计算时间则主要取决于计算时间最长的那个线程(图3.17)。此外GPU/CPU协同计算平台双精度计算的曲线上有几个曲线的突跃,这是由于GTX460的双精度计算是在特殊函数单元中完成的 (Special Function Unit),其数量是CUDA核心数的1/6。这个问题可望在Fermi架构的Tesla GPU上得到修正,因为其双精度计算是直接在CUDA核心上完成的[77]。
由GPU/CPU平台与CPU平台的计算时间对比可以看出GPU对繁重的非线性时程计算具有巨大的速度优势。如图3.18所示,当对1024栋建筑进行单精度计算时,采用GPU/CPU协同计算的时间仅是CPU计算的1/39,如果采用双精度则是1/21。此外,本文作者[42]对比了GPU单精度和双精度计算结果,发现差异不足0.1%,因此对于区域建筑震害模拟而言,单精度计算已经可以满足要求。
3.2.4 中等城市的建筑震害模拟
以某中等城市为例应用本研究中提出的方法对该城市进行了建筑震害模拟,并讨论本研究方法的优势。该中等城市总共有4255栋建筑。将该地区的建筑按照表3.7对不同年代的建筑进行了抗震等级分类[54]。对不同的抗震设计等级将根据Hazus中提出的方法确定建筑结构的层间滞回参数[53]。不同结构类型建筑的统计信息如表3.8所示。
- 结构抗震标准的划分
|
|
建造时间
|
|
1978之前
|
1979-1989
|
1989之后
|
|
抗震标准
|
Pre-Code
|
Low-Code
|
Moderate-Code
|
- 该区域建筑的统计情况
|
结构类型
|
楼层范围
|
Moderate-Code
|
Low-Code
|
汇总
|
|
C1L
|
1~3
|
6
|
0
|
6
|
|
C1M
|
4~7
|
2421
|
428
|
2849
|
|
C2H
|
8+
|
14
|
2
|
16
|
|
RM2H
|
8+
|
5
|
1
|
6
|
|
S1H
|
1~3
|
4
|
0
|
4
|
|
S1M
|
4~7
|
6
|
21
|
27
|
|
URML
|
1~2
|
0
|
1
|
1
|
|
URMM
|
3+
|
0
|
1308
|
1308
|
|
W1
|
1~2
|
34
|
4
|
38
|
|
总计
|
|
2490
|
1765
|
4255
|
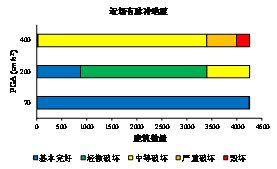
分析采用了3类地震动数据:远场地震动,近场无速度脉冲地震动,近场有速度脉冲地震动。对于每一类地震动,从FEMA p695推荐的地震动数据库中分别选取5条(表3.9)[78]。根据该城市的设防烈度,对于小震、中震、大震分别采用70, 200和 400 cm/s2的地面峰值加速度对选取的地震动记录进行调幅。由于本研究主要讨论建筑震害模拟方法,因此没有考虑场地对地震动的影响,每栋建筑都采用相同的地震动记录。
- 从 PEER-NGA 数据库中选择的地震动时程记录
|
编号
|
远场地震动记录
|
近场有脉冲
地震动记录
|
近场无脉冲
地震动记录
|
|
1
|
NORTHR/MUL009
|
IMPVALL/H-E06_233
|
GAZLI/GAZ_177
|
|
2
|
DUZCE/BOL000
|
ITALY/A-STU_223
|
IMPVALL/H-BCR_233
|
|
3
|
HECTOR/HEC000
|
SUPERST/B-PTS_037
|
NAHANNI/S1_070
|
|
4
|
IMPVALL/H-DLT262
|
LOMAP/STG_038
|
LOMAP/BRN_038
|
|
5
|
KOBE/NIS000
|
ERZIKAN/ERZ_032
|
CAPEMEND/CPM_260
|
为了体现本研究采用的多自由度剪切层模型的优势,将分别使用本研究的多自由度模型方法和传统的单自由度模型方法对该城市进行模拟,单自由度模型的参数根据Steelman和Hajjor建议的方法[56]确定。对于这样一个中等城市,多自由度剪切层模型和单自由度模型完成一次地震模拟的计算时间完全可以满足应急震害预测的速度要求。
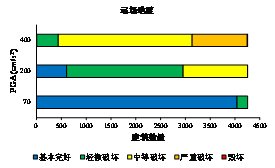
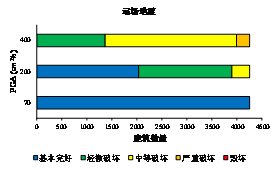
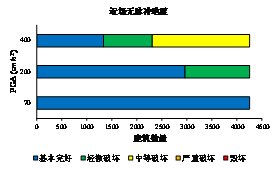
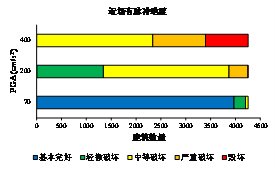
计算得到的最大楼层损伤状态的分析结果如图3.19所示。图中结果显示采用多自由度剪切层模型得到的楼层损伤结果普遍比单自由度模型的预测结果大一些。这是由于多自由度剪切层模型可以得到各个楼层的响应,从而能够考虑损伤集中现象。对于200gal远场地震波记录和近场无速度脉冲地震动记录,单自由度模型和多自由度剪切层模型的结果差异较小。但是对于近场有脉冲地震动记录,单自由度模型和多自由度剪切层模型的结果具有较大的差别。这是由于速度脉冲能够激励出高阶阵型从而导致结构更加严重的破坏,而单自由度模型无法考虑高阶阵型的影响。
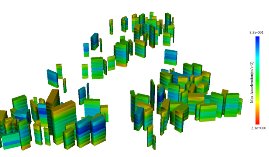
以峰值加速度为200 cm/s2 的IMPVALL/H- BCR_233地震动为例,建筑破坏的预测结果如图3.20、图3.21所示。结果显示采用多自由度剪切层模型,能够准确获得建筑损伤的楼层位置和最大加速度位置,显著优于单自由度模型的计算结果。
本研究的结果可以证明GPU/CPU协同粗粒度并行计算具有很高的计算效率,其性能价格比能够达到传统CPU计算的39倍。并且,采用的多自由度剪切层模型可以考虑地震动中速度脉冲的影响,也能确定不同楼层的损伤情况,从而能够更加准确的进行损失预测。
3.3 城市区域震害的高真实度展示
3.3.1 震害真实感展示的需求
城市区域震害模拟的高真实度展示对防灾规划、虚拟应急训练、成果交流等都具有重要意义。在这方面,国内外很多研究者已经开展了基于三维城市模型的震害展示研究,如加拿大约克大学[79]基于分布式GIS建立了温哥华的三维地形和城市模型,并对城市整体震害进行评估;土耳其中东技术大学[80]、清华大学[81]利用CAD和纹理技术建立了真实感的3D城市,通过静态方式展现地震易损性或震害效果。但是这些研究所采用的震害预测模型往往过于简单,不能得到建筑物破坏的细节信息,因而其震害展示效果真实感不够。而近年来得到迅速发展的城市建筑群精细预测模型[60, 67],可以得到更加清晰准确的震害计算结果(例如整个结构的震害时程以及楼层的局部损伤等),为提高震害模拟的真实感提供了关键的数据支持。
但是,精细化的区域建筑震害预测模型一般也难以包含建筑倒塌过程、残骸运动等倒塌细节。缺乏倒塌细节不仅影响震害模拟的真实感,也无法评价建筑倒塌对交通、救援等的影响。物理引擎[82]是近些年计算机图形学的新技术,专门用于计算场景中物体的复杂物理行为,可以模拟震害场景中建筑物的开裂、破碎、碰撞、堆积等一系列破坏过程,在科学仿真、电影制作上有相关应用[83-85]。应用物理引擎技术,可以弥补数值模拟缺失的细节,如清华大学[86]曾用物理引擎技术模拟桥梁垮塌全过程中残骸的运动,弥补有限元“生死单元”技术的不足。因此,物理引擎技术也可以应用在城市震害模拟中,为城市工程震害的动态破坏细节过程提供了技术支持。然而,国内外尚缺乏基于物理引擎等技术的城市工程震害视景仿真方面的深入研究,因此,在震灾真实感展示中,垮塌过程的真实感特效问题面临较大挑战。
本研究基于城市区域建筑震害精细化数值分析结果,提出真实感的城市区域建筑三维建模方法以及震害过程的动画实现方法,以准确而又真实感的表现震害分析结果;利用物理引擎,提出建筑震害过程中的垮塌效果的实现算法,以弥补数值模拟缺乏的细节,增加模拟完整性和真实感。并且,对我国一个中等规模城市的建筑震害过程进行综合模拟,为城市防灾减灾策略提供参考意见。
3.3.2 真实感建模与震害动态演示
(1)城市建筑群的真实感建模
城市建筑群的真实感建模主要包括三维建模和纹理映射两个部分,如图3.22所示。区域建筑震害预测模型将楼层简化为集中质量点,并不包含完整的三维信息。因此,需要利用城市区域的地理信息系统GIS数据,获取位置、建筑外形、楼层高度等扩充信息来建立建筑三维模型。本研究采用徐峰等人的基于GIS三维城市建筑建模方法[81],利用GIS中建筑轮廓多边形在高度方向进行拉伸来建立不同的建筑三维模型。同时,为了使建筑三维模型能够反映层间的局部震害特征,建筑三维模型应与震害预测模型保持一致,同样以楼层为基本单元。
为增加建筑模型的真实感,需要对三维模型进行纹理映射。本研究基于Tsai和Lin的方法[87],采用多重纹理技术,对建筑物的不同表面分别进行贴图,以更加细致地体现建筑物的特征。根据图3.22所示方法,可以建立城市区域的真实感模型,为震害动态演示奠定基础。
(2)基于精细化预测的震害动态演示
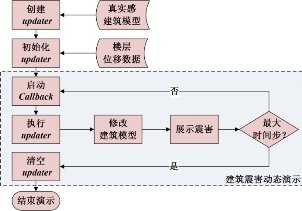
如何准确、高效地表现大规模的震害预测的时变数据是本研究城市区域建筑震害动态演示的主要问题。为了对图形表现过程进行充分控制,本研究选择开源图形引擎OSG(Open Scene Graph)作为视景模拟的主要平台[88]。在OSG中,一般会采用回调机制(Callback)来完成每一帧渲染前需要的工作,如空间变化、顶点更新、视点变化等。利用OSG的回调机制,本研究直接用震害预测数据在每一帧更新建筑模型的顶点坐标,以动态地表现建筑震害过程,具体算法如图3.23所示。
图3.23所示算法包含三个重要步骤:
1)更新器的创建与初始化
为了实现对图形顶点的操作,需要创建更新器updater。它需要继承OSG中图形的更新回调类UpdateCallback,以实现对回调过程的全面控制。在updater初始化阶段,更新器需要在动画渲染前加载对应建筑震害的节点位移数据。
2)更新器的动态执行
在回调过程中,需要将震害预测中的时间步与动态演示中的帧数相对应。在动态演示的每一帧中,更新器将利用对应时间步的震害数据来更新建筑的顶点坐标。重载更新器中的Update()函数可以实现对图形顶点的动态修改功能。通过回调,不断修改建筑模型,可形成区域建筑震害的动态演示过程。
3)清空更新器
当动态演示达到最大的时间步时,清空更新器,建筑模型不再更新,震害过程的动态演示结束。
3.3.3 基于物理引擎的倒塌模拟
区域震害预测模型只能给出建筑倒塌的判断,缺乏细节的倒塌过程。细节的倒塌过程可以增强震害模拟的真实感,也为地震疏散、救援调度等提供重要的参考,因此,倒塌模拟在地震模拟中是不可缺少的。而且,倒塌过程需要符合物理规律,并不是纯粹的图形表现。
为匹配上述需求,本研究选择物理引擎模拟建筑倒塌过程。由于在多刚体动力学和碰撞检测上的优势,物理引擎善于模拟倒塌过程中大量残骸的复杂运动和相互碰撞过程。本研究对比了三大物理引擎Havok,PhysX和Bullet[89-91],发现由于PhysX可以采用GPU来加速计算过程,更适合大量物体的计算,而在区域震害模拟中,建筑的规模是庞大的,因此,PhysX更适合用于区域建筑的倒塌过程模拟。
为了保证物理计算与图形显示的准确对应,需要根据震害预测数据在物理空间中建立与图形一致的建筑倒塌模型。在本研究建筑模型场景层次中,楼层图形由OSG中的Geode节点储存和管理[88]。在PhysX中,物理角色Actor类是基本的计算单元,代表着物理世界中所有的物体[91]。因此,对应于Geode节点,在物理引擎中楼层由Actor建立。物理引擎的楼层模型,需要楼层的材料属性(如弹性系数、线阻尼等),也需要楼层倒塌时的状态参数(如位移、速度等)。材料属性需要根据不同建筑结构类型,查询相关实验结果确定,而状态参数通过数值分析数据获得,以保证模拟的准确性。在物理引擎中,楼层的外形参数通过对应的楼层的Geode节点获得。为减少震害模拟过程中的耗时,楼层的物理模型可以在渲染前建立,在需要物理计算时被激活。
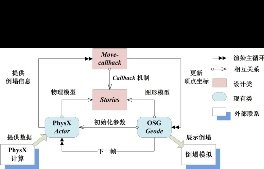
物理引擎与图形引擎是两个独立的程序,需要构建两者的动态联系才能模拟建筑的倒塌过程。目前,关于OSG与PhysX的结合工作研究还非常有限。本研究中基于OSG回调机制,在每一帧中,利用PhysX实时计算数据不断更新楼层的顶点坐标,以形成楼层倒塌过程的动态演示[88]。为了建立OSG与PhysX的对应关系,创建了一个专门的类Stories。在Stories类中,同时包含楼层对应的Actor对象和Geode节点,以建立楼层物理模型与图形模型的联系。为了实现建筑倒塌的动态过程,需要控制Stories类的回调过程,因此,设计了一个新类Move-callback。由于继承了Callback机制的控制类,Move-callback类可以控制Stories类的渲染主循环。Move-callback类从PhysX的Actor中获取运动信息,然后应用运动信息来更新楼层图形。通过Stories类和Move-callback类实现的渲染循环过程形成了PhysX计算支持的建筑倒塌模拟,如图3.24所示。
建立OSG与PhysX的动态联系后,可以通过物理引擎模拟建筑倒塌过程。但是,为表现完整的建筑震害过程,震害动态演示与倒塌过程必须形成协同模拟的整体。根据震害预测给出的倒塌判断,将整个建筑震害过程分为两个阶段:倒塌前和倒塌后。首先,建立区域建筑群的真实感模型。在倒塌前,利用位移时程数据来动态地演示建筑的位移和变形。发生垮塌后,清空动态演示的更新器,根据前述方法建立楼层图形Geode节点与物理角色Actor的动态联系。然后,将Geode的运动状态信息传递给Actor,并激活Actor。物理引擎将不断计算Actor的倒塌过程,计算数据也会同步传递给Geode,以实时地楼表现建筑的倒塌过程。上述过程(如图3.25所示)实现了完整的城市区域建筑震害高真实度模拟。
3.3.4 中等城市的震害真实感展示
本研究以前文中的中型城市震害模拟作为算例,基于精细化震害预测结果和GIS数据建立了真实感的三维城市模型(图3.26a),并展示了震害过程中不同楼层间的位移和变形(图3.26b)。由于城市区域的建筑数量众多,所有建筑倒塌过程的非线性时程分析是不可能通过普通计算机模拟的。然而,通过使用PhysX,可以在桌面型计算机中快速模拟建筑倒塌过程(图3.26c 和 图3.26d)。倒塌过程模拟很好地弥补了非线性时程分析的不足,使整个震害模拟过程更加真实、完整。
为进一步增加震害场景的完整性和真实感,本研究将震害场景加入了地形、天空等环境模型,并且利用立体投影设备进行了区域建筑震害过程的立体感展示,进一步加强了震害过程模拟的沉浸感,如图3.27所示。图3.27的结果可以用于虚拟环境下地震疏散、应急调度等应用,综合提升防震减灾能力。
本研究基于精细化的结构模型和物理引擎技术,实现了城市区域建筑震害的真实感显示,对我国一个中型城市进行了区域建筑震害模拟。本研究不仅准确、真实感地表现了区域建筑震害过程,同时,也给出符合物理规律的倒塌过程,弥补了震害模拟的细节缺失。研究结果可以用于震害预测、灾后应急、救援训练等,为城市防震减灾提供了重要技术支持。
|




 \* MERGEFORMAT (2-1)
\* MERGEFORMAT (2-1)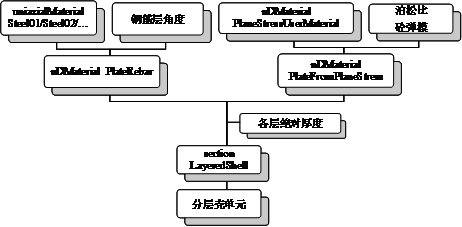











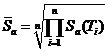 \* MERGEFORMAT (2-2)
\* MERGEFORMAT (2-2)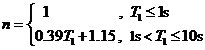 \* MERGEFORMAT (2-3)
\* MERGEFORMAT (2-3)








 \* MERGEFORMAT (3-3)
\* MERGEFORMAT (3-3) \* MERGEFORMAT (3-4)
\* MERGEFORMAT (3-4) \* MERGEFORMAT (3-6)
\* MERGEFORMAT (3-6)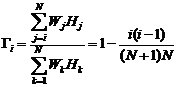 \* MERGEFORMAT (3-10)
\* MERGEFORMAT (3-10)