1 Introduction

Structures may be subjected to various hazards during their service live including earthquakes, windstorms, fires, and progressive collapse due to accidental local damage. Therefore, the structural design against multi-hazards is emerging. Many studies suggest that earthquakes and progressive collapse are the main hazards influencing the structural safety of steel-concrete composite frame buildings [1-5]. Presently, steel-concrete composite frames have relatively mature seismic and progressive collapse design procedures [6-9]. In brief, design against progressive collapse ensures that the remaining structure has sufficient internal force redistribution capacity after the localized damage due to accidental loading. On the other hand, seismic design is primarily concerned with lateral loading. Prior studies have shown that the design methods for specific hazards influence the structural performance against other hazards [10-12]. For example, Lin et al. [13] showed that the beam strength within a frame may significantly increase due to progressive collapse design considerations, thereby violating the capacity design principles such as the strong-column/weak-beam ratio, which is relevant for seismic-resistant design. Therefore, alternative solutions are necessary to meet both design requirements in order to ensure the structural safety. At the same time, new design concepts and structural system typologies should promote the minimization of structural damage and residual deformations in an effort to enhance seismic resilience.

To date, many innovative concepts have been proposed to comply with the aforementioned principles. In particular, systems that exhibit self-centering characteristics with replaceable energy-dissipating components show promise in minimizing residual deformations after an earthquake [14-16]. Along these lines, post-tensioned steel moment resisting frames with semi-rigid connections were developed to control the seismic demands [14, 17, 18]. Wang et al. [19, 20] used shape memory alloy rods or the combination of shape memory alloy rods and angle steels in beam-to-column connections to achieve seismic resilience. Flange friction devices [15, 21] and web friction devices [22, 23] were used in self-centering steel moment resisting frames to dissipate the seismic energy. Eatherton et al. [24] developed a self-centering rocking steel-braced frame with replaceable steel energy dissipating fuses to minimize residual deformations after seismic event series. The primary focus of the aforementioned studies was mostly on how to minimize the seismic effects on the structural behavior of self-centering systems. On the other hand, only a handful of studies focused on the progressive collapse performance of self-centering systems. For example, Vasdavellis et al. [25] studied the robustness of seismically designed self-centering moment resisting frames in a progressive collapse scenario. The results showed that the frame is able to provide catenary action and withstands large rotations in the beam-column connections. But the hourglass shape stainless steel energy dissipation devices adopted for beam-column connections cannot be replaced, which affects the self-centering performance of structures. Finite element modeling and capacity analysis of post-tensioned steel frames against progressive collapse were developed by Pirmoz and Liu [26]. The results showed that the resistance of energy dissipating elements is one of the major sources of structural capacity against progressive collapse. The disadvantage of this type of semi-rigid connection is that it exhibits lower stiffness and strength compared to traditional bolt-welded connections or full-welded connections. Additionally, limited work has been reported on both seismic and progressive collapse resistant structures, as well as the corresponding experiments. In addition to the study of the beam-to-column connections, some researchers have recently investigated various types of concrete columns with the consideration of resilience [27-31] or multi-hazard defense [32]. For example, Rousakis [28] studied the inherent seismic resilience of reinforced concrete columns externally confined with nonbonded composite ropes, and the results showed that their proposed columns exhibited an excellent energy-dissipating performance. Echevarria et al. [32] summarized the findings of blast, fire, and seismic experiments performed on the concrete-filled fiber reinforced polymer tube (CFFT) specimens, and developed a set of experimentally validated design equations, which is expected to promote the application of lightly reinforced CFFT columns to enhance the multi-hazard resilience. The abovementioned columns can be incorporated into the proposed seismic and progressive collapse resistant composite frame in potential future applications.

The present paper presents a design concept against seismic action and localized damage due to accidental load that could lead to progressive collapse. The design concept comprises a seismic and progressive collapse resistant composite frame (SPCRCF). This frame exhibits self-centering characteristics by utilizing pre-stressed steel strands and replaceable energy-dissipating components in its connections. The SPCRCF¡¯s resistance against earthquakes and progressive collapse is experimentally validated and directly compared with that of conventionally designed frames. Subsequently, the general-purpose finite element software, MSC.Marc [33], was used to simulate the behaviors of the specimens. The outcomes can facilitate the further researches on the multi-hazard design of structures.

2. Proposed seismic and progressive collapse resistant composite frame

Figure 1a illustrates the proposed SPCRCF. The beam-column connection of the SPCRCF is shown in Figure 1b. The SPCRCF comprises concrete-filled steel tube (CFST) columns, H-shaped steel beams, pre-stressed steel strands, replaceable energy-dissipating components, and shear panels. The pre-stressed steel strands provide self-centering capabilities, thereby minimizing the likelihood of residual deformations. The replaceable energy-dissipating components involve angle steels and rib stiffeners (see Figure 1c) that dissipate energy through yielding during a seismic event [34]. In order to balance the energy dissipation and self-centering performance of the connection, the yield moments provided by the energy-dissipating component and the pre-stressed steel strand are designed to be 50% of the respective yield moment of the web-bolted and flange-welded connection or welded connection. Referring to Figure 1d, a shear panel is utilized to realize the final beam-to-column connection assembly. The general goal is to mainly concentrate the earthquake-induced structural damage in the replaceable energy-dissipating components without damaging the CFST columns and steel beams.

Figure 1a shows the deformed configuration of an SPCRCF subjected to a column-removal scenario. The shear panels are designed to accommodate large rotational demands under a column removal scenario. By utilizing the replaceable energy-dissipating components together with the pre-stressed steel strands, sufficient progressive collapse resistance is provided through alternate load distribution paths once a column is lost due to accidental damage.

3 Experimental program

3.1 Prototype composite frame building

To ensure that the specimens in this work agree with the actual situation in real buildings, a real tall building (denoted as Building L) was selected as the prototype structure [35]. As such, the realized connections are deemed to be rational. In brief, Building L is a 51-story frame-core tube structure with a total height of 211.75 m. The seismic design intensity of the building is 7-degree, whose peak ground acceleration (PGA) corresponding to the exceeding probability of 10% in 50 years is 100 cm/s² [36]. The seismic performance of Building L follows the requirements of the Chinese Code for Seismic Design of Buildings (GB50011-2010) [36]. Note that there are significant differences between the Chinese and the US standards in the specification of story drift ratio limits [37]. The story drift ratio requirement given in the Chinese code is more rigorous. According to the requirements of GB50011-2010 [36], the inelastic story drift ratio limit of Building L is 0.01 rad under the maximum considered earthquake (MCE), which is smaller than that specified by ASCE/SEI 7-16 (i.e., 0.02 rad) [38].

The main lateral resisting system of Building L includes the peripheral composite frame and a reinforced concrete core tube. The peripheral composite frame of Building L, comprised of CFST columns and H-shaped steel beams, is the main research focus of this work. The CFST columns were fabricated by Q345 steel with a nominal yield strength f_y = 345 MPa and C50 concrete with a compressive strength of 50 MPa. H-shaped steel beams utilized Q345 steel with a nominal yield strength f_y = 345 MPa. Table 1 summarizes the primary geometric properties of the structural components of the peripheral composite frame.

Table 1 Dimensions of the structural components of Building L

3.2 Description of test specimens and testing apparatus

Due to the testing facility¡¯s loading and space capabilities and equipment limitations, the test specimens were scaled to 1:2.4. The final cross-sections and overall geometric properties of the test specimens are summarized in Table 1. These were fine-tuned compared to the original scale such that practical cross-sections could be purchased and the CFST columns would still remain elastic as intended. In total, four specimens were tested. Two of them (named as B-S and M-P100-S) were subjected to a symmetric cyclic loading protocol to mimic a seismic event. The test apparatus in this case is shown in Figure 2. It represents a typical cruciform beam-to-column subassembly. The rest of the specimens (named as B-C and M-P100-C) were subjected to a load protocol representing progressive collapse due to a column removal scenario. The test apparatus in this case is shown in Figure 3 and it involved two bays to properly characterize the catenary action of the beam.

Referring to Figure 2, during the cyclic tests, a constant axial compressive load of 1160 kN was directly applied at the column top end to simulate the gravity-induced compressive load from the upper stories. The beams were subjected to cyclic loading that involved two loading cycles per drift amplitude. The load was imposed through displacement control. The beam-to-column rotation angle, q was obtained by measuring the displacement of the loading point at the beam end (denoted by D), i.e., q = D / L. To put the test results into perspective, AISC 341-16 [38] requires that at least 80% of the beam¡¯s flexural strength shall be maintained for composite special moment frames at q  = 0.04 rad.

Referring to Figure 3, the end columns of Specimens B-C and M-P100-C were mounted to the strong frame to represent an ideally fixed boundary condition. To simulate a middle column-removal scenario, a downward load was imposed monotonically at the interior column¡¯s top end under displacement control. Lateral restraint devices were installed to prevent torsion and out-of-plane displacement of the interior column stub end as well as the steel beams.

Figures 4a and 4b show the detailed drawings for Specimens B-S and M-P100-S, respectively.

Similarly, the detailed drawings of Specimens B-C and M-P100-C are shown in Figures 5a and 5b, respectively. As indicated in Figures 4 and 5, the structural details of the beam-to-column connections are identical between the various specimens including the basic dimensions of the respective members comprising the connection itself. Geometric information of the angle steels and rib stiffeners in Specimen M-P100-S(C) is shown in Figures 6a and 6b. Lu et al. [34] proposed the design and fabrication methods for the energy-dissipating components comprised of the abovementioned angle steels and rib stiffeners. The dimensions of the shear panels in Specimen M-P100-S(C) are shown in Figure 6c. The sectional size of the shear panels meets the shear strength requirements given in the Standards for Classification of Steel Structures (GB 50017-2017) [40]. The design principle for the center-to-center length d_s of the slotted hole shown in Figure 6c is to ensure that the rotation of the beams can reach 0.2 rad (i.e., the required chord rotation in DoD [41]) under a middle column-removal scenario. Each pre-stressed steel strand in Specimen M-P100-S(C) is 15.2-7F2.5 (i.e., a strand with a nominal diameter of 15.2 mm is comprised of 7 steel wires with 2.5 mm diameter). The configuration of the strands in Specimen M-P100-S (C) is shown in Figure 6d. Each steel strand was initially pre-stressed to 100 kN. This corresponded to an approximately 40% of the initial pre-stressed level, which was determined by the condition of the maximum residual bending moment of the replaceable energy-dissipating components when q  ¡Ü 0.04 rad. Design of the pre-stressed steel strands followed the method proposed by Zhang et al. [42]. The yield moment provided by the pre-stressed steel strand was designed to be 50% of the yield moment of Specimen B-S(C). Through the subsequent finite element analysis, the compressive strain distribution along the central axis of the beam after prestressing can be obtained, which is shown in Figure 7. The average compressive strain is 461 me, whose error is less than 5% compared with the theoretical value. A set of 10.9 grade M24 friction high-strength bolts was used between the energy-dissipating component and the beam (column). The nominal diameter of each bolt is 24 mm, and its nominal peak and yield strengths are 1000 MPa and 900 MPa, respectively. The preload of each bolt is 225 kN, which satisfied the requirement of GB 50017-2017 [40]. When the column is very wide, bolt nuts can be embedded in the column. It can be found from the results of Specimen M-P100-C that the nuts still remained intact when the bolts were broken. Therefore, such a design and detailing method will not affect the resilience of a structure. Meanwhile, the inner diaphragm can be used to strengthen the column to avoid local buckling of the outer layer of the composite column due to tension developed in the bolt.

Figure 6 Dimensions of components in Specimen M-P100-S(C) (unit: mm)

Figure 7 Compressive strain distribution along the central axis of the beam after prestressing

3.3 Material properties

Table 2 summarizes the measured material properties. These properties are based on three standard tensile coupon tests [43]. The 28-day concrete compressive strength was f_{cu, m} = 61.05 MPa based on a standard cubic (150 ¡Á 150 ¡Á 150 mm) compressive test. According to the material test, the ultimate yield strength and the maximum tensile force of each pre-stressed steel strand are 1933 MPa and 270.8 kN, respectively. Referring to the recommendation of the Technical Specification for Concrete Structures Prestressed with Unbonded Tendons (JGJ 92-2016) [44], the elastic modulus of the pre-stressed steel strand is E = 1.95¡Á10⁵ N/mm². Referring to ACI 550.3-13 [45], the pre-stressed steel strand model proposed by Mattock [46] is adopted in this work. According to Mattock [46], the stress-strain relationship of the pre-stressed steel strand can be expressed by Equation 1:

where E is the elastic modulus of the pre-stressed steel strand; f_py is the yield strength of the strand, which can be approximated as 90% of the ultimate strength; e is the strain of the strand, which can be calculated by e = e₀ + De ; e₀ is the initial strain.

Table 2 Material properties of the various steel components

Thereafter, the stress-strain curve of the pre-stressed steel strand determined by Equation 1 can be expressed in Figure 8.

Figure 8 ¦Ò-¦Å curve of the pre-stressed steel strand

4 Test results and Observations

4.1 Specimens subjected to cyclic loading

The load-rotation relationships of Specimens B-S and M-P100-S are shown in Figure 9 with key reference points associated with the specimen¡¯s hysteretic behavior that are linked to Figures 10 and 11. Referring to Figure 9, Specimen B-S, which is a typical conventional composite moment-resisting frame (MRF) construction, exhibited local buckling at the lower flange of the south beam at ¦È = 0.019 rad. Figure 10a illustrates the local buckling initiation at this rotation. Notably, web local buckling occurred in the north beam at q = 0.044 rad (see Figure 10d). Finally, at q = 0.055 rad (the corresponding beam end displacement was 76.8 mm), the lower flange of the south beam ruptured (see Figures 10e and 10f), thereby ending the loading process due to safety considerations. Due to uncertainties associated with the material processing, specimen assembly and installation as well as the imposed loading, the hysteretic behavior of the specimens were not fully symmetric.

Figure 10 Damage progression of Specimen B-S

Referring to Figure 9, Specimen M-P100-S dissipated appreciable hysteretic energy through the rib stiffeners¡¯ inelastic deformation (see Figure 11a); at q = 0.040 rad (the corresponding beam end displacement was 56 mm), the rib stiffener under the north beam ruptured (see Figure 11b). Because q has already exceeded 0.04 rad (i.e., the deformation criterion in AISC 341-16 [39]), the loading process ended.

Figure 12 suggests that the initial stiffness and strength of Specimen M-P100-S were similar to those of Specimen B-S. FEMA P-58 [47] specifies that a structure can be repairable when the residual story drift ratio is less than 0.5% rad. From the results summarized in Figure 9 based on a standard symmetric loading history, Specimen B-S is not repairable if q exceeds 0.019 rad. In contrast, Specimen M-P100-S is repairable until q exceeds 0.028 rad. Thus, the deformation capacity of SPCRCF is increased by 47.4% compared with that of the conventional frame when satisfying the resilience requirement. Note that a drift ratio of q = 0.028 rad is already larger than the allowable story drift specified in Table 12.12-1 of ASCE/SEI 7-16 [38]. Furthermore, the key components (beams and columns) of the SPCRCF joint were damage-free up to 0.04 rad. Consequently, SPCRCF has significantly higher resilience than the conventional frame.

Furthermore, the members (beams and column) of Specimen M-P100-S did not exhibit any noticeable structural damage. Figure 13 shows the engineering strain of the angle steel (see Figure 13a) and shear panel (see Figure 13b) as well as the internal force of the pre-stressed steel strands (see Figure 13c). The measurements confirm that the replaceable energy-dissipating components yielded and dissipated energy during the reversed cyclic test, while the shear panel and the pre-stressed steel strands remained elastic throughout the imposed loading history. Provided that there are no considerable residual deformations within the composite MRF story, the energy-dissipating components of the beam-to-column connection can be easily replaced, which satisfies the resilience demand.

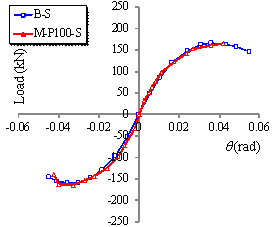
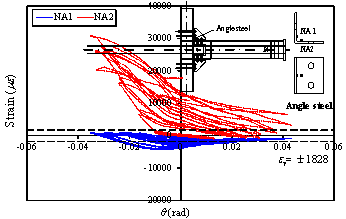
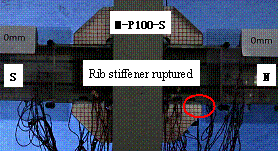4.2 Specimens tested under progressive collapse loading

4.2.1 Test results

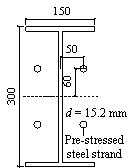
(A) Specimen B-C

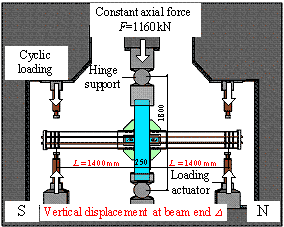
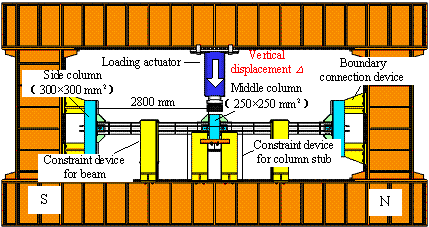
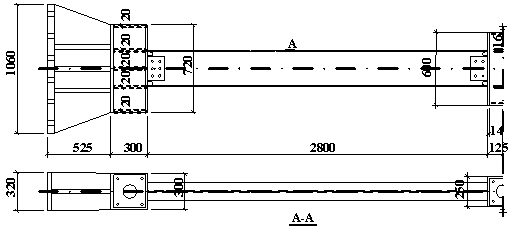
The maximum displacement of the middle column of Specimen B-C reached 250 mm, and the corresponding beam-to-column rotation angle was q = 0.089 rad. The overall deformation of the specimen after the test is shown in Figure 14.

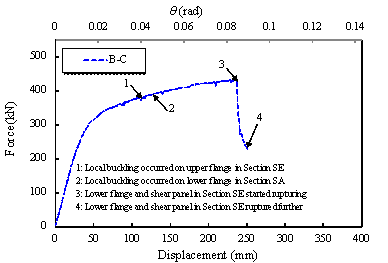
The load-displacement curve of the middle column of Specimen B-C is shown in Figure 15. The typical physical phenomena associated with the progression of damage are marked on the same figure and are illustrated in Figure 16:

(1)    Referring to Figure 16a, when D = 91 mm, local buckling occurred on the upper flange of the beam in Section SE (Figure 14). Considering the beam geometry and its material properties, the deformation level at which local buckling initiated is consistent with the predicted values in fully-restrained beam-to-column connections [48, 49].

(2)    From Figure 16b, local buckling occurred on the lower flange of the beam in Section SA (Figure 14) at a displacement D = 96 mm.

(3)    Fracture initiation at the lower flange and shear panel in Section SE occurred at a corresponding displacement D = 237 mm, indicating a peak force value of 431.6 kN.

(4)    Finally, at D = 250 mm, the joint lost more than 40% of its load carrying capacity due to progression of fracture of the lower flange and the shear panel in Section SE. At this point, the test was terminated.

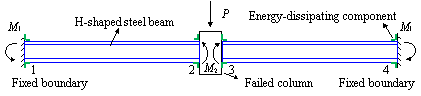
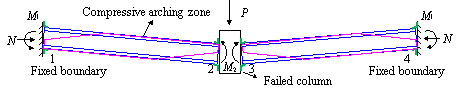
For Specimen B-C, due to the compressive arch action [50, 51] developed during the vertical loading process (Figure 17), the axial force in the beam increased, leading to the local buckling of the beam at q  = 0.033 rad. Similar local buckling phenomena were also found in the two progressive collapse tests of bolt-welded connection frame joints (Specimens SI-WB and SI-WB-2) conducted by Li et al. [52]. The dimensions of the beams in these two specimens (SI-WB and SI-WB-2), namely H300¡Á150¡Á6¡Á8, are very similar to those tested in this study. For Specimen B-S, the flange of the beam exhibited local buckling at q  = 0.019 rad. Nevertheless, such a local buckling was still undetectable until the angle reached 0.036 rad, which can be observed in Figures 10a and 10b. To sum up, the local buckling phenomena of Specimens B-S and B-C are considered conventional. In addition, the H-shaped steel beams adopted in Specimens B-S and B-C are scaled down from the prototype components in Building L. The width-thickness ratio of the beam flange meets the requirement of Article 8.4.2 of GB 50017-2017 [40], which satisfies the requirement for local stability of steel components. Additionally, according to the cyclic test results, the beam¡¯s moment resistance of Specimen B-S was greater than 80% of the beam¡¯s flexural strength at q  = 0.04 rad, which meets the requirement of AISC 341-16 [39] for composite special moment frames.

Figure 17 Compressive arch action in H-shaped steel beams at small deformation stage under concentrated load

(B) Specimen M-P100-C

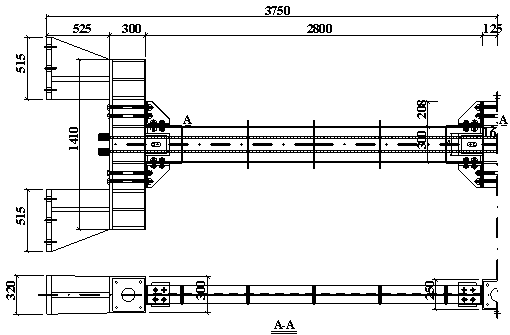
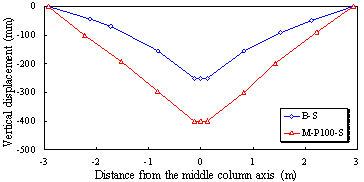
The maximum displacement of Specimen M-P100-C reached 399 mm, and the corresponding beam-column rotation angle was q = 0.143 rad. The overall deformation of the specimen after the test is shown in Figure 18. A comparison of the final vertical deformations of Specimen B-C and Specimen M-P100-C is shown in Figure 19. It is apparent that Specimen M-P100-C that employs the proposed beam-to-column configuration deformed nearly two times of Specimen B-S prior to connection failure. Therefore, the catenary action occurs more effectively. Note that catenary action is significant for progressive collapse design [53-55].

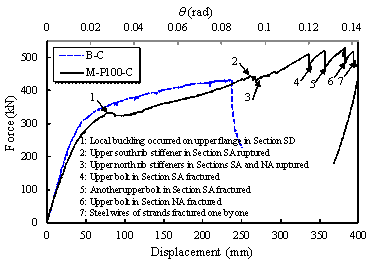
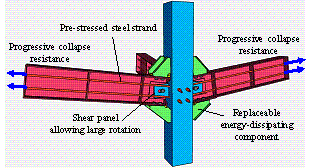
The physical phenomena corresponding to the damage initiation and progression of Specimen M-P100-C are depicted on the associated load-displacement curve of the middle column shown in Figure 20. Bending moments in Specimen M-P100-C are primarily provided by the energy-dissipating components and pre-stressed steel strands. Specifically, the energy-dissipating components can provide a steadily increasing bending moment [34]. 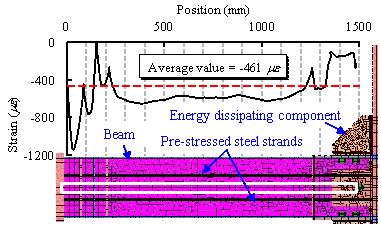The pre-stressed steel strands can provide the effective tying force and contribute to the catenary action. Figure 21 shows the axial forces in the pre-stressed steel strands in relation to the stages of load rebound of Specimen M-P100-C, which shows the characteristics different from that of Specimen B-C. These phenomena of Specimen M-P100-C are illustrated in Figure 22.

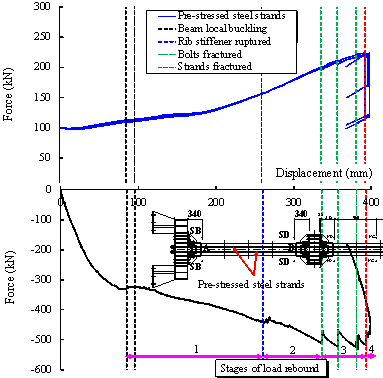
Figure 21 Axial force of pre-stressed steel strands and stages of load rebound of Specimen M-P100-C

In particular, when D = 85 mm (Point 1 on Figure 20), the steel beam experienced a local buckling on its upper flange at Section SD of the beam (see Figure 18). The external load of Specimen M-P100-C merely decreased from 332 kN to 321 kN. When 85 mm ¡Ü D < 260 mm, Specimen M-P100-C was in Stage 1 of load rebound (Figure 21). Note that Stage 1 represents the transition stage of the component from the compressive arch action [50, 51] (Figure 17) to the catenary action [53-55]. Because of the local buckling of the beam under the compressive arch action, the contribution of Specimen M-P100-C to the load resistance decreased. However, such a contribution provided by the steel strands due to the catenary action increased, which can be concluded from Figure 21. Additionally, Lu et al. [34] found that the energy-dissipating components can provide a steadily increasing load resistance. Therefore, the external load in Stage 1 of load rebound firstly decreased and then increased.

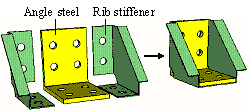
Referring to Figure 22b, despite the fact that the upper south rib stiffener in Section SA (Figure 18) ruptured at D = 260 mm (Point 2 on Figure 20), the specimen¡¯s resistance decreased slightly (from 443 kN to 430 kN) due to force redistributions occurring within the beam-to-column joint. Similarly, (D = 270 mm) the upper north rib stiffeners in Sections SA and NA ruptured (see Figure 22c) and the specimen¡¯s resistance further decreased (from 442 kN to 424 kN). When 260 mm ¡Ü D < 336 mm, Specimen M-P100-C was in Stage 2 of load rebound (Figure 21). In this stage, the steel strands (Figure 21) and the angle steels of the energy-dissipating components can provide a steadily increasing resistance [34]. Therefore, the external load declined for a short time and then continued to rise.

Notably, due to the catenary action, the specimen was able to sustain more load up to a vertical displacement D = 336 mm (Point 4 on Figure 20) and then one of the upper bolts in Section SA fractured (see Figure 22d). Referring to Figure 20, at this point, the specimen¡¯s resistance was instantaneously dropped from 510 kN to 469 kN. However, the specimen was still able to redistribute the load, albeit bolt fractures continued in the connections in Sections SA (see Figure 22e) and NS (see Figure 22f). These are associated with Points 5 (D = 357 mm) and 6 (D = 381 mm), respectively, in Figure 20. When 336 mm ¡Ü D < 393 mm, Specimen M-P100-C was in Stage 3 of load rebound (Figure 21). It can be seen from Figure 21 that the fracture of the bolts had little influence on the steel strands. The steel strands were still able to provide a steadily increasing resistance, and served to provide the catenary action ensuring the stability of the structural strength. Therefore, the external load rebounded in this stage.

Finally, the specimen lost its load carrying capacity at D = 393 mm because of consecutively fractured steel tendons in the pre-stressed steel strands. This is shown in Figure 22g. When 393 mm ¡Ü D < 399 mm, Specimen M-P100-C was in Stage 4 of load rebound (Figure 21). When one of the strands was broken, the remaining unbroken strands were not affected and could still provide a steadily increasing resistance (Figure 21). With the increase of the beam-to-column connection angle, the vertical force provided by the steel strands would increase. Therefore, the external load also rebounded in this stage.

In order to ensure the safety of the test, the test was terminated at D = 399 mm.

According to the DoD guidelines [40], Specimen B-C complies with the case of welded unreinforced flange-bolted web (WUF-B). The failure plastic rotation angle a and the ultimate plastic rotation angle b of Specimen B-C can be obtained by subtracting the yield rotation angle (0.0062 rad determined by the DoD guidelines [40]) from the angles of the different critical states. The failure plastic rotation angle a of Specimen B-C was 0.078 rad and the ultimate plastic rotation angle b of Specimen B-C was larger than 0.083 rad, which are much larger than the limits specified in the DoD guidelines [41] (a = 0.016 rad, b = 0.043 rad). The deformation capacity and strength of Specimen M-P100-C are significantly better than those of Specimen B-C, i.e., the rotational ductility of Specimen M-P100-C was 59.6% higher than that of Specimen B-C and the strength of Specimen M-P100-C was 22.6% higher than that of Specimen B-C. In conclusion, SPCRCF has remarkably larger progressive collapse resistance.

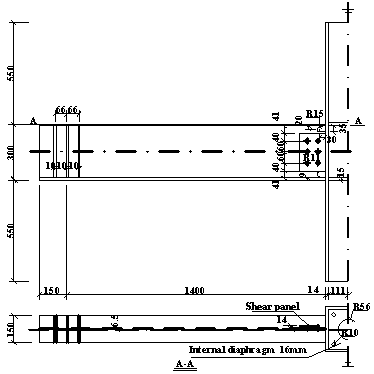
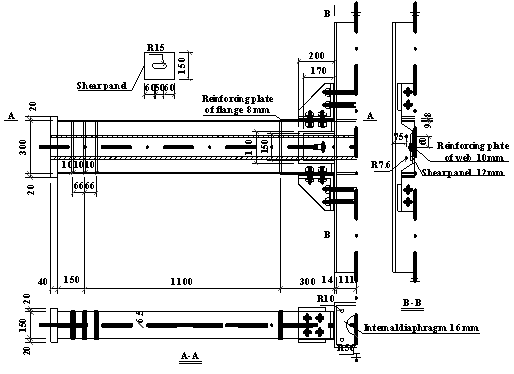
4.2.2 Description of failure mechanism

This section intends to describe key findings associated with differences in the failure mechanisms observed in Specimens B-C and M-P100-C. For this reason, measurements from strain gauges installed in characteristic cross-sections are fully correlated with the measured force-displacement relationships of the specimens. Note that above a certain strain threshold, the strain gauge measurements are only indicative of the load redistributions occurring within the specimen.

(A) Specimen B-C

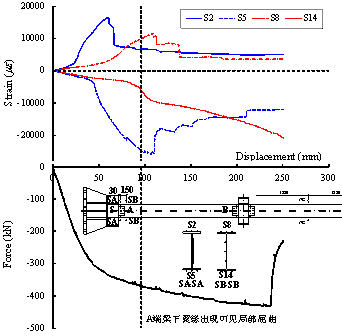
Figure 23 shows the engineering strain development at four different locations (S2, S5, S8 S14), in the longitudinal direction in Sections SA and SB of the steel beam. From this figure it is apparent that during loading the upper beam flange in Sections SA and SB was always in tension while the beam¡¯s lower flange was always in compression, as expected. Local buckling occurred on the compression flange when D = 91 mm, thereby releasing the compressive arch action. Thus, there was a slight decrease in the measured strains of the beam flange (S2, S5, and S8). Strain S14 increased after beam flange local buckling occurred because Section SB was located within buckled region. Note that measurements after 3000 ¦Ì¦Å are only indicative and depict the force re-distributions. Similar observations hold true from measurements within Sections SD, SE, NA, NB, ND, and NE of the B-C specimen. The measurements also confirm that after fracture of the lower flange and the shear panel (Section SE), the CFST columns remained elastic.

(B) Specimen M-P100-C

Figure 24 shows the progression of the engineering strains extracted from nominally identical cross-sections (Sections SB and SD) with Specimen B-C. In the same figure, the strain measurements are synchronized with the applied load at Specimen M-P100-C. From this figure, the top beam flange stayed always in tension, while the lower beam flange stayed always in compression, thereby experiencing local buckling in Section SD at D = 85 mm. After that, the compressive arch action was released. Local buckling caused load redistribution within the subassembly, which resulted in a slight strain decrease of the flange in Section SD based on the measured strains from S20 and S26. Because the local buckling was mainly located in Section SD, the strain of the flange in Section SB changes more smoothly.

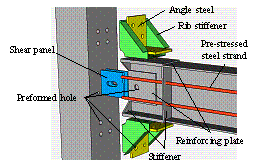
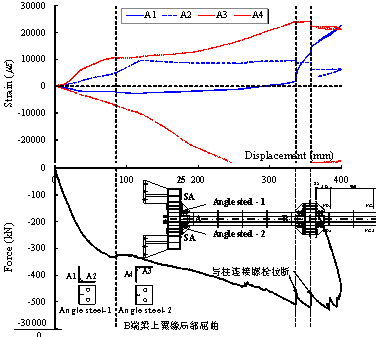
Referring to Figure 25, supplemental strain measurements were conducted in this case at a cross-section (noted as Section SA) of the angle steel. Four locations were monitored (noted as A1, A2, A3 and A4), which are also shown in the same figure. During the loading process, the strains were always compressive at locations A1 and A3, as expected. Similarly, the strain measurements at locations A2 and A4 were tensile due to the flexural-tensile deformation of the angle steel. From Figure 25, while the vertical displacement increased, Strain A1 gradually switched from compression to tension. After the fracture of the bolt occurred in Angle steel-1, the lever arm on the column leg of Angle steel-1 increased, thereby causing larger tensile strains at location A1.

5. Numerical simulation

Based on the experimental data, the finite element models of Specimens B-S, M-P100-S, B-C, and M-P100-C were developed using the general-purpose nonlinear finite element software, MSC.Marc [33]. All the components were modeled using solid elements. Considering that there was no yield in the CFST column, elastic material was adopted to model the column. Contact algorithm was adopted among different components of the finite element models, which was consistent with the actual situation. The pre-stressed forces in the bolts and strands were modeled by the temperature stress. The initial geometric imperfections of the beams and the rib stiffeners were simulated using the method proposed in Eurocode 3 [56] and GB 50017-2017 [40]. The components gradually failed during the tests, which could be simulated using the elemental deactivation technique. The UACTIVE subroutine of MSC.Marc 2007 was adopted to deactivate the element when its strain reached the material failure strain [57].

5.1 Seismic cyclic test specimens

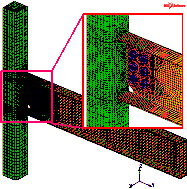
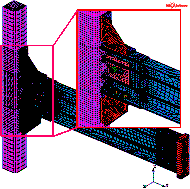
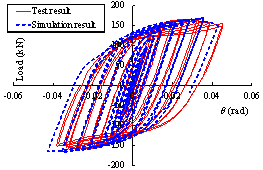
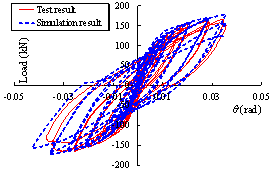
The finite element models of Specimens B-S and M-P100-S are shown in Figure 26. The comparisons between the simulation and test results are shown in Figure 27. The comparisons show that the finite element models established based on the above method can accurately simulate the response of the specimens under cyclic loading.

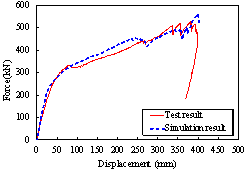
5.2 Progressive collapse test specimens

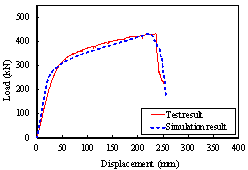
The comparisons between the simulation and test results of Specimens B-C and M-P100-C are shown in Figure 28. The comparisons show that the finite element models established based on the above method can accurately simulate the progressive collapse response of the structures under the middle column-removal scenario.

6. Conclusions

Comprehensive defense of seismic action and progressive collapse is a new frontier for civil engineering practice. To improve the seismic and progressive collapse resistant performance of a steel-concrete composite frame structure, an SPCRCF was proposed in this work. Seismic and progressive collapse performances of the conventional frame and the proposed SPCRCF were compared through experiments, and the test specimens were simulated using general-purpose finite element software. The following conclusions are drawn from this work.

(1) The initial stiffness and strength of the proposed SPCRCF (Specimen M-P100-S) under cyclic loading were similar to those of the conventional frame (Specimen B-S). In addition, Specimen M-P100-S demonstrated less damage and smaller residual deformation compared with Specimen B-S. Therefore, the proposed SPCRCF exhibited significantly better seismic resilience.

(2) In the middle column-removal scenario, the proposed SPCRCF (Specimen M-P100-C) exhibited the catenary action, provided a better resistance and achieved a larger rotational capacity at the beam-column connection, leading to enhanced deformation capacity and resistance, as well as a higher safety margin compared with the conventional frame (Specimen B-C). Therefore, the proposed SPCRCF yielded better progressive collapse performance.

(3) The finite element models proposed in this work simulated the load-displacement responses accurately under both earthquake ground motions and a middle column-removal scenario.

In summary, the proposed SPCRCF is proven to have more seismic resilience and higher progressive collapse resistance than the conventional steel-concrete composite frame.

Acknowledgement

This work was supported by Beijing Natural Science Foundation [8182025]. The authors also thank Prof. Dimitrios Lignos of EPFL for his constructive suggestions on this paper.

References

[1]      Nethercot D, Vidalis C. Improving the resistance to progressive collapse of steel and composite moment frames. Structures Congress 2015; pp. 1138-1149. https://doi.org/10.1061/9780784479117.097.

[2]      Adaros MS, Smilowitz R. Challenges and considerations for the retrofit of existing structures for progressive collapse. Journal of Performance of Constructed Facilities 2014; 29(5):B4014001. https://doi.org/10.1061/(ASCE)CF.1943-5509.0000675.

[3]      Hajjar JF. Composite steel and concrete structural systems for seismic engineering. Steel Construction 2008; 58(5):703-723. https://doi.org/10.1016/S0143-974X(01)00093-1.

[4]      Mehanny SSF, Deierlein GG. Seismic damage and collapse assessment of composite moment frames. Journal of Structural Engineering 2001; 127(9):1045-1053. https://doi.org/10.1061/(ASCE)0733-9445(2001)127:9(1045).

[5]      Hajjar JF, Leon RT, Gustafson MA, Shield CK. Seismic response of composite moment-resisting connections. II: behavior. Journal of Structural Engineering 1998; 124(8):868-876. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:8(877).

[6]      Ministry of Housing and Urban-Rural Development of the People's Republic of China (MOHURD). Code for design of composite structures (JGJ 138-2016). Beijing: China Architecture & Building Press; 2016. (in Chinese).

[7]      China Association for Engineering Construction Standardization (CECS). Code for anti-collapse design of building structures. Beijing: China Planning Press; 2014. (in Chinese).

[8]      National Institute of Standards and Technology (NIST). Evaluation of the FEMA P-695 methodology for quantification of building seismic performance factors. National Institute of Standards and Technology, Gaithersburg, Maryland; 2010.

[9]      British Standard Institute (BSI). BS EN 1994-1-1. 2004 Eurocode 4: Design of composite steel and concrete structures, Part 1-1: general rules and rules for buildings. CEN Central Secretariat, Rue de Stassart 36, B-1050; 2004.

[10]  Fascetti A, Kunnath SK, and Nistic¨° N. Robustness evaluation of RC frame buildings to progressive collapse. Engineering Structures 2015; 86:242-249. https://doi.org/10.1016/j.engstruct.2015.01.008.

[11]  Khalili-Tehrani P, Masroor A, Dogruel S, Cormie D, Gallo M, Almufti. Lessons learned from the design of steel and RC structures against progressive collapse using nonlinear alternate path analysis. Structures Congress 2014; pp. 954-965. https://doi.org/10.1061/9780784413357.085.

[12]  Li Y, Ahuja A, Padgett JE. Review of methods to assess, design for, and mitigate multiple hazards. Journal of Performance of Constructed Facilities 2011; 26(1):104-117. https://doi.org/10.1061/(ASCE)CF.1943-5509.0000279.

[13]  Lin KQ, Li Y, Lu XZ, Guan H. Effects of seismic and progressive collapse designs on the vulnerability of RC frame structures. Journal of Performance of Constructed Facilities 2016; 31(1):04016079. https://doi.org/10.1061/(ASCE)CF.1943-5509.0000942.

[14]  Lopez-Barraza A, Ruiz SE, Reyes-Salazar A, Boj¨®rquez E. Demands and distribution of hysteretic energy in moment resistant self-centering steel frames. Steel & Composite Structures 2016; 20(5):1155-1171. http://dx.doi.org/10.12989/scs.2016.20.5.1155.

[15]  Rojas P, Ricles JM, Sause R. Seismic performance of post-tensioned steel moment resisting frames with friction devices. Journal of Structural Engineering 2005; 131(4):529-540. https://doi.org/10.1061/(ASCE)0733-9445(2005)131:4(529).

[16]  Christopoulos C, Filiatrault A, Uang CM, Folz B. Posttensioned energy dissipating connections for moment-resisting steel frames. Journal of Structural Engineering 2002; 128(9):1111-1120. https://doi.org/10.1061/(ASCE)0733-9445(2002)128:9(1111).

[17]  Garlock MM, Ricles JM, Sause R. Influence of design parameters on seismic response of post-tensioned steel MRF systems. Engineering Structures 2008; 30(4):1037-1047. https://doi.org/10.1016/j.engstruct.2007.05.026.

[18]  Ricles JM, Sause R, Peng SW, Lu LW. Experimental evaluation of earthquake resistant posttensioned steel connections. Journal of Structural Engineering 2002; 7(7):850-859. https://doi.org/10.1061/(ASCE)0733-9445.

[19]  Wang W, Fang C, Liu J. Self-centering beam-to-column connections with combined superplastic SMA bolts and steel angles. Journal of Structural Engineering 2016; 143(2):04016175. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001675.

[20]  Wang W, Chan TM, Shao HL, Chen YY. Cyclic behavior of connections equipped with NiTi shape memory alloy and steel tendons between H-shaped beam to CHS column. Engineering Structures 2015; 88:37-50. https://doi.org/10.1016/j.engstruct.2015.01.028.

[21]  Kim HJ, Christopoulos C. Friction damped posttensioned self-centering steel moment-resisting frames. Journal of Structural Engineering 2008; 134(11):1768-1779. https://doi.org/10.1061/(ASCE)0733-9445(2008)134:11(1768).

[22]  Zhang AL, Zhang YX, Li R, Wang ZY. Cyclic behavior of a prefabricated self-centering beam¨Ccolumn connection with a bolted web friction device. Engineering Structures 2016; 111:185-198. https://doi.org/10.1016/j.engstruct.2015.12.025.

[23]  Guo T, Song LL, Zhang GD. Numerical simulation and seismic fragility analysis of self-centering steel MRF with web friction devices. Journal of Earthquake Engineering 2015; 19(5):731-751. https://doi.org/10.1080/13632469.2014.1003437.

[24]  Eatherton MR, Ma X, Krawinkler H, Mar D, Billington S, Hajjar JF, Deierlein GG. Design concepts for controlled rocking of self-centering steel-braced frames. Journal of Structural Engineering 2014; 140(11):04014082. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001047.

[25]  Vasdavellis G, Baiguera M, AI-Sammaraie D. Numerical simulation of the progressive collapse behaviour of steel self-centering moment resisting frames. 8th International Conference on Steel and Aluminium Structures, Hong Kong, China; 2016.

[26]  Pirmoz A, Liu M. Finite element modeling and capacity analysis of post-tensioned steel frames against progressive collapse. Engineering Structures 2016; 126:446-456. https://doi.org/10.1016/j.engstruct.2016.08.005.

[27]  Rousakis TC, Panagiotakis GD, Archontaki EE, Kostopoulos AK. Prismatic RC columns externally confined with FRP sheets and pretensioned basalt fiber ropes under cyclic axial load. Composites Part B: Engineering 2019; 163:96-106. https://doi.org/10.1016/j.compositesb.2018.11.024.

[28]  Rousakis TC. Inherent seismic resilience of RC columns externally confined with nonbonded composite ropes. Composites Part B: Engineering 2018; 135:142-148. https://doi.org/10.1016/j.compositesb.2017.10.023.

[29]  Rousakis TC. Hybrid confinement of concrete by fiber-reinforced polymer sheets and fiber ropes under cyclic axial compressive loading. ASCE, Journal of Composites for Construction 2013; 17(5):732-43. https://doi.org/10.1061/(ASCE)CC.1943-5614.0000374.

[30]  Fakharifar M, Chen G, Sneed L, Dalvand A. Seismic performance of post-mainshock FRP/steel repaired RC bridge columns subjected to aftershocks. Composites Part B: Engineering 2015; 72:183-198. https://doi.org/10.1016/j.compositesb.2014.12.010.

[31]  Kwon M, Seo H, Kim J. Seismic performance of RC-column wrapped with Velcro. Structural Engineering & Mechanics 2016; 58(2):379-395. https://doi.org/10.12989/sem.2016.58.2.379.

[32]  Echevarria A, Zaghi AE, Christenson R, Accorsi M. CFFT bridge columns for multihazard resilience. Journal of Structural Engineering 2016; 142(8):C4015002. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001292.

[33]  MSC. Software Corp. MSC. Marc user¡¯s manual. MSC. Software Corporation, Santa Ana, CA; 2007.

[34]  Lu XZ, Zhang L, Cui Y, Li Y, Ye LP. Experimental and theoretical study on a novel dual-functional replaceable stiffening angle steel component. Soil Dynamics and Earthquake Engineering 2018; 114:378-391. https://doi.org/10.1016/j.soildyn.2018.07.040.

[35]  Yang XM, Xu HC, Zhen W, Bao LJ. Structural seismic design of Luoyang Zhengda ultra-limit high-rise office building. Building Structure 2013; 18:39-43. (in Chinese). https://doi.org/10.19701/j.jzjg.2013.18.008.

[36]  Ministry of Housing and Urban-Rural Development of the People's Republic of China (MOHURD). Code for seismic design of buildings (GB50011-2010). Beijing: China Architecture & Building Press; 2010. (in Chinese).

[37]  Lu XZ, Li MK, Guan H, Lu X, Ye LP. A comparative case study on seismic design of tall RC frame-core tube structures in China and USA. The Structural Design of Tall and Special Buildings 2015; 24:687-702. 10. https://doi.org/10.1002/tal.1206.

[38]  American Society of Civil Engineers (ASCE). Minimum design loads and associated criteria for buildings and other structures, ASCE/SEI 7-16, Reston, VA; 2016.

[39]  American Institute of Steel Construction (AISC). Seismic provisions for structural steel buildings. ANSI/AISC 341-16, Chicago; 2016.

[40]  Ministry of Housing and Urban-Rural Development of the People's Republic of China (MOHURD). Standard for classification of steel structures (GB 50017-2017). Beijing: China Architecture & Building Press; 2017. (in Chinese).

[41]  Department of Defense (DoD). Design of structures to resist progressive collapse. Unified facility criteria, UFC 4-023-03, Washington, DC; 2016.

[42]  Zhang AL, Zhang YX, Li R, Wang ZY. Cyclic behavior of a prefabricated self-centering beam-column connection with a bolted web friction device. Engineering Structures 2016; 111:185-198. https://doi.org/10.1016/j.engstruct.2015.12.025.

[43]  Standardization Administration of the People¡¯s Republic of China (SAC). Metallic materials - Tensile testing - Part l: Method of test at room temperature (GB/T 228.1 - 2010). Beijing: China Zhijian Publishing House; 2010. (in Chinese).

[44]  Ministry of Housing and Urban-Rural Development of the People's Republic of China (MOHURD). Technical specification for concrete structures prestressed with unbonded tendons (JGJ 92-2016). Beijing: China Architecture & Building Press; 2016. (in Chinese).

[45]  American Concrete Institute (ACI). 550.3-13. Design specification for unbonded post tensioned precast concrete special moment frames satisfying ACI 374.1 and commentary, Farmington Hills, MI; 2013.

[46]  Mattock AH. Flexural strength of prestressed concrete sections by programmable calculator. PCI Journal 1979; 885-886. https://doi.org/10.15554/pcij.01011979.32.54.

[47]  Federal Emergency Management Agency (FEMA). Seismic performance assessment of buildings volume 1-methodology, FEMA P-58. Federal Emergency Management Agency, Washington, DC; 2012.

[48]  Lignos DG, Krawinkler H. Development and utilization of structural component databases for performance-based earthquake engineering. Journal of Structural Engineering 2013; 139(8):1382-1394. https://doi.org/10.1061/(ASCE)ST.1943-541X.0000646.

[49]  Lignos DG, Krawinkler H. Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. Journal of Structural Engineering 2011; 137(11):1291-1302. https://doi.org/10.1061/(ASCE)0733-9445(2002)128:4(420).

[50]  Lu XZ, Lin KQ, Li CF, Li Y. New analytical calculation models for compressive arch action in reinforced concrete structures. Engineering Structures 2018; 168:721-735. https://doi.org/10.1016/j.engstruct.2018.04.097.

[51]  Kang SB, Tan KH. Analytical model for compressive arch action in horizontally restrained beam-column subassemblages. ACI Structural Journal 2016; 113(4):813-826. https://doi.org/10.14359/51688629.

[52]  Ling L, Wei W, Chen Y, Lu Y. Effect of beam web bolt arrangement on catenary behaviour of moment connections. Steel Construction 2015; 104(104):22-36. https://doi.org/10.1016/j.jcsr.2014.09.016.

[53]  Li Y, Lu XZ, Guan H, Ye LP. Progressive collapse resistance demand of RC frames under catenary mechanism. ACI Structural Journal 2014; 111(5):1225-1234. https://doi.org/10.14359/51686809.

[54]  Li Y, Lu XZ, Guan H, Ye LP. An improved tie force method for progressive collapse resistance design of reinforced concrete frame structures. Engineering Structures 2011; 33(10):2931-2942. https://doi.org/10.1016/j.engstruct.2011.06.017.

[55]  Guo LH, Gao S, Fu F, Wang YY. Experimental study and numerical analysis of progressive collapse resistance of composite frames. Journal of Constructional Steel Research 2013; 89(5):236-251. https://doi.org/10.1016/j.jcsr.2013.07.006.

[56]  British Standard Institute (BSI). BS EN 1993-1-1. 2005 Eurocode 3: Design of steel structures, Part 1-1: general rules and rules for buildings. CEN Central Secretariat, Rue de Stassart 36, B-1050; 2005.

[57]  Lu X, Lu XZ, Guan H, Ye LP, Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes. Earthquake Engineering & Structural Dynamics 2013; 42(5):705-723. https://doi.org/10.1002/eqe.2240.