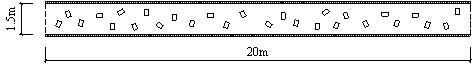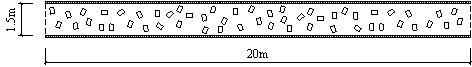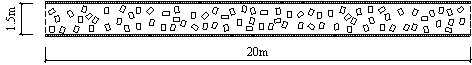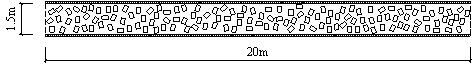1 Introduction

Buildings and populations are being concentrated rapidly in urban areas (UN-Habitat, 2016), and are facing multiple risks once an earthquake occurs (Yamazaki et al., 2005; Zhao et al., 2009; Mousavi et al., 2008; Xu et al., 2016; Yang et al., 2015). The collapse resistances of buildings have been continuously improved in recent years (Lu et al., 2013; Li et al., 2014). However, the damage of non-structural components is still severe. In consequence, a large number of falling debris-induced casualties occurred in past earthquakes (Peek-Asa et al., 1998; Chan et al., 2006; Qiu et al., 2010). Moreover, falling debris will cover the roads and hindered the pedestrian movement in densely built-up areas (Goretti & Sarli, 2006; Hirokawa & Osaragi, 2016). Pedestrian evacuation to emergency shelters will be blocked by the falling debris, and the evacuation velocity will also be reduced (D¡¯Orazio et al., 2014; Bernardini et al., 2016). Therefore, the influence of falling debris needs to be considered in earthquake evacuation, and two corresponding key issues need to be addressed: (1) How to predict the falling debris distribution; (2) How to model the influence of falling debris distribution on the pedestrian movement.

There are some existing studies about the falling debris of non-structural components induced by earthquakes. Liu et al. (2015) analyzed the debris of indoor partition walls and suspended ceilings based on the fragility curves of non-structural components. In their work, falling debris of non-structural components was assumed to cover the floor evenly and completely. Cimellaro et al. (2017) assumed the hazard ranges of existing obstacles during an earthquake. Satellite photographs were also utilized to identify building damage and outdoor debris distribution (Saito et al., 2004; Quagliarini et al., 2016). For example, on the basis of satellite images, Quagliarini et al. (2016) proposed ruins formation models using regression method, where ruins were assumed to uniformly distribute along the street. However, collision and motion of falling debris after hitting the ground are seldom considered in the aforementioned literature. Moreover, in the real world, the falling debris of non-structural components isn¡¯t uniformly distributed. As a result, there is no suitable model to predict the distribution of falling debris of non-structural components.

Many factors need to be considered in pedestrian evacuation simulation after an earthquake. Xiao et al. (2016) adopted social force model to implement the evacuation simulation and proposed safety escape time criteria. Wijerathne et al. (2013) conducted pedestrian evacuation in a city, which investigated the behavior of human with different familiar extents. Osaragi et al. (2014) studied the roads covered by collapsed buildings and the influence of fire following earthquake, and also evaluated the risk areas during evacuation. D¡¯Orazio et al. (2014) proposed human behavior model through analyzing human behaviors in earthquakes, in which the influence of debris induced by collapsed buildings was also included. Note that during the outdoor evacuation, people will encounter areas covered by debris. Existing studies mostly focus on the influence of debris caused by building collapse, while the studies of falling debris induced by non-structural components are limited (Alexander 1990). Neglecting the falling debris of non-structural components will underestimate their influence on evacuation. Meanwhile, the assumption that people can¡¯t pass through the areas covered by some falling debris will overestimate the influence of falling debris on evacuation (Quagliarini et al., 2016). Particularly, if the roads are assumed to be entirely blocked due to the overestimation of falling debris influence, the predicted evacuation process and total time will be significantly changed.

Therefore, it¡¯s necessary to study the distribution of the falling debris of non-structural components under an earthquake, quantify the influence of debris on pedestrians¡¯ velocity, investigate the evacuation process in the scenario with debris, and identify areas with high risk during the outdoor evacuation. In this work, a framework of regional evacuation simulation considering falling debris is proposed. Subsequently, the methodology to predict the distribution of falling debris of masonry infilled wall is proposed through experimental and numerical simulations. Furthermore, the influence of debris distribution on pedestrian movement is quantified through experiment. Finally, the teaching area in Tsinghua University campus is selected as a case to demonstrate the proposed frame herein, and post-earthquake evacuation simulation is conducted. The influence of falling debris on evacuation is analyzed, and roads with high risk are identified.

2 Methodology

2.1 Framework of pedestrian evacuation simulation

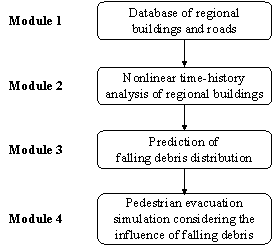
As shown in Figure 1, the proposed framework consists of four modules: (1) Database of regional buildings and roads; (2) Nonlinear time-history analysis of regional buildings; (3) Prediction of falling debris distribution; (4) Pedestrian evacuation simulation considering the influence of falling debris.

Figure 1 The proposed framework of pedestrian evacuation simulation

Module 1: Database of regional buildings and roads

GIS platform is employed to store and organize building and road information, which will provide the necessary data for seismic response analysis and evacuation scenario construction.

Module 2: Nonlinear time-history analysis of regional buildings

Nonlinear time-history analysis of regional buildings will provide the necessary data for the prediction of falling debris distribution. Multi-degree-of-freedom (MDOF) shear model and MDOF flexural-shear model proposed by Xiong et al. (2016, 2017) will be adopted due to their accuracy and efficiency. Time histories of the displacement and velocity on each story of each building are then obtained.

Module 3: Prediction of falling debris distribution

Nonstructural components such as masonry infilled walls will crack and induce falling debris when exceed their failure criteria (ASCE, 2010; Xu et al., 2016). The falling debris will collide the ground and jump to a certain range. The general finite element (FE) code LS-DYNA (LSTC, 2014) is chosen to simulate the movement of falling debris, based on which the distribution of debris can be predicted.

Module 4: Pedestrian evacuation simulation considering the influence of falling debris

Based on the database in Module 1, the locations of buildings and emergency shelters, the road information and the population in each building can be determined. According to the results in Modules 2 and 3, regions covered by falling debris are established in the evacuation scenario. Considering the velocity reduction when people pass through the area covered by falling debris, social force model (Helbing & Molnar, 1995) is adopted to perform the pedestrian evacuation simulation.

Details of the above four modules are introduced one-by-one in the following sections.

2.2 Database of regional buildings and roads

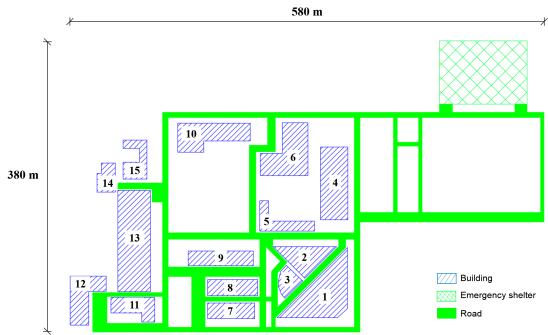
Database of regional buildings and roads are the basis of building response analysis and evacuation scenario construction. Building information, road information, emergency shelter location and population distribution are contained in the database, which are stored and organized in a GIS platform. Here, a widely used commercial software ArcGIS is employed as the GIS platform (Dong et al., 2012; Karimzadeh et al., 2014; Lu et al., 2014). Attribute data of buildings such as building height, occupancy, number of stories, structural type, construction year, planar area can be obtained through city database (Xiong et al., 2015) or field investigation (Zeng et al., 2016). The location of buildings and emergency shelters, as well as the information of roads, can be obtained from various resources such as Google Map (Wu et al., 2007) or OpenStreetMap (Haklay & Patrick, 2008). Population in each building should also be confirmed during the evacuation simulation. FEMA P-58 provides the building population models, which define the number of people per 1000 square feet of building floor area with different occupancies (FEMA, 2012). Consequently, the population in each building can be predicted using FEMA P-58 and building attribute data.

2.3 Nonlinear time-history analysis of regional buildings

Nonlinear time-history analysis of regional buildings provides necessary data for falling debris distribution prediction. There are large amounts of buildings in an urban region, and detailed information like construction drawings is hard to acquire. Moreover, conventional FE analysis will result in an enormous workload, which isn¡¯t applicable in urban seismic simulation. In order to overcome the aforementioned challenges and achieve satisfactory computational accuracy and efficiency, Xiong et al. (2016, 2017) proposed the nonlinear MDOF models (including the nonlinear MDOF shear model for multi-story frame structures and masonry structures, and the nonlinear MDOF flexural-shear model for tall buildings) to simulate the buildings in an urban region. Based on the corresponding design codes and massive experimental data, Xiong et al. (2016, 2017) proposed the methodology to determine the parameters of the nonlinear MDOF models, with which all parameters (e.g., inter-story stiffness, yield and peak strengths and drift ratios) in the nonlinear MDOF models can be determined by using attribute data of buildings in the GIS platform only (i.e. building height, number of stories, structural type, construction year, functionality and planar area). Subsequently, nonlinear MDOF models of regional buildings are established, and seismic response results (e.g., the time history results of the displacement and velocity on each story) can be obtained through nonlinear time-history analysis.

2.4 Prediction of falling debris distribution

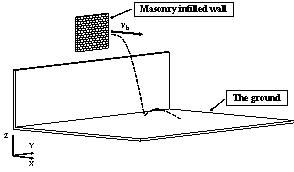
Masonry infilled walls are widely used as exterior building envelope. Previous seismic damage investigations indicated that: masonry infilled wall could be severely damaged during an earthquake (Dizhur et al., 2011; Miranda et al., 2012), and roads could be covered by the falling bricks of masonry infilled walls. Therefore, masonry infilled wall is selected in this work as a typical example to study the falling debris distribution. The prediction of falling debris distribution of infilled walls includes three parts: (1) Falling criteria of infilled walls; (2) Spatial motion of falling bricks; (3) Motion after hitting the ground and the final distribution of bricks.

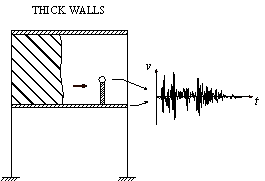
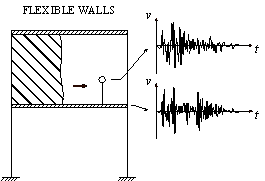
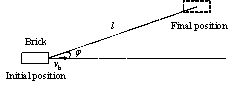
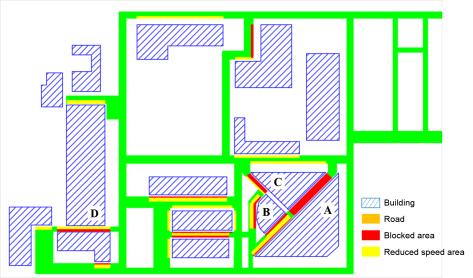
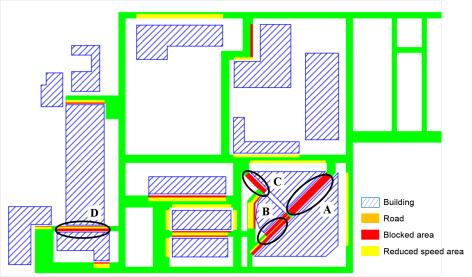
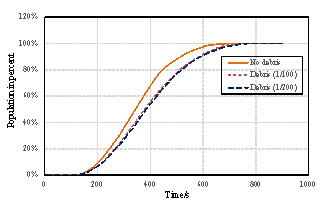
The nonlinear time-history analysis of each building in Module 2 will generate the time-history of drift ratios on each story. According to ASCE-07 (ASCE, 2010), the failure of masonry infilled walls is controlled by drift ratio. Existing studies found that the corresponding drift ratio limits of infilled wall failure range from 1/143 to 1/50 (ASCE, 2010). For example, Restrepo & Bersofskyb (2011) conducted quasi-static cyclic tests of 8 infilled walls, and the failure drift ratios ranged from 1/200 to 1/33. Belleri et al. (2016) investigated the seismic performance of cladding panels. The drift ratio when the cladding panels failed ranged from 1/100 to 1/48 due to the difference in connections. These works show that the drift ratio limit corresponding to infill wall failure has considerable deviation. Consequently, in this work, in order to consider the uncertainty of infill wall failure, two drift ratio limits (i.e. D_fall = 1/100, D_fall = 1/200) are selected for parametric discussion. The debris distribution and pedestrian evacuation subjected to these two limits are calculated, respectively. Infilled walls can be divided into two types: (1) thick walls and (2) flexible walls (Kaushik et al., 2006; Lee et al., 2007). Thick walls move simultaneously with the attached floor (Figure 2(a)), while the bricks of the flexible walls have different velocity time-histories from the floor (Figure 2(b)). Due to the thermal performance requirement, most Chinese buildings have thick envelop walls. Consequently, only thick walls are considered in this work. When the infilled wall fails, bricks are assumed to undergo a horizontal projectile motion (Xu et al., 2016). The initial velocity of the falling bricks equals to the floor velocity at the moment of failure.

Figure 2 Simplified models of two types of infilled walls

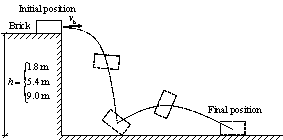
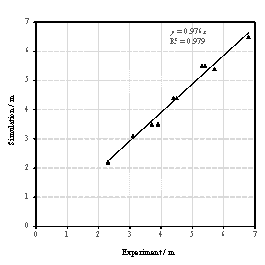
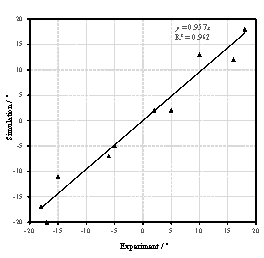
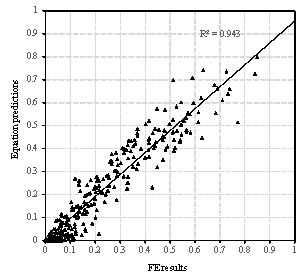
Note that when the bricks hit the ground, the bricks will jump again and move in a certain range. Therefore, the final positions of bricks are different from their first landing positions. Motions of the bricks after hitting the ground haven¡¯t been considered or modeled in existing studies (Xu et al., 2016; Quagliarini et al., 2016). Hence, this work studied the motion of bricks after hitting the ground. Specifically, brick falling experiment was conducted first, in which bricks were thrown horizontally from three different heights, and the final positions of bricks were recorded. Next, the movements of bricks in the brick falling experiment were simulated using FE analysis to validate the reliability of the FE model and parameters in the FE analysis. After that, the falling behaviors of masonry infilled wall from different heights were repeatedly simulated with different initial horizontal velocities using the validated FE model. Finally, the percentages of areas covered by bricks on the ground were counted, and the models to prediction the falling debris distribution were obtained through regression. This methodology is one of key contributions of this study, which will be presented in detail in Section 3. Based on the nonlinear time-history results of buildings and the falling debris distribution models, the hazard ranges of debris and the percentage of the road surface covered by debris can then be predicted.

2.5 Pedestrian evacuation simulation considering the influence of falling debris

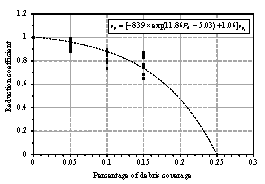
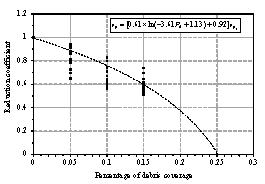
The pedestrian evacuation simulation considering the influence of falling debris consists of two parts: evacuation environment construction and human behavior modeling. Building locations, road information, emergency shelter locations and the number of people in the evacuation environment can be determined according to the database in Module 1, where debris distribution on the road can be determined according to Module 3. As for human behavior, cellular automaton, network model and social force model are the most widely used models in evacuation simulation (Duives et al., 2013). Social force model is a microscopic model, which is able to consider various crowd self-organization phenomena. This model has been well validated by real evacuation events (Johansson et al., 2008; Li et al., 2015). Consequently, it is widely employed in evacuation simulation (Parisi et al., 2009; Wan et al., 2014; Xiao et al., 2016). In this work, social force model is also adopted to conduct the evacuation simulation. The pedestrian evacuation scenario is generated in this work using the evacuation simulation software of Viswalk (Henningsson & Blomstrand, 2015; PTV, 2016). For areas without debris, pedestrians pass through with normal velocity. By contrast, for areas covered by debris, the velocity of pedestrians will change, which has a significant influence on the evacuation process. Some literature assumed that pedestrian can¡¯t pass through the areas covered by debris (Liu et al., 2015; Cimellaro et al., 2017), which may overestimate the evacuation time. In order to investigate the influence of falling debris on the pedestrian velocity, pedestrian movement experiment with different percentages of debris coverage were designed in this work, in which four scenarios were set (i.e., debris coverage percentages are 0%, 5%, 10% and 15%, respectively). The time of pedestrian needed to pass through the debris-covered area was recorded. The relationship between pedestrian velocity and the percentage of debris coverage were determined through data fitting. The pedestrian movement experiment will be introduced in detail in Section 4.

The influence of the percentage of debris coverage on the pedestrian velocity will be inputted to the pedestrian evacuation software Viswalk. Specifically, the lanes of roads that are covered by debris have smaller maximum pedestrian velocity than the lanes free from falling debris. Evacuation scenario is then established and pedestrian evacuation simulation can be conducted.

3 Prediction of falling debris distribution

Due to the lack of brick falling motion and distribution data, brick falling tests were firstly conducted, and the FE model of brick falling was established using LS-DYNA to simulate the motions of bricks. After the validation of the FE model using the brick falling test results, the FE model was further used to simulate the brick walls falling from different heights and with different initial velocities. Finally, the model to predict the distribution of debris was proposed by data regression.

3.1 Database of regional buildings and roads

With low density and outstanding soundproofing performance, aerated concrete blocks are widely used in the infilled walls of buildings. Therefore, this kind of bricks was selected to conduct the brick falling test. The size of the brick is 250 mm ¡Á 200 mm ¡Á 100 mm. Three heights (i.e. 1.8 m, 5.4 m and 9.0 m) were chosen, and the bricks were thrown with different horizontal initial velocities (Figure 3). The distance l and angle j of the final position of the brick on the ground are measured and recorded. Figure 4 illustrates the schematic diagram of brick falling tests.

Figure 3 Brick falling test

Figure 4 Schematic diagram of brick falling tests

To simulate the brick falling test in LS-DYNA, the material parameters of brick and the ground should be firstly determined. Among a number of material models in LS-DYNA that can be used for such simulation, the parameters of material model MAT 3 (LSTC, 2014) are the easiest to determine, and this model also shows a high computational stability in collision simulation. Therefore, MAT 3 was adopted to simulate the bricks and the ground. Material properties used in the simulation are listed in Table 1, which are measured through experiment. Contact algorithm Automatic-Node-To-Node (ANTN) (LSTC, 2014) is selected to model the interaction between the bricks and the ground.

Table 1 Material properties

Ten falling brick tests were performed and the results are listed in Table 2 and Figure 5, together with the FE simulation results. The comparison shows that the FE simulation agrees well with the test results, which validates the reliability of the FE model and parameters.

Table 2 Comparison of brick falling test results and FE simulation results

Figure 5 Comparison of brick falling tests and FE simulations

3.2 Debris distribution model

Debris may fall from different stories during an earthquake, and the final distribution of falling debris is related to the initial projectile velocity and the story where they come from. FE models were established to investigate the influence of various factors on debris distribution. Specifically, ten FE models of masonry infilled wall from the 1^st story to 10^th story were established in LS-DYNA (Figure 6(a)). The dimension of the infilled wall was determined by the story height of the building. Conventional story height of buildings is approximately 2.8-3.4 m (Hashemi & Mosalam, 2006; Pujol & Fick, 2010). Hence, the dimension of the FE model of the wall was 3.0 m in height and 4.0 m in width. The material parameters of the FE model were set according to the results of Section 3.1.

Figure 6 Debris simulation of masonry infilled wall in LS-DYNA

From the nonlinear time-history analysis of buildings in Module 2, the displacements and velocities of each story are then obtained. When the masonry infilled wall on a story exceeds the drift ratio limit, it will fail and the bricks of the masonry wall will undertake a horizontal projectile motion with the velocity of the story at that moment (Xu et al., 2016). The velocity of falling bricks can be divided into two orthogonal directions (i.e. X direction and Y direction). Simulation cases in LS-DYNA indicate that, debris distribution on the road is mainly influenced by velocity component in X direction, while velocity component in Y direction has limited impact. Consequently, only velocity component in X direction is considered in this work. According to existing studies (Lu et al., 2014; Xu et al., 2016), for buildings with conventional height, if the peak ground acceleration (PGA) is lower than 400 cm/s², the maximum velocity on different stories is lower than 2 m/s, basically. Therefore, four initial projectile velocities (i.e. 0.5 m/s, 1.0 m/s, 1.5 m/s and 2.0 m/s) were assigned to the wall. Consequently, 40 cases were simulated, and the debris distribution of each case was calculated (Figure 6(b)). The distribution of the falling debris can be predicted using Equation (1) from the regression of the FE results.

where P_d represents the percentage of target area (with a normalized width of 1.0 m) covered by debris; v_b represents the initial velocity (m/s); d represents the distance between the target area and the building (m); C₁ to C₅ are parameters, and each story has its own values, as listed in Table 3. Note that the debris of a target area may come from different stories. Therefore, the final percentage of debris coverage in the target area is the sum of the debris from each story.

Table 3 Parameter values of the debris distribution equation (Equation (1))

The comparison of FE results and the predictions of Equation (1) on the percentage of debris coverage is shown in Figure 7, which are in good agreement, thus validating the reliability and feasibility of Equation (1).

Figure 7 Comparison of FE results and the prediction of Equation (1) on the percentage of debris coverage

4 Pedestrian movement experiment

In the area covered by falling objects, the velocity of pedestrian will change, and roads may even be entirely blocked when the percentage of debris coverage is too large. To quantify the relationship between velocity and debris coverage percentage, pedestrian movement experiment in the scenario with debris is designed in this work.

The diameter of one person is approximately 0.7 m (Lakoba et al., 2005). Thus, a track with a width of 1.5 m and a length of 20 m was selected to implement the experiment. Four scenarios with different percentages of debris coverage were set (i.e. 0%, 5%, 10% and 15%), as shown in Figure 8(a) to 8(c). To avoid the injury when people are tripped by hard obstacles, paper boxes were chosen as obstacles, the size of which is 290 mm ¡Á 170 mm ¡Á 190 mm. In each scenario, every pedestrian passed through the track by walk as well as by run, and the walking and running time was recorded. There were 13 people taking part in the experiment. These participants are representatives of typical populations in the Chinese university community, whose age mostly ranges from 20 to 40 years old. Although the number of participants is not large, variations in age and gender are both taken into consideration. The experiment photos are shown Figure 9.

Figure 8 The track with different percentages of debris coverage

Figure 9 Pedestrian movement experiment

The pedestrian movement experiment found that when the percentage of debris coverage reaches 25% (Figure 8(d)), pedestrians can hardly pass through. Hence, the walk and run velocities are set to be 0 in this situation. The experimental results are shown in Figure 10, in which different points at the same percentage mean the results of different people. The regressions of the experimental results are shown in Equations (2) and (3), respectively.

where R represents reduction coefficient, v_p represents pedestrian velocity (m/s),  represents pedestrian velocity without debris (m/s), and P_d represents the percentage of debris coverage.

Figure 10 Fitting results of pedestrian velocity

5 Case study

The teaching region of Tsinghua University, consisting of 15 buildings and 1 playground, has a gross area of approximately 0.22 km². There are dense buildings and numerous people during the lecture time. Thus, this region is selected as the case study of pedestrian evacuation considering the falling debris. Playground is often used as emergency shelter site according to the design codes (MOHURD, 2007; CEA, 2008). Therefore, the playground in Figure 11 is set as the destination of the evacuation. Basic information of buildings is listed in Table 4. The total population involved in the case study is 6,230.

Table 4 Basic information of buildings

According to the Chinese Code for Seismic Design of Buildings (CMC, 2010), this region has a 8-degree seismic design intensity (the PGA is 200 cm/s² for a Design Basis Earthquake (DBE) with a return period of 475 years, and the PGA is 400 cm/s² for a Maximum Considered Earthquake (MCE) with a return period of 2475 years). A significant fault is located approximately 50 kilometers southeast of Tsinghua University (Wang et al., 2014). Therefore, the widely used far-field ground motion record, i.e., the El-Centro ground motion, is selected as a typical ground motion input, whose PGA is scaled to 400 cm/s². Both the north-south component and the east-west component are inputted to the buildings. Note that this PGA equals to the MCE level of the site. The buildings designed according to the code will not collapse, but severe damage will occur in the building, leading to the falling debris hazards.

Three evacuation scenarios are established herein:

Scenario 1: Pedestrian evacuation scenario with no debris;

Scenario 2: Pedestrian evacuation scenario with debris, in which the drift ratio limit of masonry infilled wall D_fall = 1/100;

Scenario 3: Pedestrian evacuation scenario with debris, in which the drift ratio limit of masonry infilled wall D_fall = 1/200.

Scenarios 2 and 3 are utilized to consider the uncertainty of drift ratio limit when infilled walls fail. The evacuation scenario is illustrated in Figure 11, where the blue polygons with inclined lines are buildings, the green areas are roads and the rectangle with grids is emergency shelter.

Figure 11 Schematic diagram of the evacuation area

Predicted debris distributions of the two scenarios with different drift ratio limits of the infilled wall are shown in Figure 12. Red polygons are blocked areas (i.e., the percentage of debris coverage is greater than 25%), where pedestrians can¡¯t pass through. Yellow polygons are reduced speed areas, which means the velocity of people will decrease due to falling debris when passing through. As the figures reveal, Road A with a width of 7 m (Figure 12) is completely blocked in both scenarios, which indicates that this road has extremely high risk of falling debris. Some people from Building #1, who will walk through this road in normal situation, have to choose another evacuation path. Note that if the motion of debris after hitting the ground is not considered, the first landing distance of the debris from the building envelop is less than 2.3 m. However, due to the collision and bounce of bricks on the ground (Figure 4(a)), the entire 7 m-width road is covered by debris. Therefore, the motion of bricks after hitting the ground should be taken into sufficient consideration.

Figure 12 Debris distribution

Compared to Scenario 3 in which the drift ratio limit D_fall = 1/200, in Scenario 2 (the drift ratio limit D_fall = 1/100) the blocked width of Road B decreases from 6 m to 3 m, while the blocked width of Road D decreases from 4 m to 2 m. Particularly, Road C is entirely blocked in Scenario 3, but people can pass through it in Scenario 2. Such different ranges of debris coverage mainly affect the people evacuating from Building #3. Moreover, the hazard ranges of falling debris in other areas of the two scenarios have little difference. But the percentages of debris coverage are different, thus affecting pedestrians¡¯ velocity.

Pedestrian evacuation subjected to these three scenarios was simulated, and each scenario was implemented three times. The influence of falling debris on the pedestrian velocity was considered using Equations (2) and (3). The evacuation time in these scenarios is shown in Table 5 and Figure 13. It costs 707 s for all people to reach the emergency shelter in Scenario 1 (i.e. without debris), which is approximately 10% shorter than that in Scenario 3 (i.e. with debris and D_fall = 1/200). When the drift ratio limit increases to D_fall = 1/100 (Scenario 2), the change of evacuation time is approximately 2%. In terms of the clearance time of 95% evacuees, the evacuation time of Scenario 3 is 15% longer than that of Scenario 1. The evacuation time of Scenario 2 and Scenario 3 is still close (the difference is less than 2%). Figure 13 also shows the same conclusion: the curve of Scenario 1 is significantly different from those of Scenarios 2 and 3, while the curves of Scenarios 2 and 3 are very close to each other. The results indicate that: the existence of debris will lead to a longer evacuation time, while different drift ratio limits have limited impact in this case study.

Table 5 Comparison of evacuation time in different scenarios

Figure 13 Comparison of different evacuation scenarios

Since the roads around Building #1 and Building #3 are affected by the falling debris seriously, the evacuation distances of people in these two buildings increase significantly (Figure 14). The average evacuation distance of people in Building #1 increases from 343 m in Scenario 1 (without debris) to 494 m in Scenario 2 (with debris), increased by approximately 44%. The evacuation time also increases significantly due to the longer evacuation distance and reduced evacuation velocity. Scenario 2 and Scenario 3 have almost the same evacuation distances. But the evacuation time of Scenario 3 is 5% longer than that of Scenario 2 due to the larger percentage of debris coverage as a result of a smaller drift ratio limits.

Figure 14 Comparison of evacuation results (Building #1 & Building #3)

By contrast, for the 360 pedestrians in Building #3, when compared to Scenario 1, the evacuation distance increases only 7% in Scenario 2, but evacuation time increases 25%. The reason for significantly longer evacuation time is that the debris reduces evacuation velocity. Consequently, the pedestrians will spend more time on the road. When comparing Scenario 2 and Scenario 3, the evacuation distance in Scenario 2 is 18% shorter than that in Scenario 3. However, the evacuation time of the former is only 6% less. The reason is that Road C is entirely blocked in Scenario 3 (Figure 12(b)), but there still exists a 1 m-width passage in Scenario 2 (Figure 12(a)), where people can still pass through. Thus, the evacuation distance in Scenario 2 is significantly shorter than that in Scenario 3. However, this passage is so narrow that congestions are prone to occur, thus seriously reducing the evacuation efficiency. Therefore, the difference of evacuation time is much less than that of evacuation distance.

The evacuation simulation results indicate that, although the total evacuation time due to different debris distributions doesn¡¯t change a lot, for the people in densely built-up areas, evacuation distance and time vary significantly, thus facing more risks during the evacuation. For some special roads, the variation of evacuation distance due to the change of debris distributions differs significantly with the variation of evacuation time. Therefore, it is necessary to accurately calculate the hazard ranges and percentage of debris coverage.

6 Conclusions

In this work, a framework for regional pedestrian evacuation simulation under the scenario with earthquake-induced falling debris is proposed. Hazard ranges of falling debris are predicted, and their influence on pedestrian movement is also quantified. A case study of the pedestrian evacuation simulation of the teaching area in Tsinghua University is performed. The following conclusions are obtained:

(1)    Based on brick falling tests and FE simulation, debris distribution models are proposed. Through pedestrian movement experiment, walking and running velocity models considering debris are proposed. Note that such models have never been reported in any existing studies.

(2)    The case study shows that whether the debris exists or not has more influence on the total evacuation time. Roads located in densely built-up areas have high risk of falling debris. Similarly, for people in these buildings, the existence of debris will significantly increase their evacuation distance and time.

(3)    When considering the motion after hitting the ground, hazard region of falling debris is much larger, which is essential to predict the debris distribution.

(4)    The methodology proposed herein is able to calculate the debris distribution during an earthquake, and the roads with high risk of falling debris can then be identified. Moreover, the influence of falling debris on pedestrian evacuation can also be quantified. This study is expected to provide a useful reference and technical support for post-earthquake emergency evacuation and urban planning.

Acknowledgement

The authors would like to acknowledge the financial supports of the National Key R&D Program (No. 2017YFC0702902) and the National Natural Science Foundation of China (No. U1709212).

References

American Society of Civil Engineers, 2010. Minimum design loads for buildings and other structures, ASCE 7-10. ASCE, Reston, VA.

Alexander, D.E., 1990. Behavior during earthquakes: a southern Italian example. International Journal of Mass Emergencies and Disasters 8, 5-29.

Belleri, A., Torquati, M., Marini, A., Riva, P., 2016. Horizontal cladding panels: in-plane seismic performance in precast concrete buildings. Bulletin of Earthquake Engineering 14, 1103-1129.

Bernardini, G., D¡¯Orazio, M., Quagliarini, E., 2016. Towards a ¡°behavioural design¡± approach for seismic risk reduction strategies of buildings and their environment. Safety Science 86, 273-294.

Chan, Y.F., Alagappan, K., Gandhi, A., Donovan, C., 2006. Disaster management following the Chi-Chi earthquake in Taiwan. Prehospital and Disaster Medicine 21, 196-202.

China Earthquake Administration, 2008. Emergency shelter for earthquake disasters¡ªsite and its facilities (GB 21734-2008). CEA, Beijing. (in Chinese)

China Ministry of Construction, 2010. Code for seismic design of buildings (GB50011-2010). CMC, Beijing. (in Chinese)

Cimellaro, G.P., Ozzello, F., Vallero, A., Mahin, S., Shao, B., 2017. Simulating earthquake evacuation using human behavior models. Earthquake Engineering & Structural Dynamics 46, 985-1002.

Dizhur, D., Ingham, J., Moon, L., Griffith, M., Schultz, A., Senaldi, I., Ventura, C., 2011. Performance of masonry buildings and churches in the 22 February 2011 Christchurch earthquake. Bulletin of the New Zealand Society for Earthquake Engineering 44, 279-296.

Dong, P.L., Guo, H.D., 2012. A framework for automated assessment of post-earthquake building damage using geospatial data. International Journal of Remote Sensing 33, 81-100.

D¡¯Orazio, M., Spalazzi, L., Quagliarini, E., Bernardini, G., 2014. Agent-based model for earthquake pedestrians¡¯ evacuation in urban outdoor scenarios: Behavioural patterns definition and evacuation paths choice. Safety Science 62, 450-465.

Duives, D.C., Daamen, W., Hoogendoorn, S.P., 2013. State-of-the-art crowd motion simulation models. Transportation Research Part C: Emerging Technologies 37, 193-209.

Federal Emergency Management Agency, 2012. Seismic performance assessment of buildings volume 1¨Cmethodology (FEMA-P58). FEMA, Washington, DC.

Goretti, A., Sarli, V., 2006. Road network and damaged buildings in urban areas: short and long-term interaction. Bulletin of Earthquake Engineering 4, 159-175.

Haklay, M., Patrick, W., 2008. Openstreetmap: user-generated street maps. IEEE Pervasive Computing 7, 12-18.

Hashemi, A., Mosalam, K.M., 2006. Shake-table experiment on reinforced concrete structure containing masonry infill wall. Earthquake Engineering & Structural Dynamics 35, 1827-1852.

Helbing, D., Molnar, P., 1995. Social force model for pedestrian dynamics. Physical Review E 51, 4282-4286.

Henningsson, J., Blomstrand, J., 2015. Verification and validation of Viswalk for building evacuation modelling. Lund University, Sweden.

Hirokawa, N., Osaragi, T., 2016. Earthquake disaster simulation system: integration of models for building collapse, road blockage, and fire spread. Journal of Disaster Research 11, 175-187.

Johansson, A., Helbing, D., Al-Abideen, H.Z., Al-Bosta, S., 2008. From crowd dynamics to crowd safety: a video-based analysis. Advances in Complex Systems 11, 497-527.

Karimzadeh, S., Miyajima, M., Hassanzadeh, R., Amiraslanzadeh, R., Kamel, B., 2014. A GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil Dynamics and Earthquake Engineering 66, 263-280.

Kaushik, H.B., Rai, D.C., Jain, S.K., 2006. Code approaches to seismic design of masonry-infilled reinforced concrete frames: a state-of-the-art review. Earthquake Spectra 22, 961-983.

Lakoba, T.I., Kaup, D.J., Finkelstein, N.M., 2005. Modifications of the Helbing-Molnar-Farkas-Vicsek social force model for pedestrian evolution. Simulation 81, 339-352.

Lee, T.H., Kato, M., Matsumiya, T., Suita, K., Nakashima, M., 2007. Seismic performance evaluation of non-structural components: drywall partitions. Earthquake Engineering & Structural Dynamics 36, 367-382.

Li, M., Zhao, Y., He, L., Chen, W., Xu, X., 2015. The parameter calibration and optimization of social force model for the real-life 2013 Ya¡¯an earthquake evacuation in China. Safety Science 79, 243-253.

Li, Y., Lu, X.Z., Guan, H., Ye, L.P., 2014. Progressive collapse resistance demand of RC frames under catenary mechanism. ACI Structural Journal 111, 1225-1234.

Liu, Z., Jacques, C.C., Szyniszewski, S., Guest, J.K., Schafer, B.W., Igusa, T., Mitrani-Reiser, J., 2015. Agent-based simulation of building evacuation after an earthquake: coupling human behavior with structural response. Natural Hazards Review 17, 4015019.

Livermore Software Technology Corporation, 2014. LS-DYNA keyword user¡¯s manual volume II material models, LS-DYNA R7.1. LSTC, Livermore, CA.

Lu, X., Lu, X.Z., Guan, H., Ye, L.P., 2013. Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes. Earthquake Engineering & Structural Dynamics 42, 705-723.

Lu, X.Z., Han, B., Hori, M., Xiong, C., Xu, Z., 2014. A coarse-grained parallel approach for seismic damage simulations of urban areas based on refined models and GPU/CPU cooperative computing. Advances in Engineering Software 70, 90-103.

Ministry of Housing and Urban-Rural development of the People¡¯s Republic of China, 2007. Standard for urban planning on earthquake resistance and hazardous prevention (GB 50413-2007). MOHURD, Beijing. (in Chinese)

Miranda, E., Mosqueda, G., Retamales, R., Pekcan, G., 2012. Performance of nonstructural components during the 27 February 2010 Chile Earthquake. Earthquake Spectra 28, 453-471.

Mousavi, S., Bagchi, A., Kodur, V.K.R., 2008. Review of post-earthquake fire hazard to building structures. Canadian Journal of Civil Engineering 35, 689-698.

Osaragi, T., Morisawa, T., Oki, T., 2014. Simulation model of evacuation behavior following a large-scale earthquake that takes into account various attributes of residents and transient occupants. Pedestrian and Evacuation Dynamics 2012, pp. 469-484. Springer, Cham.

Parisi, D.R., Gilman, M., Moldovan, H., 2009. A modification of the Social Force Model can reproduce experimental data of pedestrian flows in normal conditions. Physica A: Statistical Mechanics and Its Applications 388, 3600-3608.

Peek-Asa, C., Kraus, J.F., Bourque, L.B., Vimalachandra, D., Yu, J., Abrams, J., 1998. Fatal and hospitalized injuries resulting from the 1994 Northridge earthquake. International Journal of Epidemiology 27, 459-465.

PTV Group, 2016. VISSIM 9-User Manual. PTV, Karlsruhe, Germany.

Pujol, S., Fick, D., 2010. The test of a full-scale three-story RC structure with masonry infill walls. Engineering Structures 32, 3112-3121.

Qiu, J., Liu, G.D., Wang, S.X., Zhang, X.Z., Zhang, L., Li, Y., Yuan, D.F., Yang, Z.H., Zhou, J.H., 2010. Analysis of injuries and treatment of 3401 inpatients in 2008 Wenchuan earthquake¡ªbased on Chinese Trauma Databank. Chinese Journal of Traumatology 13, 297-303.

Quagliarini, E., Bernardini, G., Wazinski, C., Spalazzi, L., D¡¯Orazio, M., 2016. Urban scenarios modifications due to the earthquake: ruins formation criteria and interactions with pedestrians¡¯ evacuation. Bulletin of Earthquake Engineering 14, 1071-1101.

Restrepo, J.I., Bersofsky, A.M., 2011. Performance characteristics of light gage steel stud partition walls. Thin-Walled Structures 49, 317-324.

Saito, K., Spence, R., Going, C., Markus, M., 2004. Using high-resolution satellite images for post-earthquake building damage assessment: a study following the 26 January 2001 Gujarat Earthquake. Earthquake Spectra 20, 145-169.

UN-Habitat, 2016. World Cities Report 2016. UN-Habitat, Nairobi, Kenya.

Wan, J., Sui, J., Yu, H., 2014. Research on evacuation in the subway station in China based on the Combined Social Force Model. Physica A: Statistical Mechanics and Its Applications 394, 33-46.

Wang, X.S., Feng, X.D., Xu, X.W., Diao, G.L., Wan, Y.G., Wang, L.B., Ma, G.Q., 2014. Fault plane parameters of Sanhe-Pinggu M8 earthquake in 1679 determined using present-day small earthquakes. Earthquake Science 27, 607-614.

Wijerathne, M.L.L., Melgar, L.A., Hori, M., Ichimura, T., Tanaka, S., 2013. HPC enhanced large urban area evacuation simulations with vision based autonomously navigating multi agents. Procedia Computer Science 18, 1515-1524.

Wu, Y.J., Wang, Y., Qian, D., 2007. A google-map-based arterial traffic information system. Intelligent Transportation Systems Conference 2007, IEEE, 968-973. Bellevue, WA.

Xiao, M.L., Chen, Y., Yan, M.J., Ye, L.Y., Liu, B.Y., 2016. Simulation of household evacuation in the 2014 Ludian earthquake. Bulletin of Earthquake Engineering 14, 1757-1769.

Xiong, C., Lu, X.Z., Guan, H., Xu, Z., 2016. A nonlinear computational model for regional seismic simulation of tall buildings. Bulletin of Earthquake Engineering 14, 1047-1069.

Xiong, C., Lu, X.Z., Hori, M., Guan, H., Xu, Z., 2015. Building seismic response and visualization using 3D urban polygonal modeling. Automation in Construction 55, 25-34.

Xiong, C., Lu, X.Z., Lin, X.C., Xu, Z., Ye, L.P., 2017. Parameter determination and damage assessment for THA-based regional seismic damage prediction of multi-story buildings. Journal of Earthquake Engineering 21, 461-485.

Xu, Z., Lu, X.Z., Guan, H., Tian, Y., Ren, A.Z., 2016. Simulation of earthquake-induced hazards of falling exterior non-structural components and its application to emergency shelter design. Natural Hazards 80, 935-950.

Yamazaki, F., Yano, Y., Matsuoka, M., 2005. Visual damage interpretation of buildings in bam city using quickbird images following the 2003 bam, Iran, earthquake. Earthquake Spectra 21, 329-336.

Yang, Z.H., Lan, H.X., Gao, X., Li, L.P., Meng, Y.S., Wu, Y.M., 2015. Urgent landslide susceptibility assessment in the 2013 Lushan earthquake-impacted area, Sichuan Province, China. Natural Hazards 75, 2467-2487.

Zeng, X., Lu, X.Z., Yang, T.Y., Xu, Z., 2016. Application of the FEMA-P58 methodology for regional earthquake loss prediction. Natural Hazards 83, 177-192.

Zhao, B., Taucer, F., Rossetto, T., 2009. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China. Engineering Structures 31, 1707-1723.