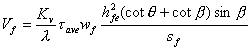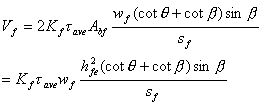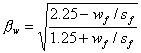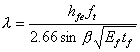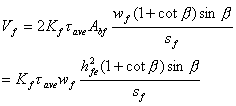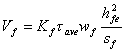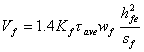FRP-混凝土界面行为研究/Studies on FRP-Concrete Interface
陆新征/Xin-zheng Lu
清华大学工学博士学位论文 / Tsinghua University Dissertation
2004
第九章 抗剪加固剥离的分析
9.1 引言
上一章回顾了外贴FRP用于钢筋混凝土梁的抗剪加固方法、试验研究和受剪剥离承载力计算公式。可以看出，当前对受剪剥离的破坏机理虽有一定认识，但还不是很清楚，有关计算公式或是依据主要影响参数进行回归，或是利用面内剪切剥离承载力计算公式，因此从受剪剥离机理上来说都存在一定的问题。而本文第五章提出的FRP-混凝土界面粘结-滑移本构模型，则为抗剪加固剥离分析和全面了解受剪剥离机理提供了基础。基于前文成果，本章进行了以下研究工作：
(1) 进行了5个抗剪加固剥离试验研究，了解受剪剥离破坏的基本过程，量测了剥离破坏的承载力和FRP应变分布；
(2) 建立了FRP抗剪加固的有限元模型，根据有限元分析结果，说明第五章提出的粘结-滑移关系可以用于分析受剪剥离问题，并根据有限元模型讨论了受剪剥离破坏的过程；
(3) 对受剪斜裂缝宽度分布规律进行了讨论，提出了3种典型斜裂缝形状，由此建立了沿斜裂缝FRP滑移分布模型；
(4) 以FRP滑移分布模型为基础，分析了达到受剪剥离破坏时FRP的应力分布，讨论了粘结长度和粘贴方式的影响，得到了FRP抗剪贡献与粘结长度、粘贴方式等参数之间的关系；
(5) 基于上述讨论，提出抗剪加固剥离承载力设计公式。
9.2 试验研究
9.2.1 试验方案
试验梁截面尺寸为150mm×260mm，长度为1500mm。为保证梁在数据量测区一侧破坏，在非数据量测区配置了较多的箍筋，典型试件配筋见图9-1。通过变化FRP条带宽度wf和条带净距离sf来研究FRP的加固量影响，其它研究参数还有剪跨比、FRP类型等。各试验梁的参数、FRP加固形式，以及加载和量测方案如表9-1及图9-2和图9-3。箍筋和FRP材料的力学性能见表9-2。GFRP和CFRP的厚度分别为0.169mm和0.111mm。试验中主要量测荷载及梁跨中挠度，箍筋应变，斜裂缝附近FRP的应变。
图9-1 典型试件配筋图
图9-2 FRP加固形式
图9-3 试验加载及FRP应变片布置图
表9-1 试验梁参数及加固方案
|
试件编号 |
剪跨比 |
fcu |
加固形式 |
箍筋 |
wf |
sf |
|
S-GU-1-1 |
1.50 |
39.2 |
U(GFRP) |
f6-200 |
50 |
50 |
|
S0-2-0 |
2.16 |
31.8 |
无 |
― |
－ |
|
|
S-GU-2-1a |
39.2 |
U(GFRP) |
50 |
50 |
||
|
S-GU-2-3 |
38.3 |
U(GFRP) |
500 |
0 |
||
|
S-CU-2-1 |
37.6 |
U(CFRP) |
50 |
50 |
||
|
S-GU-3-1 |
2.80 |
40.1 |
U(GFRP) |
f6-200 |
50 |
50 |
表9-2 钢筋及FRP材料性能（MPa）
|
箍筋 |
FRP布 |
||||
|
类型 |
屈服强度(MPa) |
极限强度(MPa) |
类型 |
抗拉强度(MPa) |
弹性模量(GPa) |
|
f6钢筋 |
377 |
555 |
GFRP |
2802 |
102.1 |
|
f8钢筋 |
307 |
435 |
CFRP |
3500 |
235.0 |
9.2.2 试验结果
表9-3列出了各试验梁的开裂荷载Vcr、FRP起始剥离荷载Vd和最大荷载Vu，以及消除混凝土强度影响后无量纲化的最大荷载相对于S0-2-0（未加固对比梁）的提高程度。U型FRP加固梁的受剪剥离过程为：斜裂缝出现后，斜裂缝穿过处的U型FRP箍附近首先产生微小的剥离。随着荷载增大，剥离范围从斜裂缝处分别向上下发展，直至发展到梁顶和梁底。典型的FRP剥离破坏形态如图9-4所示。
表9-3 试验梁特征点荷载(kN)
|
试件编号 |
(kN) |
(kN) |
(kN) |
|
|
|
承载力 提高(%) |
|
S-GU-1-1 |
48.8 |
112.3 |
173.4 |
0.476 |
1.095 |
1.692 |
―― |
|
S0-2-0 |
40.0 |
0 |
102.6 |
0.438 |
0.000 |
1.123 |
―― |
|
S-GU-2-1a |
34.3 |
149 |
150.4 |
0.335 |
1.453 |
1.467 |
30.6 |
|
S-GU-2-3 |
45.6 |
169.6 |
171.6 |
0.451 |
1.677 |
1.696 |
51.0 |
|
S-CU-2-1 |
40.1 |
134.7 |
146.9 |
0.401 |
1.345 |
1.389 |
23.6 |
|
S-GU-3-1 |
40.4 |
109.7 |
109.9 |
0.389 |
1.057 |
1.059 |
―― |
试验得到的FRP应变分布发展规律如图9-5所示。在箍筋屈服前，FRP应变不大，在箍筋屈服后，FRP应变迅速增加，基本规律是在斜裂缝中部最大，顶部和底部最小。
(a) S-GU-2-1a梁GFRP剥离破坏 (b) S-CU-2-1梁CFRP剥离和拉断破坏
注：剥离顺序为U2、U3和U4 U1、U2、U3几乎同时剥离，而后U4箍拉断
图9-4 试验梁的破坏照片
(a) S-GU-2-1a (b) S-CU-2-1
图9-5 试验FRP应变分布发展
9.3 有限元分析
9.3.1 有限元模型
抗剪承载力计算一直是钢筋混凝土有限元分析的一个难点。尽管之前很多研究者做了大量的探索性工作 [15] ，但是目前还没有一个能够圆满解决受剪计算问题的模型。因为本章的工作重点是研究FRP加固对抗剪承载力的贡献，如何建立一个更好的钢筋混凝土抗剪计算模型并不是本章要研究的重点，因此本章采用最常用的钢筋混凝土梁抗剪有限元分析方法，即：
(1) 计算软件依然基于通用有限元软件MSC.MARC [73] ；
(2) 钢筋和混凝土单元同7.5节，FRP采用平面单元(Element 3 in MSC.MARC)，FRP和混凝土之间的界面用弹簧单元(Spring element in MSC.MARC)，弹簧的荷载位移关系采用第五章建议的粘结-滑移本构关系；
(3) 钢筋、混凝土、FRP材料模型同7.5节，其中，混凝土的剪力传递系数采用Al-Mahaidi
[77] 建议的变剪力传递系数模型加以模拟（式4.6d）。由于钢筋混凝土抗剪承载力对剪力传递系数非常敏感，因此式(4.6d)中的 
作为待定参数，根据试验结果推算。
需要说明的是，由于受剪斜裂缝一般比较集中，因此其剥离破坏过程相对与受弯剥离而言比较简单，与面内剪切剥离过程更加相近。因此，在这里就没有引入受弯剥离使用的双剥离破坏准则，而是直接根据FRP和混凝土节点的相对位移来判断是否达到剥离破坏，即如果FRP节点和混凝土节点之间的滑移量大于剥离滑移，则认为发生剥离破坏。
9.3.2 计算结果
以9.2节的未加固试件S-0-2-0为基准，取 
从40~200με以20με为间隔逐个试算，结果发现当 
时，计算结果和试验结果吻合最好。
用上述 
计算9.2节的其他FRP加固试件，得到的抗剪承载力和试验值对比如表9-4所示。可见有限元分析承载力结果和试验值吻合良好，说明第五章所建议的粘结-滑移模型用于分析受剪剥离也是可行的。
以试件S-GU-2-1a（U型加固）为例，计算得到的斜裂缝发展与试验对比如图9-6所示，可见斜裂缝宽度(云图颜色越深表示开裂应变越大，裂缝越宽)基本是在顶部为零，中部附近最大，而后向底部又逐渐变小。
表9-4 计算承载力和试验值对比
|
试件名称 |
计算值(kN) |
试验值(kN) |
误差 |
|
S0-2-0 |
205.2 |
194.3 |
5.61% |
|
S-GU-2-1a |
271.5 |
294.1 |
-7.68% |
|
S-GU-2-3 |
333.7 |
336.2 |
-0.74% |
|
S-GU-1-1 |
349.4 |
339.9 |
2.79% |
|
S-GU-3-1 |
249.3 |
215.4 |
15.7% |
|
S-CU-2-1 |
276.0 |
272.6 |
1.25% |
(a) 开始剥离时
(b) 最大荷载
图9-6 有限元与试验裂缝分布对比
计算得到的FRP应力分布和试验对比如图9-7所示。需要说明的是，由于试验应变片未必正好贴在斜裂缝上，因此在图9-7中将有限元分析得到的应变片位置FRP应力以及斜裂缝上的FRP应力分布分别绘制出来。从图中可以看出，计算结果和试验结果是比较吻合的，而斜裂缝上的FRP应力分布表现出更加复杂的行为，主要是在斜裂缝穿过箍筋和纵筋的位置，因斜裂缝开展受到约束而减小，故FRP的应力也小一些。
图 9-7 FRP应力分布对比
根据图9-6和9-7的结果可以看出，由于斜裂缝宽度的影响，FRP的应力在斜裂缝顶部最小，而后向中部逐渐增加，在底部附近由于纵筋和U型箍的约束作用使斜裂缝宽度又有所降低，使得FRP的应力变小。需要说明的是，现在大部分抗剪加固试件，包括9.2节的试件，为保证试验最终为受剪破坏，一般底部的纵筋都布置得比较多，故对底部斜裂缝发展的约束作用也比较强，使斜裂缝底部的宽度一般都比较小。而实际工程构件则未必如此，在受剪破坏时，斜裂缝底部的宽度也可能比较大。另外，另一些试验发现 [37] 受剪加固量比较大或梁高较大时，出现的斜裂缝可能不止一条，其受剪剥离破坏的机理也更加复杂。
计算得到的剥离破坏过程和试验得到的剥离破坏过程对比如图9-8所示。其中，试验剥离破坏从图中表现为FRP泛白或剥落，计算剥离破坏从图中表现为FRP单元边界和混凝土单元边界位置有较大差异。从对比中可以看出，无论是计算还是试验都发现，由于斜裂缝总是在梁中部最大，所以剥离首先都是从梁中部开始(图9-8a)；但是，由于中部的粘结长度比较长，剥离破坏有个发展过程，所以受剪承载力可以继续维持并升高。随着斜裂缝宽度的进一步加大，斜裂缝顶部的FRP开始发生剥离。由于斜裂缝顶部的FRP粘结长度很短，所以很快就退出工作(图9-8b)，这时承载力也达到最大值。而后斜裂缝继续发展，底部和中部的FRP最终完全从混凝土表面剥离下来，退出工作(图9-8c)。
从有限元分析和试验结果中可以看出，FRP应力分布不是像Chen & Teng公式 [157] 所假设的那样同时达到各自的剥离承载力，而是随着斜裂缝宽度的发展而有一个逐步发展的过程。FRP的最大抗剪贡献不但和粘贴长度有关，也和斜裂缝的宽度分布有关，因此讨论FRP应力分布问题，首先要对斜裂缝宽度分布进行研究。
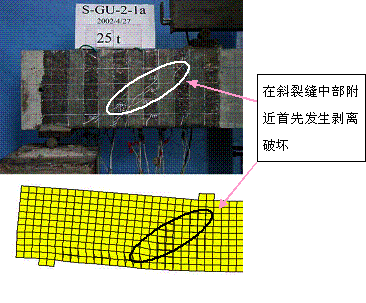
(a) 开始出现剥离
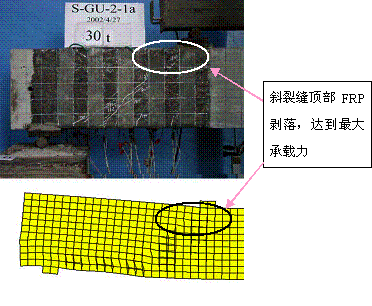
(b) 顶部FRP剥离退出工作
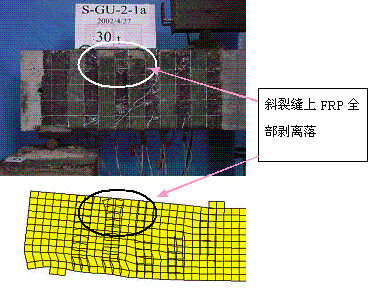
(c) 斜裂缝上所有FRP 都退出工作
图9-8 计算和试验剥离破坏过程对比
9.4 FRP应力分布规律
9.4.1 斜裂缝形状的简化
有限元分析为了解FRP应力分布规律提供了很好的依据。从有限元模型中可以看出，受剪剥离破坏过程和斜裂缝宽度分布关系密切。但是，由于有限元模型本身牵涉到的因素比较多，且钢筋混凝土受剪破坏有限元分析本身的难度也比较大，完全依赖有限元分析研究FRP加固的抗剪剥离破坏机理有一定的难度。因此，为了建立受剪加固的简化计算模型，本节根据试验研究和有限元分析的结果，对斜裂缝宽度分布规律进行适当的简化，并根据简化的斜裂缝模型和FRP-混凝土的粘结-滑移关系来研究FRP的应力分布规律。
由于混凝土梁顶部肯定是受压的，因此斜裂缝顶部宽度势必为零。斜裂缝在梁底部的宽度受纵筋配筋率影响而各有不同，因此本文提出以下3种简化的斜裂缝宽度分布模型，如图9-9所示，其中菱形分布的斜裂缝底部宽度为零，锥形分布斜裂缝宽度从中部到底部相同，而线性分布斜裂缝宽度从顶部到底部线性增大。这三种简化模型代表了三个不同的典型斜裂缝形状，而真实的受剪破坏斜裂缝形状介于这三者之间。
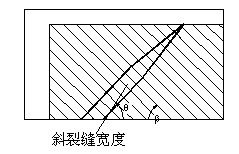
(a) 菱形分布 (b) 锥形分布
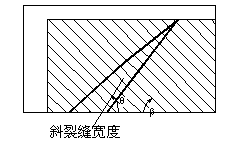
(c) 线性分布
图 9-9 斜裂缝简化模型
9.4.2 滑移场模型
当斜裂缝宽度变化规律确定下来以后，如果假设斜裂缝两侧FRP的滑移量相等，则裂缝两侧FRP的滑移分布就与裂缝宽度分布规律相同，分别称菱形斜裂缝、锥形斜裂缝、线性斜裂缝对应的滑移场分布为双线性滑移场，梯形滑移场和线性滑移场，如图9-10所示。另外，还考虑了均匀滑移场的情况，相当于斜裂缝宽度不变，如图9-10d所示。一般说来，均匀滑移场只有在粘贴长度很短的时候才会出现，工程中一般不会遇到，只是作为一个特殊情况加以讨论。
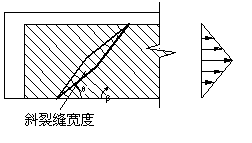
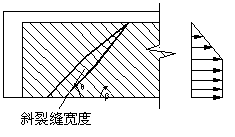
(a) 双线性滑移场 (b) 梯形滑移场
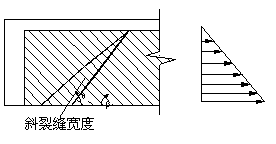
(c) 线性滑移场 (d) 均匀滑移场
图9-10 滑移场模型
9.4.3 计算模型
将与斜裂缝相交的FRP取出，建立如图9-11所示的隔离体（图中阴影区）。如果是U型粘贴，则斜裂缝以上的FRP都会剥离，如图9-11a所示；如果是侧面粘贴则FRP，则既可能从顶部剥离，也可能从底部剥离，如图9-11b所示。将剥离下来的FRP与上一节提到的4种不同的滑移场模型组合，可以得到相应的计算模型如图9-12及表9-5所示。
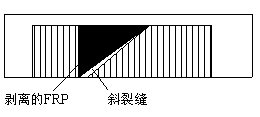
(a) U型粘贴 (b) 侧面粘贴
图 9-11 不同加固方式剥离的FRP面积
表 9-5 FRP隔离体模型
|
计算模型名称 |
粘贴方式 |
滑移场模型 |
|
模型A |
U型 |
双线性滑移场 |
|
模型B |
梯形滑移场 |
|
|
模型C |
线性滑移场 |
|
|
模型D |
均匀滑移场 |
|
|
模型E |
侧面 |
双线性滑移场 |
|
模型F |
梯形滑移场 |
|
|
模型G |
线性滑移场 |
|
|
模型H |
均匀滑移场 |
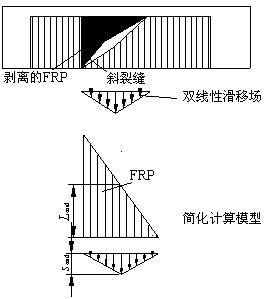
(a) 模型A (b) 模型B
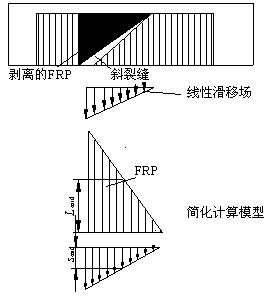
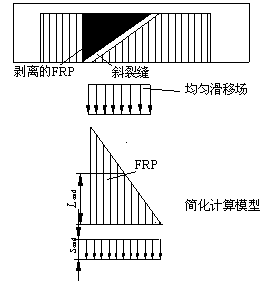
(c) 模型C (d) 模型D
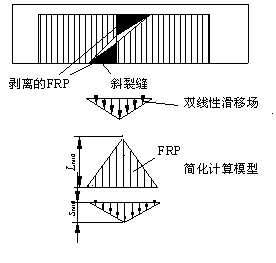
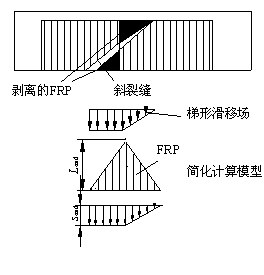
(e) 模型E (f) 模型F
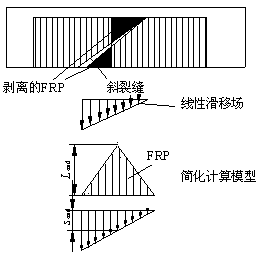
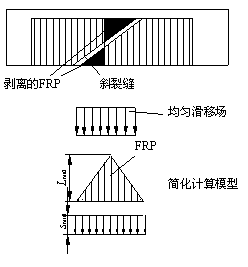
(g) 模型G (h) 模型H
图 9-12 各种受剪剥离的计算模型
将上述计算模型中的FRP简化为一根根由链杆单元组成的纤维，每个链杆单元的节点通过弹簧单元固定在混凝土上，如图9-13所示。弹簧的本构关系服从第五章提出的粘结-滑移关系。在FRP端部按滑移场逐级施加位移，就可以得到各个模型中FRP的应力分布、以及平均应力和滑移之间的关系。当然，实际FRP未必和斜裂缝正好垂直，但后面通过角度变换可以考虑斜交的影响。
令中间FRP纤维的长度为Lmid，各模型的Lmid见图9-12。定义，
|
|
(9.1) |
式中，Le为FRP的有效锚固长度，按式(5.5e)计算。根据分析结果，可以得到不同
下FRP平均应力和中部滑移量smid之间的关系。
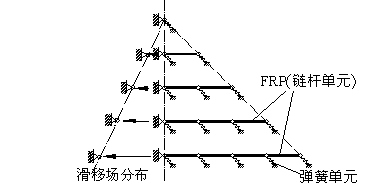
图 9-13 FRP受剪剥离的计算模型
9.4.4 计算结果
以模型A（图9-12a，双线性滑移场，U型粘贴） 
的情况为例，按上述模型分析得到的FRP的相对平均应力与相对滑移量的典型关系如图9-14所示(混凝土强度ft=3MPa，FRP轴向刚度为Eftf=16GPa·mm)，图中，s0为粘结-滑移本构中达到峰值粘结应力对应的滑移量，由式(5.1c)给出； 
为FRP平均应力； 
为锚固长度无限长的情况下，FRP的最大剥离应力，根据第五章式(5.5)可得：
|
|
(9.2) |
图9-14 滑移量和平均应力的关系
从图9-14可见，当smid/s0达到6.29时（对于ft=3MPa时，相当于最大斜裂缝宽度达到大约0.7mm），FRP的平均应力达到最大值，而后随着smid继续增大，越来越多的FRP由于剥离退出工作，使得整个FRP的平均应力降低。
模型A 
时FRP应力分布随滑移增加的变化关系如图9-15所示。由图可见，在滑移量（即斜裂缝张开量）较小时（ 
），FRP应力分布形状与滑移场相近；随着裂缝张开程度的增大，粘结-滑移关系非线性日益明显，相应顶部附近FRP由于锚固长度短，非线性行为更加明显，应力也相对较低（ 
）；当裂缝中部滑移 
时，整个裂缝断面上FRP的总荷载达到最大值；之后，顶部附近FRP进入荷载滑移关系的软化段，该处的FRP应力降低，整个裂缝断面上FRP的平均应力也随之下降（
）。
图 9-15 斜裂缝上FRP应力分布
如果将图9-15的FRP应力分布发展过程和图9-8有限元及试验得到的剥离破坏过程相对照，可以看出，对于S-GU-2-1a试件，其裂缝形状接近于菱形分布（图9-7），其剥离破坏过程也和模型A的预测结果完全一致，即：首先在斜裂缝中部（斜裂缝宽度最大处）的FRP达到剥离承载力，而后斜裂缝宽度继续变大，斜裂缝顶部FRP由于锚固长度短而先退出工作，这时FRP的抗剪贡献达到最大值。
对于模型A，在不同 
情况下，FRP平均应力达到最大（称为峰值FRP平均应力 
）时FRP的应力分布（称为峰值FRP应力分布）如图9-16所示。不同混凝土强度和FRP刚度的模型计算得到的FRP应力分布结果差别很小，故不再讨论其影响。从图中可以看出，随
增大，即相对粘结长度增加，FRP应变分布逐渐趋向均匀，但FRP应力的最大值 
却未必一定在斜裂缝宽度最大的中间位置，而是根据滑移场和FRP粘贴方式不同而有所变化。当 
时，最大FRP应力 
可以达到 
。
图 9-16 不同 
对应的峰值FRP应力分布（模型A）
对于模型C（图9-12c，线性滑移场，U型粘贴），情况则有所不同，模型C在不同 
情况下的峰值FRP应力分布如图9-17所示。从图中可以看出，当
时，即最大粘结长度（位于斜裂缝底部）小于有效锚固长度时，峰值FRP应力分布基本和滑移场形状相似，在斜裂缝顶部最小，底部最大，但是最大FRP应力 
；当 
时，最大粘结长度（位于斜裂缝底部）超过有效锚固长度，此时 
可以达到 
，且分布随 
增大而逐步趋于均匀。
图 9-17 不同 
对应的峰值FRP应力分布（模型C）
由图9-15、9-16和9-17可知，FRP应力分布和斜裂缝形状关系密切。对于U型粘贴加固，如果斜裂缝宽度分布为线性分布，则最大的FRP应力 
出现在最大粘结长度处（斜裂缝底部），这与Chen & Teng模型假设情况一致。但是，如果裂缝宽度为菱形分布，则 
出现在梁中部附近，这与Chen & Teng模型的假设情况完全不同。
令
|
|
(9.3) |
由数值计算得到不同模型的
与 
的关系如图9-18所示。另外，根据Chen & Teng
[157] 的模型，可以得到在该模型中的
表达式为：
|
|
(9.4) |
如 
和 
均按Chen & Teng公式取值，其结果也绘于图9-18中。
(a) U型加固计算模型（模型A~D） 
~ 
关系
(b) 侧面粘贴加固计算模型（模型E~H） 
~ 
关系
图9-18 不同模型 
~ 
关系比较
如前所述，由于混凝土中实际斜裂缝的宽度分布规律非常复杂，用前述任何一个简单的简化斜裂缝模型来描述斜裂缝分布都是不全面的。但是，实际混凝土的斜裂缝形状必然介于前述3种典型斜裂缝之间。出于工程设计保证安全的目的，本文选择最不利的斜裂缝宽度分布模型来建立FRP的受剪剥离承载力设计公式。从图9-18a中可以看出，模型A，即斜裂缝宽度为菱形时，是3种裂缝模型中最不利的。虽然模型D（即均匀斜裂缝宽度分布）在
时的 
要小于模型A，但是因为实际U型加固在梁底存在较强的约束，且模型D只有在粘结长度很小时才可能出现，因此这种可能性较小，可以不予考虑。同样的，对于侧面粘贴情况，可以看出模型G，即斜裂缝宽度分布为线性张开时，是最不利情况。因此，本文分别基于模型A和模型G来建立FRP的受剪剥离承载力设计公式。
如果将不同模型的FRP应变不均匀系数
加以对比，如图9-19所示。对于U型粘贴，不同模型
的差距并不显著；但是对于侧面粘贴，不同模型的 
差距较大。Chen & Teng模型假设所有FRP都能同时达到其剥离承载力，由此得到的 
可能是偏于不安全的。
(a) U型粘贴
(b) 侧面粘贴
图 9-19 不同模型加固 
~ 
关系
9.5 设计公式
在确定了最不利的受剪剥离模型后，就可以根据该模型得到的
~ 
关系提出相应的设计公式。之所以选择 
~ 
关系，是因为所有与相对粘结长度 
有关的影响，都可以通过 
加以反映。而Chen & Teng建议的方法中，则同时有两个变量，即 
和 
都是和 
有关，且参数回归非常麻烦。
对于U型加固，根据模型A计算得到的 
~ 
关系进行拟合，用下式可以较好地拟合该曲线，
|
|
(9.5a) |
拟合结果与数值结果对比如图9-20所示，可见二者吻合良好。
图9-20 U型粘贴 
~ 
关系拟合
同样，对于侧面粘贴，模型G为最不利情况。对模型G的
~l关系进行拟合得到，
|
|
(9.5b) |
拟合结果和数值结果对比如图9-21所示，可见二者吻合良好。
图9-21侧面粘贴 
~ 
关系拟合
同时，考虑FRP纤维粘贴的角度 
的影响，则 
的计算公式可以修改为：
|
|
(9.6) |
式中， 
的含义同图8-5。
综合本节上述讨论，本文建议的FRP的受剪剥离承载力计算公式如下：
|
|
(9.7a) |
|
|
|
(9.7b) |
对U型箍加固情况，
|
|
(9.7c) |
对侧面粘贴加固情况，
|
|
(9.7d) |
|
|
|
(9.7e) |
|
|
|
(9.7f) |
|
|
|
(9.7g) |
|
|
|
(9.7h) |
该式预测结果和试验结果对比如图9-22和表9-6，9-7所示，可见该公式计算结果和试验结果吻合良好，其精度和Chen & Teng模型不相上下。需要说明的是，目前本文所收集到的受剪加固试验资料一般都布置了大量的纵筋以防止受弯破坏，因此模型A假设的情况和试验结果比较吻合，但对于一般工程构件，如果纵筋数量有限的话，可能会出现模型B或C的情况，但是由于模型A比这两个模型都偏于保守，因此作为设计公式也是完全恰当的。而Chen & Teng模型此时可能偏于不安全。
(a) U型粘贴加固 (b) 侧面粘贴加固
图 9-22 式(9.7)
与试验值比较
表9-6 
计算值与试验值对比(U型加固)
|
计算值/试验值 |
变异系数 |
相关系数 |
||||
|
A组 |
B组 |
A组 |
B组 |
A组 |
B组 |
|
|
式(9.7) |
0.89 |
0.95 |
0.26 |
0.22 |
0.76 |
0.76 |
|
式(9.11) |
0.81 |
0.86 |
0.25 |
0.23 |
0.77 |
0.75 |
|
式(9.12) |
0.64 |
0.65 |
0.29 |
0.31 |
0.41 |
0.31 |
表9-7 
计算值与试验值对比(侧面粘贴加固)
|
计算值/试验值 |
变异系数 |
相关系数 |
|
|
式(9.7) |
0.99 |
0.29 |
0.76 |
|
式(9.11) |
0.93 |
0.30 |
0.76 |
|
式(9.12) |
0.69 |
0.46 |
0.43 |
本文建议模型和试验得到的剥离承载力时FRP应力对比如图9-23所示。从图中可以看出，本文建议的模型比Chen & Teng的模型更加接近于试验的FRP应力分布。这和9.3节讨论的裂缝宽度分布规律是一致的。尽管本文建议模型预测的FRP应力分布和试验实测应力分布还有一些差异，但是相比起现有模型而言，该应力分布模型已经改进了很多。
(a) S-GU2-1a (b) S-GU2-2
(c) S-CU2-1 (d) A8 [159]
图 9-23 本文建议模型与试验FRP应力分布对比
本文建议模型式(9.7)虽精度较好，但计算过程略显繁琐，且各个参数之间关系不够清晰，不便于工程人员使用。而张-叶-陆建议的模型 [158] 相对而言更清晰明了。因此，本文基于该模型形式提出相应的简化设计公式。
首先，由式(9.7b)
|
|
(9.8a) |
式中， 
为平均粘结应力。对上式进行整理不难得到，
|
|
(9.8b) |
对式(9.8b)和(9.7a)整理后可得，
|
|
(9.9) |
令 
，则可得曲线如图9-24所示。对曲线拟合得，
对于U型加固：
|
|
(9.10a) |
对于侧面粘贴加固：
|
|
(9.10b) |
考虑到式(9.10a)和(9.10b)形式很接近，为简化公式起见，可以将式(9.10a)改写成式(9.10b)乘以一个系数的形式，经验算发现系数取1.3时最为接近，即：
|
|
(9.10c) |
各曲线之间的关系如图9-24所示
图 9-24 拟合公式(9.10) 和数值结果对比
综上，受剪剥离时FRP的抗剪贡献的设计公式为，
|
|
(9.11a) |
|
|
|
(9.11b) |
|
|
|
(9.11c) |
|
|
|
(9.11d) |
式中，对于侧面粘贴加固 
，对于U型粘贴加固 
。
|
|
(9.11e) |
该式预测结果和试验结果对比如图9-25和表9-6，9-7所示，可见该公式预测的极限承载力和试验结果吻合良好，其精度和式(9.7)也差不多。且该公式的概念相对比较清晰，便于工程人员掌握，即：在剥离破坏情况下，FRP抗剪承载力由平均粘结强度 
和FRP粘贴面积 
相乘得到， 
主要与混凝土强度相关（式9.11b），而粘贴面积就等于斜裂缝上方FRP的面积。随着粘贴面积的增大，其粘贴效率会降低，这个降低效果用 
加以体现，粘贴面积越大， 
越小（式9.11d）。
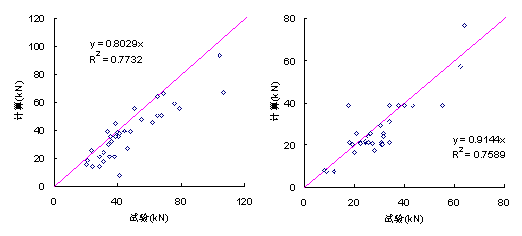
(a) U型粘贴加固 (b) 侧面粘贴加固
图
9-25式(9.11) 
与试验值比较
在不知道裂缝角度的情况下，可以假设斜裂缝的角度为45度，这样式(9.11a)可写作
|
|
(9.12) |
其预测结果如图9-26和表9-6，9-7所示，可见该模型明显偏于安全，超越概率小于3%，适于工程应用。
(a) U型粘贴加固 (b) 侧面粘贴加固
图
9.26式(9.12) 
与试验值比较
对于最常见的两种加固形式，即FRP纤维方向 
或 
时，式(9.12)可改写为：
|
|
(9.13a) |
|
|
|
(9.13b) |
9.6 小结
本章主要完成以下研究工作：
(1) 基于有限元分析，说明第五章提出的FRP-混凝土界面粘结-滑移本构模型可以用来分析抗剪加固剥离问题，并根据有限元分析结果讨论了FRP应力分布和斜裂缝形状的关系；
(2) 提出了3种有代表性的斜裂缝宽度分布模型。根据斜裂缝的宽度分布模型以及粘贴加固方式，提出了8种不同的FRP受剪剥离的简化计算模型；
(3) 通过非线性分析得到不同模型FRP的应力分布和发展规律，及其与斜裂缝形状、相对锚固长度之间的关系，讨论了受剪剥离破坏的机理；
(4) 得到不同模型平均粘结应力
与相对粘结长度 
之间的关系，并选取最不利的剥离破坏模型，建立了受剪承载力设计公式。与试验结果比较表明，本文建议公式和试验结果吻合较好，且偏于安全，可用于FRP受剪剥离承载力设计。
(5) 本章提出的FRP受剪剥离承载力计算方法，较好的反映了受剪剥离机理，参数意义明确，比现有的各个计算模型，无论是剥离承载力还是FRP应力分布规律都和试验结果吻合更好。