Distributed
TLDs in RC floors and their vibration reduction efficiency
L.P. Ye, X.Z., Lu, Z. Qu
Department of Civil Engineering, Tsinghua University, Beijing, 100084,
China
Key Laboratory of Structural Engineering and Vibration of China Education
Ministry
J. Q., Hou
Tsinghua Institute of Architectural Design, Beijing, 100084, China
Earthquake Engineering and Engineering Vibration, 2008, 7(1): 107-112.
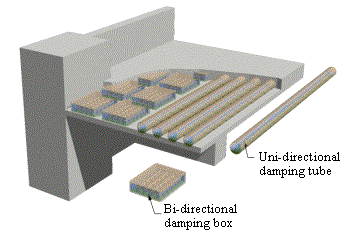
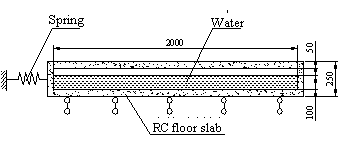
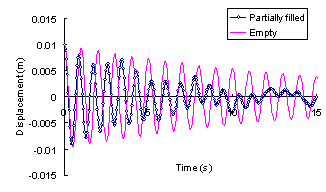
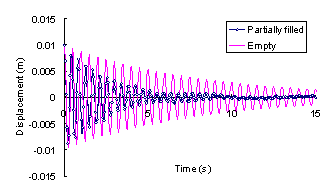
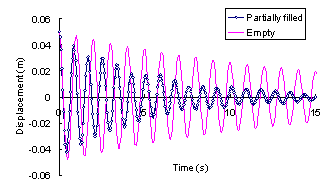
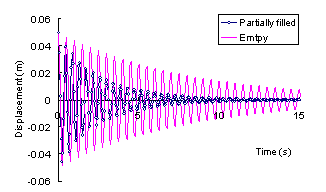
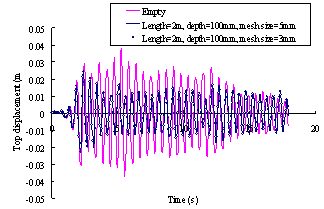
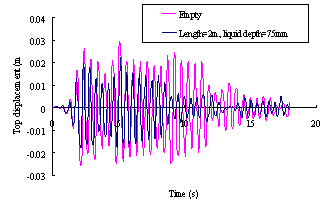
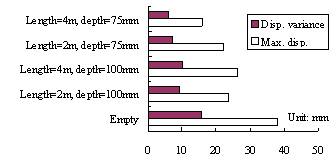
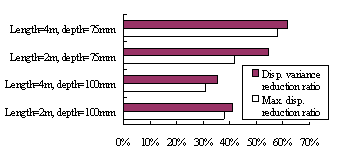
ABSTRACT: A novel distributed tuned liquid damper (DTLD) to reduce the vibration of structures is pro-posed in this paper. Its basic working principle is filling of the empty space inside the pipes or boxes of the cast-in-situ hollow reinforced concrete (RC) floor slabs with water or other damping liquid. Hence these pipes or boxes will work as a series of small TLDs inside the structure. Thus, no additional spaces are needed for TLDs whilst the damping ratio of the whole structure is obviously increased. Numerical simulation with the fluid-structure coupled effect is carried out to evaluate its vibration-reduction effect. The results indicate that distributed TLD can considerably increase the damping of the building and thus reduce the vibration. Some parameters influencing the vibration-reduction are also studied.
Keywords: distributed tuned liquid damper (DTLD), fluid-structure interaction (FSI), vibration reduction, hol-low floor slab