1. INTRODUCTION

The performance based design is the development trend of seismic design method (Bertero, 1994; Ye and Jing, 2002), but precise prediction for the nonlinear response of the structures under strong earthquake comes to be the most difficult issue. It is believed that the prediction of structural seismic response is not only associated with rational structure analysis model and method, but also depend on the seismic response dispersion of structures, which is significantly influenced by the variation of earthquake inputs and the elasto-plastic characteristics of structures themselves (Gupta and Krawinkler, 2000; Jing, 2002). The variation of earthquake inputs could be treated by statistical analysis of variant earthquakes, while the elasto-plastic characteristics of structures are related to many aspects, such as structural types, structural elements layout schemes and their load carrying capacity distribution. For a whole structure, the main factor that influences the dispersion of seismic response is the post-yield stiffness of structures, which also affects the strength demand, seismic stability and residual displacement (Iemura et al, 2006; Christopoulos and Pampanin, 2004). Jing Jie et al. (2003) found in shearing lumped mass MDOF models, even with an uniformly distributed strength and stiffness, the damage and deformation may concentrate in some story if their post-yield stiffness is not sufficiently large, which result in a larger response dispersion. This dispersion due to the poor elasto-plastic characteristics of structures may larger than the variant of ground motions, and makes it difficult to predict the seismic performance of structures undergoing severe earthquakes, which will significantly limits the development of performance based design method.   Hence, this paper presents the influence of post-yield stiffness of structures to the seismic response based on SDOF and MDOF systems via nonlinear time history analysis, and discusses the methods to increase the post-yield stiffness of structures which are illuminated by some practical examples.

2. SDOF SYSTEM

At present, the studies on SDOF systems are mainly focused on maximal elasto-plastic response spectrum and strength reduction factor R (Veletsos and Newmark,1960; Newmark,1973; Miranda and Bertero,1994). Most of the studies on post-yield stiffness are about the residual displacement after undergoing severe earthquakes, some researchers paid attention on the maximal elasto-plastic displacement and strength reduction factor R£¨Macrae and Kawashima, 1997; Borzi et al, 2001; Christopoulos et al, 2002£»Pampanin et al, 2003; Zhao and Tong, 2006£©. The major conclusion is that the SDOF system with positive post-yield stiffness could get stable vibration during earthquake and result in relatively smaller residual displacement, and the maximal displacement response could be reduced for short period systems.

Herein, the influence of the post-yield stiffness ratio g =k_y/k₀ to nonlinear seismic response of SDOF systems is discussed based on the SDOF model illustrated in Fig. 1, where k₀ is the initial stiffness, k_y is post-yield stiffness, g £½0 indicates the ideal elasto-plastic model, g >0 and g <0 indicate the positive and negative post-yield stiffness, respectively. The unloading stiffness and reloading stiffness of the model are all set to be k₀, which means the stiffness degradation factor a=0. Selecting two ideal elasto-plastic SDOF system (g£½0) to be the control SDOF system, of which the initial periods are T=0.5s and T=2.0 respectively, and the damping coefficients are set to be x=0.02 and the yield strength ratio a_y=F_y/G are all 0.2, where G is the total weight of the system. The earthquake records used for the nonlinear time history analysis are a series of 20 ground motions from Los Angeles area in America. The elastic displacement and acceleration response spectrum of the selected ground motions are illustrated in Fig.2, and the thick solid lines in Fig.2 are response spectrums of seldom occurred earthquake corresponding to 7, 8 and 9 degree earthquake intensities respectively according to Chinese code (GB50011-2001) for seismic design of buildings. Fig3(a,b) shows the influence of post-yield stiffness ratio g£½k_y/k₀ and the yield strength ratio a_y on the mean value of the maximum displacement resposnse d_max. It indicates that the negative post-yield stiffness will lead rapidly increasing of d_max when the yield strength ratio a_y is relatively small, especially for the short period system, therefore, a_y should be sufficiently large to control the d_max. For the systems with g>0, d_max is relatively smaller than that of the ideal elasto-plastic system. Furthermore, it can be seen from Fig.4a (T=0.5s, x£½0.02, a_y=0.2G) that d_max decreases with the increasing of g  when g >0. If g <0, d_max rapidly increases with the decreasing of g, and when g=-0.01, d_max trends to be infinite which indicates the system collapsed. From Fig.4b(T=2.0s, x£½0.02, a_y=0.2G), the change of d_max are very small when g>0. If g <0, d_max also rapidly increases with the decreasing of g. Fig.5 indicates the influence of post-yield stiffness to residual displacement d_r,max of the systems. For T=0.5s system (Fig.5a), d_r,max and its standard deviation decrease with increasing of g when g >0. For T=2.0s system (Fig.5b), d_r,max and its standard deviation decrease with increasing of g  when g >0, but the change is much slower as compared the T=0.5s system. When g=0.5, d_r,max is quite close to zero. Therefore, if the larger post-yield stiffness is, the smaller of residual displacement is. It is due to that the post-yield stiffness means the recovering capacity of the structures.

It is believed that from the above analysis, sufficient post-yield stiffness will reduce the maximum displacement response for short period structures; for mid and long period structures, the increasing of post-yield stiffness makes slightly increasing of maximum displacement response. The increasing of post-yield stiffness will also reduce the residual displacement. For the systems with negative post-yield stiffness, maximum displacement and residual displacement increase rapidly with decreasing of post-yield stiffness ratio.

3. MAXIMUM STORY DRIFT OF MDOF SYSTEM

A ten-story lumped mass model is taken as an example to study the influence of post-yield stiffness to MDOF system. The relationship between story shear and drift is also same as Fig.1. The height, weight and initial elastic shear stiffness of each story are 3m, 5000ton and 1¡Á10⁹N/m, respectively. The fundamental period is 0.9s and the damping coefficient is set to be 2.1% which is only proportional to the mass matrix M. A series of 40 ground motions are downloaded from PEER with PGA between 0.1g and 2.0g. These ground motions represent a wide variety of seismic characteristics. The factors considered herein are as follows: (1) the PGA of each ground motion is set from 0.1g to 1.0g with the interval of 0.1g; (2) the story yield drift D_y is set to be 1/1500, 1/500, 1/250 and infinite (pure elastic case), respectively; (3) the story post-yield stiffness ratio is given by 0.0£¬0.05£¬0.1£¬0.15£¬0.2£¬0.4£¬0.6£¬0.8£¬1.0(pure elastic case), respectively. For convenience, the mean values of the maximum story drifts  and their standard deviations  computed by 40 earthquakes is compared and illustrated in Fig.6 for the MDOF systems with different D_y and g.  From Fig.6, following conclusions are obtained for ideal elasto-plastic MDOF systems: (1)  increases with increasing of PGA, especially when PGA is large than 0.6g,  are over 1/50 which is the limitation of the inelastic story drift according to Chinese code; (2) the trend of increasing of with increasing of PGA is basically bilinear. increases slowly when PGA is relatively small, while  increases rapidly when PGA is sufficiently large; (3) of ideal elasto-plastic systems decrease with increasing of D_y under a constant PGA, which means that the increasing of yield strength will reduce the inelastic response; and(4) for a constant D_y, when PGA is relatively small, the is also relatively small, but increases rapidly with the increasing of PGA. If PGA is sufficiently large, will be 4~6 times larger than the values of cases under minor PGA earthquakes. It means that the dispersion of the inelastic response of ideal elasto-plastic system is quite large when the story yielding appears. But this situation could be delayed if the D_y increases to the value when  changes slightly. Therefore, the inelastic seismic response is sensitive to the story yielding for ideal elasto-plastic systems.

In Fig.6, the mean value and standard deviation of maximum story-drifts of positive post-yield stiffness MDOF systems are much smaller than ideal elasto-plastic systems, so their curves are too close to each other, therefore, they are independently shown in Fig.7, in which only positive post-yield stiffness MDOF systems are given. From Fig.7, following conclusions are obtained for positive post-yield stiffness MDOF systems: (1) for a given post-yield stiffness ratio g , will increase linearly with increasing of PGA; (2) decreases with increasing of g and will get closer to the value of the elastic system. When g is larger than 0.4, the values of are quite close to the value of the elastic system; and (3) if under a certain PGA and D_y, the standard deviation  decreases with the increasing of post-yield stiffness ratio g . will be slightly decreased when g is large than 0.4 because at such situation, the response dispersion is mainly due to the dispersion of earthquake input. From above results, it is found that the maximum story drifts and the deviation of ideal elasto-plastic systems are all much larger than those with positive post-yield stiffness. Therefore, rational positive post-yield stiffness will give better seismic performance.

4. DUCTILITY AND ENERGY DISTRIBUTION OF MDOF SYSTEM

In this section, the same shearing lumped mass model as previous section is still used to investigate ductility and accumulative hysteretic energy distribution. The degrees of the MDOF system are 5, 10, 20 and 30, respectively; the coefficient of post-yield stiffness of stories is set to be 0.05, 0.1, 0.2, 0.3, 0.5 and 0.75, respectively and the strength reduction factor is taken to be 1, 2, 4, 6 and 8. All the cases are computed by time history analysis using the El-centro NS earthquake record. The ductility factors and accumulative hysteretic energy distribution are illustrated in Fig.8 for some of analyzed cases. It indicates that the distributions of ductility factors and accumulative hysteretic energy are obviously concentrated in some stories when post-yield stiffness ratio is relatively small (g<0.5). And the increasing of degrees of MDOF systems aggravates the concentricity. If g is sufficiently large (g ¡Ý0.5), the distributions of ductility factors trend to be uniform and the concentration of hysteretic energy disappears. Therefore, large post-yield stiffness can result in uniform distribution of ductility and accumulative hysteretic energy and reduce the maximum story drift of the systems evidently as well.

5 METHODS OF INCREASING POST-YIELD STIFFNESS OF STRUCTURES

As discussed above, appropriate post-yield stiffness of the structure is significantly important to the performance based design. Nakashima et al (1996) suggested post-yield stiffness ratio g  >0.75, Jing (2002) suggested g >0.5, and Connor et al£¨1997£©suggested g >0.33, respectively. To increasing post-yield stiffness, Pettinga et al (2007) suggested: (1) using reinforcement materials with hardening features; (2) re-designing the section geometry and properties of primary seismic-resisting elements; and (3) introducing a secondary inelastic system in parallel with the primary system. Considering that the structure system is made up with many different kinds of elements, so the sufficient lateral post-yield stiffness of the structure system could be achieved by sequentially yielding of different structural elements. Therefore, many researchers proposed a series of concepts to achieve a structural system with positive post-yield stiffness, which including rigid-flexible structure, damage control structure and dual seismic structure (Nakashima et al, 1996; Connor et al, 1997; Harada and Akiyama, 1998; Pettinga et al, 2007). The more effective way to increase the post-yield stiffness is to let parts or all of the secondary structural elements yield before the primary part of the structures does, and the system capacity design method was proposed by Ye (2004) based on this concept. The system capacity design method indicate that a seismic structural system must have primary structural members or substructures to control the seismic response of the whole structure, which could provide a sufficient lateral post-yield stiffness of the structure. Columns, shear walls, tubes and mega-frame can be used as primary structural members or substructures. All these members or substructures should keep their strengths and stiffnesses without deterioration before other secondary structural elements yield or even failed. The post-yield stiffness of seismic structures can be estimated by pushover analysis, though the result is not totally in accordance with the actually seismic response undergoing earthquakes. Some practical examples are presented below to show the different ways to increasing the post-yield stiffness by pushover analysis.

Fig.9 gives results of two 6-story RC frames, one is ordinary frame (OF) and another is the same frame but reinforcement in columns is replaced by high strength steel strand (PF). For ordinary frames designed by strong-column-weak-beam principle, it shows a little bit post-yield stiffness before the base column hinges appear due to the yielding of the beams, but the post-yield stiffness would be completely lost if the hinges at column feet appear. For the PF frame, as shown in Fig.9, the failure mechanism is greatly delayed because of the absence of plastic hinges at the base column. (Ye et al, 2006). A steel frame structure using buckling resistance braces (BRB) is shown in Fig.10. The strength of BRB, beams and columns are 235MPa, 345MPa and 420MPa, respectively. During the earthquake, BRB usually yield firstly because of the large axial forces in them and low yield strength, then the beams yield, and finally the columns. Fig.11 shows another example of frame-shear wall structure. For the one without coupling beams, it gives the first phase of the post-yield stiffness by yielding in sequence of frame beams. After the base of shear wall yields, the load carried by wall would increase slightly and more frame beams would yield, thus the relatively smaller phase of the post-yield stiffness appears. For the one with coupling beams, both two phases of the post-yield stiffness would be much larger than that without coupling beams. Hence, structural systems with multiple seismic subsystems could get better seismic performance. Finally, a practical hybrid structure of steel and reinforced concrete is analyzed as shown in Fig.12. The core tube is composed of four RC sub-tubes connected by steel, SRC and RC coupling beams. The outer frame is steel. As illustrated in Fig.12, this practical structure has multiple seismic substructures and shows great enhanced post-yield stiffness.

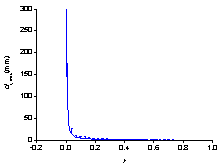
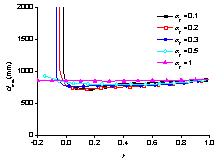
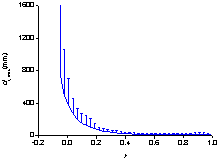
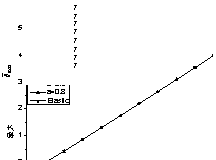
6. CONCLUSIONS

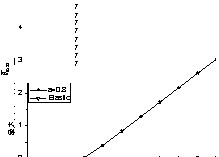
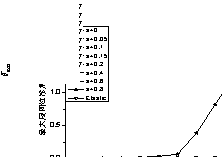
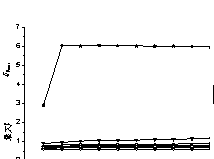
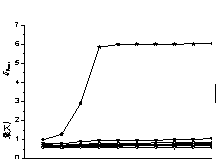
This paper studied the influence of post-yield stiffness to seismic response of structures based on SDOF and MDOF systems by inelastic time history analysis. According to the results, it indicates that sufficient post-yield stiffness is quite necessary for performance based design to control the seismic performances. Variant ways of increasing the post-yield performance of structures are also concluded as, (1) using different reinforcement materials with hardening stress¨Cstrain behavior, (2) re-designing the section geometry and properties of primary seismic-resisting elements or introducing a inelastic secondary systems to act in parallel with the primary system, (3) the more important thing to improve structural post-yield performance is to provide the structural system with primary seismic members or substructures and clarify the load capacity levels of different structural members. Finally, some examples are used to illuminate the post-yield performance of different structures by pushover analysis.

ACKNOWLEDGEMENT

The research presented in this paper was funded by the National Key Project of Scientific and Technical Supporting Programs by Ministry of Science & Technology of China (2006BAK01A02-09).

REFERENCES

Bertero, V.V. (1994). Major issues and future directions in earthquake-resistant design. Proceeding of 10th World Conference on Earthquake Engineering. Madrid, 6407-6444.

Ye, L.P. and Jing, J. (2002). Study on the structural seismic design methods. Proc. 6^th National Conference on Earthquake Engineering, Nanjing, China, 419-429.

Gupta, A. and Krawinkler, H. (2000). Behavior of ductile SMRFs at various seismic hazard levels. J. Structural Engineering, ASEC 126:1, 98-107.

Jing, J. (2002). Studies on displacement-based seismic design for dual structures. Thesis for PhD, Tsinghua University, Beijing, China.

Iemura, H., Takahashi, Y. and Sogabe, N. (2006).Two-level seismic design method using post-yield stiffness and its application to unbonded bar reinforced concrete piers. Structural Engineering/Earthquake Engineering 23:1, 109-116.

Christopoulos, C. and Pampanin, S. (2004). Towards performance-based seismic design of MDOF structures with explicit consideration of residual deformations. J. of Earthquake Technology 41:1, 53-73.

Jing, J,,Ye, L.P. and Qian, J.R. (2003). Inelastic seismic response of lumped mass MDOF systems based on energy concept. Engineering Mechanics 20:3, 31-37.

Veletsos, A.S. and Newmark, (1960). N.M. Effect of inelastic behavior on the response of simple system to earthquake motion. Proc. 2^nd World Conference on Earthquake Engineering, Tokyo, 895~912.

Newmark, N.M. and Hall, W.J. (1973). A rational approach of seismic design standards for structures. Proc. 5^th World Conference on Earthquake Engineering, Roma, 2266-2277.

Miranda, E. and Bertero, V. (1994). Evaluation of strength reduction factors for earthquake-resistant design. Earthquake Spectra, 10:2, 357-379.

MacRae, G.A. and Kawashima, K. (1997). Post-earthquake residual displacements of bilinear oscillators. Earthquake Engineering and Structural Dynamics 26:7, 701-716.

Borzi, B., Calvi, G.M., Elnashai, A.S., Faccioli, E. and Bommer, J. (2001). Inelastic spectra for displacement-based seismic design. Soil Dynamics and Earthquake Engineering 21:1, 47-61.

Christopoulos, C., Filiatrault, A. and Folz, B. (2002). Seismic response of self-centring hysteretic SDOF systems. Earthquake Engineering & Structural Dynamics 31:5, 1131-1150.

Pampanin, S., Christopoulos, C. and Priestley, M.J.N. (2003). Performance-based seismic response of frame structures including residual deformations: Part I: single-degree of freedom systems. J. Earthquake Engineering 7:1, 97-118.

Zhao, Y.F. and Tong, S.G. (2006). Seismic force modification factor s for structures with modified-Clough hysteretic model. China Civil Engineering Journal 39:10, 34-41.

GB50011-2001. (2001). Code for seismic design of buildings. China Architecture Industry Press, Beijing.

Nakashima, M., Saburi, K. and Tsuji, B. (1996). Energy input and dissipation behaviour of structures with hysteretic dampers. Earthquake Engineering & Structural Dynamics 25:5, 483-496.

Connor, J.J., Wada, A., Iwata, M., Huang, Y.H. (1997). Damage-controlled structures. I: Preliminary design methodology for seismically active regions. Journal of Structural Engineering 123:4, 423-431.

Pettinga, D., Christopoulos, C., Pampanin S. and Priestley N. (2007). Effectiveness of simple approaches in mitigating residual deformations in buildings. Earthquake Engineering & Structural Dynamics 36:12, 1763-1783.

Harada, Y. and Akiyama, H. (1998). Seismic design of flexible-stiff mixed frame with energy concentration. Engineering Structures 20:12, 1039-1044.

Ye, L.P. (2004). Structure system capacity design approach and performance/displacement-based seismic design. Building Structure 34:6, 10-14.

Ye, L.P., Asad, U.Q., Ma, Q.L. and Lu, X.Z. (2006). Study on failure mechanism and seismic performance of passive control RC frame against earthquake. Earthquake Resistant Engineering 28:1, 8~24.