1.       Introduction

One of the primary tasks in performance-/displacement-based seismic design is to accurately determine the structural responses under strong earthquakes especially during the inelastic stage. The nonlinear time-history analysis (THA) method is able to accurately predict the structural behavior under strong earthquakes. However it is impractical to extend THA to engineering application due to the uncertainty of input earthquake records and the associated high computational cost. In consequence, the nonlinear static procedure (pushover analysis) has been popularly used as a simplified and approximate method to predict inelastic behavior of structures. The pushover analysis method has been adopted by ATC-40 (1996), FEMA273, 274 (1997) and FEMA356 (2000). The method has also been recommended by Chinese building code GB50011-2001 (2001) by which the structural inelastic deformations under strong earthquakes can be evaluated.

       In most current pushover procedures, the first step is to apply a lateral load with an invariant pattern over the structural height. This load is monotonically increased until the failure or collapse of the system which is of multi degrees-of-freedom (MDOF). The relationship between the base shear and the roof displacement can then be obtained for the system. This is followed by converting such a relationship to the force-deformation relation of an equivalent single degree-of-freedom (SDOF) system. The analysis of the equivalent SDOF system would lead to the target displacement of the original MDOF system under earthquake together with the structural inelastic deformation. In the pushover analysis, the selection of an appropriate load pattern is a key issue (Krawinkler and Seneviratna 1998; Fajfar and Gaspersic 1996; Moghadam and Tso 2000; Requena and Ayala 2000). For the purpose of discussion, the load patterns as suggested by FEMA356 (2000) are briefly enumerated herein where one of the load patterns shall be selected from each of the following two groups:

Group 1 consists of three load patterns designated as G1-1, G1-2 and G1-3:

G1-1: A vertical distribution proportional to the values of w_ih_i^k at each storey. Here, w_i is the weight of the ith storey; h_i is the height of the floor level i measured from the base; k is a factor determined by the structural fundamental vibration period T. Note that the use of this distribution is only permitted when more than 75% of the total mass participates in the fundamental mode in the direction concerned.

G1-2: A vertical distribution proportional to the shape of the fundamental mode in the direction concerned. The applicability of this distribution is identical to that as specified in G1-1.

G1-3: A vertical distribution proportional to the storey shear force distribution, which is calculated by combining modal responses from a response spectrum analysis of the building. In the process of modal response combination, sufficient modes capturing at least 90% of the total building mass must be included and the appropriate ground motion spectrum should be used.

Group 2 covers two load patterns designated as G2-1 and G2-2:

G2-1: A uniform distribution consisting of lateral forces at each storey level which is proportional to the total mass of the corresponding level.

G2-2: An adaptive load distribution that changes as the structure is displaced. This distribution shall be modified from the original one using a procedure that considers the properties of the yielded structure. Although the use of an adaptive load pattern may yield more consistent results with the characteristics of the concerned building, it requires more analysis effort and is less convenient as compared to the invariant load pattern.

In the pushover analysis with the above mentioned invariant load patterns, only the effect of the first structural vibration mode is taken into account. The influence of higher vibration modes is not considered. Hence the method is only applicable to low- to medium-rise structures which are governed primarily by the first vibration mode (Albanesi et al. 2000; Bracci et al. 1997; Gupta and Krawinkler 2000).

In order to consider the effect of higher vibration modes, Chopra and Goel (2002) proposed a new pushover procedure based on the modal decoupling response spectrum method. The procedure is referred to as the Modal Pushover Analysis (MPA) which is summarized in the following steps:

Step 1. Compute the natural frequencies, w_n,  and the corresponding modes, f_n, of linear elastic vibration of the MDOF system.

Step 2. For the ith-mode (i=1, n), establish the base-shear versus roof-displacement (V_bi-u_ri) pushover curve under the force distribution [m]{f_i}.

Step 3. Idealize the pushover curve using a bilinear representation.

Step 4. Convert the idealized pushover curve to the force-deformation relation for the equivalent inelastic SDOF system.

Step 5. Compute the peak deformation, D_i, of the SDOF system with the force-deformation relation obtained in Step 4. This is done by solving the dynamic equation of the SDOF system.

Step 6. Convert the peak deformation of the SDOF system to the peak roof displacement u_rio of the MDOF system (target displacement).

Step 7. At u_rio, estimate the peak value r_io of any structural response of the original MDOF system.

Step 8. Repeat Steps 2 to 7 for as many ¡°modes¡± as required for sufficient accuracy. Typically, the first two or three ¡°modes¡± will suffice.

Step 9. Determine the total response by combining the peak ¡°modal¡± responses using the SRSS (Square Root of the Sum of the Squares) combination rule.

In the MPA procedure, the fundamental assumption is that the coupling of structural responses due to different modes is neglected after the structure enters the inelastic stage. Such an assumption unfortunately makes the MPA procedure less rigorous for estimating structural responses of inelastic systems. This in turn may cause estimation errors against the ¡°exact¡± solutions of nonlinear time-history analysis. However the decoupling nature of the MPA allows an effective and satisfactory estimation of the structural responses particularly for high-rise structures influenced by higher order modes (Chopra and Goel 2002). This cannot be achieved by the pushover procedure with invariant load patterns. Being advantageous in application over the pushover procedure, the MPA is also simple in concept and effective in computation.

Also evaluated in Chopra and Goel¡¯s study (2002) was the peak inelastic response of a 9-storey steel building predicted by the MPA procedure. The comparison between the predicted results and those of a rigorous nonlinear time history analysis demonstrated that the MPA is accurate enough for practical application in building evaluation and design. Chintanapakdee and Chopra (2003) applied the MPA procedure to a wide range of frame buildings and ground motion ensembles. This has led to the development of a practical version of the MPA procedure to estimate seismic demands for inelastic systems with earthquake hazard defined by a median design spectrum for elastic systems. In addition to the application of the MPA procedure in symmetric-plan systems, the method has also been extended by Chopra and Goel (2004) to estimate seismic demands for unsymmetric-plan buildings. The results showed that the MPA is generally accurate for unsymmetric-plan systems to a similar degree as it was for a symmetric building. Based on the MPA procedure, Han and Chopra (2006) further developed an approximate incremental dynamic analysis (IDA) procedure. An estimation of the seismic demands of buildings with different heights demonstrated a good accuracy of the approximate procedure. Furthermore, a procedure similar to the MPA has been developed by Chou and Uang (2003) to evaluate the absorbed energy (an alternative index to response quantities) and its distribution over the structural height in multistorey frame buildings.

The applications of MPA to date, as discussed above, have been focused on frame structures only. In modern construction practices, frame-shear-wall systems are widely used in medium- to high-rise buildings. Such a system exhibits different deformation characteristics from the frame structures. It is therefore necessary to extend the current research activity to implement the MPA to frame-shear-wall structures. In this paper, two RC frame-shear-wall structures of 10 and 18 stories are analyzed to evaluate the performance of the MPA method and pushover procedures with invariant load patterns. The analysis results are compared to the ¡°exact¡± solutions due to the nonlinear dynamic time-history analysis. Based on the validated nonlinear analytical models, the solutions of nonlinear dynamic time-history analysis are considered as the most accurate results (i.e. the ¡°exact¡± solutions) to describe the complex nonlinear behavior of structures under earthquake. These ¡°exact¡± solutions are often used as benchmark solutions as adopted also by experts in the field (Chopra and Goel 2002; Jan et al. 2004).

2.       Analytical model

In most regions of China, frame-shear-wall systems are usually employed for buildings of more than 8 stories. In this study, a 10-storey and 18-storey RC frame-shear-wall structures are analyzed representing typical medium- and high-rise buildings. The two structures are designed based on the Chinese building code GB50011-2001 (2001). Figure 1 shows the plan view of a typical building storey for both structures. The overall height of the 10- and 18-storey structures is 65.7m and 36.9m respectively. The ground storey is 4.5m in height and the remaining stories are 3.6m. The designed seismic intensity for both structures is 8 degree and the site classification is type II. The member dimensions and reinforcement details are given in Tables 1 and 2, for the two structures respectively. For the 10-storey structure, 80% of the total mass participates in the fundamental mode; and 90% and 95% in the first two and three modes respectively. For the 18-storey structure, the corresponding percentages of participation are 68%, 85% and 94% respectively. Based on the above percentages of the total mass participation, the selected 10-storey structure is considered to represent typical medium-rise buildings of which the dynamic responses are governed by the first mode. By the same token, the 18-storey structure is regarded as representing high-rise buildings which are largely influenced by higher-order modes under earthquake.

Figure 1 also illustrates that the shear walls are arranged in the Y-direction. To analyze the behavior of the frame-shear-wall structures, a simplified planar system in the Y-direction is thus considered. The system is idealized by a combination of a frame and a shear wall which are hinge connected by horizontal rigid links at storey levels. This is to simulate horizontal compatibility of frame and shear wall originally provided by the floor slabs. The planar system (Figure 2) is modeled by the general purpose FEA software MSC.MARC (2005), in which the frame members (beams and columns) are modeled by fiber model elements (Figure 3) and the shear-wall members (walls and coupling beams) by multi-layer-shell-elements (Figure 4) (Ye et al. 2006). Note that boundary elements of the wall are also modeled by multi-layer-shell-elements. Details of the analytical models are given in Appendix A.

3.       Analysis details

In the present analysis, the performances of the pushover procedures with invariant load patterns and the MPA method are evaluated. This is achieved by comparing their prediction results with the ¡°exact¡± solutions due to the nonlinear dynamic time-history analysis.

3.1.    Pushover analysis

For the pushover analysis, two different lateral load patterns are chosen based on FEMA356 (2000): (1) G1-3, also referred to as the ¡°SRSS pattern¡± because of the use of SRSS in the process of modal response combination. Such a pattern is determined by including the first three modes on the average pseudo-acceleration spectrum of the selected earthquake records. (2) G2-1, the uniform pattern proportional to the total mass at each storey level.

3.2.    MPA procedure

Research on MPA to date has been focused on frame structures. Little work is found in the application of MPA to frame-shear-wall structures and the consideration of mass distribution has not been well documented. As a result, this becomes a challenging issue in the present study on 10- and 18-storey frame-shear-wall structures.

As an initial attempt, the mass of the beam, column and wall is assumed to be distributed over the geometric shape of each element. This leads to an original analytical model referred to as the ¡°distributed-mass model¡± (DMM), in which the mass of each storey is distributed over the structural height instead of being concentrated at each floor level. Correspondingly, the inertial forces are also distributed over the structural height because the mass is distributed over the structural members especially the vertical members. The DMM is thought to be the most accurate analytical model which can reflect the actual situation of the structure. However the following problem is presented during the process of implementing the MPA procedure on the DMM. For the ith-mode, the pushover curve of base shear-roof displacement of the original MDOF system is first established and then used to obtain the force-deformation relation of the equivalent inelastic SDOF system. The initial slope or the elastic stiffness of the force-deformation relation of the SDOF system represents the angular frequency w_pi of the original structure. Note that the actual angular frequency w_i (for the ith-mode) of the original structure can also be determined directly based on a structural modal analysis. Theoretically the resulting w_pi and w_i should be identical. However the analysis of the 10- and 18-storey structures demonstrates that the errors in w_pi with respect to w_i increase significantly with an increase in the order of mode. This is presented in Table 3. Such an error may cause large deviations in the estimation of structural responses due to higher-order modes.

The errors in w_pi are attributed to the consideration of the distributed inertial forces over the structural height. In the pushover procedures including the MPA procedure, however, the inertial forces are usually represented by the static lateral loads applied at floor levels. This requires the use of a so-called ¡°lumped-mass model¡± (LMM) where the mass of the column and wall is considered through a mass member at each floor level. This leads to the proposed analytical model, or the LMM. The significantly reduced errors in w_pi with respect to w_i (shown in Table 4) verify the suitability of the LMM for the MPA procedure.

       In should be noted that although the estimation errors are reduced, the LMM is more approximate in nature as compared to the DMM. Therefore the appropriateness of using the LMM in frame-shear-wall structures should be examined. It is noticed that the actual angular frequencies w_i of the original structure are almost identically determined in the DMM (Table 3) and the LMM (Table 4) for both 10-storey and 18-stroey structures. This suggests that both models are able to accurately reflect the actual structural vibration characteristics.

Further, a nonlinear time-history analysis is performed for both models under two selected earthquake records (as detailed in Section 3.3 below). Again the structural response results (including the storey drift, the floor displacement and the storey shear force) due to the two models are shown to be similar. This is presented in Tables 5 and 6 for earthquake records No. 1 and No. 2, respectively. The comparison indicates that the LMM is accurate enough to predict the structural seismic responses. As such, the LMM (¡°lumped-mass model¡±) is used throughout the following analysis including traditional pushover, MPA as well as nonlinear time-history.

3.3.    Nonlinear time-history analysis

During the nonlinear dynamic time-history analysis, the Rayleigh damping of 5% is used. Note that the P-D   effects are taken into account in all analyses including traditional pushover, MPA as well as nonlinear time-history.

For the time-history analysis, the actual earthquake records are required as the input of ground motions. In this study, a group of ten strong earthquake records are selected from the PEER database (2005), as listed in Table 7. During the analysis, all these earthquake records are normalized by the peak ground acceleration (PGA). In the present study, three levels of earthquake intensity are considered viz the minor, moderate and major levels. According to the Chinese Code GB50011-2001 (2001), the corresponding PGAs are set as 70gal, 200gal, 400gal, respectively, to achieve the three intensity levels. This is under the condition that the designed seismic intensity for the 10- and 18-storey structures is assumed to be 8 degree. The pseudo-acceleration spectrums of the ten normalized earthquake records and the average spectrum are shown in Figure 5. Also included in the figure is the design spectrum specified in GB50011-2001 (2001).

4.       Analytical results

       The structural responses including the storey drift, the floor displacement and the storey shear force under three earthquake intensity levels are predicted by the MPA and the traditional pushover methods. The predictions are then compared with the results due to nonlinear dynamic time-history analysis (THA), which is considered to produce ¡°exact¡± structural seismic responses. For THA, a set of results is obtained under each earthquake record. This is the same for all the pushover analyses including MPA procedures. Note that all the results presented herein are the median values under 10 normalized earthquake records for both THA and pushover analysis if not specified elsewhere.

4.1.    Peak storey drift

Under the minor, moderate and major earthquake intensity levels, the peak storey drift over the structural height are presented in Figures 6 and 7 respectively for the 10- and 18-storey frame-shear-wall structures. Included in the figures are the predictions due to THA as an exact measure. The predictions due to the pushover procedure are obtained using the SRSS and uniform patterns. Also included in the figures are the MPA results for the first mode (1 Mode), the first two modes (2 Modes) as well as the first three modes (3 Modes). To illustrate the absolute differences under the three earthquake intensity levels, the prediction errors (in percentage) with respect to the THA results are also plotted.

       For the 10-storey structure under three different earthquake levels, the differences in the storey drift due to the pushover and the MPA methods increase over the structural height. This is presented in Figure 6. In comparison to the exact solutions of THA, all the predictions appear to underestimate the storey drift except those due to the SRSS load pattern under the moderate and major earthquake levels (above 2^nd floor) (Figures 6(b) and (c)). The most underestimated predictions are those of pushover procedure with uniform load pattern and MPA including the first mode (1 Mode). The MPA prediction including the first two modes (2 Modes) improves the accuracy especially for the upper stories. However no further improvement is achieved when the first three modes (3 Modes) are included. This is because 80% of the total mass is participated in the fundamental mode for the 10-storey structure. Hence the structure is governed primarily by the first mode responses and the contributions of the higher-order modes are not significant (90% and 95% total mass participations in the first two and three modes respectively). In general, the SRSS pattern produces more accurate results than the other prediction procedures. The slight overestimation of the SRSS pattern under the moderate and major earthquake levels is considered safe in engineering practice. The comparison on the storey drift indicates that the pushover procedure with SRSS pattern is ideal for medium-rise frame-shear-wall structures in which the higher-order modes do not have a significant influence.

For the 18-storey structure, Figure 7 presents the storey drifts over the structural height for the three earthquake levels. Compared to the findings from the 10-storey structure, both the pushover analysis with uniform load pattern and the MPA including the first mode overly underestimate the storey drift. This is due to the fact that both these prediction methods ignore the effect of higher order modes. Dissimilar to the predictions of the 10-storey structure, the pushover analysis with SRSS pattern provides an accurate estimation for the lower stories. However its prediction starts to deviate from the THA at and above the middle storey which is primarily governed by the higher order modes. This is because in the determination of the SRSS pattern, the effect of higher-order mode on the structural response is taken into account by a fixed proportion which reflects the maximum combined and instantaneous modal effects. Such a SRSS pattern remains unchanged during the entire pushover analysis. Comparing to the results of pushover analysis and MPA 1 Mode, a substantial improvement is achieved in predictions by the MPA when the response contributions of the second mode is included. This is especially true for upper stories. A further improvement can be resulted by including all first three modes in the MPA procedure. Different to the 10-storey structure, the total mass participation in the first mode is only 68% for the 18-storey counterpart. This, together with the 85% and 94% participations in the first two and three modes, indicates that the structure is largely influenced by higher-order modes under earthquake. This further suggests that for high-rise buildings, the MPA procedure including at least the first two modes should be used.

As all the results presented in Figures 6 and 7 are the median values under 10 normalized earthquake records (for THA and all the pushover analyses), more statistical representation of results is needed to evaluate data dispersion. Figure 8 shows the median and 84 percentiles (median plus one standard deviation) for both THA and pushover analysis with SRSS pattern which gives the best prediction of peak storey drift for 10-storey structure. Similarly, the median and 84 percentile results for both THA and MPA including the first three modes, which appears to be the most satisfactory procedure in the case of 18-storey structure, are shown in Figure 9. The data dispersion using THA is a little higher than the corresponding pushover results in both cases. These findings provide a measure of confidence in the general predictive abilities of the pushover procedures.

4.2.    Peak floor displacement

Presented in Figures 10 and 11 respectively are the peak floor displacements for the 10- and 18-storey structures under the minor, moderate and major earthquake intensity levels. The displacements due to different prediction methods are plotted over the structural height, together with the prediction errors with respect to the THA results.

For the 10-storey structure, Figure 10 shows that all the predicted peak floor displacement increases almost linearly with the storey height. The overall predictions due to different methods show similar characteristics to those obtained for the peak storey drift.

For the 18-storey structure, the phenomenon of linearly increased displacement is still valid for the prediction methods (pushover procedure and MPA 1 Mode) where the effect of higher-order modes is neglected. However this is not the case for MPA 2 Modes and 3 Modes because of the inclusion of higher-order modes. While the pushover procedure with uniform pattern and MPA 1 Mode underestimate the peak floor displacement, the prediction due to SRSS pattern is overestimated in particular for the higher stories. Although MPA 2 Modes and 3 Modes overestimate the displacement around the middle storey, they are considered superior methods particularly for the case of major earthquake (Figure 11(c)).

Shown in Figures 12 and 13 respectively are the median and 84 percentiles for both THA and a specific pushover analysis (SRSS pattern for 10-storey and MPA including the first three modes for 18-storey structure). It can be seen from the figures that the data dispersion using THA is a little higher than the corresponding pushover analysis results for both medium- and high-rise structures.

4.3.    Peak storey shear

The peak storey shear over the structural height under the minor, moderate and major earthquake levels are plotted in Figures 10 and 11 for the 10- and 18-storey structures respectively. Also included in the figures are the prediction errors.

       For the 10-storey structure as shown in Figure 14, the pushover analysis with uniform load pattern produces a linear floor versus storey shear relationship which is definitely unable to capture the true shear force behavior as predicted by the THA. The SRSS load pattern and the MPA 1 Mode underestimate the shear force to a different degree especially for the lower stories. This is particular evident for the case of major earthquake. The MPA 2 Modes and 3 Modes have shown to achieve the most satisfactory predictions than the other methods. In addition, the inclusion of a higher mode (3 Modes) does not improve the accuracy of prediction because the medium-rise structure is primarily governed by the first mode responses.

A significant difference is noticed in Figure 15 for the 18-storey structure in that the pushover analysis with uniform and SRSS load patterns as well as the MPA 1 Mode overly underestimate the storey shear force. Although the prediction is much improved by the MPA 2 Modes, in particular for the lower and upper stories, this method is still inadequate to offer a reliable solution for the middle stories. It is obvious that the inclusion of a higher mode (MPA 3 Modes) is vitally important for high-rise structures in achieving a satisfactory solution.

Presented in Figures 16 and 17 respectively are the median and 84 percentiles for both THA and a specific pushover analysis (MPA including the first three modes for both 10-storey and 18-storey structures which gives the best prediction of peak storey shear in both cases). Again similar findings as outlined in Sections 4.1 and 4.2 are achieved in relation to data dispersion.

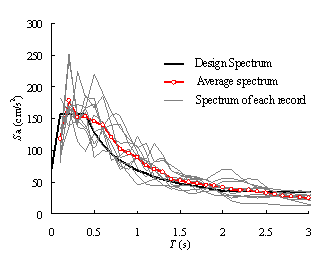
5.       Conclusion

In this study, two RC frame-shear-wall structures of 10 and 18 stories are analyzed to evaluate the performance of the nonlinear static prediction procedures including the MPA method and the pushover procedures with invariant load patterns. In comparison with the ¡®exact¡¯ solution of nonlinear dynamic time-history analysis, these procedures appear to perform similarly for frame-shear-wall structures as for the frame systems although the two systems have different deformation characteristics.

Through a comprehensive estimation of the structural responses including the peak values of storey drift, floor displacement and storey shear under various earthquake intensity levels, the following specific conclusions can be drawn:

(1) In the process of implementing the MPA procedure in frame-shear-wall structures, the ¡°lumped-mass model¡± (LMM) should be used in numerical analysis to obtain a more reasonable force-deformation relation of the equivalent inelastic SDOF system for the ith-mode.

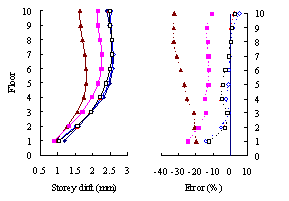
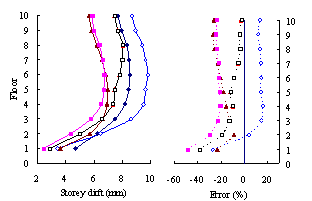
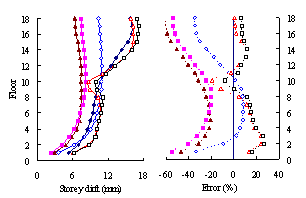
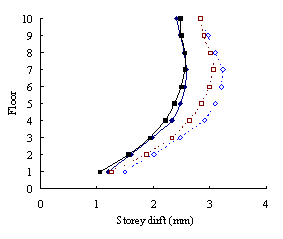
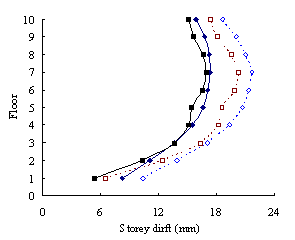
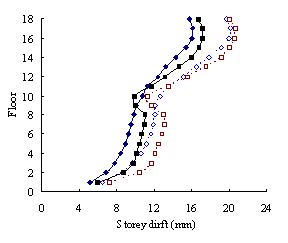
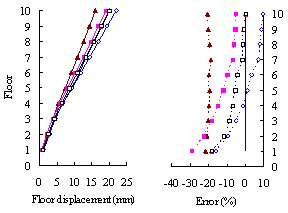
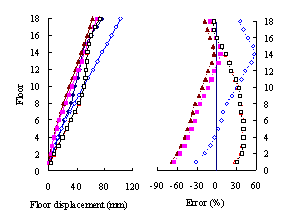
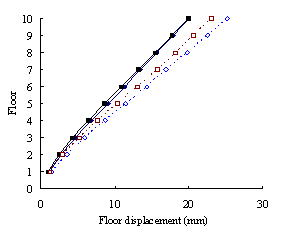
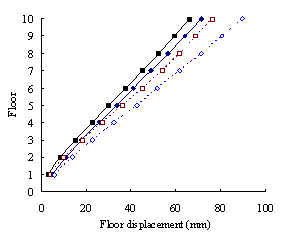
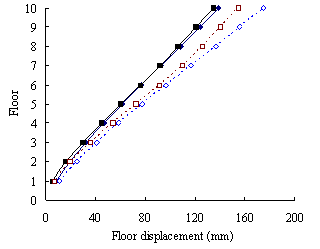
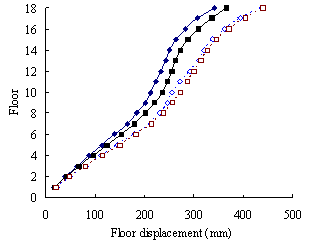
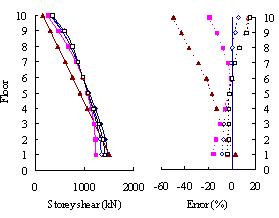
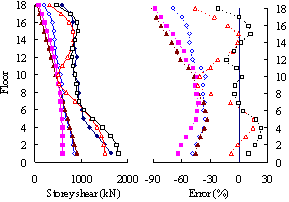
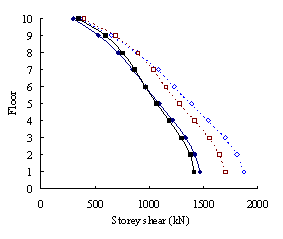
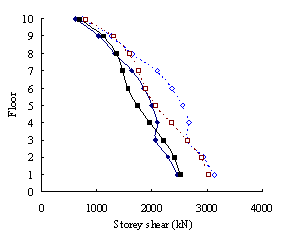
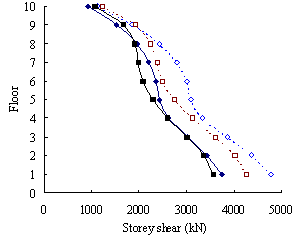
(2) For medium-rise frame-shear-wall structures, e.g. 10-storey, the pushover procedure with SRSS load pattern yields a sufficient accuracy in predicting the storey drift and storey shear. This is because the structure is not significantly influenced by the higher-order mode. The superiority of the MPA including higher-order modes for this type of structure is not apparent. Hence the SRSS pattern is ideal for medium-rise systems.

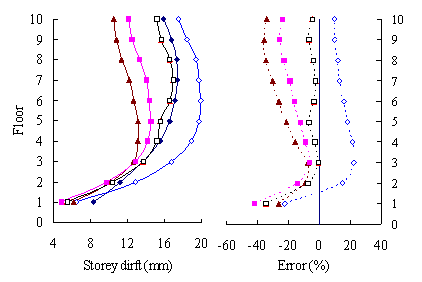
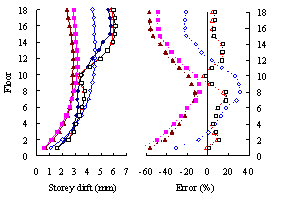
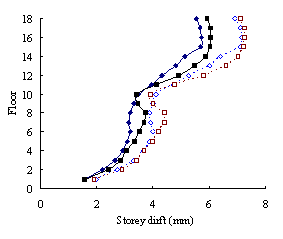
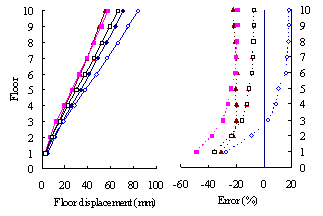
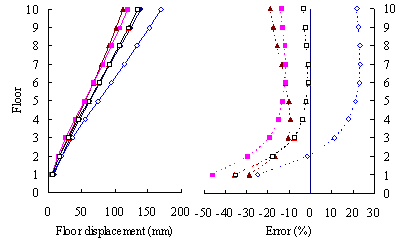
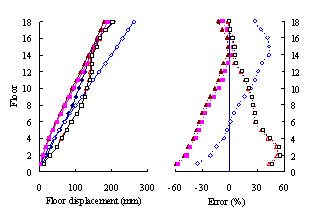
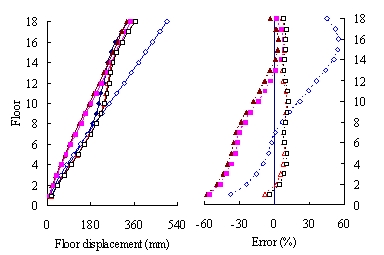
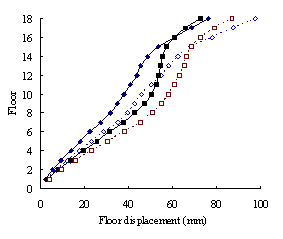
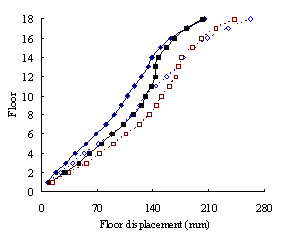
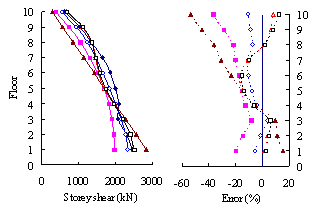
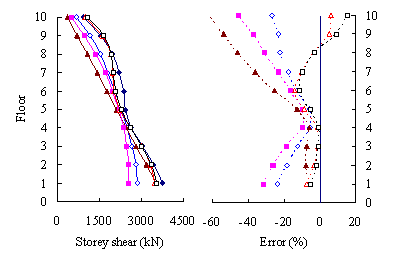
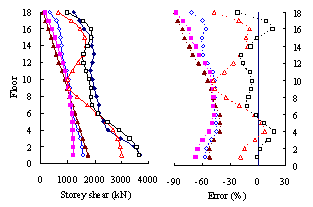
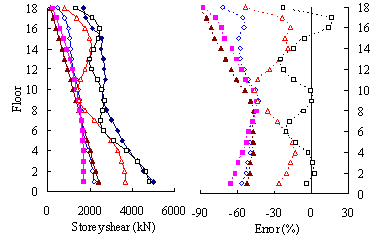
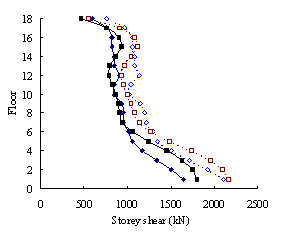
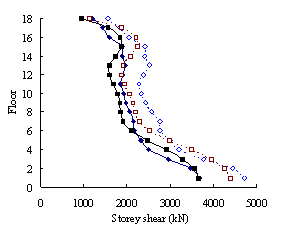
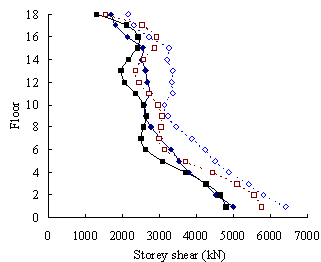
(3) For high-rise frame-shear-wall structures, e.g. 18-storey, the pushover procedures with invariant load patterns are unsuitable because significant contributions of higher-order modes to the structural responses are not taken into consideration. The MPA method including higher-order modes is superior to other pushover procedures. Such superiority is more remarkable in estimating structural responses for high-rise structures than the medium-rise counterparts especially for storey drift and storey shear.

(4) For both medium- and high-rise structures, the MPA method including higher-order modes is superior to other pushover procedures. Such superiority is more remarkable in estimating the peak storey drift and storey shear than the peak floor displacement.

Acknowledgement

The authors are grateful for the financial support received from the National Science Foundation of China (No. 90815025), Tsinghua University Research Funds (No. 2010THZ02-1) and ¡°Program for New Century Excellent Talents in University¡±.

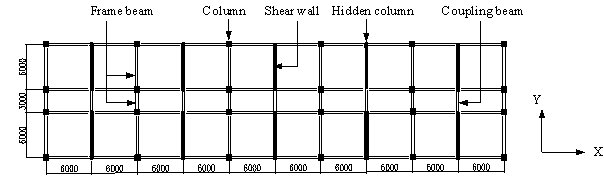
Appendix A: Analytical model

The planar system of frame-shear-wall structure (Figure 2) is modeled by the general purpose FEA software MSC.MARC (2005), which carries significant capacity of solving nonlinear problems.

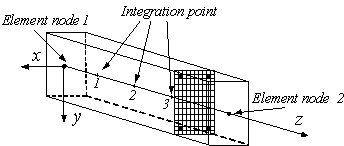
In this FEA model, RC frame members (RC beams and columns) are simulated by fiber-beam-element model together with one dimensional material constitutive law (Taucer et al. 1991). In the fiber-beam-element model, the beam section is divided into a number of fibers (Figure 3), the material property of which is described with uniaxial stress-strain relation, and the deformation among fibers follows plane section assumption. A program referred to as THUFIBER was developed by the authors and it is embedded into MSC.MARC (Ye et al. 2006). The number of concrete or reinforcement fibers can be so chosen according to the requirement of calculation.

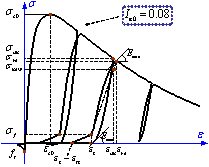
The stress-strain model proposed by L¨¦geron and Paultre (2003) is used in this work to model the backbone curve of concrete, which considers the confinement of stirrups to the concrete (Figure 18). Parabolic curves proposed by Mander et al. (1988) are adopted to model the unloading and reloading paths of concrete. This model takes into account the degradation of concrete strength and stiffness due to cycle loading. An exponential model proposed by Jiang et al. (2005) is used to model the softening branch of cracked concrete, with which the ¡°tension-stiffening effect¡± of reinforced concrete can be considered.

The stress-strain model proposed by Esmaeily and Xiao (2005) is adopted to model the backbone curve of steel (Figure 19). The model proposed by L¨¦geron et al. (2005) is adopted to model the unloading and reloading paths, in which the Bauschinger¡¯s effect of steel can be considered.

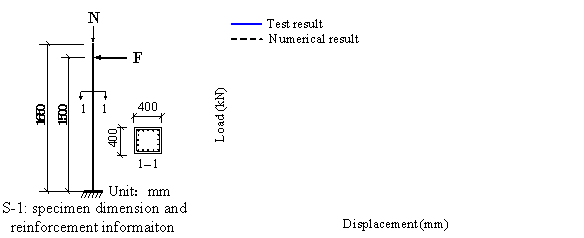
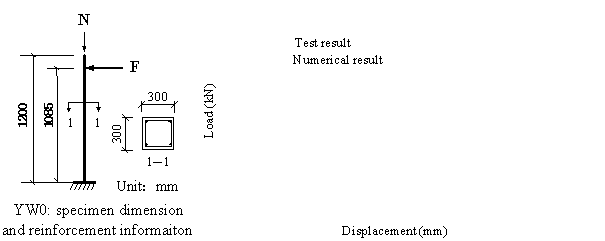
Two compressive-flexible RC column test specimens denoted as S-1 (Zatar et al. 2002) and YW0 (Li 2003) respectively, were simulated to verify the proposed fiber beam element model. S-1 has a larger reinforcement ratio (2.65%) and a smaller axial compressive ratio (0.03) whereas YW0 has a smaller reinforcement ratio (1.29%) and a larger axial compressive ratio (0.44). The simulation results agree well with the experiment . This can be demonstrated by the comparisons of load-displacement relation curves for S-1 and YW0, as shown in Figure 20 and Figure 21, respectively.

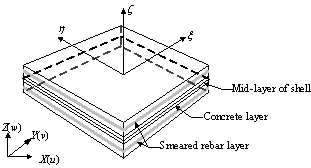
The shear-wall members (walls and coupling beams) in the FEA model are simulated by the multi-layer-shell-element (Figure 4). This element is based on the principles of composite material mechanics and can simulate the coupled in-plane/out-plane bending and the coupled in-plane bending-shear nonlinear behavior of RC shear walls (Miao et al. 2006). Basic principles of multi-layer-shell-element are illustrated by Figure 4. 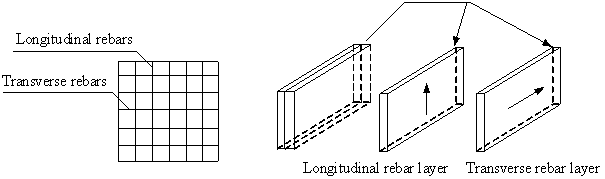The shell element is made up of a number of layers with different thicknesses and different material properties (Guan and Loo 1997). The rebars are smeared into one or more layers. The rebar layers can be either isotropic or orthotropic depending on the reinforcement ratio in the longitudinal and transverse directions, as shown in Figure 22. The elasto-plastic-fracture constitutive models provided by MSC.MARC and the steel model in Figure 19 (Wang 2007) are applied to the concrete and rebar materials, respectively. Since the multi-layer-shell-element directly relates the nonlinear behavior of the shear wall to the constitutive laws of concrete and steel, it has many advantages over other models in representing the complicated nonlinear behavior (Jiang et al. 2005).

Two shear wall test specimens denoted as SW2 (Chen 2002) and SJ-1 (Li 2005), respectively, were simulated to validate the shear wall model based on the multi-layer-shell-element. SW2 has a larger shear-span ratio (1.9) whereas SJ-1 has a smaller one (1.0). The dimensions and relevant reinforcement details of the specimens are shown in Figure 23 and Figure 24, respectively. Other information can be found elsewhere (Chen 2002, Li 2005). For specimen SW2, the experimental and numerical load-displacement curves are compared in Figure 23 and a good agreement is achieved. Similar conclusion can be drawn from Figure 24, which shows the load-displacement comparison for specimen SJ-1.

References

Albanesi, T., Nuti, C. and Vanzi, I. (2000). ¡°A simplified procedure to assess the seismic response of non-linear structures¡±, Earthquake Spectra, Vol. 16, No. 4, pp. 715¨C734.

ATC (1996). Seismic evaluation and retrofit of concrete buildings. Report ATC-40, Applied Technology Council, Red Wood City, Califonia, USA.

Bracci, J.M., Kunnath, S.K. and Reinhorn, A.M. (1997). ¡°Seismic performance and retrofit evaluation of reinforced concrete structures¡±, Journal of Structural Engineering (ASCE), Vol. 123, No. 1, pp. 3¨C10.

China Ministry of Construction. (2001). Code for seismic design of buildings (GB50011-2001), China Architecture & Building Press, Beijing.

Chintanapakdee, C. and Chopra, A.K. (2003). ¡° Evaluation of modal pushover analysis using generic frames¡±, Earthquake Engineering & Structural Dynamics, Vol. 32, No. 3, pp. 417¨C442.

Chopra, A.K. and Goel, R.K. (2002). ¡°A modal pushover analysis procedure for estimating seismic demands for buildings¡±, Earthquake Engineering & Structural Dynamics, Vol. 31, No. 3, pp. 561¨C582.

Chopra, A.K. and Goel, R.K. (2004). ¡°A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings¡±, Earthquake Engineering & Structural Dynamics, Vol. 33, No. 8, pp. 903¨C927.

Chou, C.C. and Uang, C.M. (2003). ¡°A procedure for evaluating seismic energy demand of framed structures¡±, Earthquake Engineering & Structural Dynamics, Vol. 32, No. 2, pp. 229-244.

Esmaeily, A. and Xiao, Y. (2005). ¡°Behavior of Reinforced Concrete Columns under Variable Axial Loads: Analysis¡±. ACI Structural Journal, Vol.102, No. 5, pp. 736-744

Fajfar, P. and Gaspersic, P. (1996). ¡°The N2 Method for the seismic damage analysis of RC buildings¡±, Earthquake Engineering & Structural Dynamics, Vol. 25, No. 1, pp. 31-46.

FEMA 273 (1997). NEHRP guidelines for the seismic rehabilitation of buildings, Federal Emergency Management Agency, Washington (DC), USA.

FEMA 274 (1997). NEHRP commentary on the guidelines for the seismic rehabilitation of buildings, Federal Emergency Management Agency, Washington (DC), USA.

FEMA 356 (2000). Prestandard and commentary for the seismic rehabilitation of buildings, Federal Emergency Management Agency, Washington (DC), USA.

Guan, H. and Loo, Y.C. (1997). "Layered Finite Element Method in Cracking and Failure Analysis of Beams and Beam-Column-Slab Connections". Structural Engineering and Mechanics - An International Journal, Vol. 5, No. 5, pp.645-662.

Gupta, A. and Krawinkler, H. (2000). ¡°Estimation of seismic drift demands for frame structures¡±, Earthquake Engineering & Structural Dynamics, Vol. 29, No. 9, pp. 1287¨C1305.

Han, S.W. and Chopra, A.K. (2006). ¡°Approximate incremental dynamic analysis using the modal pushover analysis procedure¡±, Earthquake Engineering & Structural Dynamics, Vol. 35, No. 15, pp. 1853¨C1873.

Jan, T.S., Liu, M.W. and Kao, Y.C. (2004). ¡°An upper-bound pushover analysis procedure for estimating the seismic demands of high-rise buildings¡±, Engineering Structures, Vol.26, No.1, pp.117-128.

Jiang, J.J., Lu, X.Z. and Ye, L.P. (2005). Finite element analysis of concrete structure. Tsinghua University Press, Beijing, China.(in Chinese)

Krawinkler, H. and Seneviratna, G.D.P.K. (1998). ¡°Pros and cons of a pushover analysis of seismic performance evaluation¡±, Engineering Structures, Vol. 20, No. 4, pp. 452¨C464.

L¨¦geron, F. and Paultre, P.(2003). ¡°Uniaxial confinement model for normal- and high-strength concrete columns¡±, Structure Engineering, Vol. 129, No. 2, pp. 241¨C252.

L¨¦geron, F., Paultre, P. and Mazar J. (2005). ¡°Damage mechanics modeling of nonlinear seismic behaviour of concrete structures¡±, Journal of Structural Engineering, ASCE, Vol. 131, No.6, pp. 946-954

Li, B. (2005). Nonlinear analysis of R/C frame-wall structures to multiple earthquake excitations and experimental research. PhD Thesis, Dalian University of Technology, Dalian, China. (in Chinese)

Li, J. (2003). Experimental investigation and theoretical analysis on seismic behavior of FS confined concrete columns. PhD Thesis, Tsinghua University, Beijing ,China. (in Chinese)

Mander, J.B., Priestley, M.J.N. and Park, R. (1988). ¡°Theoretical stress-strain model for confined concrete¡±. Journal of Structural Engineering, ASCE, Vol. 114, No. 8, pp.  1804-1826

Miao, Z.W., Lu, X.Z., Jiang, J.J. and Ye, L.P. (2006). ¡°Nonlinear FE Model for RC Shear Walls Based on Multi-layer Shell Element and Microplane Constitutive Model¡±, Proc. Computational Methods in Engineering And Science (EPMESC X), Tsinghua University Press & Springer-Verlag, Aug, Sanya, Hainan, China, CDROM

Moghadam, A.S. and Tso, W.K. (2000). ¡°Pushover analysis for asymmetric and set-back multi-story buildings¡±, Proceedings of the 12th World Conference on Earthquake Engineering, CD ROM. Auckland, New Zealand, February, Paper No. 1093.

MSC.Software Corp. (2005). MSC.Marc Volume B: Element Library.

Pacific Earthquake Engineering Research Center. PEER strong motion database [DB/OL]. California, Berkley. From URL: http://peer.berkeley.edu/smcat/index.html (September 2005).

Requena, M. and Ayala, G. (2000). ¡°Evaluation of a simplified method for the determination of the nonlinear seismic response of RC frames¡±, Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, February, Paper No. 2109.

Taucer, F.F., Spacone, E. and Filippou, F.C. (1991). ¡°A Fiber Beam-Column Element for Seismic Response Analysis of Reinforced Concrete Structures¡±, Report No. UCB/EERC-91/17, UC Berkeley, American.

Wang, X.L.(2007). Research on re-centering behavior of reinforced concrete column with unbonded high-strength strands. PhD Thesis, Tsinghua University, Beijing ,China. (in Chinese)

Ye, L.P., Lu, X.Z., Ma, Q.L., Wang, X.L. and Miao, Z.W. (2006). ¡°Seismic nonlinear analytical  models, methods and examples for concrete structures¡±, Engineering Mechanics, Vol. 23, No. (sup. II), pp. 131¨C140. (in Chinese)

Zatar, W. and Mutsuyoshi, H. (2002). ¡°Residual displacements of concrete bridge piers subjected to near field earthquakes¡±, ACI Structural Journal, Vol, 99, No. 6, pp. 740~749

List of Tables

Table 1.       Member dimensions and the reinforcement areas for 10-storey structure

Table 2.       Member dimensions and the reinforcement areas for 18-storey structure

Table 3.       Comparison between w_pi and w_i in distributed-mass model (DMM)

Table 4.       Comparison between w_pi and w_i in lumped-mass model (LMM)

Table 5.       Comparison of structural responses between DMM and LMM under earthquake No. 1

Table 6.       Comparison of structural responses between DMM and LMM under earthquake No. 2

Table 7.       Parameters of ten earthquake records

List of Figures

Figure 1.      Plan view of typical building storey (dimensions are in mm)

Figure 2.      FEA model of 18-storey structure

Figure 3.      Fiber-model element

Figure 4.      Multi-layer-shell-element

Figure 5.      Pseudo-acceleration spectrums of earthquake records and design spectrum in Chinese Code

Figure 6.      Peak storey drift for 10-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 7.      Peak storey drift for 18-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 8.      Statistical results of peak storey drift for 10-storey structure (THA and SRSS pattern)

Figure 9.      Statistical results of peak storey drift for 18-storey structure (THA and MPA-3modes)

Figure 10.    Peak floor displacement for 10-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 11.    Peak floor displacement for 18-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 12     Statistical results of peak storey drift for 10-storey structure (THA and SRSS pattern)

Figure 13.    Statistical results of peak storey drift for 18-storey structure (THA and MPA-3modes)

Figure 14.    Peak storey shear for 10-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 15.    Peak storey shear for 18-storey structure: (a) minor level; (b) moderate level; (c) major level

Figure 16     Statistical results of peak storey drift for 10-storey structure (THA and SRSS pattern)

Figure 17.    Statistical results of peak storey drift for 18-storey structure (THA and MPA-3modes)

Figure 18.  Concrete constitutive relation in THUFIBER

Figure 19.  Rebar constitutive relation in THUFIBER

Figure 20.  Numerical simulation for RC column specimen S-1

Figure 21.  Numerical simulation for RC column specimen YW0

Figure 22.  Location of rebar layers in multi-layer-shell-element

Figure 23.  Numerical simulation for shear wall specimen SW2

Figure 24.  Numerical simulation for shear wall specimen SJ-1

Table 1. Member dimensions and the reinforcement areas for 10-storey structure

Table 2. Member dimensions and reinforcement details for 18-storey structure

Figure 1. Plan view of typical building storey (dimensions are in mm)

Figure 2. FEA model of 18-storey structure

Figure 5. Pseudo-acceleration spectrums of earthquake records and design spectrum in Chinese Code

Figure 20. Numerical simulation for RC column specimen S-1

Figure 21. Numerical simulation for RC column specimen YW0

Figure 22. Location of rebar layers in multi-layer-shell-element

Figure 23. Numerical simulation for shear wall specimen SW2

Figure 24. Numerical simulation for shear wall specimen SJ-1