|
During collapse, impact and stack
load of fragments have a significant effect on the stories below, so
contact should be taken into account. There are three types of contact,
contact between finite elements, contact between discrete elements and contact
between finite elements and discrete elements. The first type of contact can
be directly set in finite element software MSC.MARC and the second and third
can be defined by user subroutine UBGITR. UBGITR will be called at the beginning
of each iteration.
(c) Effect of impact and stack loads.
When the discrete elements collide with finite element structure,
contact happens and user subroutine FORCDT will exert contact forces to the
nodes of relevant finite elements.
|

|

|

|

|
|
(a) t=0.0s
|
(b)
t=1.0s
|
(c)
t=2.0s
|
(d)
t=3.0s
|
Figure 2 Collapse procedure simulated with finite
element method (FEM)
|

|

|
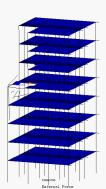
|

|
|
(a) t=0.0s
|
(b) t=1.0s
|
(c) t=2.0s
|
(d) t=3.0s
|
Figure 3 Collapse procedure simulated with coupled Finite element-discrete element method
A numerical example of an eight-story
frame is carried out to observe the effect of coupled finite element-discrete
element method. Columns and beams are modeled with fiber beam element model
and slabs with multi-layer shell element model. Progressive collapse occurred
after the corner column of the fifth story was removed. Two methods were applied
to simulate collapse, one is FEM and the other is coupled finite element-discrete
element method. The results from FEM are listed in figure 2 and those from coupled finite element-discrete element method (F/DEM)
are listed in figure 3. It is
noted that discrete elements can not be seen in Fig.11 because the program hasn’t support this function. At the beginning of collapse (before t=2.0s),
structural response of FEM is similar to that of F/DEM. When t=1.0s, the slabs
above the removed column break from the slabs around and drop off. When t=2.0s,
the fallen slabs crash through the fifth floor. However, these two methods appear
distinct results at 3.0s. With FEM, the progressive collapse is stopped after
the fourth floor slabs drop. With F/DEM, all the floor slabs below the removed
column are smashed. It is shown that the model based on F/DEM shows
a better simulation on impact and stack load in the process of progressive collapse
than that based on FEM.
5 Conclusions
Numerical simulation is an important tool to study
progressive collapse. Collapse of structure is a complicated process from continuum
into discrete bodies, which put forward requirements for the numerical model.
The model should not only simulate the nonlinear behaviors before collapse,
but also simulate impact and stack load of fragments during the collapse. Finite
element method has advantages in simulating continuum while discrete element
method in simulating the non-continuous behaviors after collapse
starts. Coupled finite element-discrete element method
(F/DEM) is proposed and implemented
based on existing finite element software. Keeping the advantages of FEM, the
method applies DEM to simulate the fragments in collapse. The numerical results
show that this coupled FEM-DEM method has a better simulation
on impact and stack load in progressive collapse than FEM.
Acknowledgements
This research is supported by National Science Foundation
of China (No. 50808106 & 90815025)
References
Xin-zheng Lu, Jian-jing Jiang (2001). Dynamic finite element simulation for the collapse of world trade center.
China Civil Engineering Journal,34(6), 8-11 [In Chinese].
Dong Qin, Li-chu Fan(2001). Numerical simulation
on collapse process of reinforced concrete structures. Journal of Tongji
University, 29(1), 80-83 [in Chinese].
Yu-zhu Cui, Chu-han Zhang,et al (2002). Numerical
modeling of dam-foundation failure and simulation of arch dam collapse. Shuili
Xuebao, 6,1-8 [in Chinese].
Li-ming Sun, Dong Qin, Li-chu Fan (2002).
A new model for collapse analysis of reinforced concrete. China Civil Engineering
Journal, 35(6), 53-58 [in Chinese].
D. Isobe, M. Tsuda(2003). Seismic collapse
analysis of reinforced concrete framed structures using the finite element method.
Earthquake Engineering and Structural Dynamics, 32, 2027-2046.
Gang Xuan, Xiang-lin Gu, Xi-lin Lü (2003). Numerical analysis
of collapse process for RC frame structures subjected to strong earthquakes.
Earthquake Engineering and Engineering Vibration, 23(6), 24-30 [in Chinese].
A. Munjiza, T. Bangash, N.W.M. John(2004).
The combined finite-discrete element method for structural failure and collapse.
Engineering Fracture Mechanics, 469-483.
Qiang Wang, Xi-lin Lü(2004). Application of the DEM to the seismic response analysis of
frame structures. Earthquake Engineering and Engineering Vibration, 24(5),
73-78 [in Chinese].
K. Khandelwal, and S. El-Tawil(2005). Multiscale
computational simulation of progressive collapse of steel frames. Proceedings of the ASCE Structures Congress, May 2005.
Ji-jun Miao, Xiang-lin Gu, et al (2005).
Numerical simulation analysis for the collapse response of masonry structures
under earthquakes. China Civil Engineering Journal, 38(9), 45-52 [in
Chinese].
Jun
Men, Xin-zheng Lu, et al (2006). Application of multi-layer model in shell
wall computation. Protective Structure 28:3,9~13 [in Chinese].
Jing-bo Liu, Yang-bing Liu, Jian-guo Yang
(2007). Simulation of earthquake ruins structure for the Earthquake Rescue Training
Base of China. Journal of Disaster Prevention and Mitigation Engineering,
27(suppl.), 428-432 [In Chinese].
Yan-chao Shi, Zhong-xian Li, Hong He(2007).
Numerical analysis of progressive collapse of reinforced concrete under blast
loading. Journal of PLA University of Science and Technology, 18(6),
652-658 [in Chinese].
Xin-zheng
Lu, Yan-sheng Zhang, Jian-jing Jiang (2007). Simulation for the collapse
of reinforced concrete frame by blasting based on fiber model. Blasting,
24(2), 1-6[in
Chinese]. Xun-liu
Wang, Xin-zheng Lu, Lie-ping Ye(2007). Numerical Simulation for the Hysteresis
Behavior of RC Columns under Cyclic Loads. Engineering Mechanics,
24(12),76-81 [in Chinese] [in Chinese].
Zhi-wei
Miao, Xin-zheng Lu, et al.(2007). Simulation for the collapse of RC frame
tall buildings under earthquake disaster. Computational Mechanics,
Proceedings of ISCM 2007, July 30
August 1, Beijing,China.
Feng-lei Zhao (2008). Simulation analysis
for collapse of reinforced concrete frame structures under earthquake based
on the discrete element method. Master thesis of Tongji University, Shanghai
[in Chinese].
Long-hai Wei, Chun-guang Chen, et al(2008).
Study on three-dimensional discrete element and parameter adoption. Journal
of Chongqing Jiaotong University (Natural Science), 27(4), 618-621,629.
Xin-zheng
Lu, Xu-chuan Lin,et al (2008). Numerical Simulation for the progressive
collapse of concrete building due to earthquake. The 14th World Conference
on Earthquake Engineering, Qctober 12-17, 2008, Beijing, China.
|