|
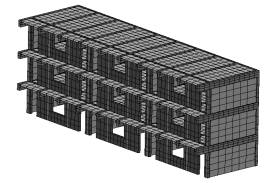
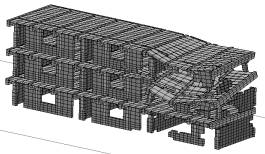
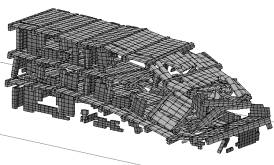
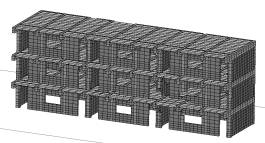
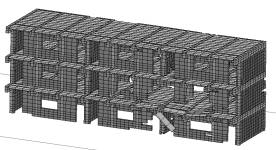
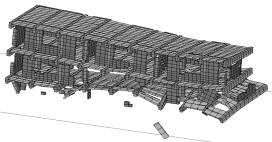
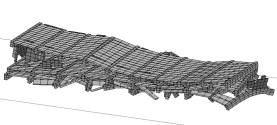
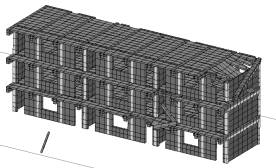
Case 4在Case 1基础上,增加了砖廊柱。2.5s时,结构一端的底部墙体丧失承载力,开始垮塌;0.7s后出现明显大面积垮塌,如图6。垮塌的特点是,失效的顺序是由下到上,结构沿长向梁端损伤更严重。由于砖廊柱的存在,结构大面垮塌的过程被延后。其原因是:一方面,砖廊柱可以分担少量走廊的竖向荷载,使梁下部墙体损坏的时间延后,一定程度上改善了结构的抗震性能;另一方面,廊柱对梁有一定的约束作用,可以减少因梁转动而引发的墙体开裂,但由于是砖柱,该作用有限。
|
|
|
|
(a) 2.5s
|
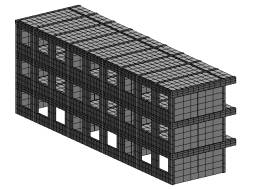
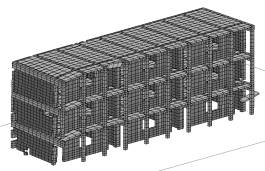
(b) 3.3s
|
|
图6 Case 4倒塌过程
|
3.5 地震动差异的影响
同一次地震,由于建筑离震源距离不同,场地条件不同,建筑朝向不同,结构受到的地震动作用也不同。Case 1、Case 5和Case 6输入的地震波形式分别为单向、双向和三向。Case
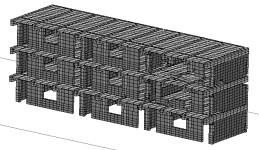
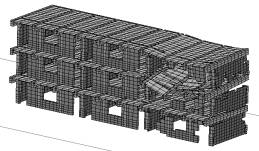
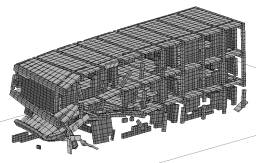
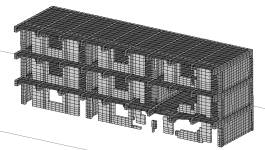
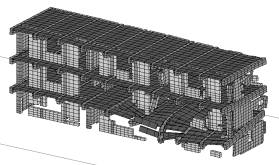
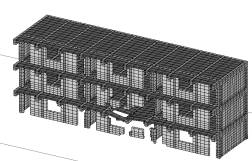
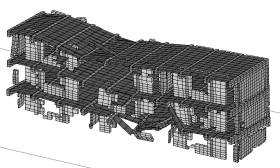
5在0.6s时底部两层右侧教室纵墙首先出现损伤,并导致墙体上方的几根梁塌落,如图7。Case 6首次出现破坏的的位置为底层纵墙中部,但后续破坏从三层的纵墙开始,如图8。而Case 1则在0.7s时在二层右侧教室出现损坏。
|
|
|
|
(a)0.6s(初始破坏)
|
(b) 0.9s
|
|
图7 Case 5在双向水平地震下的破坏形态
|
|
|
|
|
(a)0.4s(初始破坏)
|
(b) 0.9s
|
|
图8 Case 6在三向地震作用下的破坏形态
|
由于砌体墙体和预制楼板构成的结构,其整体性较差,在多向地震动作用下结构更容易垮塌,算例中三向地震作用下的Case 6出现明显局部垮塌的时间最早,而单向地震作用下的Case 1则最迟。可见,竖向地震动对砌体结构的影响比较明显,由于砌体强度一般较低,有时不能轻易忽略竖向地震动对结构的影响。
4 倒塌破坏模式及各措施比较
根据分析的算例,砌体结构在罕遇地震作用下主要有以下破坏模式:
1)连续垮塌模式:若未设置圈梁、构造柱,砌体结构的整体性较差,梁下部的承重纵墙首先出现损伤、垮塌,损伤的局部墙体将导致其他纵墙进一步损伤,梁失去足够的支撑而下落,预制板掉落,加上纵墙损伤的扩大,进一步导致周围的梁失去竖向或纵向支持,引发连续倒塌。尽管连续倒塌的模式沿着:承重墙→梁→预制板的方向进行,但是随着地震作用、材料强度、构造措施的不同,结构各个部分先后垮塌顺序各异,如逐层垮塌型(Case 2,4,6),单侧垮塌型(Case1、Case 4)等。一般情况下,结构边缘墙体破坏比中间墙体严重,底层墙体比上层严重,这与实际震害调查结果一致。
2)局部垮塌模式:结构具有较好整体性,墙体受到的作用力较均匀,仅出现预制板掉落或顶层边梁拉结失效而坠落的现象(Case 3)。一般情况下,悬挑走廊和结构两侧的预制板最易坠落。这种垮塌模式可以通过增强预制板的拉结来抵抗。
从以上算例可以看出,提高墙体的强度、设置圈梁和构造柱、设置廊柱等措施都可以提高砌体结构的抗震性能,但是各种措施的效果不同。显然,墙体的强度是一个很重要的因素,但砌体结构刚度大、变形能力小,在罕遇地震作用下,通过提高墙体强度是从提高承载力角度出发,一定程度延缓了结构倒塌,但无法提高结构整体性和变形能力。设置外廊柱,可以减小走廊一侧纵墙的压力,并对上部梁也有约束作用,从而延缓墙体局部出现损伤坍塌,但砖柱的碎散性导致这种功能有限。设置圈梁和构造柱是针对砌体结构整体性差的特点,加强结构的整体性(当然也提高承载力),从而显著提高结构抗震性能,这一措施是最有效的,本文算例及以往震害都说明了这一点。另外预制板端部可靠拉结对防止预制板坠落有重要影响。
5 结论与建议
1)基于有限元方法,本文提出了采用自体接触算法和生死单元方法模拟结构构件碎散、堆载过程,实现了砌体结构在罕遇地震下的倒塌全过程分析。
2)通过6个不同算例的分析,考查了材料强度、构造措施、廊柱等措施对结构抗震性能影响。提高墙体的强度、设置圈梁和构造柱、设置廊柱等措施都可以提高砌体结构的抗震性能,其中设置圈梁和构造柱的措施最为有效。
3)根据算例分析,砌体结构倒塌次序和破坏程度的不同,可以分为整体连续倒塌模式和局部倒塌模式。整体倒塌模式是由纵墙失效、坍塌引起的连续倒塌;局部倒塌主要是边梁或预制板的掉落。
4)砌体结构整体性相对较差,建筑离震源距离不同,场地条件不同,建筑朝向不同,结构的倒塌过程也明显不同,竖向地震对整体性较差结构的影响不可忽略。
5)本文的仿真表明,砌体结构应保证纵墙具有足够的强度储备,并设置必要的圈梁、构造柱,楼板需采取拉结措施,梁底部及门洞、窗洞角部应加强和进行构造处理。
参考文献
[1] Lynn, KM, Isobe, D. Structural
collapse analysis of framed structures
under impact loads using ASI-Gauss finite element method[J]. INTERNATIONAL
JOURNAL OF IMPACT ENGINEERING,34 (9): 1500-1516 SEP 2007
[2] Lynn, KMf. Finite
element code for impact collapse problems of framed structures[J].
INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING 69 (12): 2538-2563
MAR 19 2007
[3] Pekau, OA; Cui, Y. Progressive
collapse simulation of precast panel shear walls during earthquakes[J].
COMPUTERS & STRUCTURES, 84 (5-6): 400-412 JAN 2006.
[3] Khandelwal, K. and El-Tawil, S., Multiscale Computational
Simulation of Progressive Collapse of Steel Frames, Proceedings of the ASCE
Structures Congress, May 2005, NY, NY.
[4] Kaewkulchai, G., and Williamson, E.B., Beam
element formulation and solution procedure for dynamic progressive collapse
analysis, Computers & Structures, Vol. 82, 639-651.
[5] Isobe, D., and Tsuda, M.. Seismic
collapse analysis of reinforced concrete framed structures using the finite
element method[J], Earthquake Engineering and Structural Dynamics,
Vol.32, No.13, 2027-2046.
[6] XUAN Gang; GU Xiang-lin; LU·· Xi-lin. Numerical analysis
of collapse process for RC frame structures subjected to strong earthquakes[J].
Earthquake Engineering and Engineering Vibration,2003,23(06):24-30. (in Chinese)
[7] Lu Xinzheng Jiang Jianjing.
Dynamic finite element simulation for the collapse of world trade center[J].
China Civil Engineering Journal.2001,34(6):8-11. (in Chinese)
[8] Dorn, M. Computer
prediction of the damage to and collapse of complex masonry structures
from explosions[J]. .STRUCTURES UNDER SHOCK AND IMPACT, VI 8: 277-286
2000
[9] Yutaka Toi, Daigoro Isobe.TI: Adaptively
shifted integration technique for finite element collapse analysis of
framed structures[J]. International Journal for Numerical Methods
in Engineering.1999, Vol:36(14): 2323-2339. (in Chinese)
|