出屋面结构震害分析与设计建议

1  引言

在高层建筑中，经常有屋顶局部突出结构，如楼梯间、电梯间、水箱间、设备间和其它设施等，有时也有突出屋顶的构筑物或装饰结构。国内外多次大地震震害表明，屋顶局部突出结构的震害普遍严重。在遭遇强烈地震时，可能主体结构尚未破坏或损伤很轻，而突出物却发生严重破坏甚至倒塌。顶部突出结构的地震反应明增大的现象称之为“鞭梢效应”^{[1] [2]} 。在本次汶川大地震中，也发现大量出屋面局部突出结构由于“鞭梢效应”而受到严重损坏（图1~4）。这些出屋面结构破坏，会造成严重的心理恐慌（如绵阳商场因出屋面结构破坏而被暂时定为“停止使用”，造成居民严重恐慌，见图2），影响主体结构使用（如绵阳财政大厦顶部两层因出屋面结构破坏而不能使用，见图3），还可能造成结构物的连续破坏（安县秀水镇广电楼，出屋面发射塔倒塌后，将西侧两个开间从屋顶到底层砸穿，造成三人死亡，见图4），导致严重人员财产损失。

屋面突出结构“鞭梢效应”破坏的原因是该部分结构相对于下部主体结构有明显的刚度突变，而在地震作用下，建筑物顶部受高阶振动影响，地震反应较大，造成屋面突出结构产生很大的受力集中混入变形集中，极易造成较大的震害。由于目前因为建筑造型或设备功能需求，屋面突出结构仍有大量存在，所以有必要对其抗震设计方法进行更深入的研究，尽量减少“鞭梢效应”引起的严重震害。

本文利用有限元分析工具，以本次震害调查的某建筑物顶部突出结构参照，建立了一个典型的顶部具有突出屋面结构的高层建筑模型，并进行了弹塑性动力时程分析。通过模拟该建筑在实际地震作用下的弹塑性反应，分析了突出屋面结构的“鞭梢效应”震害，并结合目前的设计方法进行了探讨，对突出屋面结构的设计提出了建议。

2  现行设计中对突出屋面结构的处理

在现行抗震规范^[3] 中，对于突出屋面结构的设计计算的规定为：“在第一阶段按小震弹性阶段进行结构设计时，对于采用底部剪力法设计的结构，突出屋面部分的地震效应乘以增大系数3；而采用振型分解法计算时，突出屋面部分作为整个结构体系中的一个质点，参与整体结构分析，并按照多阶振型组合后的结果进行设计计算。”此外，在抗震规范中，虽然规定了对于部分特殊结构，应进行罕遇地震作用下的弹塑性变形验算，以检验是否达到了大震不倒的目标。如果大震作用下的层间变形超过限值，则应修改结构设计，直到层间变形满足要求为止。但是，对于主体结构规则且高度不超过规范限值，但顶层存在局部突出结构的情况，抗震规范没有明确规定对局部突出结构必须进行弹塑性变形验算。事实上，本次地震的震害表明，由于中震和大震水平下，屋面局部突出结构由于“鞭稍效应”会产生较为严重的震害。但现行设计规范中，只是在第一阶段设计过程中（小震）通过近似放大地震效应的措施来保证突出屋面结构不会由于鞭梢效应而发生严重破坏，却不能充分保证在中震和大震作用下，突出屋面结构能够满足弹塑性变形限值要求，避免严重破坏和倒塌。

3  本文分析模型和计算工具

为了研究在实际大震作用下，具有突出屋面结构的震害情况，本文利用有限元分析工具，建立了一个典型的顶部具有突出屋面结构的高层建筑模型，进行了弹塑性动力时程分析，模拟建筑在实际地震作用下突出屋面结构由于“鞭梢效应”而产生的震害。

首先利用工程设计软件PKPM设计了一个钢筋混凝土框架-核心筒高层结构，总高度为63.2m。其中下部结构15层，底层为4.8m，其它各层均为3.6m，顶部突出屋面结构为一个框架支承的2层小塔楼，高度为8m。抗震设防烈度为7度，场地类别为II类场地，设计地震分组为第一组，外框架和核心筒的抗震等级均为二级。筒体墙肢1-7层厚度为400mm，8-15层厚度为350mm，连梁、外框架柱、外框架梁的截面尺寸沿结构全高度分别为400mm×800mm、700mm×700mm、300mm×700mm，突出屋面结构的框架柱截面尺寸为400mm×400mm，高度为3.6m。

图5  结构三维空间有限元分析模型

由于本结构总高度较高，不满足采用底部剪力法的条件，因此设计计算时采用振型分解反应谱法，并将突出屋面部分作为整个结构中的一个质点，参与整体结构分析，取前15阶振型进行计算。根据PKPM的设计结果，提取各构件的配筋信息，然后在通用有限元分析软件MSC.Marc中建立结构三维空间弹塑性分析模型。结构外框架钢筋混凝土梁、柱和顶部突出结构的框架柱均采用清华大学土木工程系以MSC.Marc为平台所开发的纤维杆模型THUFIBER程序^[4] 进行分析，结构内部的核心筒剪力墙以及墙肢之间的连梁则采用清华大学土木工程系基于MSC.Marc所开发的分层壳单元模型^[5] 来模拟，并且其中墙体暗柱和连梁等关键部位的配筋采用离散钢筋模型。此外，楼板采用弹性壳单元来模拟，以考虑楼板变形的影响。在文献[4] [5] 中，对于以上所采用模型进行了详细的算例验证，表明这些分析模型可以将构件的宏观力学行为（节点力、节点弯矩）与材料的微观力学行为（应力、应变）直接联系起来，并通过选择合理的符合实际受力特点的材料本构模型，准确的模拟各构件的受力变形行为，因而可以较好的应用于结构的非线性数值模拟中。本文所建立的结构有限元分析模型如图5所示。

首先对结构进行了模态分析，得到结构的一阶模态为Y方向的平动，T₁=1.13s；二阶模态为X方向平动，T₂=1.12s；三阶模态为平面扭转振动，T₃=0.96s。

4  分析结果和讨论

首先对结构施加重力荷载代表值，由于本文结构在Y方向和X方向上完全对称，而顶部突出屋面结构在Y方向上的刚度小于X方向的刚度，因此本文主要研究在Y方向上输入地震动时程后的结构反应。本文挑选了EL-Centro EW和EL-Centro NS地震波作为输入地震动进行动力时程分析，为了考察结构在不同强度地震作用下的抗震性能，将地震峰值加速度PGA分别按《抗震规范》7度小震、中震、大震水准设置为35gal、100gal和200gal。

4.1 小震弹塑性时程结果

弹塑性时程分析结果表明，在小震水准作用下，主体结构均保持弹性，未产生破坏，顶部突出结构也未破坏，该层最大层间位移角分别为1/900和1/700，均小于规范对小震下钢筋混凝土框架弹塑性层间位移角的限值（1/550）。这说明，按照现行规范进行第一阶段设计后的结构，能够实现“小震不坏”的设计目标，顶部突出屋面结构也不会由于“鞭梢效应”而破坏。

4.2 中震弹塑性时程结果

弹塑性时程分析结果表明，在中震水准作用下，主体结构中除了连梁和底部筒体剪力墙开裂外，其它构件均保持弹性，没有构件发生屈服现象；同时，在EL-Centro EW地震波作用下，顶部突出结构未破坏，其中的框架柱保持弹性，该层最大层间位移角为1/300，而在EL-Centro NS地震波作用下，顶部突出结构中的框架柱出现塑性铰，但塑性程度不大，该层最大弹塑性层间位移角为1/146。这说明，按照现行规范，经过第一阶段设计后的结构在中震下基本可以实现“中震可修”的设计目标，顶部突出屋面结构的“鞭梢效应”震害要高于整个结构的平均震害。

4.3 大震弹塑性时程结果

弹塑性时程分析结果表明，在大震水准作用下，主体结构中连梁部分发生屈服，筒体剪力墙开裂严重，其它构件仍保持弹性；而顶部突出结构则发生严重破坏，其框架柱出现塑性铰，且进入塑性程度较大（受拉钢筋最大应变分别达到0.007和0.012，混凝土受压最大应变分别达到0.002和0.003）。图6显示了各构件的塑性铰分布状况，其中杆件端部深色表明该杆件出现塑性铰。

图7给出了这两条地震波大震水准作用下各楼层的最大层间位移角分布，显然，突出屋面结构层（第16层）层间变形集中。在EL Centro EW地震波作用下，突出屋面结构层最大弹塑性层间位移角为1/60，而在EL Centro NS地震波作用下，突出屋面结构层最大弹塑性层间位移角达到为1/42，超过了规范对于罕遇地震下钢筋混凝土框架弹塑性层间位移角的限值（1/50）。

4.4 结果分析及建议变形增大系数

由以上分析结果可见，对于本结构，虽然完全按照规范要求进行设计计算，但是仍无法避免屋面突出结构在强震作用下因“鞭梢效应”而受到严重损坏，产生较大弹塑性层间位移，难以实现“大震不倒”的目标。因此，在今后抗震设计中，对于此类突出屋面结构，应增加对弹塑性层间位移角的验算，如果大震作用下的层间变形超过限值，则应修改结构设计，增加出屋面结构的刚度或者配筋，直到其层间变形满足要求为止。

由于在工程设计中直接采用动力弹塑性时程分析代价较大，对工程师要求较高，因此为便于计算大震下屋面突出结构的弹塑性层间位移，可以参照现有规范中对于结构在罕遇地震作用下薄弱层（部位）弹塑性层间位移的简化计算方法，通过一定的弹塑性层间位移增大系数h_p来计算弹塑性层间位移。本文以前面得到的模型为基础，保持主体结构不变而仅增大突出屋面结构中框架柱的配筋A_s，从而提高该层的实际抗剪承载力和楼层屈服强度系数x_y，并且通过弹塑性时程分析计算了大震作用下突出屋面结构具有不同x_y时所对应的弹塑性层间位移增大系数h_p。表1中列出了相应的计算结果，其中，第一栏中A_s=1200mm²即为PKPM按照现行规范进行小震弹性设计得到的配筋结果。图8显示了大震作用下本模型x_y和h_p的关系（h_p取两条地震波计算结果的平均值）。

表1 大震作用下突出屋面结构层不同x_y时所对应的弹塑性层间位移增大系数h_p

注：A_s：框架柱实际配筋面积；

V_y：按照构件实际配筋和材料强度标准值计算的突出屋面结构层实际受剪承载力；

V_e：按照大震作用标准值计算的突出屋面结构层弹性地震剪力；

x_y：楼层屈服强度系数，x_y= V_y / V_e；

q_e：按照大震作用标准值，采用振型分解反应谱计算得到的突出屋面结构层弹性层间位移角；  

q_p：采用弹塑性动力时程分析方法得到的突出屋面结构层最大弹塑性层间位移角；

h_p：弹塑性层间位移增大系数，h_p=q_p / q_{e 。}

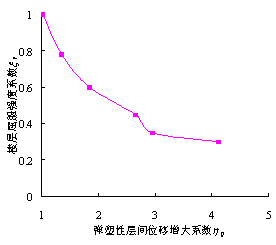
图8  大震作用下本结构模型x_y和h_p的关系

4.5 对现行设计方法的分析和讨论

由表1及图8可知，对于突出屋面结构层，当其框架柱配筋采用PKPM按照现行规范进行小震弹性设计得到的结果（A_s=1200 mm²）时，楼层屈服强度系数x_y仅为0.3，此时所对应的h_p可以达到4左右，该层的层间弹塑性位移很有可能超过规范对于罕遇地震下钢筋混凝土框架弹塑性层间位移角的限值（1/50），而当x_y增大时，h_p减小较为明显。这表明，现行设计方法中对屋面突出部分鞭梢效应的影响考虑仍然不够充分，将突出屋面部分作为整个结构体系中的一个质点，采用振型分解反应谱法取多阶振型进行组合，仍可能不能有效的保证大震下屋面突出结构不会发生严重损坏。因此，建议在屋面突出结构的抗震设计中，增加对弹塑性层间位移角的验算，并适当提高屋面突出结构的楼层屈服强度系数。

5  结论和建议

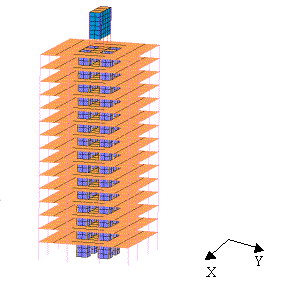
本文利用有限元分析工具，建立了一个典型的屋面顶部有突出结构的高层建筑模型，并进行了弹塑性动力时程分析，研究了突出屋面结构的“鞭梢效应”震害，并结合现行的相应设计方法进行了讨论，得到如下结论：

1）    按照现行抗震规范设计的具有突出屋面部分的结构，在对应于小震和中震水准的地震作用下，主体结构各构件基本保持弹性，顶部突出屋面结构的“鞭梢效应”震害也并不严重。

2）    按照现行抗震规范设计的具有突出屋面部分的结构，在对应大震水准地震作用下，顶部屋面突出结构的“鞭梢效应”震害较为严重，其最大弹塑性层间位移角有可能会超过规范相应的限制要求，突出屋面结构有可能发生严重震害和倒塌。因此，现行抗震规范针对突出屋面结构的设计规定不能有效控制大震下“鞭梢效应”的震害。

3）    为了防止屋面突出结构在大震作用下的严重震害，本文建议在设计中增加对突出屋面结构层的弹塑性层间位移验算。具体计算时，可以参照现有规范中对于结构在罕遇地震作用下薄弱层（部位）弹塑性层间位移的简化计算方法，通过弹塑性层间位移增大系数h_p来计算弹塑性层间位移。本文通过弹塑性动力时程分析，统计了突出屋面结构具有不同楼层屈服强度系数x_y时所对应的弹塑性层间位移增大系数h_p，但由于本文的研究只是针对一个结构模型，并且只计算了两条常用地震动记录下的反应结果，今后还需要进行更为系统的计算分析研究。

4）    由于屋面突出结构在整个建筑中所占比例很小，考虑到“鞭梢效应”可能导致的严重震害，适当增加屋面突出结构的抗震能力，其增加的费用有限，这对减少用户对地震的恐惧心理，震后尽快恢复建筑使用功能具有意义，也符合性能化抗震设计的理念的发展。

致谢：

本文感谢清华大学“数字防灾与虚拟工程”实验室提供高性能计算环境。

参考文献

[1]      李桂青, 熊火清, 结构鞭梢效应的控制与分析，地震工程与工程振动，1987,7(4): 1-14

[2]      杨佑发, 袁政强, 敬登虎, 高层建筑结构抗震设计中鞭梢效应的分析[J], 世界地震工程,2004, 20(1): 85-89

[3]      GB50011-2001，建筑抗震设计规范[S]，中国建筑工业出版社，北京，2002

[4]      叶列平, 陆新征,  马千里, 汪训流,  缪志伟, 混凝土结构抗震非线性分析模型、方法及算例[J], 工程力学, 2006, 23(Sup. ): 173-183

[5]      缪志伟, 陆新征, 叶列平, 分层壳单元在剪力墙结构有限元计算中的应用[J], 建筑结构学报, 2006, 27(Sup. 2): 932-935.