4
Implementation and Validation
The parallelization of the program is
achieved with the following steps:
(1) Program
the kernel function for the dynamic computing of a single building using CUDA
C.
Because every building is treated as an independent parallel
task, the entire time-history computing should run inside of one kernel
function. The kernel function¡¯s process should be as
follows:
a) Read the data of the single building assigned to this thread
from the global memory;
b) Perform the time-history computation;
c) Write the results to the global memory.
(2) Program
the host functions (running on the CPU), such as data inputting, copying and
outputting.
(3) Program
the main function, which manages the GPU resource and calls the kernel function
for computing.
To benchmark the performance of the parallelization
and the corresponding parameters,
the performance comparison between the GPU and CPU platforms is shown below.
4.2.1
Data for the benchmark
(1) 1 000 six-story buildings with the same parameters.
(2) Computational
time and steps: 40 s, 8 000
steps.
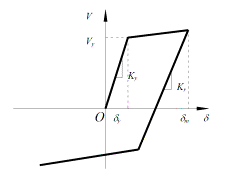
(3) Interstory
hysteretic model: bilinear hysteretic model (Figure 3).
(4) Only output
the result of 1 building to reduce the bottleneck effect caused by the hard
disk¡¯s writing speed.
4.2.2
Platforms
CPU£º
Intel Core i3 CPU 530 @2.93GHz
Memory£º
DDR3 4G 1333MHz
GPU £º NVIDIA GeForce GTX 460
Graphic memory: GDDR5 1GB 950MHz
The two platforms have similar prices (approximately 200 US
Dollars), so they can be used to compare their performance-to-price ratio.
In the test, the parallel computing
parameters of the program are as follows: grid=1, block=4, GPU_ Architecture=sm_10 (NVIDIA 2011).
4.2.3
Results of the benchmark
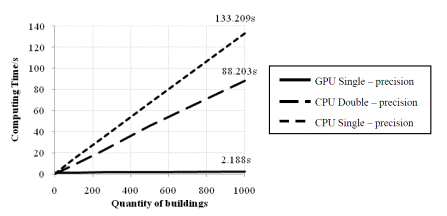
The relationship between the quantity
of buildings and computational time was compared, and the results are shown
in Figure 5.
Figure 5. Relationship between the quantity
of buildings and the GPU and CPU computing times
The computing time of the GPU is much shorter than that of
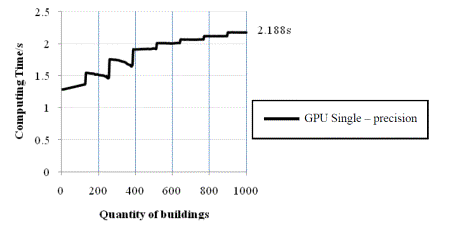
the CPU. Because the shape of the GPU computing time curve is unclear in Figure
5, it is enlarged in Figure 6.
Figure 6. Relationship between the quantity
of buildings and the GPU computing time
As Figures 5 and 6 show, the shape of the CPU program has
a linear time curve, indicating that the computing time is proportional to the
quantity of buildings. This result is consistent with the serial computing theory,
the concept of which is ¡°Single thread, Single task¡±. In contrast, the shape
of the GPU program¡¯s time curve is polyline, and the turning points are always
at the points at which the quantity of buildings is a multiple of 128 because
when using CUDA for parallel computing, every 32 threads in a same block constitute
a ¡°warp¡±. Inside of a warp, the parallel performance is very high, but there
is latency between two warps. In this test, the number of blocks is 4. Therefore,
when the number of threads is larger than 4¡°32=128, there will be one more warp to compute. Thus,
the computing time will elongate due to the scheduling latency. However, this
effect will be reduced as the quantity of threads increases. When the number
of threads is smaller than 384, the effect is very obvious; however, when the
number of threads is larger than 384, the effect is not as obvious because when
the quantity of threads is very large, CUDA can optimize the schedule of the
threads; thus, the latency is hidden in the computing time.
Comparing the GPU and CPU computing times shows that the GPU
is perfect for extensive parallel nonlinear time-history computing, as shown
in Figure 7.
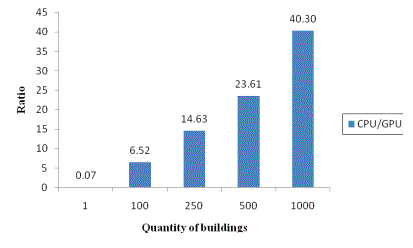
Figure 7. Comparison of the CPU/GPU
computing time ratio
When a single building is computed, the CPU computing time
is 7% of the GPU computing time because the performance of a single CPU core
is much better than that of a single GPU core. However, as the number of buildings
increases, the CPU computing time increases significantly, while the GPU computer
time increases slightly due to the parallelization. Thus, when 1 000 buildings are computed, the GPU computing
time can be 1/40 of the CPU computing time.
Table 1 compares the CPU and GPU results. When t=40.000
s (i.e., the last time point), there is approximately 0.1% error between them. This accumulated error
is due to the difference of the CPU and GPU¡¯s floating point computing rules.
The error is in an acceptable range and can thus be ignored.
Table 1 Results of the computations using
a CPU and GPU (t=40.000 s)
|
Displacement
(10-2 m)
|
1F
|
2F
|
3F
|
4F
|
5F
|
6F
|
|
GPU
|
0.522 84
|
0.709 95
|
0.247 54
|
0.196 42
|
0.196 33
|
0.196 28
|
|
CPU
|
0.522 72
|
0.709 70
|
0.247 29
|
0.196 16
|
0.196 07
|
0.196 02
|
|
Deviation
|
0.02%
|
0.04%
|
0.10%
|
0.13%
|
0.13%
|
0.13%
|
|