1. Introduction

Many modern cities are transforming into more sophisticated and integrated infrastructure systems, which significantly increases the risk of earthquake-induced damages in these cities. For example, the 2008 Wenchuan earthquake in China [1, 2] and the 2011 Christchurch earthquake in New Zealand [3] have led to massive loss of life and property. The resulting significant social, psychological and economic consequences have promoted the research in urban seismic damage simulation for improving emergency preparedness and mitigating possible earthquake-induced losses of high seismic regions and populous modern cities.

Hazus and MAEviz are widely used platforms for urban seismic simulation [4-6]. Both of these platforms are based on building inventory data. An inherent shortcoming of these platforms is that, the absence of the 3D geometric features of the buildings limits high-fidelity modeling of the geometric related dynamic properties of these buildings. For example, the proportion of the inter-story flexural deformation and shear deformation varies with the height/width ratio of the building, which results in different vibration mode shapes and natural frequencies [7, 8]. In addition, a vertically irregular plan layout may cause displacement concentration on floors with abrupt stiffness change. Therefore, without a proper consideration of the 3D geometric related dynamic properties of buildings, the seismic damage predictions may not be accurate and reliable.

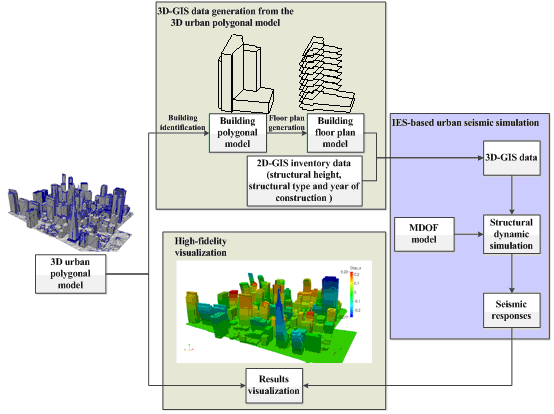
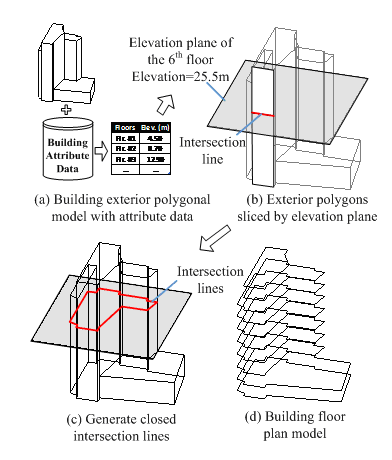
To better account for the dynamic properties in relation to the 3D geometric layout of buildings, Hori et al. [9] proposed the integrated earthquake simulation (IES) based on a 3D geographic information system (GIS). IES is able to perform the entire process of urban seismic simulation, including seismic ground motion generation, structural dynamic simulation and human/social response prediction. Accelerated by high-performance computing, IES has been adopted for the seismic simulation of Tokyo city [10]. In the simulation, 3D-GIS data are used as the input source, which contains all necessary geometric information (e.g., the floor plan on different elevations) and attribute information (e.g., structural height, structural type and year of construction) of buildings. Note that 3D-GIS data provide much more comprehensive information of buildings than the building inventory data. Note also that different computational models (e.g., multi-degree-of-freedom (MDOF) model and non-linear Distinct Element Method (DEM) [11]) are supported by IES thus making a full utilization of the available building information. Using the 3D-GIS data together with the IES-based urban seismic simulation can better predict the dynamic properties of individual buildings having irregular vertical and horizontal layouts.

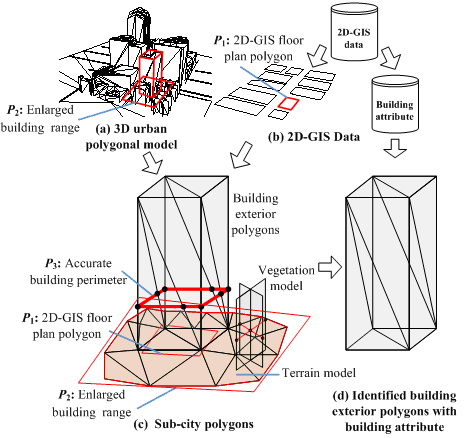
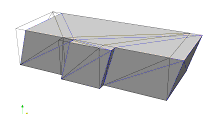
To date, however, limited 3D-GIS data can be utilized directly by IES. Due to security or confidentiality concerns, large amount of 3D-GIS data administrated by city governments or commercial companies are not publicly accessible. Even available, much of these 3D-GIS data adopt a 3D polygonal model or a solid model to represent the building geometric information [12, 13], which cannot provide the floor plan data that are required by IES. Furthermore, much of the available 3D-GIS data are in reality 2.5D data, which are extruded from the 2D-GIS plan layout polygons according to the building heights, as shown in Figure 1. Such 2.5D data cannot correctly represent the buildings that are vertically irregular. Thus, a methodology to generate the 3D-GIS data from the more accessible 3D city data is needed.

Figure 1. 2.5D data of Shantou, China

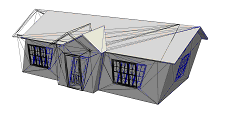
With rapid advances in light detection and ranging (LiDAR) together with photogrammetry technology [14, 15], 3D urban polygonal models of cities can be generated automatically or semi-automatically. Indeed, an increasing numbers of urban areas have accessible 3D urban polygonal models [16-19]. For example, Google provides global metropolises with realistic 3D models, as shown in Figure 2. Similarly, CyberCity3D provides 3D models for 62 cities in the United States (US) [19]. A 3D urban polygonal model contains comprehensive urban geometric information and has a wide range of applications in urban visualization and urban environment simulation (e.g., the application of city smoke propagation simulation [20]). In addition, high level of accuracy of the 3D urban polygonal model makes it viable to generate the 3D-GIS data [21]. For this reason, the 3D urban polygonal model is adopted in this study as the data source for the IES-based urban seismic simulation. Note that having two major differences from the 3D-GIS data required by IES, the 3D urban polygonal model (1) contains no descriptive information of each building (e.g., structural height, structural type and year of construction, etc.), such information is highly critical to estimate the dynamic properties of a structure; (2) is formed by building exterior polygons, whereas IES requires the floor plan as the input of the building geometric information, therefore, the 3D urban polygonal model cannot be used directly for the IES-based urban seismic simulation. In view of the limitations of the 3D urban polygonal model and given that the widely available urban 2D-GIS data can provide comprehensive building attribute information, a data conversion processes are thus proposed in this work to integrate the urban 2D-GIS data and the 3D urban polygonal model to generate the 3D-GIS data required for the IES-based urban building seismic simulation.

Figure 2. Google Earth 3D urban polygonal model

In addition to the structural dynamic simulation, the visualization of urban earthquake disaster scenario is also a very important component of any urban seismic simulation. A comprehensive visualization of urban building seismic responses can not only provide the government authorities and other stakeholders a better knowledge of the potential losses, but also offer a useful tool for disaster prevention training or disaster emergency preparedness planning [22-24].

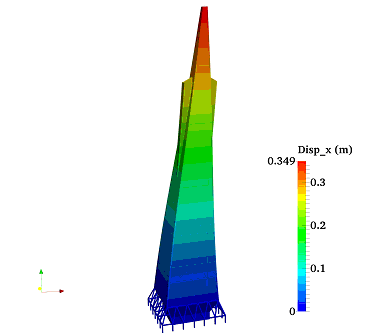
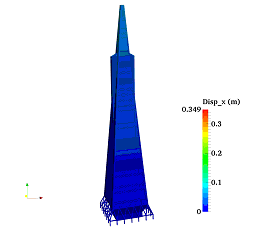
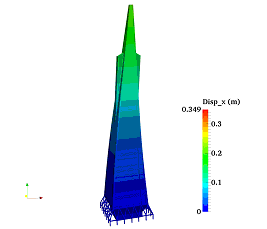
Despite of the calculation power of the IES-based urban seismic simulation, its computational models in general cannot be used directly to produce a high-fidelity visualization of the simulation. For example, when using the MDOF computational model, each building floor is represented by only a mass point, which is far from a realistic visualization. Conventionally, if the 3D-GIS data are not available, the 2.5D model that is generated by extruding the buildings from the floor plan polygons (Figure 1) will be used [25]. Obviously, such a 2.5D model is also far from the realistic façade. In addition, non-building objects, such as terrain, roads and vegetation, are neglected in the visualization. Hence, current seismic visualization methods have much room for improvement.

In contrast to the 2.5D model, the 3D urban polygonal model featured with rich architectural details can provide a realistic visualization for building as well as non-building objects. As a result, the 3D urban polygonal model is used herein to visualize the urban building seismic responses with high-fidelity of urban earthquake disaster scenario. In this work, deformations of buildings predicted by IES will be mapped to the 3D urban polygonal model to generate high-fidelity and realistic visualizations of the seismic response. In addition, both building and non-building objects of the original 3D urban polygonal model will be visualized to make the visualization more realistic.

2. Overview of the proposed methodology

The proposed methodology includes three components: (1) 3D-GIS data generation from the 3D urban polygonal model, (2) IES-based urban seismic simulation, and (3) high-fidelity visualization. The interconnection of the three components is illustrated in Figure 3.

Figure 3. Overview of proposed urban seismic simulation using 3D urban polygonal model

Component 1: 3D-GIS data generation from the 3D urban polygonal model

As described earlier, 3D-GIS data used by IES as building data input are not always accessible, whereas the accessibility of the 2D-GIS data and 3D urban polygonal model are much higher. Hence, in this component, the 2D-GIS data together with the 3D urban polygonal model are adopted to automatically generate the 3D-GIS data for an urban seismic simulation. This is accomplished in three steps: (1) the building exterior polygons are identified and filtered out from other non-building objects; (2) the identified building polygons are mapped with its corresponding building attribute data (e.g., structural height, structural type and year of construction) from the 2D-GIS data; (3) the floor plan generation method is conducted to acquire the floor plan polygons from the building exterior polygons. The 3D-GIS data will then be utilized by IES to generate computational models for subsequent seismic simulation.

Component 2: IES-based urban seismic simulation

Based on the 3D-GIS data, reliable computational models will be generated for the IES-based urban seismic simulation. According to the building attribute information, IES can use different computational models (e.g., the MDOF model and DEM [11]). Thus, dynamic responses of the structure due to its irregular horizontal or vertical layouts can be predicted by combining the 3D-GIS data and IES. The time-history analysis is performed in IES for each building. The seismic response results will subsequently be visualized using the proposed high-fidelity visualization method based on the 3D urban polygonal model.

Component 3: High-fidelity visualization

The 3D urban polygonal model, which provides a realistic urban scene, is used as the basis for the high-fidelity visualization. For each building, the seismic response results (e.g., displacement) from IES will be assigned to its corresponding exterior polygons so that the building objects in the 3D urban polygonal model can display the seismic response. In addition to the building objects, other urban objects, such as terrain, roads and vegetation, can also be visualized in the urban scene to improve the reality of the visualization.

Details of the 3D-GIS data generation method and the high-fidelity visualization method are presented in Section 3 and Section 4 of this work, respectively. The implementation of the IES-based urban seismic simulation is briefly introduced in Section 5.2. Given that the structural dynamic simulation is not the main focus of this work, details of IES can be found elsewhere in Hori et al. [9, 10].

3. 3D-GIS data generation

3.1 3D building model

Several different methods can be used to define a 3D model of a building (e.g., 3D polygonal model and solid model) [14]. Note that most existing 3D polygonal models possess the following characteristics: (1) they are widely adopted by the most influential 3D city platform, Google Earth [12], (2) they can be easily accessed from several commercial companies [18, 19] or free model warehouses [26, 27], (3) their accuracies (of a sub-meter level) are adequately high to generate desirable 3D-GIS data [21, 28]. For these reasons, the present work thus emphasizes how to generate 3D-GIS data based on a 3D polygonal model. A typical 3D urban polygonal model is shown in Figure 4(a). In addition to the building objects, the model also includes non-building objects, such as terrain and roads. In contrast, the 3D-GIS model required by IES (Figure 4(b)) contains only the building objects. To implement an automatic conversion from the 3D urban polygonal model to the 3D-GIS model, the following challenges must be tackled.

(1) Only building objects are required by the IES-based seismic simulation. Hence, they must be identified and non-building objects must be filtered out.

(2) The 3D urban polygonal model has no attribute data for buildings. Thus, additional building descriptive information must be read from the 2D-GIS data and mapped to the corresponding buildings.

(3) A conversion algorithm is required to generate the floor plan polygons from the building exterior polygons.

Figure 4. 3D model conversion

3.2 Building identification

The primary task of building identification is to acquire the exterior polygons of each individual building from the 3D urban polygonal model and assign the building attribute data to the acquired geometries thereby generating the 3D-GIS data. To achieve this, the 2D-GIS data containing the ground floor plan polygon of each building are used to identify the building objects. The exterior polygons of the building object in the 3D polygonal model can be identified if the polygons are located within the ground floor plan polygon of the 2D-GIS data. However, the floor plan polygon in the 2D-GIS data does not always entirely coincide with that of the 3D urban polygonal model. A special algorithm is thus proposed to extract exterior polygons of a building and match its 2D-GIS data with its 3D urban polygonal model. This refers to as the ¡°building identification¡±, as presented in Figure 5.

Figure 5. Building identification

The process of building identification begins from subdivision of the city polygons, i.e. dividing the original 3D urban polygons (see Figure 5(a)) into sub-cities each containing only one building (see Figure 5(c)). A 2D-GIS building floor plan polygon P₁ obtained from the 2D-GIS data (see Figure 5(b)) is gradually enlarged to polygon P₂ (see Figure 5(a)), ensuring that all of the corresponding building polygons in the 3D urban polygonal models are located within the range of P₂. All of the polygons located in P₂ are then extracted and named SubCityPolys (Figure 5(c)). The SubCityPolys contains not only building objects but also non-building objects like vegetation model and terrain model. To identify the building exterior polygons, all of the SubCityPolys are sliced at 0.5 m elevation from the ground level to obtain the building perimeter polygon P₃ (Figure 5(c)). The acquired polygon P₃ is then used to identify the exterior polygons of each individual building. All of the polygons of which the projections are located within P₃ are extracted as the building exterior polygons as shown in Figure 5(d).

Once the exterior polygons corresponding to the individual building in 2D-GIS database are extracted, the building attribute data available in the 2D-GIS database is then assigned to the identified exterior polygons to generate the 3D-GIS building data (Figure 5(d)).

3.3 Floor plan generation

The building identification process yields the 3D building exterior polygon models with attribute data, see Figure 5(d). Nevertheless, the floor plan polygons (Figure 6(d)) are required as the geometric input for IES. As such, the floor plan generation method is proposed to obtain the floor plan polygons for each building.

The procedure is illustrated in Figure 6. The 3D building exterior polygons together with the building attribute information are used as the input for the floor plan generation (see Figure 6(a)). The elevation of each floor is obtained from the building attribute data. The floor plan generation is subsequently implemented for each floor elevation. As an example shown in Figure 6(b), an exterior polygon of the building on the elevation of the 6^th floor is sliced, which generates an intersection line. The same process is repeated for all of the exterior polygons and a group of intersection lines is generated (see Figure 6(c)). These lines are connected to form a closed polygon, which represents the floor plan polygon of the 6^th floor. Following the same procedure for all the remaining floors yields the floor plan of each floor (see Figure 6(d)).

Figure 6. Floor plan generation

Through the above process, the 3D-GIS data containing the floor plan polygons and the building attribute information are obtained automatically and are suitable for the IES-based urban seismic simulation. The implementation of the urban seismic simulation is discussed in Section 5.2.

4. High-Fidelity Visualization

Through the urban seismic simulation of buildings, large amounts of building response results are generated. Realistically visualizing all these results still remains a significant challenge. In this study, the 3D urban polygonal model is used to achieve high-fidelity visualization of urban seismic simulation results.

4.1 Data preparation

To visualize the seismic behavior of the buildings using the realistic 3D urban polygonal model, the seismic response results must be assigned to each building. To achieve this, all polygons in the 3D urban polygonal model need to be classified into two groups: (1) the first group is BuildingPolys, which represents the exterior polygons of buildings and will deform according to the seismic response from IES. (2) The second group is NonBuildingPolys which is the polygons of terrain model, vegetation model and some other objects that are filtered out by the building identification method. NonBuildingPolys is helpful to improve the reality of urban scene. Therefore NonBuildingPolys is also utilized in high-fidelity visualization.

4.2 Model remeshing

Time-history analysis of IES generates seismic displacement results of buildings on different floors. However, as illustrated in Figure 7(a), the floor concept is not reflected in the original 3D building polygonal model. Therefore, remeshing needs to be performed to visualize different displacements on respective floors (Figure 7(b)).

To remesh the original 3D building polygonal model, the building attribute data are used to provide the elevation of each floor. Subsequently, every exterior polygon of the building is checked to determine whether it intersects any floor elevation plan: (1) if yes, the polygon is sliced on the floor elevation and is divided into a series of shorter polygons, each of which is located inside one floor only. These shorter polygons are then stored in their corresponding floor object. (2) if not, the polygon is stored in their corresponding floor object directly. As evident in Figure 7(a), many polygons stretch across more than one floor in the original model. Whereas in the remeshed model shown in Figure 7(b), the polygons are divided making all the shorter polygons to be located inside the corresponding floor.

Figure 7. Model remeshing for visualization

4.3 Interpolation of displacement

The computational model of IES only generates the seismic displacement results on a few discrete elevations. As an example shown in Figure 8(a), the MDOF model of IES only generates the displacement result d₁ on Elevation 1. The polygonal model of Figure 8(b) is used to visualize the displacement d₁. If d₁ is assigned only to the vertices of the 3D polygonal model on Elevation 1, the visualization effect is as shown in Figure 8(c), where all of the vertices between the two adjacent floors are disconnected from the floor displacement. This is obviously undesirable. Therefore, a linear interpolation of displacement is performed to ensure that all of the vertices between two adjacent floor elevations deform according to the overall building response. The coordinates of all the vertices are updated according to Equations (1) and (2). A more realistic visualization with displacement interpolation is achieved as demonstrated in Figure 8(d).

 (1)

 (2)

where: x_n,updated/y_n,updated and x_n,original/y_n,original are respectively the updated and original x/y-coordinates of the n^th node.  d_0,x/d_0,y and d_1,x/d_1,y are the computed seismic displacements of the lower adjacent elevation (e.g., Evaluation 0 in Figure 8) and the upper adjacent elevation (e.g., Evaluation 1 in Figure 8) of this node, respectively, in the x/y-direction. h_n is the distance between the n^th node and Evaluation 0. H is the floor height.

Figure 8. Displacement interpolation

5. Implementation

In this section, detailed data flow and tools of the entire data generation and visualization methodology are discussed.

5.1 Data flow

As illustrated in Figure 9 and Figure 3, the data generation method starts from the input data. The 3D urban polygonal model studied here is based on an open Extensible Markup Language (XML)-based 3D model format called Collaborative Design Activity (COLLADA) Digital Asset Exchange (DAE) [29]. An open sourced parser named TinyXML [30] is used to parse the 3D urban polygonal model. All the vertex coordinates and polygons from the DAE file will be stored in CityPolys.

Figure 9. Data flow diagram of the entire data generation and visualization methodology

In the first step of 3D-GIS data generation, CityPolys together with 2D-GIS data are utilized by CityPolys subdivision method to generate SubCityPolys for each building. Next, building identification is performed for each SubCityPolys and the identified building polygons are stored in Buildings[i].ExteriorPolys (see Figure 9), where i is the building index, while other polygons are stored in NonBuildingPolys for the purpose of further high-fidelity visualization. Subsequently, the attribute data of each building from 2D-GIS are stored in the corresponding Building object, named Buildings[i].Attribute. Finally, floor plan generation will be implemented using the elevation data from Buildings[i].Attribute and the geometry data from Buildings[i].ExteriorPolys; and the obtained floor plan results will be stored in Buildings[i].Floor[j].FloorPlan, where Floor[j] is used to store all data related to the j^th floor.

The data flow for high-fidelity visualization is as follows: the seismic response results obtained from the IES-based urban seismic simulation are stored in its corresponding Building object. Specifically, the time-history results for each floor are stored in the corresponding Buildings[i].Floor[j].Response. Subsequently, model remeshing procedure is performed and the polygons from Buildings[i].ExteriorPolys are divided into shorter polygons and stored in its corresponding floor named Buildings[i].Floor[j].RemeshedExteriorPolys.

5.2 Seismic analysis

IES is capable of determining the dynamic parameters of building numerical model, e.g., the mass, inter-story stiffness and inter-story strength, according to the plan of each floor [9, 11]. When the floor plan abruptly changes along the height, these quantities of the corresponding floor determined by IES will be significantly different from the adjacent floors, thereby resulting in displacement concentration due to the vertically irregular floor plan layout. Details of the parameters determination procedure can be found in the work of Hori [9], Sobhaninejad et al. [11] and Lu et al. [25].

After the dynamic parameters of each floor are determined, a suitable numerical model (e.g., the MDOF model in this study) can then be adopted by IES to perform a nonlinear time-history analysis. To avoid convergence problems, the central difference method [31] is adopted for the time-history analysis. The seismic responses on each floor of each building can then be acquired. These response results are useful for the subsequent high-fidelity visualization.

5.3 Visualization tool

As an open sourced visualization tool that supports various types of geometric objects, VTK [32] is used herein to visualize the urban seismic scenario. Moreover, VTK also supports user defined variables for geometric objects. All of these features make the VTK a suitable tool to visualize the simulation response results.

VTK is a post-visualization tool and also a 3D model file format. In this study, the urban polygonal model (i.e., Buildings[i].Floor[j].ExteriorPolys and NonBuildingPolys presented in Figure 9) together with the building seismic response results Buildings[i].Floor[j].Response (Figure 9) are converted to the VTK format and the VTK file is visualized using the Paraview software [33]. The VTK file format also follows the XML schema, the primary tree structure is shown in Figure 10. The Points element is used to store the coordinates and indices of points. The PointData element is for user defined variables on each point, for example, it can be used to store the point displacement or acceleration results. The Polys element is used to store the connectivity information and indices of polygons. The CellData element is for user defined variables of each polygon, for example, the damage state data on different floors.

Figure 10. XML tree for VTK file

6. Case studies

A 3D urban polygonal model containing 78 buildings is studied herein to demonstrate the proposed 3D-GIS generation method and high-fidelity visualization method. The corresponding 2D-GIS data of this 3D urban polygonal model include the number of floor, height, year of construction and structural type of each building. Typically selected examples of the 2D-GIS building inventory data are listed in Table 1.

6.1 Verification of the 3D-GIS data generation method

The 3D urban polygonal model just mentioned is used to validate the proposed building identification method. All of the 78 buildings are identified automatically, which demonstrates the robustness and capacity of the proposed method. Note that for some special cases if the automatic procedure fails to identify all the buildings, the IDs and positions of the unidentified buildings will be outputted according to 2D-GIS data. These unidentified buildings can be further checked and handled manually.

When implementing the floor plan generation, some small gaps between different building exterior polygons may exist. A gap tolerance, i.e. the ratio between the width of gap (i.e., dD) and the floor height (i.e., H), should be defined initially. If the gap between two intersection lines (see Figure 6) is smaller than the gap tolerance, the two lines are treated as being connected. The relationship between the percentage of successful floor plan generation and different gap tolerances is shown in Figure 11. It reveals that if the gap tolerance is greater than 2.5 % of the floor height, the percentage of successful generation of the floor plan reaches 100 %. Thus, this tolerance value is recommended in the analysis.

Figure 11. Relationship between the gap tolerance and the percentage of successful floor generation

6.2 Scalability of the 3D-GIS data generation method

There are a large number of buildings in a modern and populous city. The size of a 3D urban polygonal model is normally very large. As a result, it is essential to examine the scalability of the data generation, or the conversion method. This is performed by applying the method to models of different sizes. Note that the computer platform used in this study is a desktop computer with a 2.4-GHz Intel Core i3 M370 CPU, together with 4GB of 1333-MHz DDR3 RAM and NVIDIA NVS 3100M graphic card. The compiler adopted is Microsoft Visual C++ 2010.

The computational time required for different model sizes is displayed in Figure 12. The results show a closely linear scalability. This approximate linearity is a result of the proposed ¡°Citypolys subdivision¡± method which divides the entire 3D urban polygonal model into a series of much smaller models according to the perimeter of each individual building in the 2D-GIS data. Such linear scalability suggests that the proposed method is applicable to large-scale urban scenarios.

Figure 12. Scalability of the 3D-GIS data generation method

6.3 Realistic effect of high-fidelity visualization

To demonstrate the realistic effect of the high-fidelity visualization, the proposed method is compared with the conventional 2.5D visualization approach. As evident in Figure 13, the 2.5D models (Figure 13(a)) present much less details than the corresponding high-fidelity models (Figure 13(b)).

High-fidelity models can also be used to visualize time-history responses of buildings, an example of which is shown in Figure 14. The proposed method has the ability to output the displacement contours for different time steps, thus making it possible to generate an animation of the building seismic responses (see Figure 15).

Figure 14. Visualization of the seismic displacement of a building

Finally, the proposed high-fidelity visualization method is applied to visualize the earthquake disaster scenario of an area with 78 buildings. The results are displayed in Figure 16 where both buildings and non-building objects (e.g., the terrain) are clearly demonstrated in the visualization. Such is significantly more realistic than the outcome of 2.5D visualization, as presented in Figure 17.

Figure 16. An urban earthquake disaster scenario with high-fidelity visualization

Figure 17. An urban earthquake disaster scenario with 2.5D visualization

7. Conclusions

Using the existing 3D urban polygonal model, this work has proposed a 3D-GIS data generation method for the IES-based urban seismic simulation and a high-fidelity visualization method for displaying the simulated urban earthquake disaster scenario.

A building identification and floor plan generation method is proposed to automatically generate the 3D-GIS data for the IES-based urban seismic simulation based on the 3D urban polygonal model and the 2D-GIS data, which is widely accessible. The numerical example indicates a linear scalability of the proposed method, which enables the method to be used for large-scale urban scenarios.

Further, a remeshing and a displacement interpolation techniques is developed to display the seismic response results from IES for high-fidelity visualization. Overall, the proposed visualization method is proven to be significantly more realistic than the existing 2.5D visualization method. In addition, non-building objects can also be visualized in the same urban scene, which results in a more vivid urban earthquake disaster scenario.

Acknowledgements

The authors are grateful for the financial support received from the National Key Technology R&D Program (No. 2013BAJ08B02), the National Natural Science Foundation of China (No. 51222804£¬51178249£¬51378299).

References

[1] Z. Wang, A preliminary report on the Great Wenchuan Earthquake, Earthquake Engineering and Engineering Vibration 7(2) (2008) 225-234.

[2] X.Z. Lu, L.P. Ye, Y.H. Ma, D.Y. Tang, Lessons from the collapse of typical RC frames in Xuankou school during the Great Wenchuan Earthquake, Advances in Structural Engineering 15(1) (2012) 139-153.

[3] J.R. Stevenson, H. Kachali, Z. Whitman, E. Seville, J. Vargo, T. Wilson, Preliminary observations of the impacts the 22 February Christchurch Earthquake had on organizations and the economy a report from the field (22 February-22 March 2011), Bulletin of the New Zealand Society for Earthquake Engineering 44(2) (2011) 65-76.

[4] C.A. Kircher, R.V. Whitman, W.T. Holmes, Hazus earthquake loss estimation methods, Natural Hazards Review 7(2) (2006) 45-59.

[5] P.J. Schneider, B.A. Schauer, Hazus¡ªits development and its future, Natural Hazards Review 7(2) (2006) 40-44.

[6] A.S. Elnashai, S. Hampton, H. Karaman, J.S. Lee, T. Mclaren, J. Myers, et al., Overview and applications of MAEviz-Hazturk 2007, Journal of Earthquake Engineering 12(S2) (2008) 100-108.

[7] R.K. Goel, A.K. Chopra, Period formulas for concrete shear wall buildings, Journal of Structural Engineering 124(4) (1998) 426-433.

[8] Uniform building code, International Conference of Building Officials, Whittier, CA, USA 1997.

[9] M. Hori, Introduction to computational earthquake engineering, World Scientific 2011.

[10] T. Yamashita, M. Hori, K. Kajiwara, Petascale computation for earthquake engineering, Computing in Science & Engineering 13(4) (2011) 44-49.

[11] G. Sobhaninejad, M. Hori, T. Kabeyasawa, Enhancing integrated earthquake simulation with high performance computing, Advances in Engineering Software 42(5) (2011) 286-292.

[12] Wikipedia, Polygonal modeling. http//en.wikipedia.org/wiki/Polygonal_modeling/ 2005.

[13] J. Stoter, S. Zlatanova, 3D GIS, where are we standing, Proceedings ISPRS Workshop on spatial, temporal and multi-dimensional data modelling and analysis, Quebec, Canada 2003.

[14] W. Förstner, 3D-city models automatic and semiautomatic acquisition methods, D. Fritsch, R. Spiller (Eds.), Photogrammetric Week 99, Wichmann Verlag (1999) 291-303.

[15] S. Michihiko, Virtual 3D models in urban design, Virtual Geographic Environment, Hong Kong, China 2008.

[16] M. Batty, D. Chapman, S. Evans, M. Haklay, S. Kueppers, N. Shiode, et al., Visualizing the city communicating urban design to planners and decision-makers, Centre for Advanced Spatial Analysis, University College London, London, UK 2001.

[17] N. Shiode, 3D urban models recent developments in the digital modelling of urban environments in three-dimensions, GeoJournal 52(3) (2000) 263-269.

[18] PLW Modelworks, PLW Modelworks. _http//plwmodelworks.com/ 2014.

[19] CyberCity3D, CyberCity3D. _http//cybercity3d.com/ 2007.

[20] S.R. Hanna, M.J. Brown, F.E. Camelli, S.T. Chan, W.J. Coirier, O.R. Hansen, et al., Detailed simulations of atmospheric flow and dispersion in downtown Manhattan: An application of five computational fluid dynamics models, Bulletin of the American Meteorological Society 87(12) (2006) 1713-1726.

[21] S. You, J.H. Hu, U. Neumann, P. Fox. Urban site modeling from LiDAR, Computational Science and Its Applications¡ªICCSA 2003, Springer Berlin Heidelberg 2003.

[22] Z. Xu, X.Z. Lu, H. Guan, B. Han, A.Z. Ren, Seismic damage simulation in urban areas based on a high-fidelity structural model and a physics engine, Natural Hazards 71(3) (2014) 1679-1693.

[23] Z. Xu, X.Z. Lu, H. Guan, A.Z. Ren, High-speed visualization of time-varying data in large-scale structural dynamic analyses with a GPU, Automation in Construction 42 (2014) 90-99.

[24] Z. Xu, X.Z. Lu, H. Guan, A.Z. Ren, Physics engine-driven visualization of deactivated elements and its application in bridge collapse simulation, Automation in Construction 35 (2013) 471-481.

[25] X.Z. Lu, B. Han, M. Hori, C. Xiong, Z. Xu, A coarse-grained parallel approach for seismic damage simulations of urban areas based on refined models and GPU/CPU cooperative computing, Advances in Engineering Software 70 (2014) 90-103.

[26] Austintexas.gov, GIS/Map Download. ftp://ftp.ci.austin.tx.us/GIS-Data/Regional/coa_gis.html, 2014.

[27] Google, 3D warehouse. https://3dwarehouse.sketchup.com/ 2014.

[28] CyberCity3D, 3D Basic Cities. http://www.cybercity3d.com/newcc3d/index.php/products/item/130-3d-basic-buildings 2014.

[29] M. Barnes, E.L. Finch, Collada-digital asset schema release 1.5.0 specification, Khronos Group, CA, USA 2008.

[30] T. Lee, TinyXML. http//www.grinninglizard.com/tinyxml/ 2007.

[31] A.K. Chopra, Dynamics of structures, Prentice Hall, New Jersey, USA 1995.

[32] L.S. Avila, S. Barre, B. Geveci, A. Henderson, W.A. Hoffman, B. King, et al., The VTK user's guide (VTK 4.2), Kitware Inc., New York, USA 2003.

[33] A.H. Squillacote, The ParaView guide: A parallel visualization application, Kitware Inc., New York, USA 2007.