Experimental Study and Numerical Model Calibration for Earthquake-induced Collapse of RC Frames with Emphasis on Key Columns, Joints and the Overall Structure

Linlin Xie ¹, Xinzheng Lu ^{2, *}, Hong Guan ³, and Xiao Lu ⁴

¹ Department of Civil Engineering, Tsinghua University, Beijing, P.R. China

² Department of Civil Engineering, Tsinghua University, Beijing, P.R. China

³ Griffith School of Engineering, Griffith University Gold Coast Campus, Queensland 4222, Australia

⁴ Department of Civil Engineering, Beijing Jiaotong University, Beijing, P.R. China.

Journal of Earthquake Engineering, 2015, 19:8, 1320-1344. DOI: 10.1080/13632469.2015.1040897.

Download Full Text

Download Test Data Excel Files

Abstract

A thorough investigation of earthquake-induced collapse of reinforced concrete frames is presented. The inherent correlation between the nonlinear behavior of key components and the collapse mechanism of overall frame is examined through concurrent collapse tests of both frame and key components. Important issues in the component models are investigated through calibration against experiments, leading to a comprehensive structural system model. Both test and simulation indicate that the seismic performance are predominately governed by the key columns, whereas the energy dissipation capacity is somewhat affected by the joints. This study offers systematic experimental data and numerical models for future collapse assessments.

Keywords: Structural collapse; RC frame; Experimental calibration; Key components; Joints.

1.       Introduction

Reinforced concrete (RC) frame structures, being one of the most popular structural systems for residential and commercial buildings, often experience severe damage and collapse when subjected to destructive earthquakes (e.g., the Northridge earthquake in 1994, the Kobe earthquake in 1995, the Chi-Chi earthquake in 1999 and the Wenchuan earthquake in 2008) [Swinbanks, 1995; Otani, 1999; Wu et al., 2009; Lu et al., 2012]. In particular, as the most devastating earthquake in China over the past three decades, the Wenchuan earthquake led to the collapse of thousands of RC frames; the event killed 69,195 people and left 18,392 missing and amounted to about 136 billion US dollars losses (http://en.wikipedia.org/wiki/2008_Sichuan_earthquake). Despite being designed following the 2001 version of the Chinese Code for Seismic Design of Buildings (GB 50011-2001) [CMC, 2001] (note that the same design code was revised after the Wenchuan earthquake and subsequently released in 2010 [CMC, 2010a]), the majority of the frames still suffered severe damages. For example, 29.2% of the RC frames in Beichuan City collapsed partially and 33.3% collapsed completely [Civil and Structural Groups of Tsinghua University et al., 2008]. Furthermore, the failure modes observed during the Wenchuan earthquake were inconsistent with those expected. For example, many columns exhibited severe damage, even failure, prior to the beams; and some beam-column joints also experienced different degrees of damage. These phenomena appear to be contradictory to the ¡°strong-column-weak-beam¡± and ¡°strong-joint-weak-member¡± principles expected by the Chinese codes [CMC, 2001, 2010a]. To further investigate the inherent collapse mechanisms of the RC frames damaged during the Wenchuan earthquake, both experiments and numerical simulation are considered necessary to provide a reliable and effective means for damage assessments.

This study thus aims to perform both experimental and numerical investigations on the inherent collapse mechanisms of RC frames and to identify some of the important research challenges and issues. Numerous experimental studies, including static and shaking table tests, have been conducted. These studies can be classified into two categories: at the component level [Beres et al., 1996; Ghannoum and Moehle, 2012a; Elsouri and Harajli, 2013] and at the structural system level [Kabeyasawa et al., 2007; Wu et al., 2009; Moaveni et al., 2010; Panagiotou et al., 2011]. Among these, experimental studies of the overall structures are generally regarded as the most reliable method of investigation. This is because collapse is a global structural behavior featuring a complicated internal force redistribution characteristic during the collapse process. Despite the fact that the entire collapse process can be observed in the structural system level experiments, detailed behavior (e.g., internal forces and dissipated energies) of the individual structural components cannot be readily obtained. Particularly, the correlation between the internal force, deformation, and energy dissipation capacity of the key components and the collapse resistance of the overall structure is difficult to be established. This fact, to some extent, limits (1) in-depth investigations of the inherent collapse mechanisms; (2) identifications of the key components affecting the collapse of the entire structure, (3) further improvements of the key component design, and (4) discussions on the main source of computational errors of a numerical model when its simulation results are inconsistent with the experimental data. Moreover, it has been noted that the damage modes obtained in the experiments are different from the actual ones observed in the Wenchuan earthquake. This is mainly attributed to the differences between the real-world engineering practice and the test frames, including the tie beams, the slabs and other design details. However, such particular design details have rarely been considered concurrently in an investigation.

With regard to the numerical simulation, research to date indicates that it has become increasingly effective to examine the collapse mechanisms of RC frames [Elwood and Moehle, 2008; Haselton, 2008; Haselton et al., 2009; Lynch et al., 2011; Ghannoum and Moehle, 2012b; Kim et al., 2012]. Nevertheless, several critical issues related to the modeling techniques for structural components and the overall system have been identified [Ibarra and Krawinkler, 2005; Ibarra et al. 2005; Lignos and Krawinkler, 2011; Lignos and Krawinkler 2012]. Deierlein and his colleagues [Haselton, 2008; Haselton et al., 2009] indicated that when simulating an earthquake-induced structural collapse, nonlinear behavior of all the structural components must be comprehensively considered. Two critical challenges must also be addressed for a rational and accurate simulation: (1) Advanced component models for RC beams, columns and joints are necessary to capture the characteristic behavior of an RC frame, from elastic to yield, and finally to collapse. (2) The key parameters of these models must be calibrated based on the data from carefully designed experiments. To address these challenges, a number of beam-column models [Spacone et al., 1996; Ibarra et al., 2005] and joint models [Alath and Kunnath, 1995; Altoontash, 2004; Mitra and Lowes, 2007; Park and Mosalam, 2013] have been proposed in recent decades. However, due to the complicated nature of RC frames, without accurate calibrations using detailed experimental data, it is rather difficult to identify the most appropriate component model capable of simulating the collapse behavior accurately. Similarly, it is also hard to evaluate the critical parameters in the models without a set of benchmarking experimental data. In consequence, in the absence of the rational component models, the reliability of the prediction results at the structural system level is also doubtful. Therefore, to evaluate the rationality of the component models and the corresponding structural model, as well as the accuracy of the prediction results and the reliability of the conclusions drawn from the analysis, further experimental studies and comprehensive model calibration based on available database [Panagiotakos and Fardis, 2001; Lignos and Krawinkler, 2012; Perus et al. 2014] are considered necessary and critical.

As described above, a carefully designed experimental program covering both the overall frame and the key components is valuable for understanding the collapse mechanisms and calibrating the numerical models of RC frames. Due to limited work on such experiments and model calibration, the focus of this study is thus to perform a series of pseudo-static collapse experiments and numerical model calibrations concurrently for both the key components and the overall frame. Damage mechanisms of the RC frames exhibited in the Wenchuan earthquake will also be thoroughly investigated. Specifically, four innovations of the proposed experimental research are highlighted herein: (1) concurrent experiments on the key components and the overall frame are performed to investigate the correlation between the nonlinear behavior of the key components and the collapse mechanism of the structure; (2) the loading condition and the detailed design parameters of the key components are assumed to be identical to the corresponding components in the overall frame; (3) to better replicate the real-world engineering practice, a tie beam is designed at the bottom of the column to examine its constraint effect to the columns; (4) the frame beam is designed as a T-shaped section to account for the contribution of slabs, and the flange width is set to be 6 times of the slab thickness in accordance with the Chinese Concrete Design Code [CMC, 2002]. In the proposed numerical simulation, the accuracy, stability and robustness of different numerical component models and the associated material models are evaluated based on the detailed experimental data. Consequently, the appropriate component models can then be recommended. Based on these component models, a structural system model, considering all the possible nonlinear factors associated with the collapse of RC frames, is successfully proposed to simulate the entire collapse process. The research outcome of this study will provide an in-depth understanding of the inherent collapse mechanisms of similar RC frames during strong earthquakes, and will also offer systematic experimental data and reference numerical models for future collapse assessments of such structures.

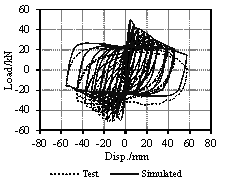
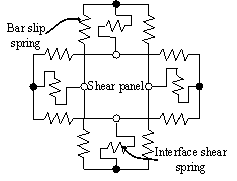
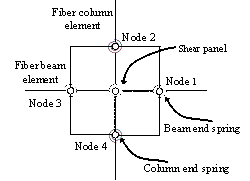
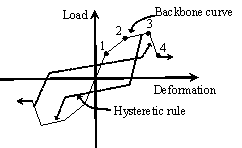
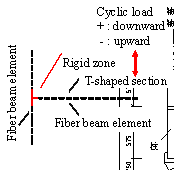
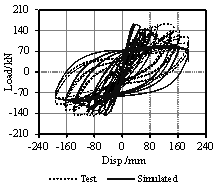
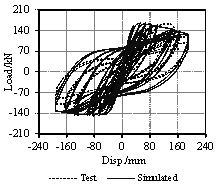
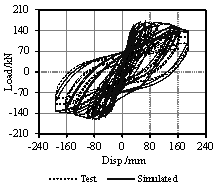
2.       Pseudo-Static Collapse Experiments

2.1.  Design of Half-Scale Prototype

This research focused on the investigation of the collapse mechanisms of RC frames damaged during the Wenchuan earthquake. The frames concerned were constructed in accordance with the 2001 version of the Chinese Seismic Design Code [CMC, 2001]. A prototype model, i.e. a 3-span 6-story RC frame, is herein designed following the Chinese codes [CMC, 2001, 2002]. The prototype frame is located on a site with a seismic design intensity of seven (the peak ground acceleration (PGA) is 200 cm/s² for 10% probability of exceedance in 50 years) and a site classification of II (i.e., an equivalent shear-wave velocity of 360 m/s for 30 m soil (V_S30)). The dimensions and design strengths of the prototype frame are summarized in Table 1. The dead and live loads are 4.6 kN/m² and 2.0 kN/m², respectively. According to the Chinese Code for Seismic Design of Buildings (GB50011-2001) [CMC, 2001], the design axial load ratio calculated using Eq. (1) is found to be approximately 0.8 for the middle column on the first story.

                                                           (1)

in which n is the design axial load ratio; DL and LL are respectively the dead load and live load of the building for seismic design; g_DL (= 1.2) and g_DL (= 1.4) are the partial factors for dead load and live load, respectively; f_c is the concrete compressive strength; g_c (= 1.4) is the partial factor of concrete strength. Note that the actual axial load ratio without considering the partial factors is approximately 0.395. The corresponding axial forces are approximately 1304 kN in the prototype and 326kN in the test frame, respectively. The PKPM [CABR, 2010] software is employed to perform reinforcement design.

TABLE 1: Dimensions and design strengths of the prototype frame

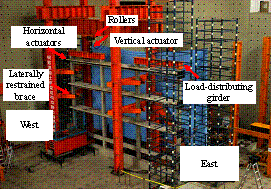
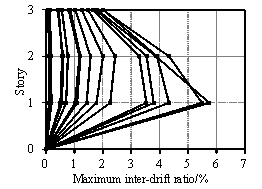
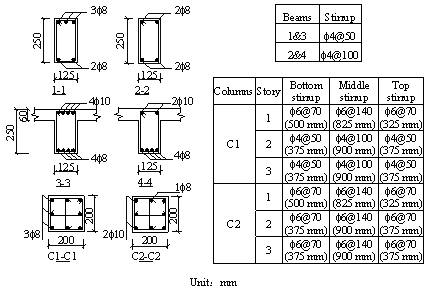
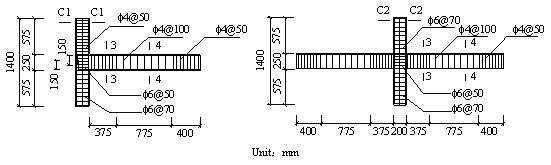
To better represent the behavior of the real structure, the size of the model is designed as large as possible to make full use of the loading capacity of the testing equipment. Considering the height limitation of the strong reaction wall in the laboratory, a half-scaled model is adopted. Such scale is also used by other researchers [Elwood and Moehle, 2008]. The dimensions and reinforcement details of the scaled model are presented in Figure 1. The load pattern of the experiment is illustrated in Figure 2(a), where the upper three stories are simplified into four concentrated loads applied downward by two vertical actuators and two load-distributing girders. Each actuator provides a 489 kN vertical load at the one-third point of the corresponding load-distributing girder, which makes a 2:1 proportion of the axial forces in the middle-columns (Columns 2 and 3) and those in the side-columns (Columns 1 and 4). Rollers, as shown in Figure 2, are installed to ensure that the vertical actuators could translate horizontally together with the roof. The vertical loads provided by the actuators are measured throughout the test. The maximum variation of the axial loads during the test is less than 2% of the expected axial load, suggesting that the actuators are able to stably provide constant vertical loads. The proportion of the designed seismic forces from the sixth to the first story of the prototype is 6:5:4:3:2:1. Note that only the bottom three stories are tested, therefore all of the seismic forces sustained by the upper three stories are applied to the top of the third story. Hence, three cyclic lateral loads with a proportion of 18:2:1 are applied by the three horizontal actuators at the third, second and first story to conduct a cyclic static experiment, as illustrated in Figure 2(a). Figure 2(b) shows the experimental setup of the scaled frame. Four laterally restrained braces are used to limit the out-of-plane displacement of the frame. The entire loading process is controlled by the displacement of the top floor, and a mixed control test program is adopted to ensure the proportionality of three horizontal loads. The lateral loading are selected in accordance with the protocols specified in the Specification of Testing Methods for Earthquake Resistant Building (JGJ 101-96) [CMC, 1997], as shown in Figure 2(c).

Prior to the experiment, concrete cubes of 150 ¡Á 150 ¡Á 150 mm were casted and tested in accordance with the provisions of the Standard for Test Method of Concrete Structures (GB50152-2012) [CMC, 2012]. The measured compressive strengths are given in Table 2. The characteristic properties of the reinforcing steel with a gauge length of 350 mm following the Chinese Code (GB 228.1-2010) [CMC, 2010b] were experimentally measured and summarized in Table 3.

TABLE 2: Compressive strength of concrete

*f_{cu, 150mm} is the compressive strength of concrete cubes with a size of 150 mm.

TABLE 3: Properties of reinforcing steel

*f_y and f_u are the yield and ultimate strengths of the reinforcing bars, respectively.

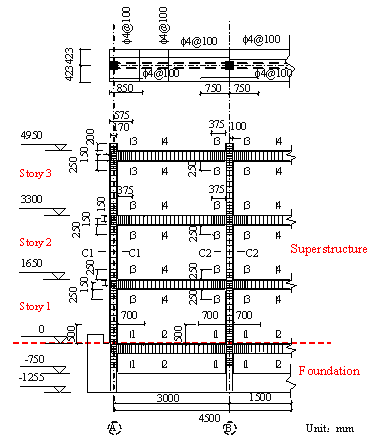
(a)     

(b)    

(c)     

FIGURE 1: Dimensions and reinforcement details of the scaled frame: (a) frame, (b) beams/columns and (c) joints.

FIGURE 2: Test setup of the overall frame: (a) load pattern of the experiment, (b) experimental setup of the overall frame and (c) lateral loading protocol

2.2.  Design of Half-Scale Key Components

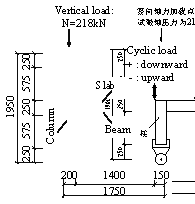
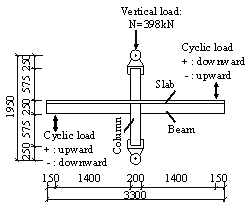
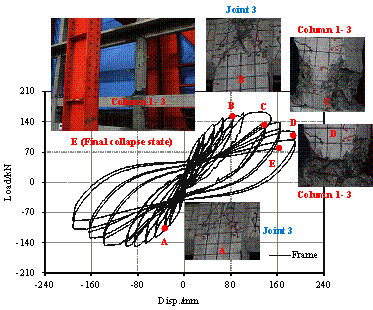
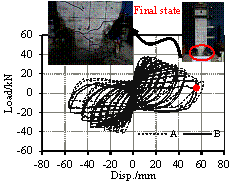
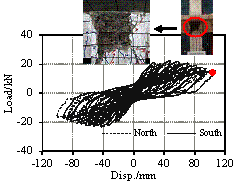
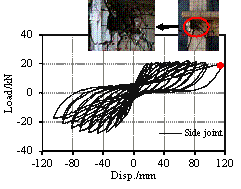
Damage modes observed in the Wenchuan earthquake and the preliminary numerical analysis [Tang, 2011] prior to the proposed tests have both revealed two notable characteristics: (1) the bottom of the columns on the first story exhibited severe damage, which may trigger the collapse of the overall structure; (2) the beam-column joints on the first story also experienced severe damage, which may affect the seismic performance of the overall structure. In consequence, to investigate the inherent correlation between the nonlinear behavior of these key structural components and the collapse mechanism of the overall structure, four frame columns and two beam-column joints on the first story are selected for the key component tests. These six specimens include two identical side columns, two identical middle columns, one side joint and one middle joint, as indicated in Figure 3. Note that the detailed design information of these components is identical to the corresponding components in the overall frame. Furthermore, based on the actual compressive strengths, the vertical loads applied to the key components are adjusted to ensure that the axial load ratios are consistent with those of the corresponding components in the overall structural test (see Table 4).

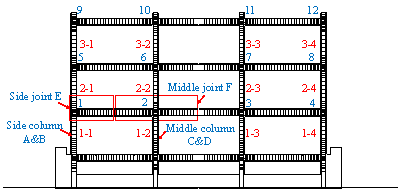
FIGURE 3: Locations of the selected key components

TABLE 4: Compressive strengths of concrete and axial forces for each specimen

With regard to the collapse performance assessment for RC frames, Haselton et al. [2009] recommended that the components should be tested until the large deformation stage so that their near-collapse responses can be clearly observed. In view of this, the proposed test should be beneficial for (1) further understanding of the inherent collapse mechanisms of RC frames, and (2) more accurate calibrations of the numerical component models. As such, in this work, the columns are designed to be continuously loaded when the bearing capacity drops to 85% of the peak force, and the tests are not terminated until the columns completely lose their vertical load carrying capacity (i.e., the near-collapse state).

Note that the assumption of the constant vertical load may simplify the loading condition, although it may not fully represent the columns in the actual frame. Given that the constant loading condition has been proven to be capable of representing the characteristic behavior of RC components [Maruyama et al., 1984; Bousias et al., 1995; Qiu et al., 2002; Elsouri and Harajli, 2013], such a loading condition is therefore adopted to conduct the proposed tests of key components, and the constant load as given in Table 4 is applied at the top of the columns by an axial hydraulic actuator.

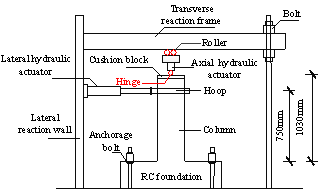
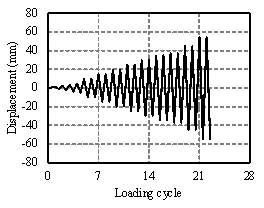
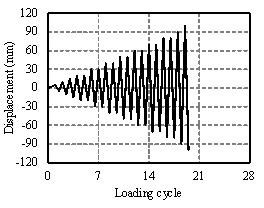
The test setup and the lateral loading protocols of the columns and joints are presented in Figure 4 and Figure 5, respectively. The constant vertical loads applied to the side joint and middle joint are 218 kN and 398 kN, respectively (Table 4). The seismic forces are simulated by gradually incremental loads or displacements at the beam ends. In this work, a slow loading velocity with a maximum value of 0.2 mm/s (i.e., nearly 15 minutes per cycle) is adopted to conduct the quasi-static tests. For such a slow loading velocity, the loading-rate effect can be negligible [Ghannoum et al. 2012].

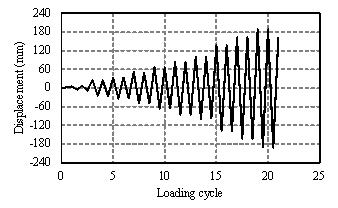
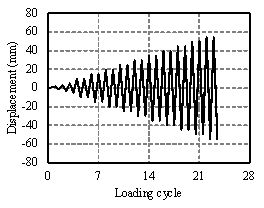
FIGURE 4: Test setup of the columns: (a) diagram of the experimental device, (b) photograph of the experimental device, (c) lateral loading protocol of side columns and (d) lateral loading protocol of middle columns

FIGURE 5: Test setup of the joints (mm): (a) diagram of the experimental device of Side joint E, (b) diagram of the experimental device of Middle joint F, (c) photograph of the experimental device of Side joint E, (d) photograph of the experimental device of Middle joint F, (e) vertical loading protocol of Side joint E and (f) vertical loading protocol of Middle joint F

3.       Test Observations and Analysis of the Experimental Data

For the overall frame test, diagonal cracks (point A in Figure 6) appeared at the middle joints of the first story when the displacement of the top floor reached 33 mm. When the frame experienced a drift ratio of 2% (i.e., when the peak displacement of the top floor reached 84 mm), which is the maximum allowable drift ratio specified in the Chinese seismic design code [CMC, 2001] for RC frames, concrete crushing was obvious at the bottom of the side and middle columns, and concrete peeling took place at the joints (point B in Figure 6). When the frame experienced a peak drift ratio of 3.85% (i.e., when the peak displacement of the top floor reached 139 mm), severe concrete spalling was noticed on the cover layer at the bottom of Column 1-3 (point C in Figure 6). Finally, when the peak displacement of the top floor reached 190 mm, the bottom of Column 1-3 experienced a large vertical deformation (point D in Figure 6) and concrete at the bottom of the column completely crushed. At this stage, the vertical loads applied to the top floor could no longer be maintained. Consequently, the overall structure reached the collapse state. The base shear force-top displacement hysteretic curve and the photos of each key state (points A, B, C and D) are presented in Figure 6.

FIGURE 6: Base shear force-top displacement hysteretic curve and damage states of the overall frame

Based on the above-mentioned experimental observations, the following conclusions can be drawn:

1.      The bottom of the columns on the first story experienced the most severe damage.

2.      The joints on the first story exhibited severe damage, while those on the second story experienced different degrees of damage.

3.      The response of the overall structure exhibited a significant shear deformation mode, which could be observed from Figure 7. Such a deformation was dominated by the inter-story drift ratio of the first story, and this phenomenon became more obvious with increased peak displacement.

FIGURE 7: Maximum inter-story drift ratio of each loading cycle

Ultimately, the loss of vertical load carrying capacity of Column 1-3, which was triggered by the complete crushing of the column bottom, initiated the collapse of the overall frame.

Specifically for the key columns, when the side and middle columns experienced drift ratios of 5.7% and 5.56%, respectively (i.e., when the top displacement of the columns reached 60 mm and 57 mm), their lateral load carrying capacity were completely lost. In addition, these columns were no longer capable of maintaining the vertical load due to the P-D effect, thus leading to the collapse of these columns. The failure modes of the key columns are consistent with those observed in the overall frame test. The lateral load-displacement relation curves of the two side columns (A and B) and the two middle columns (C and D) are presented together in Figures 8(a) and (b), respectively. Due to the similarity of the failure phenomena of the two side (middle) columns, only two photos are presented in Figure 8 for Side column B and Middle column D. It can be found from the figure that the middle columns reach a slightly higher peak load but a lower ductility in comparison with the side columns. This is because the middle columns are designed with a higher reinforcement ratio and a larger axial compression ratio.

FIGURE 8: Lateral load-displacement relation and failure phenomena of (a) side columns and (b) middle columns

With regard to the key joints, both the side and middle joints experienced severe damage. The joint cores exhibited numerous intersecting cracks, and complete concrete cover spalling together with stirrup exposure. When the actuators reached their maximum capacities, the experiment was terminated. The vertical load-displacement curves and the typical failure phenomena are plotted in Figure 9. Note that the Middle joint F has two beam ends (i.e., the north and south ends as shown in Figure 5(d)), and their vertical load-displacement curves are presented in Figure 9(a). Figure 9(b) plots the same for the Side joint E. The key joint tests indicate that the damage of the joints is much severer than that of the adjacent beams and columns. This phenomenon is consistent with the damage mode observed in the overall frame test, further validating that the expected ¡°strong-joint-weak-member¡± failure mode cannot be attained.

FIGURE 9: Vertical load-displacement curves of the beam ends and typical failure phenomena of (a) Middle joint F and (b) Side joint E

4.       Numerical Analysis of the Pseudo-Static Collapse Tests

Accurate and efficient nonlinear structural component models and the associated material models are critical issues to be considered in simulating earthquake-induced collapses of RC frames. To examine the accuracy, stability and reliability of different component models (e.g., the BeamColumnJoint or Joint2D model that will be discussed later) and the corresponding methods for evaluating the key parameters of the material models (e.g., the ductility of confined concrete of column), comparisons with the experimental data of the key component tests are conducted. Appropriate component models for the collapse simulation of RC frames are subsequently summarized. Further, a comprehensive structural system model, integrating these component models, are proposed and validated through comparison with the experimental data of the overall frame. The correlation between the failure modes of the key components and the collapse mechanism of the structure is further identified through these numerical analyses.

As an object-oriented open source FE software program, the Open System for Earthquake Engineering Simulation (OpenSees) (http://opensees.berkeley.edu) is a versatile tool for numerical simulation. It incorporates various types of materials, elements, and powerful algorithms, thus allowing flexible definition of the numerical models satisfying specific requirements of different research projects. OpenSees has also become increasingly popular, being as one of the most influential platforms for nonlinear seismic analyses of various types of structures [Elwood and Moehle, 2008; Haselton, 2008; Haselton et al., 2009; Lignos et al., 2011a]. Because of these advantages, OpenSees is adopted in this study to conduct the collapse assessment of RC frames.

4.1.  Model Calibration for RC Columns

The Wenchuan earthquake and the overall frame test both indicate that the columns in RC frames mostly exhibit a flexural-dominated failure mode. To simulate such a failure mode, various finite element models have been proposed. These include the fiber beam model [Spacone et al., 1996; Tram and Kasai, 2011] and the lumped plasticity model [Ibarra et al., 2005; Lignos et al., 2011b; Lignos et al., 2013]. Through a regression analysis of 255 RC column elements with different design and detailing characteristics, a strategy for selecting the key parameters for a typical lumped plasticity model (i.e. the modified Ibarra-Medina-Krawinkler deterioration model) [Ibarra et al., 2005] was proposed by Deierlein and his colleagues [Haselton, 2008; Haselton et al., 2009]. This lumped plasticity model was then used for the collapse simulation and assessment of a 3-span 4-story plane RC frame [Haselton, 2008; Haselton et al., 2009]. Nevertheless, this model is incapable of taking into account biaxial bending and the variation of axial forces. As an alternative, the fiber beam model can capture the coupled biaxial bending/axial force behavior [Spacone et al., 1996]. As such, the fiber beam model is adopted herein to simulate the key columns. It should be noted that further validation is required to confirm the capacity of the fiber beam model in simulating the collapse behavior of RC frames, as suggested by Haselton et al. [2009]. Specifically, it is well acknowledged that the plastic deformation capacity of RC columns can be effectively improved by considering the confinement effect of the stirrups [Mander et al., 1988; L¨¦geron et al., 2005; Lu et al., 2013]. Despite numerous stirrup-confined concrete models are available, further validation against the experimental data is required to determine the most appropriate model for simulating RC columns and frames at the near-collapse state [Haselton et al., 2009]. Moreover, the capacity of the existing large deformation algorithms must also be further validated at the near-collapse state.

Given the abovementioned requirements, the unconfined and various confined concrete models (including the Legeron [Legeron et al., 2005] and the Mander confined concrete models [Mander et al., 1988]) are compared using Middle column C as an example. Concrete and reinforcing steels are respectively simulated with Concrete01 and Steel02 in OpenSees. Relevant material parameters of concrete are presented in Table 5. The modeling strategy proposed by Scott and Hamutçuoğlu [2008] is adopted to simulate this column. Specifically, the column is modeled with five displacement-based beam-column elements (i.e. DispBeamColumn element in OpenSees), each of which has five integration points [Scott and Hamutçuoğlu, 2008]. Additionally, the ¡°PDelta¡± algorithm of OpenSees is used to consider the effect of large deformations. A comparison between the experimental data and the simulation results using different concrete models is presented in Figure 10 (a-c). Figure 10(a) indicates that the strength deterioration is overestimated without the consideration of the confinement effect, leading to underestimation of the column resistance. Figure 10(b) demonstrates that the Legeron confined concrete model underestimates the softening speed and overestimates the ductility. In contrast, the predicted backbone curve and hysteresis loops using the Mander confined concrete model are compared to the test data in Figure 10(c) with close agreement. The predicted results exhibit a higher stiffness compared to that of the experimental data, a finding similar to those obtained by other researchers [Yavari et al., 2009; Calabrese et al., 2010]. The discrepancy in stiffness produced in this work is not larger than those found in the existing literature and is therefore considered acceptable. Given that the bar-slip effect at the footing interface could to some extent affect the structural stiffness, a simulation accounting for the bar-slip effect could lead to a better agreement with the experiments [Saatcioglu et al., 1992]. The finite element discretization for the fiber element, including the numbers of segments and fibers, does have a direct impact on the accuracy of the simulation. Hence, an in-depth investigation of the finite element discretization is conducted. A benchmark model meshed with 5 elements is established which is also associated with the Mander confined concrete model [Mander et al., 1988]. To discuss the influence of the number of segments, three discretization schemes (i.e. 3, 5 and 10 elements) are considered. A comparison of the simulation results, presented in Figure 10(d), indicates that the number of segments somewhat affect the slope of the softening branch. Nonetheless, all of the three schemes are capable of capturing the characteristic behavior of the near-collapse RC columns. To examine the influence of the number of fibers, three discretization schemes (i.e. 45, 140 and 560 fibers) are also considered. The simulation results are compared in Figure 10(e) showing a close agreement. This implies that the number of fibers has negligible influence on the predicted hysteretic behavior of the columns. Based on the above simulation of Middle column C, it can be concluded that the accuracy of the simulation results relies largely on the confined concrete model adopted for the concrete fibers, and to some extent is affected by the number of segments. The number of fibers, on the other hand, has negligible influence on the accuracy of the predicted results.

TABLE 5: Parameters of the backbone curves of the confined concrete models

FIGURE 10: Comparison of the hysteretic curves of Middle column C using (a) unconfined concrete model, (b) Legeron model, (c) Mander model, (d) Mander model with different number of segments and (e) Mander model with different number of fibers

Based on this validation, the Mander confined concrete model is adopted to simulate all of the key columns. The comparisons between the experimental data and simulation results are presented in Figure 11. Good agreements are also achieved for all these columns. This outcome confirms that the strength deterioration observed in the tests can be well captured using the fiber beam model. The backbone curve and the hysteretic behavior are also proven to agree well with the experimental data, thus conclusively validating the reliability of the fiber beam model in simulating the near-collapse RC columns dominated by the flexural behavior.

FIGURE 11: Comparison of the hysteretic curves of (a) Side column A, (b) Side column B and (c) Middle column D using Mander confined concrete model

4.2.  Model Calibration for Beam-Column Joints

Despite being designed following the principle of ¡°strong-joint-weak-member¡± according to the Chinese seismic design code [CMC 2001], the Wenchuan earthquake destruction and laboratory tests both indicate that the joints exhibited severe damage. In consequence, the nonlinear behaviors of the joints are required to be considered in the collapse simulation and assessment of RC frames. Although various joint models have been proposed to date [Alath and Kunnath, 1995; Altoontash, 2004; Mitra and Lowes, 2007], validation against the experimental data is desirable to determine the most appropriate model for the simulation of RC joints, in terms of the accuracy, stability and reliability. Furthermore, an appropriate joint model should be capable of simulating three possible failure modes in numerical analyses [Altoontash, 2004; Mitra and Lowes, 2007]. These failure modes are (1) shear failure of the joint core, (2) anchorage failure of the frame-member longitudinal reinforcement embedded in the joint, and (3) shear-transfer failure at the joint-beam and joint-column interfaces. Subsequently, different joint models and the associated material models are calibrated based on the experimental data of the key joints obtained earlier in this study. In addition to evaluating an appropriate joint model, this study also lays a foundation for further investigations of the influence of joint damage on the global deformation and the collapse resistance of the overall frame.

4.2.1.          Numerical models for RC joints

The joint models proposed over the last four decades can be divided into two categories. The first category of the model uses a single nonlinear spring to represent all the potential failure modes of the joints [Alath and Kunnath, 1995; Park and Mosalam, 2013]. An obvious drawback of this model is that calibration of the parameters of the nonlinear spring is rather difficult, considering the various failure modes of different joints. The second category comprises a set of springs that respectively represent the abovementioned three types of failure modes, viz. (1) the shear-panel springs to simulate the shear failure of the joint core, (2) the bar-slip springs to simulate the anchorage failure of frame-member longitudinal reinforcement, and (3) the interface-shear springs to simulate the shear-transfer failure at the joint-beam and joint-column interfaces [Altoontash, 2004; Mitra and Lowes, 2007]. Having different types of springs for different failure modes instead of a single spring for all the failure modes makes the parameter calibration much easier. Two typical joint models in the second category have been proposed and are available in OpenSees: the BeamColumnJoint element [Mitra and Lowes, 2007] and the Joint2D element [Altoontash, 2004]. The BeamColumnJoint element includes one shear-panel spring, four pairs of bar-slip springs and four interface-shear springs, as shown in Figure 12(a). Based on the BeamColumnJoint element, the Joint2D element, a simplified model with five springs, was proposed by Altoontash [2004]. This is presented in Figure 12(b). In comparison with the BeamColumnJoint element, four simplified springs are introduced in the Joint2D element to replace the four pairs of bar-slip springs to account for the anchorage failure. Note that the Joint2D element is capable of simulating the influence of large deformations on the behavior of the joints.

FIGURE 12: Components of (a) the BeamColumnJoint element and (b) the Joint2D element

To simulate the strength and stiffness deterioration due to the shear failure of the joint core, the Pinching4 material in OpenSees (Figure 13) with a softening branch is adopted to model the shear-panel spring of both BeamColumnJoint and Joint2D elements. A critical issue for the Pinching4 material is how to determine its backbone curve. The modified compression field theory (MCFT) model [Vecchio and Collins, 1986] and the fixed-angle soften truss model (FA-STM) [Hsu, 1997] are usually recommended to calculate the key parameters of this curve, and the hysteretic rules associated with the strength and stiffness deterioration proposed by Stevens et al. [1991] are adopted to represent the response under cyclic loading. The other types of springs in the BeamColumnJoint and Joint2D elements are simulated using the modeling approaches proposed by Mitra and Lowes [2007] and Altoontash [2004], respectively.

FIGURE 13: Hysteretic model for the Pinching4 material

4.2.2.          Model evaluation and verification

To investigate the influence of the nonlinear response of the joint, only the fiber beam model is adopted herein to simulate Side joint E, as shown in Figure 14(a). This implies that the joint zone is rigid and its nonlinear behavior is neglected. The simulation results are compared in Figure 14(b) with the experimental data, where a significant discrepancy is observed. This is because without consideration of the nonlinear behavior of the joint, the predicted failure mode is a flexural failure at the ends of the beams and columns. This is unlike the shear failure mode within the joint core as observed during the test. As such, the nonlinear behavior of the joint must not be neglected in seismic performance assessments of such a specimen.

FIGURE 14: Simulation of Side joint E without considering nonlinear effect of the joint: (a) FE model system and (b) comparison between the experimental data and simulation results

An integrated model encompassing the fiber beam model and the joint model, respectively for the beams/columns and the joints, is proposed to simulate the key joints. The abovementioned two elements (i.e., the BeamColumnJoint and Joint2D elements are adopted for each joint model, and two material models (i.e., the MCFT model and FA-STM) are used to evaluate the envelopes of the shear stress-strain of the shear-panel spring. Of the four combinations of the two elements and two material models, the most suitable combination for simulating the behavior of the joints and the overall RC frame needs to be identified. This is achieved by calculating the stress and strain at four key points on the shear stress-strain curve of the shear-panel spring, as indicated in Figure 13. The calculated values using the MCFT model and FA-STM are presented in Table 6. To compare the accuracy, reliability and robustness of different models, identical numerical solution parameters, including the maximum iterative steps and the tolerance of errors are adopted for all of the numerical simulations.

TABLE 6: Parameters of the backbone curves of the shear panel spring

Taking the Middle joint F as an example, comparisons between the experimental data and the simulation results using the BeamColumnJoint element associated with the MCFT model and FA-STM are presented respectively in Figure 15 and Figure 16. The following conclusions can be drawn:

1.      The significant pinching phenomena caused by the shear failure of the joint core can be well represented by the combinations of the BeamColumnJoint element and the MCFT model or FA-STM. A high computational stability and robustness can also be achieved.

2.      When the Middle joint F approaches the negative displacement of 54 mm, the shear deformation of the joint core reaches its ultimate value when FA-STM is used. The analysis is subsequently terminated, leading to an underestimation of the deformation capability of the joint. In contrast, the predictions using the MCFT model agree relatively well with the test data.

FIGURE 15: BeamColumnJoint element using the MCFT model: (a) north side of Middle joint F and (b) south side of Middle joint F

FIGURE 16: BeamColumnJoint element using the FA-STM model: (a) north side of Middle joint F and (b) south side of Middle joint F

Given that the MCFT model performs better than FA-STM, a comparison between the experimental data and the simulation results using the Joint2D element associated with the MCFT model only is presented in Figure 17. Due to the fact that the large deformation algorithm is implemented in the Joint2D element, the strength deterioration experienced in the test can be well simulated when the negative displacement is larger than 60 mm. Nevertheless, the hysteretic behaviors predicted by the Joint2D element differ a lot from the test. Furthermore, the Joint2D element is proven to be relatively unstable, and a numerical convergence is difficult to be achieved for this middle joint specimen.

FIGURE 17: Joint2D element using the MCFT model: (a) north side of Middle joint F and (b) south side of Middle joint F

Using the BeamColumnJoint element in conjunction with the MCFT model, the simulation of Side joint E is also conducted. The experimental data and simulation results are compared in Figure 18 with close agreement, thus further validating the reliability and stability of the adopted models in simulating the seismic behaviors of RC joints.

FIGURE 18: Side joint E with the BeamColumnJoint element

The above calibrations, in terms of the accuracy, stability and robustness, confirm that the BeamColumnJoint element associated with the MCFT model performs the best among all the model combinations. Particularly, with regard to the numerical stability which is a critical issue for simulating the nonlinear behavior of joints and overall structure, the BeamColumnJoint element in conjunction with the MCFT model is able to reach a converged solution. Hence, it is recommended to be used for the collapse simulation of the overall RC frame.

4.3.  Model Calibration for the Simulation of the RC Frame

The component models validated above are thus used to simulate the overall RC frame. Note that the loading scheme of the simulation is identical to that of the test. To account for the influence of the slabs, the beams are simulated using the fiber beam model with a T-shaped section. Three models (A, B and C) are established to investigate the influence of different modeling strategies, as summarized in Table 7. Model A does not taken into account the confinement effect of concrete and the nonlinear behavior of joints. Model B considers the confinement effect only using the Mander confined concrete model. Model C is a comprehensive structural system model, integrating the fiber beam elements with the Mander confined concrete model and the BeamColumnJoint elements associated with the MCFT model.

TABLE 7: Case study

Comparisons between the hysteretic base shear force-roof displacement relation curves obtained from the experiment and predicted by the three models are presented in Figure 19. Figure 19(a) indicates that the strength deterioration is overestimated by Model A without the consideration of the confinement effect, leading to an underestimation of the seismic resistance of the overall frame. On the other hand, the backbone curve predicted by Model B is in a close agreement with the experimental results (Figure 19(b)), even though the nonlinear behavior of the joints is not considered in this model. This outcome suggests that the resistance and the deformation capacity of the frame are predominately governed by the nonlinear behavior of the key columns and are mostly affected by the confined concrete model adopted.

FIGURE 19: Comparison between the experimental data and the predicted results: (a) Model A, (b) Model B and (c) Model C

Notwithstanding the above, there are still some discrepancies between the experimental and the simulated hysteretic behaviors of Model B. In particular, Model B is incapable of capturing the pinching phenomenon observed in the test. The most satisfactory model to simulate the experimental hysteretic behavior is Model C which employs the joint elements. Figure 19(c) indicates that the energy dissipation capacity of the frame is indeed to a certain extent affected by the damage of the joints. It is worth mentioning that the backbone curves of Model C and Model B are almost identical and the beams strengthened by the slabs do not sustain degradation. This further validates that the resistance and the deformation capacity of the frame are predominately governed by the nonlinear behavior of the key columns.

5.       Conclusions

The overall frame test indicates that severe damages mainly occur at the column ends and the joint cores. This further confirms that the expected ¡°strong-column-weak-beam¡± and ¡°strong-joint-weak-member¡± failure modes according to the Chinese codes [CMC 2001, 2002] cannot be achieved. To further investigate the influence of the nonlinear behavior of the columns and the joints on the structural collapse mechanisms, experiments of the key components are also conducted, and their failure modes are proven to be consistent with those observed in the overall frame test. Conducting these experiments concurrently provides systematic experimental data which are valuable for the development and validation of the numerical models at both the component and structural system levels.

The critical issues associated with the numerical modeling strategies for the components and the structural system are discussed in-depth using the systematic experimental data obtained. At the component level, (1) the fiber beam element using the Mander confined concrete model is recommended to simulate flexural-dominated columns; (2) the nonlinear behavior of the joints must be considered; (3) the BeamColumnJoint element associated with the MCFT model is recommended for the joints. Using these validated component models, a comprehensive structural system model, integrating the fiber beam model for the columns/beams and the BeamColumnJoint element for joints is proposed to simulate the collapse of RC frames. Good agreement is achieved between the experimental data and the simulation results. In addition to providing further understanding of the collapse mechanisms of RC frames, this study also offers systematic experimental data and reference numerical models for future collapse assessments of similar RC frames.

Acknowledgement

The authors are grateful for the financial support received from the Beijing Natural Science Foundation (No. 8142024), the National Key Technology R&D Program (No. 2013BAJ08B02) and the National Natural Science Foundation of China (No. 51222804, 51378299).

References

Alath, S. and Kunnath, S. K. [1995] ¡°Modeling inelastic shear deformation in RC beam-column joints engineering mechanics,¡± Proceedings of 10th Conference: University of Colorado at Boulder, Boulder, Colorado 2, 822-825.

Altoontash, A. [2004] ¡°Simulation and damage models for performance assessment of reinforced concrete beam-column joints,¡± Ph.D. Dissertation, Stanford University, California, USA.

Beres, A., Pessiki, S. P., White, R. N. and Gergely P. [1996] ¡°Implications of experiments on the seismic behavior of gravity load designed RC beam-to-column connections,¡± Earthquake Spectra 12(2), 185-198.

Bousias, S. N., Verzeletti, G., Fardis, M. N. and Gutierrez, E. [1995] ¡°Load-path effects in column biaxial bending with axial force,¡± Journal of Engineering Mechanics 121(5), 596-605.

CABR [2010] ¡°User guide documentation of PKPM Software,¡± China Academy of Building Research, Beijing, China.

Calabrese, A., Almeida, J. P. and Pinho, R. [2010] ¡°Numerical issues in distributed inelastic modeling of RC frame elements for seismic analysis,¡± Journal of Earthquake Engineering 14(S1), 38-68.

Civil and Structural Groups of Tsinghua University, Xinan Jiaotong University and Beijing Jiaotong University [2008] ¡°Analysis on seismic damage of buildings in the Wenchuan Earthquake,¡± Journal of Building Structures 29(4), 1-9. (in Chinese)

CMC [1997] ¡°Specification of testing methods for earthquake resistant building (JGJ 101-96,¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China (In Chinese).

CMC [2001] ¡°Code for Seismic Design of Buildings (GB50011-2001),¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China.

CMC [2002] ¡°Code for Design of Concrete Structures (GB50010-2002),¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China.

CMC [2010a] ¡°Code for Seismic Design of Buildings (GB50011-2010),¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China.

CMC [2010b] ¡°Code for Metallic Materials Tensile Testing: Part I: Method of Test at Room Temperature (GB228.1-2010),¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China (in Chinese).

CMC [2012] ¡°Standard for Test Method of Concrete Structures (GB50152-2012),¡± China Ministry of Construction, China Architecture and Building Press: Beijing, China.

Elsouri, A. M. and Harajli, M. H. [2013] ¡°Seismic response of exterior RC wide beam-narrow column joints: earthquake-resistant versus as-built joints,¡± Engineering Structures 53, 394-406.

Elwood, K. J. and Moehle, J. P. [2008] ¡°Dynamic collapse analysis for a reinforced concrete frame sustaining shear and axial failures,¡± Earthquake Engineering & Structural Dynamics 37(7), 991-1012.

Ghannoum, W. M., Moehle, J. P. and Bozorgnia, Y. [2008] ¡°Analytical collapse study of lightly confined reinforced concrete frames subjected to Northridge earthquake ground motions,¡± Journal of Earthquake Engineering 12(7), 1105-1119.

Ghannoum, W., Saouma, V., Haussmann, G., Polkinghorne, K. and Kang, D. H. [2012] ¡°Experimental investigations of loading rate effects in reinforced concrete columns,¡± Journal of Structural Engineering 138(8), 1032-1041.

Ghannoum, W. M. and Moehle, J. P. [2012a] ¡°Shake-table tests of a concrete frame sustaining column axial failures,¡± ACI Structural Journal 109(3), 393-402.

Ghannoum, W. M. and Moehle, J. P. [2012b] ¡°Dynamic collapse analysis of a concrete frame sustaining column axial failures,¡± ACI Structural Journal 109(3), 403-412.

Haselton, C. B. [2008] ¡°Beam-column element model calibrated for predicting flexural response leading to global collapse of RC frame buildings,¡± Pacific Earthquake Engineering Research Center, Berkeley, CA.

Haselton, C. B., Liel, A. B. and Deierlein, G. G. [2009] ¡°Simulation structural collapse due to earthquakes: model idealization, model calibration, and numerical solution algorithms,¡± Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Rhodes, Greece.

Hsu, T. T. C. [1997] ¡°Nonlinear analysis of membrane elements by fixed-angle softened-truss model,¡± ACI Structural Model 94(5), 483-492.

Ibarra, L. F. and Krawinkler, H. [2005] ¡°Global collapse of frame structures under seismic excitations,¡± Rep. No. TB 152, The John A. Blume Earthquake Engineering Center, Stanford University, Stanford, CA.

Ibarra, L. F., Medina, R. A. and Krawinkler, H. [2005] ¡°Hysteretic models that incorporate strength and stiffness deterioration,¡± Earthquake Engineering & Structural Dynamics 34(12), 1489-1511.

Kabeyasawa, T., Kabeyasawa, T., Matsumori, T., Kim, Y. and Kabeyasawa, T. [2007] ¡°3-D collapse tests and analyses of the three-story reinforced concrete buildings with flexible foundation,¡± Proceedings of the 2007 Structures Congress, Long Beach, CA.

Kim, Y., Kabeyasawa, T., Matsumori, T. and Kabeyasawa, T. [2012] ¡°Numerical study of a full-scale six-story reinforce concrete wall-frame structure tested at E-Defense,¡± Earthquake Engineering & Structural Dynamics 41: 1217-1239.

L¨¦geron, F., Paultre, P. and Mazars, J. [2005] ¡°Damage mechanics modeling of nonlinear seismic behavior of concrete structures,¡± Journal of Structural Engineering 131(6), 946-955.

Lignos, D. G., Chung, Y., Nagae, T. and Nakashima, M. [2011a] ¡°Numerical and experimental evaluation of seismic capacity of high-rise steel buildings subjected to long duration earthquakes,¡± Computers & Structures 89, 959-967.

Lignos, D. G., and Krawinkler, H. [2011] ¡°Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading,¡± Journal of Structural Engineering 137(11), 1291-1302.

Lignos, D. G., Krawinkler, H. and Whittaker, A. S. [2011b] ¡°Prediction and validation of sidesway collapse of two scale models of a 4-story steel moment frame,¡± Earthquake Engineering and Structural Dynamics 40 (7), 807-825.

Lignos, D. G. and Krawinkler, H. [2012] ¡°Development and utilization of structural component databases for performance-based earthquake engineering,¡± Journal of Structural Engineering 139(8), 1382-1394.

Lignos, D. G., Hikino, T., Matsuoka, Y. and Nakashima, M. [2013] ¡°Collapse assessment of steel moment frames based on E-Defense full-scale shake table collapse tests,¡± Journal of Structural Engineering 139 (1), 120-132.

Lu, X. Z., Ye, L. P., Ma, Y. H. and Tang, D. Y. [2012] ¡°Lessons from the collapse of typical RC frames in Xuankou school during the great Wenchuan earthquake,¡± Advances in Structural Engineering 15(1), 139-153.

Lu, X., Lu, X. Z., Guan, H. and Ye, L. P. [2013] ¡°Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes,¡± Earthquake Engineering & Structural Dynamics 42(5), 705-723.

Lynch, K. P., Rowe, K. L. and Liel, A. B. [2011] ¡°Seismic performance of reinforced concrete frame buildings in southern California,¡± Earthquake Spectra 27(2), 399-418.

Mander, J. B., Priestley, M. J. and Park, R. [1988] ¡°Theoretical stress-strain model for confined concrete,¡± Journal of Structural Engineering 114(8), 1804-1826.

Maruyama, K., Ramirez, H. and Jirsa, J. O. [1984] ¡°Short rectangular RC columns under bilateral load histories,¡± Journal of Structural Engineering 110(1), 120-137.

Mitra, N. and Lowes, L. N. [2007] ¡°Evaluation, calibration, and verification of a reinforced concrete beam¨Ccolumn joint model,¡± Journal of Structural Engineering 133(1), 105-120.

Moaveni, B., He, X. F., Conte, J. P. and Restrepo, J. I. [2010] ¡°Damage identification study of a seven-story full-scale building slice tested on the UCSD-NEES shake table,¡± Structural Safety 32, 347-356.

Otani, S. [1999] ¡°RC building damage statistics and SDF response with design seismic forces,¡± Earthquake Spectra 15(3), 485-501.

Panagiotakos, T. B. and Fardis, M. N. [2001] ¡°Deformations of reinforced concrete members at yielding and ulitmate,¡± ACI Journal 98 (2), 135-148.

Panagiotou, M., Restrepo, J. I. and Conte, J. P. [2011] ¡°Shake-table test of a full-scale 7-story building slice. Phase I: Rectangular wall,¡± Journal of Structural Engineering 137(6), 691-704.

Park, S. and Mosalam, K. M. [2013] ¡°Simulation of reinforced concrete frames with nonductile beam-column joints,¡± Earthquake Spectra 29(1), 233-257.

Perus, I., Biskinis, D., Fajfar, P., Fardis, M. N., Grammatikou, S., Krawinkler, H. and Lignos, D. G. [2014]. ¡°The series database of RC elements,¡± Second European Conference on Earthquake Engineering and Seismology, Istanbul.

Qiu, F. W., Li, W. F., Pan, P. and Qian, J. R. [2002] ¡°Experimental tests on reinforced concrete columns under biaxial quasi-static loading,¡± Engineering Structures 24, 419-428.

Saatcioglu, M., Alsiwat, J. M. and Ozcebe, G. [1992]. ¡°Hysteretic behavior of anchorage slip in R/C members.¡± Journal of Structural Engineering, 118(9), 2439¨C2458.

Scott, M. H. and Hamutçuoğlu, O. M. [2008] ¡°Numerically consistent regularization of force-based frame elements,¡± International Journal for Numerical Methods in Engineering 76(10), 1612-1631.

Spacone, E., Filippou, F. C. and Taucer, F. F. [1996] ¡°Fiber beam-column model for non-linear analysis of R/C frames: Part I. Formulation,¡± Earthquake Engineering & Structural Dynamics 25(7), 711-726.

Stevens, N. J., Uzumeri, S. M. and Collins, M. P. [1991] ¡°Reinforced-concrete subjected to reversed-cyclic shear experiments and constitutive model,¡± ACI Structural Journal 88(2), 135-146.

Swinbanks, D. [1995] ¡°Kobe Earthquake Shatters Faith in Engineers,¡± Nature 373(6512), 273.

Tang, D. Y. [2011] ¡°Experimental and theoretical study on seismic collapse resistance of RC frame structures with equal span,¡± Master Dissertation, Department of Civil Engineering, Tsinghua University, Beijing, China.

Tram, T. N. and Kasai, K. [2011] ¡°Dynamic analysis of a full-scale four-story steel building experimented to collapse by strong ground motions,¡± Proceeedings of 8^th CUEE conference, Tokyo, Japan.

Vecchio, F. J. and Collins, M. P. [1986] ¡°The modified compression field theory for reinforced concrete elements subjected to shear,¡± ACI Structural Journal 83(2), 219-231.

Wu, C. L., Kuo, W. W., Yang, Y. S., Hwang, S. J., Elwood, K. J., Loh, C. H. and Moehle, J. P. [2009] ¡°Collapse of a nonductile concrete frame: shaking table tests,¡± Earthquake Engineering & Structural Dynamics 38, 205-224.

Yavari, S., Elwood, K. J. and Wu, C. L. [2009] ¡°Collapse of a nonductile concrete frame: Evaluation of analytical models,¡± Earthquake Engineering & Structural Dynamics 38, 225-241.