7 Conclusion
In this work, the progressive collapse of a typical super-tall RC frame-core tube building
model, exposed to extreme fires, was simulated using the proposed analysis framework and numerical model. The primary conclusions demonstrated the main findings
of this study are given as follows. Firstly, when subjected to extreme fire loads, the progressive collapse may originate
in the fire-affected areas. However, due to the
large redundancy of the super-tall RC frame-core tube building, the progressive
collapse of the residual structure outside of the fire-affected areas can
be prevented via alternative load paths. Secondly, the progressive collapse of the super-tall building
analyzed was triggered by the flexural failure of the peripheral columns,
due to the outward push by the thermal expansion of the upper floors and the
inward contraction of the lower floors. The more stories subjected to fire, the greater the
possibility of progressive collapse. Finally, when multiple stories were subjected to fire,
the internal forces in the components were redistributed in the horizontal
and vertical directions through the Vierendeel truss mechanism, due to thermal
expansion deformation. In summary, the present work reveals the mechanisms of the fire-induced progressive
collapse of a typical RC super-tall building,
and provides an effective analysis framework for further study of the fire
safety of tall and super-tall RC buildings, in particular, in evaluating the
collapse behavior of all potential regions of such a building under fire.
Reference
[1]
American Society of Civil Engineers (2010).
Minimum design loads for buildings and other structures (ASCE7-10). Reston
[2]
Jiang AS (1994) The documentary of Zhuhai
"6.16" disastrous fire-induced collapse accident. Zhejiang Fire
7(5): 5-8 (in Chinese)
[3]
Lu XL (2007) Seismic theory and application
of complex high-rise structures. Science Press, Beijing. (in Chinese)
[4]
The Ministry
of Housing and Urban-Rural Development of the People¡¯s Republic of China (2010)
Technical specification for concrete structures of tall building (JGJ3-2010).
Beijing
[5]
Menzies J (2001) Learning from disaster. The
Struct Engineer 79(19): 14-15
[6]
Bratina S, Planinc I, Saje M, Turk G (2003) Non-linear fire-resistance analysis of reinforced concrete beams. Struct
Eng Mech 16(6): 695-712
[7]
Bisby L A, Green M F, Kodur VKR (2005) Modeling
the behavior of fiber reinforced polymer-confined concrete columns exposed
to fire. J Compos Constr 9(1): 15-24
[8]
Mostafaei H (2013) Hybrid fire testing for
assessing performance of structures in fire-Application. Fire Saf J 56(2):
30-38
[9]
Mostafaei H (2013) Hybrid fire testing for
assessing performance of structures in fire-Methodology. Fire Saf J 58(5):
170-179
[10]
Wang Y C (2000) An analysis of the global structural behavior of the
Cardington steel-framed building during the two BRE fire tests. Eng Struct
22(5): 401-412
[11]
Sun R, Huang ZH, Burgess IW (2012) Progressive collapse analysis of
steel structures under fire conditions. Eng Struct 34(2):400¨C413
[12]
Kotsovinos P, Usmani A (2013) The World Trade Center 9/11 disaster
and progressive collapse of tall buildings. Fire Tech 49(3): 741-765
[13]
Lange D, Röben C, Usmani A (2012) Tall building collapse mechanisms
initiated by fire: mechanisms and design methodology. Eng Struct 36(3): 90-103
[14]
Fletcher IA (2009) Tall concrete buildings subjected to vertically
moving fires: a case study approach. The University of Edinburgh, Edinburgh.
[15]
Gentili F, Giuliani L, Bontempi F (2013). Structural
response of steel high rise buildings to fire: system characteristics and
failure mechanisms. J Struct Fir Eng 4(1): 9-26
[16]
Rackauskaite E, El-Rimawi J (2015). A study on the effect of compartment
fires on the behaviour of multi-storey steel framed structures. Fire Tech
51(4): 867-886
[17]
Jiang J, Li GQ, Usmani A (2015). Effect of bracing systems on fire-induced
progressive collapse of steel structures using OpenSees. Fire Tech 51(5):
1249-1273
[18]
Flint G, Lamont S, Lane B, Sarrazi H, Lim L, Rini D, Roben C (2013).
Recent lessons learned in structural fire engineering for composite steel
structures. Fire Tech 49(3): 767-792
[19]
Li Y, Lu XZ, Guan H, Ying MJ, Yan WM (2015) A case study on a fire-induced
collapse accident of a reinforced concrete frame-supported masonry structure. Fire Tech.
DOI: 10.1007/s10694-015-0491-0.
[20]
Lu X, Lu XZ, Guan H, Ye LP (2013) Collapse simulation
of reinforced concrete high-rise building induced by extreme earthquakes.
Earthq Eng Struct Dyn 42(5): 705-723
[21]
Qian K, Li B (2015) Research advances in design of structures to resist
progressive collapse. J Perform Constr Fac, ASCE DOI: 10.1061/(ASCE)CF.1943-5509.0000698
, B4014007
[22]
Miao ZW, Ye LP, Guan H, Lu XZ (2011) Evaluation
of modal and traditional pushover analyses in frame-shear-wall structures.
Adv Struct Eng 14(5): 815-836
[23]
Guan H, Loo YC (1997) Flexural and shear failure analysis of reinforced
concrete slabs and flat plates. Adv Struct Eng 1(1):71-85
[24]
MSC Software Corp (2005) MSC.Marc Volume A: Theory and User Information
[25]
Lie TT, Irwin RJ (1993) Method to calculate the fire resistance of
reinforced concrete columns with rectangular cross section. ACI Struct J 90(1):
52-60
[26]
George SJ, Tian Y (2012) Structural performance of reinforced concrete
flat plate buildings subjected to fire. Int J Concrete Struct Mater 6(2):
111-121
[27]
Shi XD, Tan TH, Tan KH (2002) Concrete constitutive relationships under
different stress-temperature paths. J Struct Eng, ASCE, 128(12):1511-1518
[28]
Guo ZH, Shi XD (2003) Behavior
of reinforced concrete at elevated temperature and its calculation. Tsinghua
University Press, Beijing (in Chinese)
[29]
Lu XZ, Li MK, Guan H, Lu X, Ye LP (2015) A comparative case study on
seismic design of tall RC frame-core tube structures in China and USA. Struct
Des Tall Spec, 24(9): 687-702
[30]
The Ministry of Housing and Urban-Rural
Development of the People¡¯s Republic of China (2010) Code
for seismic design of buildings (GB50011-2010), Beijing
[31]
Moehle J, Bozorgnia Y, Jayaram N, et al. (2011) Case studies of the
seismic performance of tall buildings designed by alternative means. Pacific
Earthquake Engineering Research Center, Berkeley, California
[32]
The Ministry of Construction of the People¡¯s Republic of China (2006)
Code of design on building fire protection and prevention (GB50016-2006).
Beijing
[33]
Commission of European Communities (2004)
EN1992-1-2: Eurocode 2: design of concrete structures. Part 1¨C2:general rules¡ªstructural
fire design. Brussels
[34]
National Fire Protection Association (2008) NFPA 921: guide for fire
and explosion investigations. National Fire Protection Association. Massachusetts
[35]
China Association for Engineering Construction Standardization (2014)
Code for anti-collapse design of building structures (CECS 392). Beijing (in
Chinese)
[36]
United States General Services Administration (2003) Progressive collapse
analysis and design guidelines for new federal office buildings and major
modernization projects. Washington D.C
[37]
Kono M (2005) The Madrid city Windsor building fire inspection report.
The Madrid city Windsor building fire investigation committee (In Japanese)
[38]
McAllister T, MacNeill R, Erbay O, et al. (2011)
Analysis of structural response of WTC 7 to fire and sequential failures leading
to collapse. J Struct Eng, ASCE 138(1): 109-117
[39]
International Standard Organization (1999) International standard ISO
834-1: fire resistance tests¡ªelements of building construction¡ªPart 1: general
requirements. Geneva
[40]
The Ministry of Public Security of the People¡¯s
Republic of China. (2005) Code for fire protection design of tall buildings
(GB50045-95). Beijing
[41]
MSC.Software Corporation (2007) MSC.Marc Volume B: Element Library,
California
[42]
American Society for Testing and Materials (2008) ASTM E119: Standard
test methods for fire test of building construction and materials. Pennsylvania
[43]
Lin TD, Gustaferro AH, Abrams MS (1981) Fire
endurance of continuous reinforced concrete beams. Portland Cement Association,
1981
[44]
Lim LCS, Wade CA (2002) Experimental fire tests of two-way concrete
slabs. University of Canterbury, Canterbury
Appendix A
1 Material constitutive laws
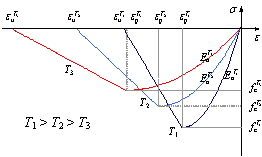
It is well known that the strains on concrete at high temperatures are
made up of 4 components: stress strain (¦Å¦Ò), thermal expansion
strain (¦Åth), thermal creep strain (¦Åcr),
and thermal transient strain (¦Åtr) [27]. The behaviors of
concrete subject to these four strain components are simulated using the models
proposed by Guo and Shi [27, 28]. The stress-strain (¦Å¦Ò)
curve of concrete is shown in Figure A.1. Specifically, for concrete layers
in multi-layer shell elements, the elasto-plastic-creep constitutive model
provided by MSC.Marc [41] is adopted. The relationships between the equivalent
stress and the stress strain (¦Å¦Ò) at different temperatures
are inputted into MSC.Marc by defining a series of stress-strain curves at
different temperatures. The thermal expansion strain (¦Åth)
is simulated by defining a thermal expansion coefficient curve at different
temperatures in MSC.Marc. The deformation of concrete due to the thermal creep
strain (¦Åcr) and thermal transient strain (¦Åtr)
are simulated by programming the user subroutine CRPLAW in MSC.Marc. For the
concrete fibers in the fiber beam elements, the behavior of concrete is defined
using the subroutine UBEAM, following the previous work of Li et al. [19].
|
|
|
|
(a) Compression
|
(b) Tension
|
|
Figure A.1 Temperature-dependent stress-strain curve
of concrete
|
Note: T1, T2 and T3
are the temperatures of concrete; fTc, ¦ÅTp, ETo and ¦ÅTu are the peak compression strength and
corresponding strain, initial elastic modulus and ultimate compression strain
of concrete under the temperature T, respectively; fTt,
¦ÅTtcr and ¦ÅTtu are the tension strength, cracking strain
and ultimate tension strain of concrete under the temperature T,
respectively; a is
the cracking factor, set to 0.5.
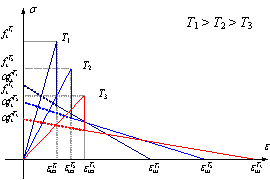
The constitutive model of steel is much simpler. The
constitutive law of steel accounting for high temperature effects proposed
by Guo and Shi [28] is adopted and implemented in MSC.Marc according to the
work of Li et al. [19]. The stress-strain curve of steel is shown in Figure
A.2.
|
|
|
Figure A.2 Temperature-dependent stress-strain curve
of steel
|
Note: T1, T2 and T3
are the temperatures of steel; fTy, fTu, ETs, ¦ÅTy and ¦ÅTsu are the yield strength, ultimate strength,
elastic modulus, yield strain and ultimate strain of steel under the temperature
T,
respectively
2 Elemental failure criteria
During
the collapse process, the structural components either crack or crush to small
fragments. This phenomenon is simulated with the elemental deactivation technology.
When a specified elemental-failure criterion is reached, the element will
be ¡°deactivated¡± and be removed from the FE model.
In
this study, if the principal compressive strain in a layer/fiber exceeds the
ultimate strain of concrete (i.e., the softening branch of the concrete approaching
zero), or the principal tensile strain exceeds the rupture strain of steel,
the stress and stiffness of this layer/fiber are deactivated. Thus, this layer/fiber
no longer contributes to the computation of the entire structure. If all the
layers of a shell element, or all the fibers in a fiber beam element are deactivated,
the element is considered fully deactivated from the model [24]. The ultimate
strains of steel and concrete at high temperatures suggested by Guo and Shi
[28] are used in this work.
Appendix B
1 Validation using RC column test results
Lie et al. [25] performed a series of fire tests of full-scale RC columns.
In this study, a test specimen with a sectional size of 305 ¡Á 305 mm is selected
to validate the developed numerical model (Figure B.1). This column is fixed
at both ends, and a constant axial load is applied on the column throughout
the heating process. The temperature in the furnace is controlled according
to the ASTM E119 standard heating curve [42]. The temperature fields measured
in the test and predicted by MSC.Marc are shown in Figure B.1b. A good agreement
is obtained. Some differences exist between the predicted and measured temperatures
during the earlier stage of fire exposure (0 - 50 min). Such a difference
is also found by Lie et al. [25] which is due to the migration of moisture.
Note that at a later stage, good agreement between the calculated and measured
temperatures is obtained, which is an important stage when predicting fire
resistance.
|
![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image069.gif)
|
|
(a) Test specimen (unit: mm)
|
|
![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image071.gif)
|
![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image073.gif)
|
|
(b) Comparison of temperature-time relationships
|
(c) Comparison of deformation-time relationships
|
|
Figure B.1 Validation using the RC column tested by
Lie et al. [25].
|
The axial displacements measured in the test
and predicted by MSC.Marc are shown in Figure B.1c. Because the predicted temperature is lower than
the experimental values during the initial stage, the simulated deformation
is also smaller. At a later stage, the predicted deformation agrees well with
the test results. Therefore, the developed model can be used to analyze the
fire-induced failure of columns. The analyses using 105% and 95% of the material
strength are also conducted to demonstrate the effect of material uncertainty
on the structural response of the RC column exposed to fire. It can be seen
from Figure B.1c that the material strength certainly influences the deformation
of the column after 40 min. At this time, a large proportion of the column
section is under high temperature. The material degradation significantly
increases the actual axial load ratio, which consequently influences the mechanical
response of the column in fire.
2 Validation using RC beam test results
Lin et al. [43] performed a series of fire-resistance tests of RC beams.
One of the beams is selected to validate the developed numerical model.
The boundary conditions, geometric dimensions
and reinforcement information are shown in Figure B.2a. The diameter and yield
strength of the steel bar were 19 mm and 435.8 MPa, respectively. The cylinder
compressive strength of the concrete was 29.46 MPa. In this test, the bottom
and both sides of the beam were exposed to an ASTM E119 standard fire [42].
The predicted temperature fields
using MSC.Marc are shown in Figure B.2b, which is consistent with the test
results. The predicted
deformation is shown in Figure B.2c. During the early stage of heating, the
simulated result is slightly smaller than the test results. However, the simulation at and beyond 30 min agrees well with the test results, which
are significant for a collapse simulation. Note that no measured data are
available for the test after 80 min of heating due to the excessively large
deformation of the beam. However, the numerical simulation can trace the deformation
of the components throughout the failure process.
3 Validation using RC slab test results
Lin and Wade [44] tested a series of two-way RC slabs. Two specimens
(DH12 and D147) are simulated herein with identical sizes and loads (Figure
B.3a). However, Specimen D147 had a smaller reinforcement
ratio than Specimen DH12. A four-edge simple-supported boundary condition
was applied to the specimen during the test. The slabs were heated at the
bottom in the furnace. A constant distributed load was applied to the specimens
throughout the heating process.
|
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image081.gif)
|
|
(a) Test specimen (unit: mm)
|
|
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image083.gif)
|
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image085.gif)
|
|
(b) Comparison of temperature-time relationships
|
(c) Comparison of deformation-time relationships
|
|
Figure B.3 Validation using the simply supported two-way RC slabs
tested by Lin et al. [44].
|
The multi-layer shell element model is used to simulate
the fire temperature distribution. The simulated temperature distribution
agrees well with the test results, as shown in Figure B.3b. Furthermore, the
predicted deformation is consistent with the test (Figure B.3c). Note that
some discrepancies exist between the test results and the predicted deformation
of Specimen D147 when the deformation is greater than 186 mm. This is because
such a large deformation is beyond the capabilities of the test instrument.
However, the numerical simulation
is capable of predicting the collapse behavior under large deformations. Therefore,
the comparison of these two specimens further validates the accuracy of the
developed model. The analysis also indicates that the 5% variation of the
material strength has little effect on the mechanics response of the RC slabs.
This is because the slabs exhibit the tensile membrane action under fire in
which the two-way load transferring mechanism dominates the deformation of
the slabs.
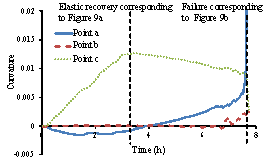
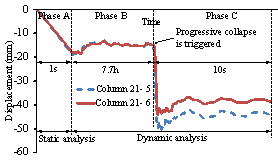
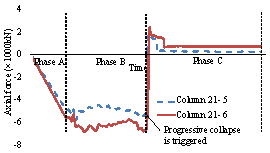
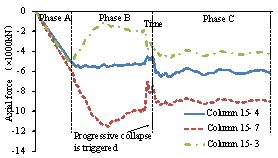
List of Figures and Tables:
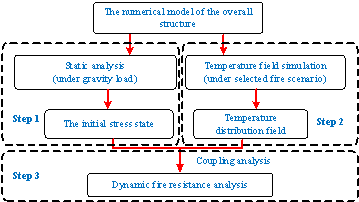
Figure 1 Framework for simulating the fire-induced
progressive collapse of super-tall RC buildings
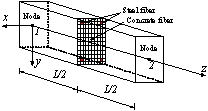
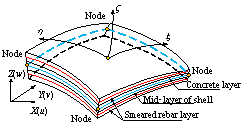
Figure 2 Fiber
beam and multi-layer shell elements
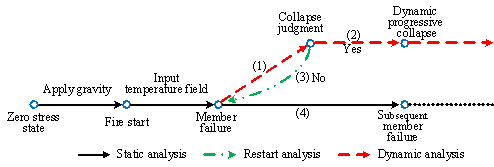
Figure 3 Analysis procedure
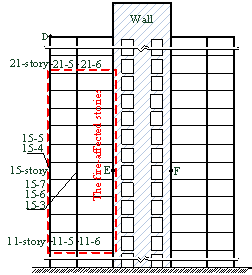
Figure 4 Structural
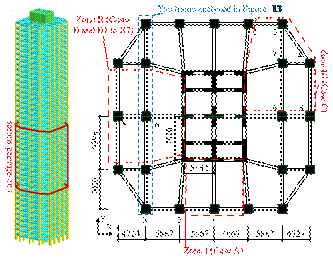
arrangement and position of the fire-affected area (unit: mm)
Figure 5 Failure modes of Cases A and
C
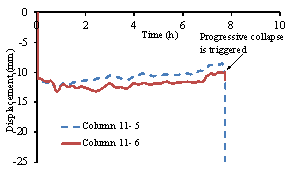
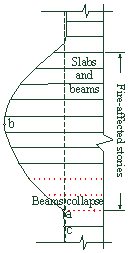
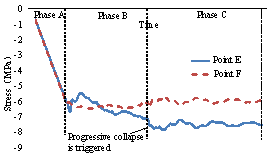
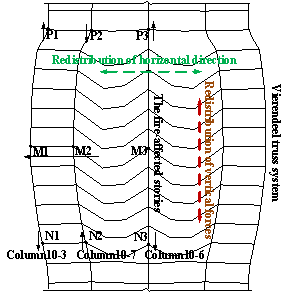
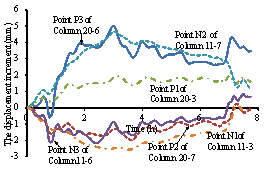
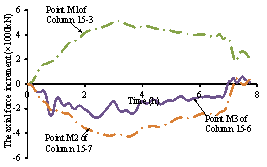
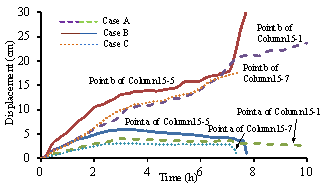
Figure 6 Positions of the key points
and key components
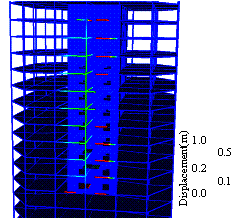
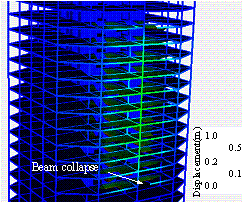
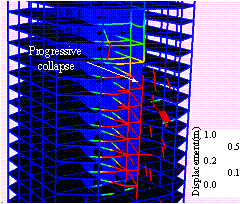
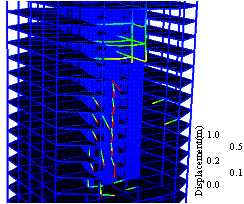
Figure 7 Simulated progressive collapse
process (unit: m)
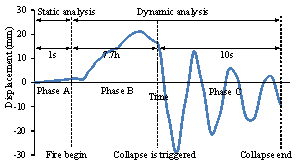
Figure 8 Time history of the horizontal
displacement of Point D
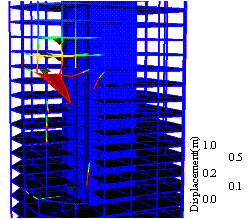
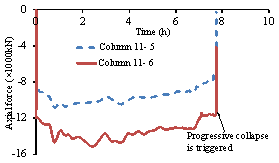
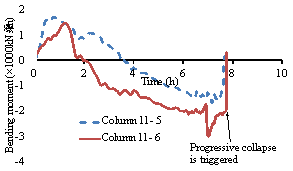
Figure 9 Time history responses of the
columns
Figure 10 Deformation of the column (deformation
magnification scale 1:40)
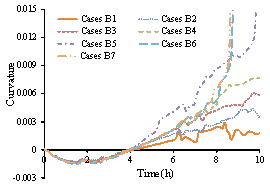
Figure 11 Time history of the curvatures of
the column
Figure 12 Time history of the surrounding
structures
Figure 13 Force redistribution in the structure
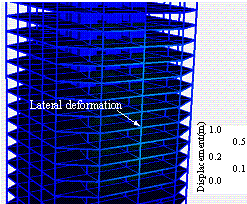
Figure 14 Lateral displacement of fire-affected
columns
Figure 15 Time history of the curvature of
Point a for different cases
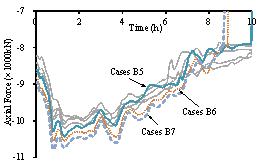
Figure 16 Time history of the axial force
of Column 15-5 for different cases (the gray line represents cases B1-B4)
Figure A.1 Temperature-dependent stress-strain
curve of concrete
Figure A.2 Temperature-dependent stress-strain
curve of steel
Figure B.1 Validation
using the RC column tested by Lie et al. [25]
Figure B.2 Validation using the RC beam tested
by Lin et al. [43]
Figure B.3 Validation using the simply supported
two-way RC slabs tested by Lin et al. [44]
Table 1 Examples
of fire-induced collapse incidents of RC structures in China during the
last 25 years
Table 2 Simulation cases
|






![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image069.gif)
![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image071.gif)
![Figure B.1 Validation using the RC column tested by Lie et al. [25].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image073.gif)
![Figure B.2 Validation using the RC beam tested by Lin et al. [43].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image075.gif)
![Figure B.2 Validation using the RC beam tested by Lin et al. [43].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image077.gif)
![Figure B.2 Validation using the RC beam tested by Lin et al. [43].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image079.gif)
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image081.gif)
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image083.gif)
![Figure B.3 Validation using the simply supported two-way RC slabs tested by Lin et al. [44].](./2016-FT-Super-tall_Fire_Progressive_Collapse.files/image085.gif)