|
6.
Assessment of The Design Parameters in The Existing Codes and Validation of
The Collapse Resistance of RC Frames
The progressive collapse resistance of RC
frames can be evaluated via a nonlinear static pushdown analysis. Given that
the collapse process exhibits a strong dynamic effect, a maximum structural
resistance that is larger than the design vertical load must be attained in
order to prevent progressive collapse from happening. In other words, the maximum
relative resistance qmax/g must be larger than 1.0.
Based on this consideration, the resistance of the RC frames is further validated
using the nonlinear dynamic alternative load path method (DoD, 2010; Li et
al., 2011).
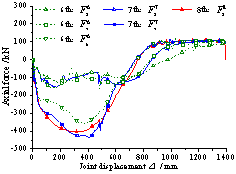
For the two models, Figure
9 presents the maximum relative resistance qmax/g versus
the ductility ratio m for a total of 32 column removal scenarios.
For the portion of the frames undergoing large deformations, m is defined as the ratio
of the joint displacement corresponding to the maximum relative resistance to
the yield displacement (Pujol and Smith-Pardo, 2009; Tsai, 2010). The expression
qmax/g refers to as the peak value of each resistance
curve presented in Figures 3 and 7. In Figure 9, the hollow and solid marks
demote collapse and non-collapse scenarios, respectively, based on the outcome
of the nonlinear dynamic alternative load path analysis. It is evident that
a collapse can be prevented when qmax/g of the RC frames
is larger than 1.236. In addition, the minimum values of qmax/g
to prevent collapse for the corner, short edge, long edge and internal
column removal scenarios are 1.296, 1.327, 1.236 and 1.280, respectively. The
factors for different column removal scenarios are very close because the ductility
ratios of RC beams designed by the Chinese codes (MOHURD, 2010a; 2010b) are
similar (varying from 3 to 4). This can also be confirmed by the existing
theoretical study (Li et al., 2014a) that the dynamic amplification factor
(i.e. the required values of qmax/g, for regular RC
frame structures) equals 1.33 when the structural ductility ratio equals 4.0.

Figure 9 Design parameters
in the existing codes
To facilitate practical designs,
the linear static and nonlinear static methods are recommended by the existing
codes as the simplified approaches to calculate the progressive collapse resistance.
In these methods, the resistance directly obtained from the linear static and
nonlinear static analyses, which is equivalent to the applied vertical load
g in this study, is further corrected using the dynamic amplification
factor (DAF) and the demand capacity ratio (DCR), respectively, to account for
the dynamic and nonlinear effects. In the GSA guideline (GSA, 2003), the required
equivalent values of qmax/g, i.e. DAF/DCR, are 1.0
and 1.33, respectively, for typical and atypical structural configurations (see
Figure 9). The analysis results presented in Figure 9 demonstrate that the GSA
requirement for atypical structures is adequately met whilst that for typical
structures cannot be met which would lead to unsafe designs. This is because
the dynamic effect is consistently neglected (qmax/g
=1).
In the DoD2005 guideline (DoD,
2005), a DAF of 2.0, considering the nonlinear effect, is used for the linear
and nonlinear static analyses in which the required equivalent value of qmax/g
is also 2.0. The validation shown in Figure 9 demonstrates that the design parameter
is over conservative because the structures satisfying such requirement will
exhibit elastic behavior after the column removal.
In the DoD2010 guideline (DoD,
2005), different values of DAFs are given for the linear and nonlinear static
analyses. An expression of the DAF for nonlinear static analyses is regulated
by Eq.(1) which is presented by the solid line in Figure 9.
| |
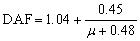
|
(1)
|
It can be seen that the GSA2003 requirement
is higher than that for typical structures but is still unsafe for the RC frames
discussed herein. Model A and Model B will collapse under three and two column
removal scenarios, respectively. This is because Eq.(1) is obtained from the
numerical analyses of typical planar 3-storey and 10-storey frames, from which
the results cannot accurately describe the nonlinear dynamic effect of all types
of frame buildings (Marchand et al., 2009).
On the other hand, two DAFs
are regulated for linear static analyses in the DoD2010 guideline. The force-controlled
DAF is 2.0 for fragile structures (i.e. m=1). Although rational, this DAF is only suitable for the elastic response when
no structural ductility can be considered. The deformation-controlled DAF, on
the other hand, is much larger than 2.0. This is because it is obtained based
on the equal deformation demand in which the same deformation is applied to
the RC frames in both linear static and dynamic analyses (Marchand et al.,
2009). This is however not the focus of this study in which the nonlinear static
method is used and the equal deformation demand is not required.
7.
Discussion and Concluding Remarks
In this study, the progressive collapse behavior
of an RC frame with two different seismic design intensities is analyzed using
the nonlinear static pushdown method. The following conclusions are drawn and
recommendations for future seismic designs against progressive collapse are
given:
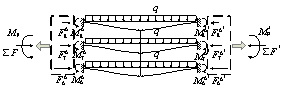
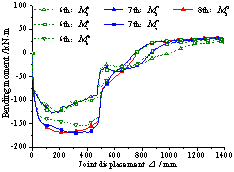
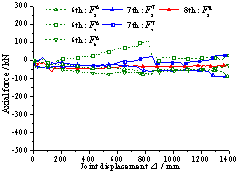
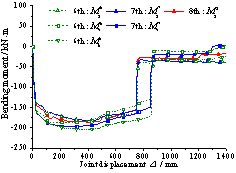
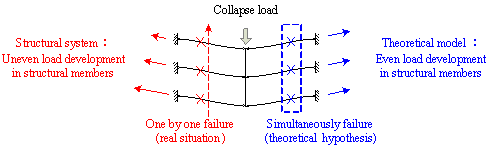
(1) Vierendeel action leads
to uneven internal forces in the beams of different stories. This may result in the beams fail successively
from one floor to the other in a frame system, which differs from the theoretical
assumption in that the beams are damaged simultaneously on different floors.
This action also weakens the compressive arch mechanism of the beams,
and therefore reduces the relative collapse resistance of RC frames under the
beam mechanism. This is particularly true for frames with more stories. In view
of this, considering only the pure flexural strength of the beams under the
beam mechanism is a conservative and rational approach for design purposes.
Furthermore, the catenary action is the prototype model of the tie force method
in existing design codes and is assumed to be able to develop fully on all stories.
However, Vierendeel action delays the catenary action on upper stories thereby
reducing the progressive collapse resistance. Neglecting this effect will result
in insufficient resistance to prevent progressive collapse. Hence, this phenomenon
is recommended to be considered in future improvement of the tie force method.
(2) Seismic design significantly
enhances the progressive collapse resistance of RC frames under the beam mechanism.
However, such enhancement is not as significant under the catenary mechanism.
This is because the axial tension of the catenary mechanism is provided by continuous
reinforcement in the beam. Seismic design consideration significantly increases
the reinforcement amount in the beam ends however such an increase at the mid-span
is small. Hence, it is suggested that the progressive collapse resistance can
be improved by extending and connecting a portion of the seismic reinforcement
which is proven very effective and economical for RC frames constructed in the
seismic areas. In addition, seismic design significantly enhances the progressive
collapse resistance of the bottom stories. However, such enhancement is limited
for the top stories. Thus, the top stories may become the weakest location in
progressive collapse designs. This is a very important and useful finding, because
more attention is paid to the bottom stories of a structure in the existing
design specifications. It is therefore recommended to specifically examine the
progressive collapse resistance of the top stories of RC frames to ensure a
safe design of the entire structure.
(3) Based on the RC frames presented
in this study, the validation demonstrates that the GSA simplified static method
for atypical structures provides adequate resistance to prevent progressive
collapse; whereas that for typical structures is inadequate due to the absence
of dynamic effects which would result in unsafe designs. Furthermore, the nonlinear
static analysis specified in DoD2010 also leads to unsafe designs for the RC
frames concerned and further investigations in this area are needed.
Acknowledgement
The authors are grateful for the financial
support received from the National Basic Research Program of China (No. 2012CB719703),
the National Science Foundation of China (No. 51578018, 51208011) and the Australian
Research Council through an ARC Discovery Project (DP150100606).
References
Alashker, Y., El-Tawil, S. and Sadek, F. (2010). ¡°Progressive
collapse resistance of steel-concrete composite floors¡±, Journal of Structural Engineering, ASCE,
Vol. 136, No. 10, pp. 1187-1196.
American Society of Civil Engineers (ASCE) (2005). Minimum Design
Loads for Buildings and Other Structures, Standard ASCE/SEI 7-05, Reston.
American Society of Civil Engineers (ASCE) (2007). Seismic Rehabilitation of Existing Buildings,
Standard ASCE/SEI 41-06. Reston.
Department of Defense (DoD) (2005). Unified Facilities Criteria
(UFC): Design of Buildings to Resist Progressive Collapse. Washington
(DC).
Department of Defense (DoD) (2010). Unified Facilities Criteria
(UFC): Design of Buildings to Resist Progressive Collapse. Washington
(DC).
Fu, F. (2009). ¡°Progressive
collapse analysis of high-rise building with 3-D finite element modeling method¡±, Journal of Constructional
Steel Research, Vol. 65, No. 6, pp.
1269-1278.
Galal, K. and El-Sawy, T. (2010). ¡°Effect of retrofit strategies
on mitigating progressive collapse of steel frame structures¡±, Journal of Constructional
Steel Research, Vol. 66, No. 4, pp.
520-531.
General Service Administration (GSA). (2003). Progressive Collapse Analysis and Design Guidelines for New Federal Office
Buildings and Major Modernization
Projects, Washington (DC).
Huang, Y. (2009). ¡°Simulating the inelastic
seismic behavior of steel
braced frames including the effects of low-cycle
fatigue¡±, PhD thesis, University of California, Berkeley, Berkeley.
Huang, Z., Li, B. and Sengupta, P. (2014) ¡°Reliability
assessment of damaged RC moment-resisting frame against progressive collapse
under dynamic loading conditions¡±, Advances in Structural
Engineering, Vol. 17, No. 2, pp. 211-232.
International Organization for Standardization (ISO) (1999). Fire Resistance Tests-Elements of Building Construction, Part 1: General Requirements (ISO-834), Geneva.
Jiang, J., Li, G.Q. and Usmani, A. (2014) ¡°Progressive
Collapse Mechanisms of Steel Frames Exposed to Fire¡±, Advances in Structural Engineering, Vol. 17, No.
3, pp. 381-398.
Jiang,
Q., Lu. X.Z., Guan, H. and Ye, X. (2014). ¡°Shaking table model test and FE analysis
of a reinforced concrete mega-frame structure with tuned mass dampers¡±, The
Structural Design of Tall and Special Buildings, doi: 10.1002/tal.1150.
Kokot, S., Anthoine, A., Negro, P. and Solomos,
G. (2012). ¡°Static and dynamic analysis of a reinforced concrete flat slab frame
building for progressive collapse¡±, Engineering
Structures, Vol. 40, No. 7, pp. 205-217.
Kwasniewski, J. (2010). ¡°Nonlinear dynamic simulations of progressive collapse
for a multistory building¡±. Engineering Structures, Vol. 32, No. 5, pp.
1223-1235.
Khandelwal, K. and El-Tawil, S.
(2008). ¡°Assessment of progressive collapse
residual capacity using pushdown analysis¡±, Proceedings of the
2008 ASCE Structures Congress, ASCE.
Khandelwal, K., El-Tawil, S. and Sadek, F. (2009). ¡°Progressive
collapse analysis of seismically designed steel braced frames¡±, Journal of Constructional
Steel Research, Vol. 65, No. 3, pp.
699-708.
Kim, T., Kim, J. and Park, J. (2009). ¡°Investigation
of progressive collapse-resisting capability of steel moment frames using push-down
analysis¡±, Journal
of Performance of Constructed Facilities, ASCE.
Vol. 23, No. 9, pp.
327-335.
Kim, J., Park, J. and Lee, T. (2011). ¡°Sensitivity
analysis of steel buildings subjected to column loss¡±, Engineering Structures, Vol. 33, No. 2, pp.
421-432.
Luccioni, B.M., Ambrosini, R.D. and Danesi, R.F. (2004). ¡°Analysis of building collapse under blast
loads¡±, Engineering Structures, Vol. 26, No. 1, pp. 63-71.
Lu, X., Lu, X.Z., Guan, H. and Ye, L.P. (2013). ¡°Collapse simulation of reinforced concrete high-rise
building induced by extreme earthquakes¡±,
Earthquake Engineering & Structural Dynamics, Vol. 42, No. 5, pp. 705-723.
Li, Y., Lu, X.Z.,
Guan, H. and Ye, L.P. (2011). ¡°An improved
tie force method for progressive collapse resistance design of reinforced concrete
frame structures¡±, Engineering
Structures, Vol. 33, No. 10, pp. 2931-2942.
Li,
Y., Lu, X.Z., Guan, H. and Ye, L.P. (2014a). ¡°An energy-based assessment on
dynamic amplification factor for linear static analysis in progressive collapse
design of ductile RC frame structures¡±, Advances in Structural Engineering,
Vol. 17, No. 8, pp. 1217-1225.
Li,
Y., Lu, X.Z., Guan, H. and Ye, L.P. (2014b). ¡°Progressive collapse resistance
demand of RC frames under catenary mechanism¡±, ACI Structural Journal,
Vol. 111, No. 5, pp. 1225-1234.
Matthews, T., Elwood, K.J. and
Hwang, S. (2007). ¡°Explosive testing
to evaluate dynamic amplification during gravity load redistribution for reinforced
concrete frames¡±, Proceedings of the 2007 ASCE Structures
Congress, ASCE.
Marchand, K.A., McKay, A.E. and Stevens, D.J. (2009).
¡°Development and application of linear and non-linear static approaches in UFC
4-023-03¡±, Proceedings of the 2009 ASCE Structures Congress, ASCE.
Pujol, S. and Smith-Pardo, J.P. (2009). ¡°A new perspective
on the effects of abrupt column removal¡±, Engineering
Structures, Vol. 31, No. 4, pp.
869-874.
Qian, K. and Li, B. (2012a). ¡°Slab effects on the
response of reinforced concrete substructures after the loss of a corner column¡±,
ACI Structural Jouranl, Vol. 109, No. 6, pp. 845-855.
Qian, K. and Li, B. (2012b). ¡°Dynamic performance
of RC beam-column substructures under the scenario of the loss of a corner column-Experimental results¡±,
Engineering
Structures, Vol. 34, No. 9, pp.
154-167.
Rahai, A., Asghshahr, M.S., Banazedeh, M. and Kazem,
H. (2013) ¡°Progressive collapse assessment of RC structures under instantaneous
and gradual removal of columns¡±, Advances
in Structural Engineering, Vol. 16, No.
10, pp. 1671-1682.
Ren, P.Q.,
Li, Y., Guan,
H. and Lu, X.Z. (2014). ¡°Progressive collapse resistance
of two typical high-rise RC frame shear wall structures¡±, Journal of Performance
of Constructed Facilities, ASCE.
doi: 10.1061/(ASCE)CF.1943-5509.0000593
Sadek, F., Main, J.A.,
Lew, H.S. and Bao, Y. (2011). ¡°Testing and analysis of
steel and concrete beam-column assemblies under a column removal scenario¡±,
Journal of
Structural Engineering, ASCE. Vol. 137, No.
9, pp. 881-892.
Sasani, M., Bazan, M. and Sagiroglu, S. (2007). ¡°Experimental
and analytical progressive collapse evaluation of actual reinforced concrete
structure¡±, ACI Structural Jouranl, Vol. 104, No. 6, pp.
731-739.
Sasani, M. and Sagiroglu, S. (2010). ¡°Gravity load redistribution and progressive
collapse resistance of 20-story reinforced concrete structure following loss
of interior column¡±, ACI Structural Jouranl, Vol. 107, No.
6, pp. 636-644.
Sasani, M., Kazemi, A.,
Sagiroglu, S. and Forest, S. (2011). ¡°Progressive collapse resistance
of an actual 11-story structure subjected to severe initial damage¡±,
Journal of
Structural Engineering, ASCE. Vol. 137, No. 9, pp.
893-902.
Starossek, U. (2007). ¡°Typology of progressive
collapse¡±, Engineering Structures, Vol. 29, No. 9, pp. 2302-2307.
Song, B.I. and Sezen, H. (2009). ¡°Evaluation of
an existing steel frame building against progressive collapse¡±, Proceedings
of the 2009 ASCE Structures Congress, ASCE.
Su, Y., Tian, T. and Song, X. (2009). ¡°Progressive
collapse resistance of axially-restrained frame beams¡±, ACI Structural Jouranl, Vol. 106,
No. 5, pp. 600-607.
The Ministry of Housing and Urban-Rural Development of the People¡¯s Republic of China (MOHURD).
(2010a). Code for Design of Concrete Structures, GB50010-2010,
Beijing.
The Ministry of Housing and Urban-Rural Development of the People¡¯s Republic of China (MOHURD).
(2010b). Code for Seismic
Design of Buildings, GB50011-2010, Beijing.
Tsai, M.H. (2010). ¡°An analytical methodology for
the dynamic amplification factor in progressive collapse evaluation of building
structures¡±, Mechanics Research Communications, Vol. 37, No. 1, pp. 61-66.
Vamvatsikos, D. and Cornell, C.A. (2002) ¡°Incremental
dynamic analysis¡±, Earthquake Engineering & Structural Dynamics,
Vol. 31, No. 3, pp. 491-514.
Yap, S.L. and Li, B. (2011). ¡°Experimental investigation of reinforced concrete
exterior beam-column subassemblages for progressive collapse¡±, ACI Structural Jouranl, Vol. 108,
No. 5, pp. 542-552.
Yi, W.J., He, Q.F.,
Xiao, Y. and Kunnath, S.K. (2008).
¡°Experimental study on progressive collapse-resistant behavior
of reinforced concrete frame structures¡±, ACI Structural Jouranl, Vol. 105,
No. 4, pp. 433-439.
Yi, W.J., Kunnath,
S.K., Zhang, F.Z. and Xiao, Y. (2011). ¡°Large-scale experimental evaluation of building system
response to sudden column removal¡±. Proceedings
of the 2011 ASCE Structures Congress
List
of Tables
Table 1.
Parameters of the structural
members in the RC frame
Table 2.
Design loads and action
on the RC frame
List
of Figures
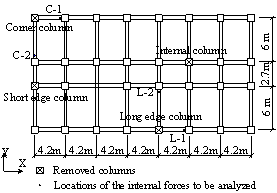
Figure 1.
Plan view of the RC
frame
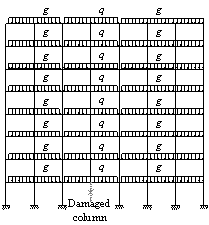
Figure 2.
Load pattern for pushdown
analysis of the RC frames
Figure 3.
Progressive collapse
resistance curves for Model A
Figure 4.
Combined action of
beams on different stories (beam L-1)
Figure 5.
Combined action of
beams on different stories (beam L-2)
Figure 6.
Structural vulnerability
due to uneven internal force development
Figure 7.
Progressive collapse
resistance curves for Model B
Figure 8.
Comparison between
the progressive collapse resistance of Model A and Model B
Figure 9.
Design parameters
in the existing codes
*
Corresponding author, Email: Luxz@tsinghua.edu.cn, Phone (Fax): +86-10-62795364
|