Application of the FEMA-P58 Methodology for Regional Earthquake Loss Prediction

Xiang Zeng ^a, Xinzheng Lu ^a, T.Y. Yang ^b and Zhen Xu ^c

a Department of Civil Engineering, Tsinghua University, Beijing, P.R. China

b Department of Civil Engineering, University of British Columbia, Vancouver, Canada

c School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing, P.R. China

Natural Hazards, 2016, 83(1): 177-192. .

Download Full Text

Abstract: Earthquake-induced building collapses and casualties have been effectively controlled in the last two decades. However, earthquake-induced economic losses have continued to rise. Following the objective and procedure of next-generation performance-based seismic design, the economic loss prediction method proposed by FEMA-P58 is extended to regional earthquake loss prediction in this study. The engineering demand parameters (EDPs) for a large number of buildings within a region are efficiently obtained through nonlinear time history analysis (THA) using multi-story concentrated-mass shear (MCS) models. The building data, including structural and nonstructural components, are obtained through field investigation, structural and architectural drawings, and default database published in the FEMA-P58 document. A case study of Tsinghua University campus in Beijing is performed to demonstrate the implementation and advantage using proposed FEMA-P58 method for regional earthquake loss prediction. The results show the advancement in loss simulation for a region, and in identifying the influence of the different ground motion characteristics (e.g., velocity pulse) on the regional loss.

Keywords: earthquake engineering; FEMA-P58; earthquake economic loss; regional seismic damage simulation; next-generation performance-based seismic design

Correspondence information:

Professor Xinzheng LU

Department of Civil Engineering, Tsinghua University, Beijing 100084, China

Telephone: +86-10-62795364

Email: luxz@tsinghua.edu.cn

DOI: 10.1007/s11069-016-2307-z

1.    Introduction

Earthquakes are one of the most destructive natural disasters, especially when they occur in an urban area with dense population and high volume of buildings and other civil infrastructures. The seismic resistance of buildings has been improved significantly over the last 3 decades, due to the continuous advancement in earthquake engineering research. As a consequence, earthquake induced building collapses and casualties on new constructions have been effectively controlled. By contrast, the economic loss due to earthquake is still very high. For example, after the devastating 1960 M9.5 Valdivia earthquake in Chile, a strict building code was implemented in Chile (Guha-Sapir et al. 2011). As a result, during the 2010 M8.8 Maule earthquake in Chile, only 4 buildings constructed after 1985 were collapsed (MAE Center 2010). But this earthquake still caused a direct economic loss of US$ 30.9 billion [Ｋ] which represented 24.2% of the global economic damages from all natural disasters in 2010 (US$ 127.8 billion) (Guha-Sapir et al. 2011). The economic loss could be even higher if the earthquake strikes other highly urbanized regions, as it has occurred in the 2011 M9.0 Tohoku earthquake which caused US$ 210 billion direct loss (Ponserre et al. 2012). Hence, it is crucial to develop a robust earthquake loss prediction model for an urban area, where the information can be used by the decision makers to make informed risk management decisions.

HAZUS (FEMA 1999; FEMA 2012a) is one of the most widely used methods for regional earthquake loss prediction (e.g. Peterson and Small 2012; Remo and Pinter 2012). HAZUS calculates the building response using capacity spectrum method (CSM) (Kircher et al. 2006), in which buildings are treated as a single-degree-of-freedom (SDOF) system when subjected to a pushover load. As a result, there are three major limitations when using HAZUS to predict regional earthquake loss: (1) Because the SDOF model used within HAZUS cannot accurately differentiate the response at different stories and the financial loss may vary significantly at different stories, the economic loss cannot be accurately predicted using the HAZUS method; (2) As stated in the FEMA-445 report, the nonstructural components in the HAZUS method are rather general (FEMA 2006). The financial loss for the nonstructural components cannot be characterized well using the HAZUS method. (3) The influence of the ground motion characteristics (e.g., near-field velocity pulses) on the building damage and economic loss cannot be easily considered using the CSM (Lu et al. 2014).

Since 2002, the Federal Emergency Management Agency (FEMA) funded a 10-year project to define the objective and procedure of next-generation performance-based seismic design which eventually became the FEMA-P58 report: ※Seismic Performance Assessment of Buildings, Methodology and Implementation§ (referred to as ※the FEMA-P58 method§ hereafter) (FEMA 2012b; FEMA 2012c). This report provides a solution for the above limitations of the HAZUS method. The fragility of every structural and nonstructural component in a building is directly considered in the FEMA-P58 method during the seismic assessment. The FEMA-P58 method has been successfully applied to many individual buildings (Yang et al. 2012; Shoraka et al. 2013; Yang and Murphy 2014; Yang et al. 2014; Shome et al. 2015). The Global Earthquake Model (GEM) vulnerability assessment guidelines (Meslem and D＊Ayala 2012; D＊Ayala et al. 2015) further proposed the methods to develop the fragility curves and consequence functions for different regions. However, currently there is no such application for regional predictions. The primary challenge when using the FEMA-P58 method for regional earthquake loss predictions is the difficulty of obtaining detailed seismic responses (i.e., engineering demand parameters, or EDPs) and collecting the structural and nonstructural component data for every building in the region.

To address this limitation, a practicable approach for regional earthquake loss prediction based on the FEMA-P58 method is proposed in this study. This approach allows detailed prediction of the economic loss at each story of each building in a region. To obtain the EDPs of each building, a series of multi-story concentrated-mass shear (MCS) models were developed and used in the nonlinear time history analyses (THA). The building data and the structural and nonstructural component information were obtained through field investigation and design drawings. The values of the fragility curves were adopted from FEMA-P58 study. It should be noted that the default values from the FEMA-P58 for structural and nonstructural components should be modified if they are used in China. However, the purpose of this work is to illustrate the process of applying the FEMA-P58 methodology, not to redefine the fragility data information for all buildings in China (which will be implemented in the future study). In addition, such default values are convenient for readers to understand the results of this study. Hence, the default values as presented in the FEMA-P58 document were used. Two buildings in the Tsinghua University campus located in Beijing, China were chosen as the demonstration buildings for the detailed implementation of the proposed earthquake loss assessment of a region. Finally, an intensity-based earthquake loss prediction model of the entire Tsinghua University (including 619 buildings) was performed. The outcomes of this work can be used as a reference for future earthquake loss prediction model for large urban areas.

2.    Loss prediction methodology

The fundamental principle of the FEMA-P58 loss assessment methodology is the performance-based earthquake engineering framework supported by the Pacific Earthquake Engineering Research Center (Cornell and Krawinkler 2000; Moehle and Deierlein 2004; Yang et al. 2009). Three loss prediction methodologies have been proposed in FEMA-P58 document (FEMA 2012b). The intensity-based method requires an user-specified earthquake intensity; while the scenario-based and the time-based method are based on the intensity-based method, except that these two methods require more earthquake hazards information, such as a specific fault relative to the building site, the ground motion attenuation relationship, and the seismic hazard curve for the site. To obtain such information, extra seismology study is needed, which is not the focus of this work. Therefore, the simplest method, i.e., intensity-based assessment method, was adopted. The procedure relies on the use of conditional probability, where the probability of the exceedance of an EDP demand is conditioned on the probability of the earthquake intensity occurred. Similarly, the probability of incurring a damage at different damage states is conditioned based on the occurrence of a given EDP. Once the damage state is identified, the repair action and repair cost are calculated from a look up table (FEMA 2012b). Because there is lack of available and suitable ground motion and the THA is very time consuming, Yang et al. (2009) developed a practical implementation of the above framework by utilizing a Monte Carlo approach. The proposed Monte Carlo approach is adopted by FEMA-P58 document (FEMA 2012b) and has been implemented into many earthquake loss predictions for individual buildings (Yang et al. 2012; Shoraka et al. 2013; Yang and Murphy 2014; Yang et al. 2014). This research further expanded the above mentioned method to quantify the earthquake loss of an urban region.

2.1  Flowchart of the FEMA-P58 method

Figure 1 shows the flowchart of applying the FEMA-P58 method for an urban area. The process consists of three parts: 1) assemble the building performance model; 2) analyze the building response to determine EDPs; and 3) calculate the economic loss.

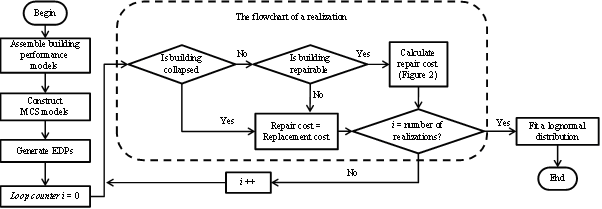
Fig. 1 Flowchart of the FEMA-P58 methodology for building earthquake loss prediction.

During the assembly of the building performance models, basic building data (e.g., the number of buildings, building type, number of stories, floor area and occupancy), fragility and repair cost of vulnerable structural and nonstructural components on each building story shall be collected. The components that are vulnerable to the same EDP can be categorized into one group, referred to as the ※performance group (PG)§. The probability of the component in each damage state is presented using fragility curves, which are developed from a large number of statistical data, experimental data and expert opinions. Given the value of an EDP, the probability of incurring a particular damage state of each PG can be calculated from its fragility curves. Then, the repair cost of a PG is calculated according to the consequence function corresponding to each damage state. Figure 2 shows the procedure to identify the repair costs: (a) The EDP is calculated using THA with the MCS model using the ground motion records selected; (b) The damage state is determined using the fragility curves; (c) The repair cost is then determined according to the total quantity and unit repair cost of each PG. Details are described in Chapter 3 and Chapter 7 of FEMA (2012b).

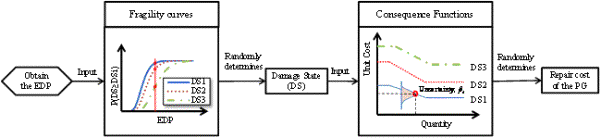
Fig. 2 The calculation of repair cost for a PG

The EDPs including the peak floor acceleration (PFA), peak floor velocity (PFV), peak inter-story drift ratio (IDR), and residual drift at each story are recorded from a series of THA. Using the procedure presented in Yang et al. (2009), a statistical correlated distribution of the EDPs is generated. Using the synthetically generated EDP matrix, the repair cost is then identified from a look up table. It should be noted, as seen in Figure 1, if the building is considered collapsed or irreparable according to its collapse fragility and repair fragility curves (FEMA 2012b), the repair cost is considered as the replacement cost of the building. Otherwise the earthquake loss is calculated by adding up the repair cost of every component under different damage states. The process is executed repeatedly to quantify the distribution of the repair cost of the building.

2.2  Challenges and recommended procedure to extend the FEMA-P58 method to a region

The key challenges of using the FEMA-P58 method to a region are: (1) the assembly of performance models, (2) rapid calculation of EDPs, and (3) prediction of the collapse fragility of a building group. Figure 3 shows the recommended procedure.

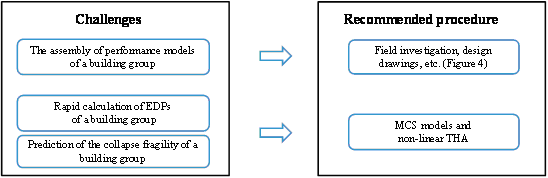
Fig. 3 Challenges and recommended procedure of extending the FEMA-P58 method to a region

(1) Assembly of the performance models

The performance model of buildings contains the basic information with both the structural and nonstructural PGs. The information can be collected through the procedure as shown in Figure 4. The basic building data can be obtained from a geographic information system (GIS) database, field investigation, or design drawings. Generally, such information is easy to collect if a GIS database of the target area is available.

Fig. 4 Approach to assembling the performance models of a building group

If the exact replacement value of the building is missing, the replacement value of the building can be determined by summing the average repair cost of each PG at its most severe damage state. Such procedure might be a simple yet practical approximation. To validate the reliability of the predicted replacement value, the replacement value of the case study region in this work is also estimated using the method proposed in the HAZUS technical manual (FEMA 2013). The replacement values predicted by the HAZUS method and the sum of the median replacement costs of components are US$ 6.905 billion and 7.476 billion, respectively. The HAZUS method predicted a slightly smaller total replacement value, but the difference is not significant and both predictions are acceptable in this case study considering the random nature of the replacement value. In addition, the sum of the median replacement costs of components is more adaptive because it explicitly considers the values of individual components and contents.

Three recommended procedures have been proposed to determine the structural PGs.

(a) Method A: If the structural and architectural drawings of the building are available, the type and quantity of each PG can be obtained from these drawings directly. In some urban region, where similar buildings are constructed at the same period, using the same structural design codes, the information obtained from one building can be duplicated to the other buildings in the region.

 Once the PG information has been identified, the repair cost for the PG can be defined using the fragility data published by the FEMA-P58 document. It should be noted that as a part of the 10-year effort for the FEMA-P58 project, more than 700 fragility curves and associated consequence functions have been identified using a large number of statistical data, experimental data and expert opinions. The structural performance groups are defined based on the material, size and behavior of structural components. Each PG is used to describe one type of structural components. For example, ※B1041.041b§ (one of the PGs used in this study) is applicable to the reinforced concrete moment frames with 24 in. x 24 in. beam size (FEMA 2012c). Details of PG clarification can be found in Appendix A of FEMA (2012c).

(b) Method B: If structural and architectural drawings of the target building are not available, but there is a similar building (with similar year of construction, structural type and occupancy) in the neighborhood, the quantity of the structural PGs of the target building can be estimated by

                                                                 (1)

where A, A₀ and Q, Q₀ are the floor area and quantity of the PG of the target building and the neighborhood building with actual structural and architectural data, respectively.

(c) Method C: For buildings where neither the design information nor similar building information is available, the PG information can be estimated according to the field investigation of the buildings.

To determine the nonstructural PGs information, the buildings are categorized into groups according to building occupancies. For example, the building inventory for a region can be characterized as office buildings (e.g. 30%), residential buildings (e.g. 50%) and industrial buildings (e.g. 20%). In each group of occupancy (e.g. office buildings), the distribution of the nonstructural PGs can be identified from a detailed site visit of several typical buildings. Other PGs which are difficult to estimate (such as pipelines) can be identified according to the normative quantity information provided by Appendix F of FEMA (2012b). For example, the sanitary waste piping in an office building is assumed to be 0.057 feet per 1 gross square foot according to Appendix F of FEMA (2012b), so the length of sanitary waste piping in an office building with a floor area of 1000 m² is 187 m at each floor. For other specialized buildings, the nonstructural PGs can be estimated according to Appendix F of FEMA (2012b).

Note that the above approaches of assembling performance models require some efforts. However, it can be implemented in parallel by groups of people with basic knowledge of architectural and structural engineering. For the case study of Tsinghua University campus (as presented in this work), the data collection of the performance model of all 619 buildings were established by 11 students in 4 weeks. As for the assessment of an entire city, Building Information Model (BIM) can be used to systematically store and identify the building PGs.

(2) Rapid calculation of the EDPs of a building group.

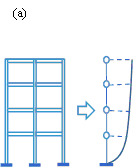
Another difficulty in extending the FEMA-P58 method from an individual building to a region is to obtain the EDP distribution in an efficient manner. For an urban area consisting of thousands of buildings, the establishment of refined computational models is extremely time consuming. It requires a professional understanding of structural engineering, such as the finite element modeling of beams, columns and shear walls, to develop the refined computational model. Even if the refined computational model of a building group can be efficiently established, the resulting computational workload is still extremely expensive (Sobhaninejad et al. 2011). To overcome these difficulties, the multi-story concentrated-mass shear (MCS) models (Figure 5a) proposed by Lu et al. (2014) were adopted in this study. MCS model is a common numerical model to simulate the nonlinear response of multiple-story buildings. MCS model assumes that:

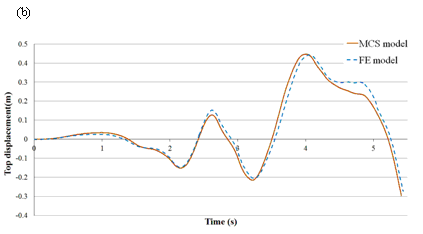
Fig. 5 The multi-story concentrated-mass shear (MCS) models proposed by Lu et al. (2014): (a) illustration; (b) validation (Xu et al. 2014)

(a) A multiple story building can be simplified to a multiple degree-of-freedom (MDOF) model, where each story has its nonlinearity;

(b) The nonlinear response of the building is assumed to be dominated by the shear mode;

(c) Depending on the structural system, the nonlinearity of the structure at each story can be modeled using either modified-clough, bilinear elasto-plastic or pinching model.

MCS models are suitable for regional seismic response analysis (Lu et al. 2014; Xu et al. 2016). Lu et al. (2014) proposed a modeling approach, by which all of the parameters of MCS models can be determined by either refined finite element (FE) models or the basic information of the buildings (i.e., structural type, number of stories, occupancy, construction year, and floor area). The MCS model was compared with a refined FE model by Xu et al. (2014). For a 6-story reinforced concrete (RC) frame, the top displacement versus time histories predicted by the FE model and the MCS model agree well with each other (Figure 5b). Based on the MCS models and non-linear THA, Xu et al. (2014) performed a regional seismic response analysis for the city of Shantou, China. It took less than 10 min to complete the non-linear THA of one ground motion for the region with 7,449 buildings on a desktop computer (Intel 2.8 GHz i5 CPU; 4-GB memory), which demonstrated the efficiency of using the MCS model. Other simplified MDOF models, for example the fishbone model (Nakashima et al. 2002; Luco et al. 2003), can also be used if the model parameters of a large number of buildings can be conveniently determined.

(3) Prediction of the collapse fragility of a building group.

As indicated in the FEMA-P58 methodology, the collapse fragility curves of buildings are needed for the loss calculation. The response analysis of buildings adopted in this work based on the MCS model and non-linear THA can estimate whether a building will collapse when subjected to a particular ground motion (Xu et al. 2014). Thus, the collapse fragility curves can be obtained directly by conducting an incremental dynamic analysis (IDA) using the proposed MCS model for each building.

3.    Case study: regional earthquake loss prediction of the Tsinghua University campus

3.1  Introduction of the case study region

The campus of Tsinghua University, consisting of 619 buildings, has a gross area of approximately 4 km². According to the Chinese Code for Seismic Design of Buildings (CMC 2010), the buildings in Tsinghua University have a seismic design intensity of VIII (with the peak ground acceleration (PGA) of 0.2 g at the 10% probability of exceedance in 50 years hazard level). According to the geological investigation, the site condition of the campus is class II in Chinese code, which approximately corresponds to site class C and D as presented in the ASCE 7-10 document in the United States (Luo and Wang 2012; ASCE 2010).

Figure 6 shows the percentage of different structural types and building occupancies. In terms of structural type, more than half of the buildings are masonry structures. Other major structural types are RC frames, RC shear walls and RC frame-shear wall dual-systems. In terms of occupancy, residential buildings comprise more than 50%, and other major occupancies are offices, research facilities and classrooms.

Fig. 6 Percentages of (a) different structural types and (b) building occupancies

3.2  Assembly of the building performance model

Eleven students were assigned to collect the structural drawings and perform the field investigations. Table 1 shows the building inventory collected using the 3 methods outlined in Figure 4.

Table 1. Results of the building investigation according to the completeness of the structural data

A RC frame office building (named RC_Office) and a masonry residential building (named Mas_Residence) were selected as the two demonstration examples for the seismic performance assessment using the proposed FEMA-P58 approach. Table 2 shows the basic facts about the two example buildings selected.

Table 2. Basic data for the two example buildings

3.3  Ground motion selection and scaling

The following steps are proposed in FEMA-P58 for ground motion selection and scaling: (1) Select a target spectrum that is suitable for the site (typically use site specific hazard analysis); (2) Select ground motions with spectral shapes that are similar to the target spectrum over a period range of interest; (3) Amplitude-scale the selected ground motions such that the spectra will match the target spectrum. In this work, some simplifications were adopted for the ground motion selection and scaling:

(1) Because the latest strong earthquake happened in Beijing is M8.0 Sanhe-Pinggu earthquake in 1679, more than 200 years before strong motion seismograph was developed, there are few strong motion records in Beijing. As a result, 50 pairs of the horizontal components of the ground motion records for site classes C and D proposed by FEMA P695 (FEMA 2009) are adopted in this work. This includes the 22 pairs of ground motions from the far-field records, 14 pairs of ground motions from the near-field records (with pulse), and 14 pairs of ground motions from the near-field records (without pulse). These ground motions are adopted because (a) their site conditions are similar to those of the case study region (i.e., site classes C and D); (b) these ground motions have been widely used in related studies (Lu et al. 2013; Lu et al. 2014; Shi et al. 2014), so these results can be easily compared to other studies; and (c) the main purpose of this work is to demonstrate the feasibility of using the FEMA-P58 method to assess the seismic performance of a region, rather than an actual engineering application, so these ground motions are selected.

(2) FEMA-P58 suggests using S_a(T₁) as the intensity measure. However, in this work, hundreds of buildings are analyzed simultaneously in the THA. T₁ varies between buildings, it will be inappropriate to analyze the entire region using one S_a(T₁) value. Using various S_a(T₁) may result in significantly different ground motion scaling factors among neighborhood buildings, which is also unreasonable. Moreover, PGA is the seismic intensity measure adopted in the Chinese Code for Seismic Design of Buildings (CMC 2010) for the design of all kinds of structures. Hence, PGA is selected to quantify the shaking intensity.

(3) Because the case study (Tsinghua University) is not overly a large area where the site condition is significantly different, the same set of ground motion is used for each building. For other study, where the area is large or the site condition is complex, more detailed sets of ground motions should be used for each building.

Three earthquake shaking intensities namely the service level earthquake (SLE), design basis earthquake (DBE), and maximum considered earthquake (MCE) were included in this study. The corresponding PGAs and return periods are shown in Table 3 according to Section 5.1.2 and Table 5.1.2-2 in CMC (2010).

Table 3. Return periods and the corresponding PGAs

4.    Results and discussion on loss prediction

4.1  Validations

Due to the lack of credible and accurate studies of regional seismic loss in the target area, the loss results in this study are not able to be compared with other studies. Instead, the earthquake loss results of typical buildings are compared with those calculated using PACT (an earthquake loss simulation software developed by FEMA to implement FEMA-P58 method (FEMA 2012b)) for validation.

Taking RC_Office as an example, the loss was normalized based on the building replacement value. Figure 7 shows the comparison of the earthquake loss from current study and the results obtained from the PACT software. Each curve in Figure 7 consists of 1000 points generated by 1000 times of the Monte Carlo approach. For clarity, only a few points on the curves are marked. The points on the vertical line at the right end of the curves stand for the realizations where the building is predicted to collapse or damage irreparably, viz., the loss ratio is 100%. As shown in this figure, the loss simulation results are very similar.

Fig. 7 Comparison of the loss results of RC_Office predicted by the proposed method and by PACT software at the hazard levels of SLE, DBE, and MCE.

4.2  Earthquake loss predictions of the two example buildings

Figure 8 shows the results of the loss simulation of the two example buildings. At the SLE hazard level, the RC_Office building has minor losses. There is nearly no loss contributed from the structural (Str) PGs as all components remain elastic. By contrast, there are some damages related to the drift-sensitive nonstructural (NSD) PGs. This is mainly due to the repair cost of the partitions and the wall finishes. When the shaking intensity reaches the DBE hazard level, the loss associates with the structural and acceleration-sensitive nonstructural (NSA) PGs increases. By contrast, the loss for the Mas_Residence is higher than the RC_Office building, this shows the masonry structures are more sensitive to deformation. The proposed approach also allows the users to identify the distribution of the structural response among different stories. For example, Figure 9 shows the distribution of peak IDR and PFA of RC_Office at the MCE hazard level.

Fig. 8 Loss result of (a) RC_Office and (b) Mas_Residence under the three hazard levels considered

Fig. 9 The distribution of (a) peak IDR and (b) PFA of RC_Office at the MCE hazard level.

Figure 10 shows the detailed loss of nonstructural PGs at each story of the RC_Office building. The result shows that a high percentage of the repair costs come from the nonstructural walls (including exterior walls, partitions, and wall finishes). The walls start to crack and contribute to the repair costs even when the peak IDR is small. The repair costs of the teleconference equipment on the 3rd story and the computers on the 4th story are noticeable because the teleconference equipment is expensive and the quantity of computers on the 4th story is considerably larger than on other stories. Therefore, the loss prediction clearly represents the property distribution characteristics within the RC_Office building.

Fig. 10 The loss details of nonstructural PGs at each story of RC_Office under the hazard levels of (a) SLE, (b) DBE and (c) MCE

4.3  Earthquake loss prediction of the entire campus

Figure 11a shows the earthquake loss prediction of the entire campus under three levels of earthquake shaking intensities. The total earthquake loss ratio is defined as the ratio of total earthquake loss to the total replacement value (US$ 7.476 billion) of the region. The median total loss ratio are 1.3%, 13.7% and 34.9% for the SLE, DBE and MCE hazard level, respectively. The median loss is further classified into the losses due to building collapse, irreparable deformation, and repair cost. Figure 11b shows the distribution of the median repair cost. At the SLE hazard level, the economy loss is mainly concentrated from repair costs. When the earthquake intensity increases, the loss starts to contribute from both repair costs and irreparable deformation. As the shaking intensity reaches the MCE hazard level, the contribution from the collapse-induced loss is introduced but the percentage is very low (less than 2%), which is similar to the loss results observed in the 2010 Chile earthquake (MAE Center 2010) and 2011 Christchurch earthquake (Smyrou et al. 2011).

Fig. 11 Loss results of the entire campus under the three hazard levels considered: (a) Cumulative probability of the total earthquake loss ratio; (b) distribution of the total earthquake loss ratio

In addition to the loss assessment from the 50 pairs of ground motions, a side study about the influence of the ground motion velocity pulse on the building performance and earthquake loss is also studied in this work. The results from the loss simulation were compared between the 14 pairs of near-field records with pulse and the 14 pairs of near-field records without pulse. As shown in Figure 12, the economic loss increases when the region is subjected to pulse type motion. Therefore, the proposed approach is able to account for the influence of ground motion characteristics, such as velocity pulse, on building earthquake response and loss prediction. By contrast, in the HAZUS method, building response is determined by the intersection of the building capacity curve and the earthquake response spectrum (Kircher et al. 2006; Xiong et al. 2016), known as the Capacity Spectrum Method (CSM) (ATC 1996). According to the discussion by Krawinkler and Seneviratna (1998), due to the fact that CSM is based on static loading, it cannot represent dynamic phenomena with high accuracy. As a result, the proposed approach improves one of the limitations from the HAZUS simulation approach.

Fig. 12 The influence of velocity pulse on the economic loss of the case study region detected by the proposed method.

5.    Conclusions

With the increasing improvement of the building codes, earthquake-induced building collapses and casualties have been well controlled. However, hefty financial losses due to earthquake are still impacting many major cities in high seismic zones. To effective quantify the earthquake loss of a major city center, the FEMA-P58 method was used. To efficiently analyze the seismic performance of a region, simplified MCS models were developed and used with non-linear THA to quantify the seismic response. The intensity-based earthquake loss prediction was implemented in Tsinghua University to demonstrate the implementation and advantage of the proposed approach. The following conclusions are obtained:

(1) MCS models can be used to calculate the EDPs for each building at each story with high efficiency, which solves one of the key challenges of the extension of FEMA-P58 method from an individual building to a region.

(2) For the case study, when the shaking intensity reaches the SLE hazard level, the total earthquake loss mainly contributes from the repair costs. On the other hand, when the hazard level increases to the MCE, the total earthquake loss mainly contributes from the repair cost and the cost of the demolition and reconstruction of irreparable buildings. The percentage of loss caused by building collapse is low.

(3) The proposed approach can be used to study the influence of ground motion characteristics, such as velocity pulse, on building earthquake response and loss, which improves one of the limitations of the HAZUS method.

Note that the purpose of this work is to propose a practical approach for regional earthquake loss prediction to take advantage of the benefits of next-generation performance-based seismic design instead of conducting a precise prediction for Tsinghua University campus. The accuracy of the loss result relies on the quality of the data. The fragility curves, consequence functions and normative quantities used in this work are the proposed default values in FEMA-P58. Due to the differences between China and the United States, such default data may not be sufficiently accurate if they are used for Chinese buildings. In the future, these data will be further carefully determined to represent the characteristics of the region to be analyzed. Thus, the proposed loss prediction approach will have a higher accuracy and a more significant contribution to disaster prevention in cities.

Acknowledgements

The authors are grateful for the help from Runhua Gong, Qiuhan Huang, Huiping Li, Jian Liu, Shixuan Liu, Yizhe Meng, Yao Ming, Jian Yang, and Zhebiao Yang in the investigation and collection of basic building data, building design drawings, and property distribution, which forms the data basis of this work. The authors are also grateful for the financial support received from the National Natural Science Foundation of China (No. 51578320, 51378299), the National Key Technology R&D Program (No. 2015BAK14B02), and the National Non-profit Institute Research Grant of IGP-CEA (Grant No: DQJB14C01).

References

American Society of Civil Engineers (ASCE) (2010) Minimum Design Loads for Buildings and Other Structures, ASCE/SEI 7-10, Reston, VA

ATC (1996) Seismic evaluation and retrofit of concrete buildings (ATC-40). Applied Technology Council, Redwood City, California

China Ministry of Construction (CMC) (2010) Code for Seismic Design of Buildings, GB50011-2010, China Architecture and Building Press, Beijing, China (in Chinese)

Coin News (2015) US Inflation Calculator. http://www.usinflationcalculator.com/

Cornell CA, Krawinkler H (2000) Progress and Challenges in Seismic Performance Assessment. PEER Center News 3(2):1-3.

D＊Ayala D, Meslem A, Vamvatsikos D, Porter K, Rossetto T, Crowley H, Silva V (2015) Guidelines for Analytical Vulnerability Assessment of Low/Mid-Rise Buildings, GEM Technical Report 2015-08 V1.0.0.

Federal Emergency Management Agency (FEMA) (1999) Earthquake Loss Estimation Methodology - Hazus99, Technical Manual, Washington, DC

Federal Emergency Management Agency (FEMA) (2006) Next-Generation Performance-Based Seismic Design Guidelines Program Plan for New and Existing Buildings. Tech. Rep. FEMA-445, Washington DC

Federal Emergency Management Agency (FEMA) (2009) Quantification of Building Seismic Performance Factors. Tech. Rep. FEMA-P695, Washington DC

Federal Emergency Management Agency (FEMA) (2012a) Multi-Hazard Loss Estimation Methodology Hazus 每MH 2.1 Advanced Engineering Building Module (AEBM) Technical and User＊s Manual. Washington, DC

Federal Emergency Management Agency (FEMA) (2012b) Seismic Performance Assessment of Buildings Volume 1 每 Methodology, Tech. Rep. FEMA-P58, Washington, DC

Federal Emergency Management Agency (FEMA) (2012c) Seismic Performance Assessment of Buildings Volume 2 - Implementation Guide, Tech. Rep. FEMA-P58, Washington, DC

Federal Emergency Management Agency (FEMA) (2013) Multi-hazard Loss Estimation Methodology 每 Earthquake Model, Hazus-MH 2.1, Technical Manual, Washington, DC

Guha-Sapir D, Vos F, Below R, Ponserre S (2011) Annual Disaster Statistical Review 2010: The Numbers and Trends. Centre for Research on the Epidemiology of Disasters (CRED). Brussels, Belgium

Kircher CA, Whitman RV, Holmes WT (2006) Hazus Earthquake Loss Estimation Methods. Nat Hazards Rev  7(2):45-59

Krawinkler H, Seneviratna GDPK (1998) Pros and cons of a pushover analysis of seismic performance evaluation. Eng Struct 20(4): 452-464

Lu XZ, Han B, Hori M, Xiong C, Xu Z (2014) A Coarse-Grained Parallel Approach for Seismic Damage Simulations of Urban Areas Based on Refined Models and GPU/CPU Cooperative Computing. Adv Eng Softw  70:90-103

Lu X, Ye LP, Lu XZ, Li MK, Ma XW (2013) An Improved Ground Motion Intensity Measure for Super High-rise Buildings.      Sci China Technol Sci 56(6):1525-1533

Luco N, Mori Y, Funahashi Y, Cornell CA, Nakashima M (2003) Evaluation of predictors of non-linear seismic demands using ＆fishbone＊ models of SMRF buildings. Earthq Eng Struct D 32(14):2267-2288

Luo KH, Wang YY (2012) Researches About the Conversion Relationships Among the Parameters of Ground Motions in the Seismic Design Codes of China, America and Europe. In: Proceedings of the 15^th World Conference on Earthquake Engineering, Lisbon, Portugal

Meslem A, D＊Ayala D (2012) Toward worldwide guidelines for the development of analytical vulnerability functions and fragility curves at regional level. In: Proceedings of the 15^th World Conference on Earthquake Engineering, Lisbon, Portugal

Mid-America Earthquake Center (MAE Center) (2010) The Maule (Chile) Earthquake of February 27, 2010: Consequence Assessment and Case Studies. Report No.10-04, Urbana, IL

Nakashima M, Ogawa K, Inoue K (2012) Generic frame model for simulation of earthquake responses of steel moment frames. Earthq Eng Struct D 31(3):671每692

Moehle J, Deierlein GG (2004) A Framework Methodology for Performance-Based Earthquake Engineering, Paper No. 679. In: Proceedings of the 13^th World Conference on Earthquake Engineering, Vancouver, BC, Canada

Peterson J, Small MJ (2012) Methodology for Benefit每Cost Analysis of Seismic Codes. Nat Hazards 63:1039-1053

Ponserre S, Guha-Sapir D, Vos F, Below R (2012) Annual Disaster Statistical Review 2011: The Numbers and Trends. Centre for Research on the Epidemiology of Disasters (CRED). Brussels, Belgium

Remo JW, Pinter N (2012) Hazus-MH Earthquake Modeling in the Central USA. Nat Hazards 63:1055-1081

Shi W, Lu XZ, Guan H, Ye LP (2014) Development of Seismic Collapse Capacity Spectra and Parametric Study. Adv Struct Eng 17(9):1241-1256

Shome N, Jayaram N, Krawinkler H, Rahnama M (2015) Loss Estimation of Tall Buildings Designed for the Peer Tall Building Initiative Project. Earthq Spectra 31(3):1309-1336

Shoraka MB, Yang TY, Elwood KJ (2013) Seismic Loss Estimation of Non坼Ductile Reinforced Concrete Buildings. Earthq Eng Struct D 42(2):297-310

Smyrou E, Tasiopoulou P, Bal HE, Gazetas G (2011) Ground Motions Versus Geotechnical and Structural Damage in the February 2011 Christchurch Earthquake. Seismol Res Lett 82(6):882-892

Sobhaninejad G, Hori M, Kabeyasawa T (2011) Enhancing Integrated Earthquake Simulation with High Performance Computing. Adv Eng Softw 42(5SI):286-292

Xiong C, Lu XZ, Guan H, Xu Z (2016) A Nonlinear Computational Model for Regional Seismic Simulation of Tall Buildings. B Earthq Eng 14(4): 1047-1069

Xu Z, Lu XZ, Guan H, Han B, Ren AZ (2014) Seismic Damage Simulation in Urban Areas Based on a High-Fidelity Structural Model and a Physics Engine. Nat Hazards 71(3):1679-1693

Xu Z, Lu XZ, Guan H, Tian Y, Ren AZ (2016) Simulation of earthquake-induced hazards of falling exterior non-structural components and its application to emergency shelter design. Nat Hazards 80(2): 935-950

Yang TY, Murphy M (2014) Detailed Performance Evaluation of Steel Seismic Force Resisting Systems for Low-Rise Buildings in Canada. Earthquake Spectra In-press

Yang TY, Atkinson JC, Tobber L (2014) Detailed Seismic Performance Assessment of High-Value Contents Laboratory Facility. Earthq Spectra. doi: 10.1193/092313EQS259M

Yang TY, Moehle JP, Stojadinovic B, Der Kiureghian A (2009) Seismic Performance Evaluation of Facilities: Methodology and Implementation. J Struct Eng-ASCE 135(10):1146-1154

Yang TY, Moehle JP, Bozorgnia Y, Zareian F, Wallace JW (2012) Performance Assessment of Tall Concrete Core坼Wall Building Designed Using Two Alternative Approaches. Earthq Eng Struct D 41(11):1515-1531