|
4 Validation and application of the proposed
model to individual building structures
To
validate the proposed model and the associated parameter calibration method,
the NMFS models of two tall buildings are established and the predicted seismic
responses are compared with those of the refined FE models, as presented in
Figure 7. Building A is a 15-story RC frame-shear wall structure (see Figure
7(a)), details of which can be found in Ren et al. (2015).
Building B is a 42-story RC frame core-tube building (i.e., Building 2N in Lu
et al. (2015)), as shown in Figure 7(b). These
two buildings are selected because such types of structures are widely used
and representative. The RC frame-shear wall structure is commonly used for apartments
and hotels, whereas the RC
frame core-tube structure is popularly used for offices and commercial centers.
The attribute data of the two buildings are listed in Table 1.
The refined FE models of the two buildings (Figure 7)
are established using the general purpose FE software MSC.MARC, in which shear
walls and frames are modeled with multi-layer shell elements and fiber beam
elements (Lu et al. 2013a). The total numbers
of elements are 25,238 and 36,547, respectively, for Buildings A and B. The
modeling details and the accuracy of the refined FE model have already been
discussed in the work of Ren et al. (2015) and
Lu et al. (2015).
|
|
|
|
(a) Building
A (15-story RC frame-shear wall structure)
|
(b) Building B (42-story RC frame core-tube
structure)
|
Figure
7. Illustration
of the refined FE models
Table 1. Building
attribute data
|
Name
|
Number
of stories
|
Height
|
Site
condition
|
Year
of construction
|
Structural
type
|
|
Building
A
|
15
|
54.9m
|
Class
II
|
2013
|
RC
frame-shear wall
|
|
Building
B
|
42
|
141.8m
|
Class
II
|
2013
|
RC
frame core-tube
|
4.1 Demonstration of the calibration process
The
parameters of the NMFS model of Building A in the y-direction (i.e.,
the direction of the first vibration mode) are used to demonstrate the calibration
process. Note that the first and second periods in the y-direction of
Building A have already been obtained through modal analysis of the refined
FE model during the design stage. The flexural and shear stiffnesses are calculated
following the procedures outlined in Section 3.1. Subsequently, modal analysis
of the NMFS model is performed, and the resulting vibration periods are compared
with those of the refined FE model as shown in Table 2. A good agreement is
obtained, as also confirmed by Miranda and Taghavi (2005).
Table 2.
Comparison of the vibration periods
| |
T1
(s)
|
T2
(s)
|
|
Refined
FE model
|
1.4422
|
0.3449
|
|
NMFS
model
|
1.4421
|
0.3473
|
|
Error
|
0.0%
|
-0.7%
|
The design response spectrum for MRSA is determined according
to the Chinese seismic design code (GB50011-2010) (MOHURD 2010b). Subsequently, the SRSS method is adopted
to combine the spectrum responses of different modes. The shear forces in the
shear springs and the bending moments in the flexural springs obtained from
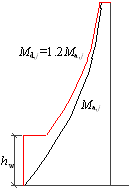
SRSS are demonstrated as the lines with gray triangles in Figure 8. As discussed
in Section 3.2, the shear force and bending moment should be further adjusted
according to the design specifications. Additionally, the modified shear forces
and bending moments, following the requirements set in Equations 15, 16 and
Figure 6, are shown as lines with red diamonds in Figure 8, which represent
the design values of Vd, j and Md, j.
The yield strengths Vy, j and
My, j and the yield displacements Duy,
j and Dqy,
j are calculated
using Equations 17-20, where Wy
= 1.10 for RC frame-shear wall structures (C2H), according to Table 5.5 of the
HAZUS Technical Report (FEMA 2012a). The peak
strengths Vp, j and Mp, j
are calculated according to Equations 21 and 22, with Wu
= 2.50 (FEMA 2012a).
As stated in Section 3.3, two methods can be used to
determine the peak displacements Duu,
j and Dqu,
j. If the stiffness
reduction method is adopted, the stiffness reduction factor h
= 0.7 according to Provision 10.10.4.1 of ACI 318-08 (ACI Committee 2008). If the ductility
factor method is adopted, the ductility factor m
= 4 according to Table 5.6 of the HAZUS Technical Report (FEMA
2012a). Subsequently, the peak displacements Duu,
j and Dqu,
j are calculated
according to Equations 25-31. The hysteretic parameter t
= 0.6 for RC frame-shear wall structures (C2H) according to Table 5.18 of the
HAZUS Technical Report (FEMA 2012a).
|
|
|
|
(a) Shear
forces in the shear springs
|
(b) Bending
moments in the flexural springs
|
Figure 8. Design forces on each
story
As
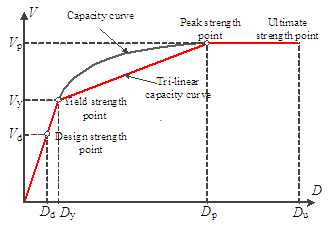
previously discussed, two backbone curves are available to describe the inter-story
hysteretic behavior: (1) bi-linear or (2) tri-linear. In addition, the peak
displacements can be determined using either the stiffness reduction method
or the ductility factor method. Different combinations of these models/methods
are compared to the refined FE model to determine the most accurate prediction
method. To demonstrate the advantages of the proposed NMFS model, the elastic
continuum model of Miranda and Taghavi (2005)
and the NMS model adopted in IES (Hori 2006)
are also included in the comparison. A brief summary of different prediction
models used for the comparison is provided in Table 3.
Table
3. Comparison of different prediction models
|
Model name
|
Model type
|
Backbone
curve
|
Peak displacement
|
Parameters
|
|
Refined
FE model
|
Multi-layer
shell element and fiber beam element
|
--
|
--
|
--
|
|
NMFS-Tri-h
|
Nonlinear
MDOF flexural-shear model
|
Tri-linear
backbone
|
Stiffness
reduction method
|
Wy=1.10
Wp=2.50
h=0.7
|
|
NMFS-Tri-m
|
Nonlinear
MDOF flexural-shear model
|
Tri-linear
backbone
|
Ductility
factor method
|
Wy=1.10
Wp=2.50
m=4
|
|
NMFS-Bi
|
Nonlinear
MDOF flexural-shear model
|
Bi-linear
backbone
|
--
|
Wy=1.10
Wp=2.50
|
|
NMS-Tri-h1
|
Nonlinear
MDOF shear model
|
Tri-linear
backbone
|
Stiffness
reduction method
|
Wy=1.10
Wp=2.50
h=0.7
|
|
Elastic
model2
|
Elastic
continuum model
|
--
|
--
|
--
|
1. The NMS model is calibrated according
to Lu et al.¡¯s work (2014b), where the design
inter-story seismic force is identical to that of the NMFS model.
2. The elastic continuum model
of Miranda and Taghavi (2005) is calibrated
using the same T1, T2 as the NMFS models.
The widely used ground motion recorded at El-Centro station
in the United States in 1940 (PEER 2012) is
selected to perform the comparison. To verify the nonlinear capability of the
proposed NMFS model, the peak ground acceleration (PGA) is adjusted to 220 gal,
which is the intensity of MCE according to the Chinese seismic design code (GB50011-2010)
(MOHURD 2010b) for Building A.
4.2.1 Comparison amongst different NMFS models
The
base shear-roof displacement curves obtained from the pushover analysis under
an inverse triangular load pattern are compared in Figure 9 for Models NMFS-Tri-h, NMFS-Tri-m,
NMFS-Bi, and the refined FE model. It is evident that the global base shear-roof
displacements of the NMFS models exhibit several turning points, because the
shear springs and the flexural springs do not yield simultaneously. Generally,
the tri-linear models are in better agreement with the refined FE model than
the bi-linear model.
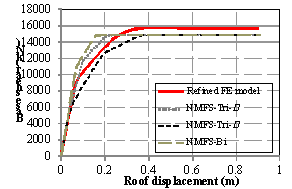
Figure 9. Base shear-roof displacement pushover
curves of Models NMFS-Tri-h,
NMFS-Tri-m, NMFS-Bi and the refined FE model
Subsequently, the nonlinear THA of the four models is
performed. Noting that the inter-story drift ratio is one of the most important
EDPs for loss estimation, the envelopes of the inter-story drift ratios predicted
by the four models are shown in Figure 10. All of the three NMFS models are
in good agreement with the refined FE model. This is a most significant outcome
because an accurate seismic damage prediction relies heavily on the accuracy
of the inter-story drift results. Similar to the finding achieved from Figure
9, the tri-linear models are slightly closer to the refined FE model than the
bi-linear model.

Figure 10. Inter-story drift ratios of Models
NMFS-Tri-h, NMFS-Tri-m,
NMFS-Bi and the refined FE model
4.2.2 Comparison between NMS,
Elastic and NMFS models
Although the NMS model can accurately represent
the inter-story shear deformation mode of frame structures, it cannot characterize
the lateral deformation mode of tall buildings with shear walls. The inter-story
drift ratio envelopes of Model NMS-Tri-h, Model
NMFS-Tri-h and the refined FE model are compared in Figure 11, which
clearly indicates that Model NMS-Tri-h significantly overestimates the inter-story
drift ratio of the lower stories and underestimates the inter-story drift ratio
of the higher stories. As a result, the NMS model cannot be used for seismic
loss estimation of tall buildings because the inter-story drift ratio is a highly
important EDP for such an estimation.
The inter-story
drift ratio envelopes of Model NMFS-Tri-h, Elastic model and the refined FE model are
also compared in Figure 11. As evident in the figure, the result of Elastic model is much smaller than those
of the refined FE model and the NMFS models. The two comparisons above show
that the prediction of Model
NMFS-Tri-h is significantly better.

Figure 11. Inter-story drift ratios of Model NMFS-Tri-h, Model
NMS-Tri-h, Elastic model and the refined FE model
4.2.3 Comparative studies
with multiple ground motions
Considering the random nature of earthquakes,
multiple ground motions are adopted in this section to further demonstrate the
accuracy of the proposed NMFS model. A total of 22 far field ground motions
recommended by FEMA-P695 (FEMA 2009), which
are widely used in many related studies, are input into the refined FE models
and the NMFS models of the two tall buildings. The PGAs are set to 220 gal and
510 gal for Buildings A and B, respectively, corresponding to their MCE levels
specified in the Chinese seismic design code (GB50011-2010) (MOHURD 2010b).
The predicted
maximum inter-story drift ratios of Building A subjected to different ground
motions are compared in Figure 12 using the three NMFS models (i.e., Model NMFS-Tri-h, Model NMFS-Tri-m and Model NMFS-Bi) and the refined FE model.
As evident in Figure 12, though the maximum inter-story drift ratios vary significantly
under different ground motions due to their randomness (Lu et al. 2013c; Lu et al. 2013d), the predicted maximum
inter-story drift ratios of all three NMFS models generally agree well with
those of the refined FE model, which confirms the robustness of the proposed
model. In addition, the seismic
responses show significant nonlinearity. The average ratio of the maximum inter-story
displacement to the yield inter-story displacement under the 22 ground motions
is 5.9. Results also indicate
that Model NMFS-Tri-h has the smallest average error, which is
followed by Model NMFS-Tri-m. The average error of Model NMFS-Bi is the
largest. Such conclusion is similar to the findings obtained from Figures 9
and 10. In view of this, Model NMFS-Tri-h and Model NMFS-Tri-m are
recommended for the regional seismic simulation.
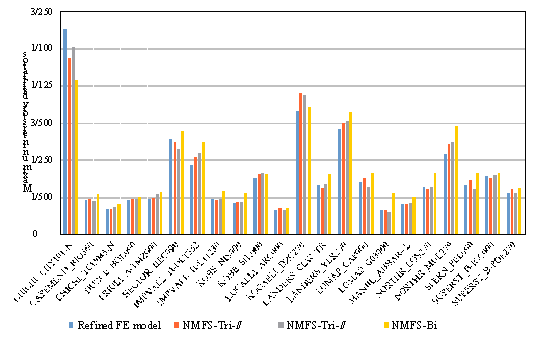
Figure 12. Predicted maximum inter-story drift ratios of Building A subject
to the 22 ground motions
The average
inter-story drift ratios along the height of the two buildings subject to the
22 ground motions are presented in Figure 13. The results of both Model NMFS-Tri-m and Model NMFS-Tri-h are in good agreement with those of the refined
FE model. Given that rather limited information is required to calibrate the
parameters in the proposed NMFS model, the accuracies of the NMFS model and
the associated parameter calibration method are considered acceptable. Note,
for Building A, that the computational time using the NMFS model subjected to
the 22 ground motions is only 135 CPU seconds on a desktop computer (CPU: 2.67-GHz
Intel Xeon X5650, RAM: 48GB of 1333-MHz DDR3), whilst the refined FE model takes
1137 CPU hours. The speedup ratio of 30,320 (= 1137 ¡Á 3600 ¡Â 135) confirms a
remarkable efficiency of the proposed NMFS model.
|
|
|
|
(a)
Building A
|
(b)
Building B
|
Figure 13. Average inter-story drift ratios for Buildings A
and B subject to the 22 ground motions
5 Application of the proposed method to regional buildings
A residential area in China covering nine
tall RC frame-shear wall buildings and two medium-rise RC frame buildings is
investigated to demonstrate the applicability of the proposed model for regional
areas. The GIS data are presented in Table 4 and Figure 14. The nine tall buildings
are analyzed using the NMFS model proposed in this work, and the two medium-rise
buildings are simulated with the NMS model according to the work of Lu et al.
(2014b).
A nonlinear
time-history analysis of this region is implemented subject to El-Centro EW
ground motion in the x-direction with PGA = 400 gal (i.e., the MCE level
ground motion of this region). The seismic displacement responses at the time
step t = 10 s are shown in Figure 15(a). The entire time-history analysis
consumes 261 CPU seconds on a desktop computer (CPU: 2.67-GHz Intel Xeon X5650,
RAM: 48GB of 1333-MHz DDR3) which demonstrates a high computational efficiency.
As demonstrated in Figure 15(b), the envelope of inter-story drift ratios of
each building can be calculated and displayed, which is critical for seismic
loss estimations.
Table 4. Building inventory
|
Label
|
Name of building
|
Number of stories
|
Height
(m)
|
Site condition
|
Year of construction
|
Structural type
|
|
1
|
Yingu
|
23
|
92
|
Class II
|
2000
|
RC frame-shear wall
|
|
2
|
Caizhi
|
28
|
112
|
Class II
|
1998
|
RC frame-shear wall
|
|
3
|
Longhu-1
|
27
|
108
|
Class II
|
2010
|
RC frame-shear wall
|
|
4
|
Longhu-2
|
9
|
36
|
Class II
|
2010
|
RC frame-shear wall
|
|
5
|
Longhu-3
|
25
|
100
|
Class II
|
2010
|
RC frame-shear wall
|
|
6
|
Longhu-4
|
19
|
76
|
Class II
|
2010
|
RC frame-shear wall
|
|
7
|
Longhu-5
|
7
|
28
|
Class II
|
2010
|
RC frame
|
|
8
|
Longhu-6
|
7
|
28
|
Class II
|
2010
|
RC frame
|
|
9
|
Longhu-7
|
18
|
72
|
Class II
|
2010
|
RC frame-shear wall
|
|
10
|
Longhu-8
|
19
|
76
|
Class II
|
2010
|
RC frame-shear wall
|
|
11
|
Longhu-9
|
15
|
60
|
Class II
|
2010
|
RC frame-shear wall
|
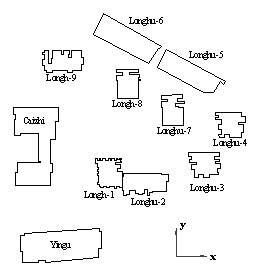
Figure 14. 2D-GIS plan of buildings in a regional area

(a)
Displacements

(b) Envelopes of inter-story drift ratios
Figure 15.
Seismic response results of buildings in a regional area
6 Conclusions
A nonlinear MDOF flexural-shear (NMFS) model
and the associated parameter calibration method are proposed for the regional
seismic damage analyses of tall buildings. The NMFS model has several advantages, including (1) the representation of
the flexural-shear deformation mode of tall buildings, (2) a high computational
efficiency, (3) convenient and efficient parameter calibration and (4) the ability
to output the inter-story drift on each story. By comparing with the widely
used NMS model, the proposed NMFS model is capable of simulating the flexural-shear
deformation characteristics of tall buildings more realistically, and the accuracy
of the predicted inter-story drift is significantly improved. Meanwhile the
computational efficiency is also remarkably enhanced compared with that of the
corresponding refined FE model. In addition, the parameter calibration method
is easy to implement, which only requires widely accessible building attribute
data.
Different calibration
approaches are compared, indicating that the tri-linear backbone curve performs
better than the bi-linear backbone curve. Both the stiffness reduction method
and the ductility factor method demonstrate acceptable accuracies. Finally,
the seismic damage to an urban area of tall buildings is simulated using the
proposed model. The computational efficiency is reasonably high for a large-scale
regional seismic analysis. Overall, this study may facilitate future high-fidelity
regional seismic loss estimations of tall buildings.
Acknowledgements
The authors are grateful
for the financial support received from the National Key Technology R&D
Program (Nos. 2015BAK17B03), the National Natural Science Foundation of China
(No. 51578320), the National Non-profit Institute Research Grant of IGP-CEA
(Grant No: DQJB14C01) and the European Community's Seventh Framework Programme,
Marie Curie International Research Staff Exchange Scheme (IRSES) under grant
agreement n¡ã 612607.
References
ACI Committee (2008)
Building code requirements for structural concrete (ACI 318-08) and Commentary
(318R-08). American Concrete Institute, Farmington Hills, Michigan
Areemit
N, Montgomery M, Christopoulos C, Hasan A (2012) Identification of the dynamic
properties of a reinforced concrete coupled shear wall residential high-rise
building. Can J Civ Eng 39(6):631-642
ASCE
(2010) Minimum design loads for buildings and other structures (ASCE/SEI 7-10).
American Society of Civil Engineers, Reston, Virginia
Campbell
S, Kwok KCS, Hitchcock PA (2005) Dynamic characteristics and wind-induced response
of two high-rise residential buildings during typhoons. J Wind Eng Ind Aerodyn
93(6):461-482
CEN
(2004) Eurocode 8: Design of structures for earthquake resistance. Part 1: General
rules, seismic action and rules for buildings. Comite Europeen de Normalisation,
Brussels
Fajfar
P, Gaspersic P (1996) The N2 method for the seismic damage analysis for RC buildings.
Earthq Eng Struct Dyn 25(1):23-67
FEMA
(1997) NEHRP guidelines for the seismic rehabilitation of buildings (FEMA-273).
Federal Emergency Management Agency, Washington, DC
FEMA
(2009) Quantification of building seismic performance factors (FEMA P695). Federal
Emergency Management Agency, Washington, DC
FEMA
(2012a) Multi-Hazard loss estimation methodology-earthquake model technical
manual (HAZUS-MH 2.1). Federal Emergency Management Agency, Washington, DC
FEMA
(2012b) The seismic performance assessment of buildings, volume 1 methodology
(FEMA P-58-1). Prepared by the Applied Technology Council for the Federal Emergency
Management Agency, Washington, DC
Gao
YQ, Liu WF (2012) Statistical analysis of fundamental periods of frame-shear
wall structures. Appl Mech Mater 174-177:2071-2078
Gilles
D, McClure G (2012) Measured natural periods of concrete shear wall buildings:
insights for the design of Canadian buildings. Can J Civ Eng 39(8):867-877
Gu¨¦guen
P, Michel C, LeCorre L (2007) A simplified approach for vulnerability assessment
in moderate-to-low seismic hazard regions: application to Grenoble (France).
Bull Earthquake Eng 5(3):467-490
Gupta
A, Krawinkler H (2000) Dynamic P-delta effects for flexible inelastic steel
structures. J Struct Eng 126(1):145-154
Hori
M (2006) Introduction to computational earthquake engineering. Imperial College
Press, London
Ibarra
LF, Krawinkler H (2005). Global collapse of frame structures under seismic excitations.
Pacific Earthquake Engineering Research Center, California
Krawinkler
H, Medina R, Alavi B (2003) Seismic drift and ductility demands and their dependence
on ground motions. Eng Struct 25(5):637-653
Kuang
JS, Huang K (2011) Simplified multi-degree-of-freedom model for estimation of
seismic response of regular wall-frame structures. Struct Des Tall Spec Build
20(3):418-432
Lagomarsino
S (1993) Forecast models for damping and vibration periods of buildings. J Wind
Eng Ind Aerod 48(2-3):221-239. doi:10.1016/0167-6105(93)90138-E
Lu
X, Lu XZ, Guan H, Ye LP (2013a) Collapse
simulation of reinforced concrete high-rise building induced by extreme earthquakes.
Earthq Eng Struct Dyn 42(5):705-723
Lu
XZ, Lu X, Guan H, Zhang WK, Ye LP (2013b) Earthquake-induced collapse simulation
of a super-tall mega-braced frame-core tube building. J Constr Steel Res 82:59-71
Lu
X, Lu XZ, Guan H, Ye LP (2013c) Comparison and selection of ground motion intensity
measures for seismic design of super high-rise buildings. Adv Struct Eng 16(7):1249¨C1262
Lu X, Ye LP, Lu XZ, Li MK, Ma XW (2013d) An improved
ground motion intensity measure for super high-rise buildings. Sci China Technol
Sc 56(6):1525¨C1533
Lu
X, Lu XZ, Sezen H, Ye LP (2014a) Development
of a simplified model and seismic energy dissipation in a super-tall building.
Eng Struct 67:109-122
Lu
XZ, Han B, Hori M, Xiong C, Xu Z (2014b) A coarse-grained parallel approach
for seismic damage simulations of urban areas based on refined models and GPU/CPU
cooperative computing. Adv Eng Softw 70:90-103
Lu
XZ, Li MK, Guan H, Lu X, Ye LP (2015) A comparative case study on seismic design
of tall RC frame©\core©\tube
structures in China and USA. Struct Des Tall Spec Build 24(9):687-702
MAE Center (2006) Earthquake risk assessment
using MAEviz 2.0: a tutorial. Mid-America Earthquake Center, University of Illinois
at Urbana-Champaign, Urbana-Champaign, Illinois
Miranda E, Taghavi S (2005) Approximate floor
acceleration demands in multistory buildings. I: Formulation. J Struct Eng 131(2):203-211
MOHURD (2010a) Technical specification for
concrete structures of tall building (JGJ3-2010). Ministry of Housing and Urban-Rural
Development of the People¡¯s Republic of China, Beijing
MOHURD (2010b) Code for seismic design of
buildings (GB50011-2010). Ministry of Housing and Urban-Rural Development of
the People¡¯s Republic of China, Beijing
MOHURD (2010c) Code for design of concrete
structures (GB50010-2010). Ministry of Housing and Urban-Rural Development of
the People¡¯s Republic of China, Beijing
Nakashima M, Ogawa K, Inoue K (2002) Generic
frame model for simulation of earthquake responses of steel moment frames. Earthq
Eng Struct Dyn 31(3):671-692
Paulay T, Priestley MJN (1992) Seismic design
of reinforced concrete and masonry buildings. John Wiley, New York
PEER (2012) PEER NGA Database. Pacific
Earthquake Engineering Research Center. http://peer.berkeley.edu/nga/. Accessed
on 2 October 2015
Reinoso E, Miranda E (2005) Estimation
of floor acceleration demands in high-rise buildings during earthquakes. Struct Des Tall Spec Build 14(2):107-130
Ren
PQ, Li Y, Guan H, Lu XZ (2015) Progressive collapse resistance of two typical
high-rise RC frame shear wall structures. ASCE J Perform Constr Facil 29(3):
04014087. doi: 10.1061/(ASCE)CF.1943-5509.0000593
Reyners M (2011) Lessons from the destructive
Mw 6.3 Christchurch, New Zealand, earthquake. Seismol Res Lett 82(3):371-372
Steelman JS, Hajjar JF (2009) Influence of
inelastic seismic response modeling on regional loss estimation, Eng Struct
31(12):2976-2987
Su RKL, Lam NTK, Tsang HH (2008) Seismic drift
demand and capacity of non-seismically designed concrete buildings in Hong Kong.
Electron J Struct Eng 8:110-121
Tremblay R, L¨¦ger P, Tu J (2001) Inelastic
seismic response of concrete shear walls considering P-delta effects. Can J
Civ Eng 28(4):640-655
Wang MF, Zhou XY (2002) A practical method
for nonlinear seismic responses of RC frame wall structure. China Civil Engineering
Journal 35(6):32-38 (in Chinese)
Wikipedia
(2012) List of tallest buildings in Christchurch. http://en.wikipedia.org/wiki/List_of_tallest_buildings_in_Christchurch.
Accessed on 2 October 2015
Wilkinson S, Grant D, Williams E, Paganoni
S, Fraser S, Boon D, Mason A, Free M (2013) Observations and implications of
damage from the magnitude Mw 6.3 Christchurch, New Zealand earthquake of 22
February 2011. Bull Earthquake Eng 11(1):107-140
Williams SS (2014) Modernizing the system
hierarchy for tall buildings: a data-driven approach to system characterization.
Master dissertation, University of Notre Dame, Notre Dame, Indiana
|



 (3
(3 (4
(4