Acknowledgements
The authors would like to acknowledge the financial supports of the
National Natural Science Foundation of China (Nos. 11272181, 51261120377),
the Specialized Research Fund for the Doctoral Program of Higher Education
of China (No. 20120002110080), and the Tsinghua University Initiative Scientific
Research Program (Project No. 2014z09099). The authors are also grateful for
Prof. Quan Gu for his help in adding the source code of this new element into
OpenSees.
References
Bao, Y. and Kunnath, S. K. [2010] ¡°Simplified progressive collapse
simulation of RC frame-wall structures,¡± Engineering Structures 32(10), 3153-3162.
Batoz, J. L. and Tahar, M. B. [1982] ¡°Evaluation of a new quadrilateral
thin plate bending element,¡± International Journal for Numerical Methods in
Engineering 18(11), 1655-1677.
Belytschko, T. and Leviathan, I. [1994] ¡°Physical stabilization of
the 4-node shell element with one point quadrature,¡± Computer Methods in Applied
Mechanics and Engineering 113(3), 321-350.
Belytschko, T., Liu, W. K., Moran, B. and Elkhodary, K. [2013] Nonlinear
finite elements for continua and structures. John Wiley & Sons.
Cardoso, R. P. R.,
Yoon, J. W., and Valente, R. A. F. [2006] ¡°A new approach
to reduce membrane and transverse shear locking for one-point quadrature shell elements: linear formulation,¡± International
Journal for Numerical Methods in Engineering 66(2), 214-249.
Chen, Q. and Qian, J. R. [2005] ¡°Static elasto-plastic analysis of
RC shear walls with one row opening,¡± Chinese Journal of Computational Mechanics
22(1), 13-19. [in Chinese]
Chen, X. W., Han, X. L., Jack, C., Lin, S.Y. and Mao, G.N. [2008] ¡°Dynamic
inelastic numerical simulation for a shaking table test of a full scale steel
moment frame structure based on OpenSEES,¡± Proc. of the 14th World Conference
on Earthquake Engineering, Beijing, China.
Chen, Y. T. and Lu, X. L. [2003] ¡°Seismic behavior of coupled shear
walls-experiment and theoretical analysis,¡± Journal of Building Structures
24(4), 25-34. [in Chinese]
Chopra, A. K., and Goel, R. K. [2002] ¡°A modal pushover analysis procedure
for estimating seismic demands for buildings,¡± Earthquake Engineering &
Structural Dynamics 31(3), 561-582.
CMC. [2010] Code for Seismic Design of Buildings (GB50011-2010), China
Ministry of Construction; China Architecture and Building Press, Beijing,
China. [in Chinese]
Dassault Syst¨¨mes Simulia Corp.. [2009] Abaqus Theory Manual. Abaqus
6.9 HTML Documentation. http://abaqusdoc.ucalgary.ca/v6.9/books/stm/default.htm
Dvorkin, E. N. and Bathe, K. J. [1984] ¡°A continuum mechanics based
four-node shell element for general non-linear analysis,¡± Engineering computations
1(1), 77-88.
Fajfar, P. [2000] ¡°A nonlinear analysis method for performance-based
seismic design,¡± Earthquake spectra 16(3), 573-592.
Fan, H., Li, Q. S., Tuan, A. Y. and Xu, L. [2009] ¡°Seismic analysis
of the world¡¯s tallest building,¡± Journal of Constructional Steel Research
65, 1206-1215.
FEMA. [2000] ¡°Recommended seismic design criteria for new steel moment
frame buildings,¡± Publ. No. 350, Washington, D.C.
Fischinger, M., Rejec, K. and Isaković, T. [2012] ¡°Modeling inelastic
shear response of RC walls,¡± Proc. of the 15th World Conference on Earthquake
Engineering, Lisboa.
Horrigmoe, G. and Bergan, P. G. [1978] ¡°Nonlinear analysis of free-form
shells by flat finite elements,¡± Computer Methods in Applied Mechanics and
Engineering 16, 11-35.
Jan, T. S., Liu, M. W., and Kao, Y. C. [2004] ¡°An upper-bound pushover
analysis procedure for estimating the seismic demands of high-rise buildings,¡±
Engineering Structures 26(1), 117-128.
Jalayer, F. [2003] ¡°Direct probabilistic seismic analysis: implementing
nonlinear dynamic assessments,¡± PhD. Dissertation, Department of Civil Engineering,
Stanford University.
Krawinkler, H., and Seneviratna, G. [1998] ¡°Pros and cons of a pushover
analysis of seismic performance evaluation,¡± Engineering structures 20(4),
452-464.
Lignos, D. G., Chung, Y., Nagae, T. and Nakashima, M. [2011] ¡°Numerical
and experimental evaluation of seismic capacity of high-rise steel buildings
subjected to long duration earthquakes,¡± Computers & Structures 89(11),
959-967.
Long, Y. Q., Cen, S. and Long, Z. F. [2009] Advanced finite element
method in structural engineering, Tsinghua University Press.
Lin, K. Q., Xie, L. L., Lu, X. Z. and Ye, L. P. [2015] ¡°Earthquake-induced
collapse simulation of a super-long span cable-stayed bridge based on an open
source FE program,¡± Proc. of IABSE Conference-Structural Engineering: Providing
Solutions to Global Challenges, Geneva, Switzerland.
Lu, X., Lu, X. Z.,
Zhang, W. K. and Ye, L. P. [2011] ¡°Collapse simulation of a super high-rise
building subjected to extremely strong earthquakes,¡± Science China Technological
Sciences 54(10), 2549-2560.
Lu,
X., Lu, X. Z., Guan, H. and Ye, L. P. [2013a] ¡°Collapse simulation of reinforced
concrete high-rise building induced by extreme earthquakes,¡± Earthquake Engineering
& Structural Dynamics 42(5), 705-723.
Lu, X. Z., Lu, X., Guan, H., Zhang, W.K. and Ye, L. P. [2013b] ¡°Earthquake-induced
collapse simulation of a super-tall mega-braced frame-core tube building,¡±
Journal of Constructional Steel Research 82, 59-71.
Lu, X. Z.,
Li, M. K., Guan, H., Lu, X. and Ye, L. P. [2015a] ¡°A comparative case study
on seismic design of tall RC frame-core-tube structures in China and USA,¡±
The Structural Design of Tall and Special Buildings 24(9), 687-702.
Lu,
X. Z., Xie, L. L., Guan, H., Huang, Y. L. and Lu, X. [2015b] ¡°A shear wall
element for nonlinear seismic analysis of super-tall buildings using OpenSees,¡±
Finite Elements in Analysis and Design 98, 14-25.
Lu,
X., Lu, X. Z., Guan, H., and Xie, L. L. [2016] ¡°Application of earthquake-induced
collapse analysis in design optimization of a supertall building,¡± The Structural
Design of Tall and Special Buildings 25(17), 926¨C946. DOI: 10.1002/tal.1291.
Lu, Y., Panagiotou, M. and Koutromanos, I. [2014] ¡°Three-dimensional
beam-truss model for reinforced-concrete walls and slabs subjected to cyclic
static or dynamic loading,¡± Pacific Earthquake Engineering Research Center,
Los Angeles, California.
MacNeal, R. H. and Harder, R. L. [1985] ¡°A proposed standard set of
problems to test finite element accuracy,¡± Finite Elements in Analysis and
Design 1(1), 3-20.
Madenci, E. and Barut, A. [1994] ¡°A free-formulation-based flat shell
element for non-linear analysis of thin composite structures,¡± International
Journal for Numerical Methods in Engineering 37(22), 3825-3842.
Moehle, J., Bozorgnia, Y., Jayaram, N., Jones, P., Rahnama, M., Shome,
N., Tuna, Z., Wallace, J., Yang, T., and Zareian, F. [2011] ¡°Case Studies
of the Seismic Performance of Tall Buildings Designed by Alternative Means,¡±
Pacific Earthquake Engineering Research Center, University of California,
Berkeley, California, USA, July.
MSC Software. [2007] Marc 2007 r1 User's Guide, MSC Software, Santa
Ana, CA.
NVIDIA. [2014a] CuSP Home Page. http://cusplibrary.github.io/.
NVIDIA. [2014b] CUDA C programming guide, http://docs.NVIDIA.com/cuda/pdf/CUDA_C_Programming_Guide.pdf;
Date accessed: May 2016.
Park, H. C., Cho, C. and Lee, S. W. [1995] ¡°An efficient assumed strain
element model with six DOF per node for geometrically non-linear shells,¡±
International Journal for Numerical Methods in Engineering 38(24), 4101-4122.
PEER. [2014] Subversion Repositories, http://opensees.berkeley.edu/WebSVN/listing.php?repname=OpenSees&path=%2Ftrunk%2FSRC;
Date accessed: May 2016.
Podio-Guidugli P. [1989] ¡°An exact derivation of the thin plate equation,¡±
Journal of Elasticity 22(2-3), 121-133.
Riahi, H.T., Amouzegar, H., and Falsafioun, M. [2015] ¡°Seismic collapse
assessment of reinforced concrete moment frames using endurance time analysis,¡±
The Structural Design of Tall and Special Buildings 24(4), 300-315.
Shi, G. and Voyiadjis, G. Z. [1991] ¡°Efficient and accurate four-node
quadrilateral C0 plate bending element based on assumed strain fields,¡± International
Journal for Numerical Methods in Engineering 32(5), 1041-1055.
Villaverde, R. [2007] ¡°Methods to assess the seismic collapse capacity
of building structures: State of the art,¡± Journal of Structural Engineering,
ASCE, 133(1), 57-66.
Xie, L. L., Lu, X.
Z., Guan, H. and Lu, X. [2015] ¡°Experimental study and numerical model calibration
for earthquake-induced collapse of RC frames with emphasis on key columns,
joints and overall structure,¡± Journal of Earthquake Engineering 19(8), 1320-1344.
Xu, Y. and Long, Y. Q. [1993] ¡°Quadrilateral membrane element with
vertex rotational freedom from generalized compatible condition,¡± Engineering
Mechanics 10(3), 27-36. [in Chinese]
Xu,
Z., Lu, X. Z., and Law, K. H. [2016] ¡°A computational framework for regional
seismic simulation of buildings with multiple fidelity models,¡± Advances in
Engineering Software 99, 100-110.
Zhang, H. M. [2007] ¡°Study on the performance-based seismic design
method for shear wall structures,¡± Ph.D. thesis, Tongji University, Shanghai,
China. [in Chinese]
Zhang, Q., Lu, M. and Kuang, W. Q. [1998] ¡°Geometric nonlinear analysis
of space shell structures using generalized conforming flat shell elements-for
space shell structures,¡± Communications in Numerical Methods in Engineering
14(10), 941-957.
Zhang, Y. X. and Yang, C. H. [2006] ¡°A family of simple and robust
finite elements for linear and geometrically nonlinear analysis of laminated
composite plates,¡± Composite Structures 75(1), 545-552.
Appendix
A. GPU-based Matrix Solvers in OpenSees
A new GPU-based parallel solver for the sparse systems of equations
(SOEs) is developed and added to OpenSees, namely CuSP solver [Xu et al., 2016]. The matrix algorithm of CuSP solver is based on CuSP [NVIDIA, 2014a],
a GPU-accelerated numerical library for the sparse SOEs developed by Compute
Unified Device Architecture (CUDA) [NVIDIA, 2014b]. The CuSP solver is developed
based on the following rules:
(1)
The iterative algorithms (i.e., the conjugate gradient (CG) algorithm,
Bi-CG algorithm and generalized minimal residual (GMRES) algorithm) are used
to maximize the parallel computing ability of the GPU.
(2)
The Solver class (corresponding to the LinearSOESolver class
of OpenSees) and the solving function are designed separately. The Solver
class is designed inheriting the LinearSOESolver class, to improve
the compatibility of the solver.
(3)
The kernel algorithm of CuSP solver is packaged in the form of a dynamic-link
library (DLL), which is convenient to be updated without changing the framework
of OpenSees.
Figure A.1 illustrates the specific solving process of CuSP solvers.
The matrix is integrated in CPU, and then copied into the graphics memory
to perform the parallel computation. Finally, the results are returned into
CPU for subsequent computation.
The corresponding source codes of CuSP solver are available at the
website of OpenSees [PEER, 2014].
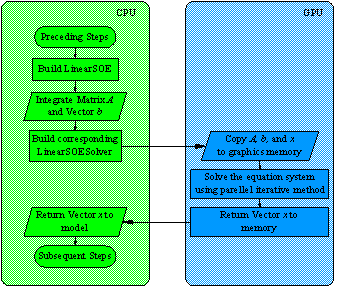
Figure A.1.
Flow chart of GPU-based solvers for the sparse SOEs
Appendix
B. Command lines to implement the multi-layered shell
element and NLDKGQ element
The two-dimensional concrete material is introduced to the
model through the following command lines as
|
nDMaterial PlaneStressUserMaterial
$matTag 40 7 $fc $ft $fcu $epsc0
$epscu $epstu $stc
|
|
$matTag
|
Integer tag identifying material
|
|
$fc
|
Concrete compressive strength (positive)
|
|
$ft
|
Concrete tensile strength (positive)
|
|
$fcu
|
Concrete ultimate strength (negative)
|
|
$epsc0
|
Concrete strain at maximum strength (negative)
|
|
$epscu
|
Concrete strain at ultimate strength (negative)
|
|
$epstu
|
Ultimate tensile strain (positive)
|
|
$stc
|
Shear retention factor
|
|
nDMaterial PlateFromPlaneStress $newmatTag
$matTag $OutofPlaneModulus
|
|
$newmatTag
|
New integer tag
identifying material deriving from pre-defined PlaneStressUserMaterial
|
|
$matTag
|
Integer tag identifying
PlaneStressUserMaterial
|
|
$OutofPlaneModulus
|
Out-of-plane shear
modulus
|
The reinforcing steel material for the multi-layered shell element
is introduced to the model through the following command line as
|
nDMaterial PlateRebar $newmatTag
$matTag $sita
|
|
$newmatTag
|
New integer tag
identifying material deriving from pre-defined uniaxial steel material
|
|
$matTag
|
Integer tag identifying
uniaxial steel material
|
|
$sita
|
Define the angle
of steel layer, 90¡ã (longitudinal steel), 0¡ã
(transverse steel)
|
The multi-layered shell section is defined through
the following command line as
|
section LayeredShell $sectionTag
$nLayers $matTag1 $thickness1 ¡ $matTagn $thicknessn
|
|
$sectionTag
|
Unique tag among sections
|
|
$nLayers
|
Total numbers of layers
|
|
$matTag1
|
Material tag of first layer
|
|
$thickness1
|
Thickness of first layer
|
|
¡
|
|
|
$matTagn
|
Material tag of last layer
|
|
$thicknessn
|
Thickness of last layer
|
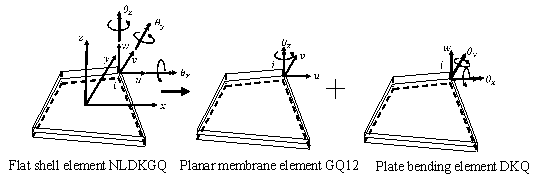
The NLDKGQ shell element is defined through the following command line
as
|
element
ShellNLDKGQ $eleTag $iNode $jNode $kNode $lNode $secTag
|
|
$eleTag
|
Unique element
object tag
|
|
$iNode $jNode $kNode $lNode
|
Four nodes defining
element boundaries, input in clockwise or counter-clockwise order
around the element.
|
|
$secTag
|
Tag associated
with previously-defined SectionForceDeformation object.
|
Address correspondence to Xinzheng Lu, Department of Civil
Engineering, Tsinghua University, Beijing, P.R. China. E-mail: luxz@tsinghua.edu.cn
|
![]() (1)
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)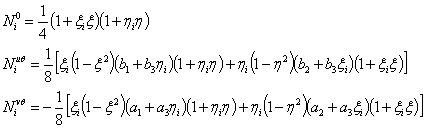 (6)
(6)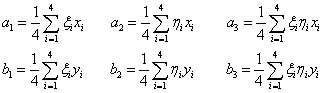 (7)
(7)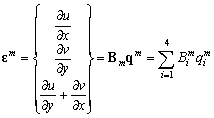 (8)
(8) (9)
(9)![]() (10)
(10)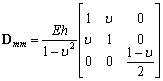 (11)
(11) 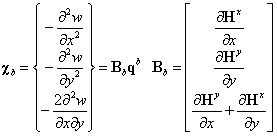 (12)
(12)![]() (13)
(13) (14)
(14)![]() (15)
(15)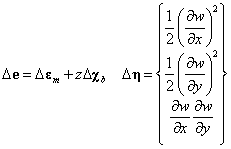 (16)
(16)![]() (17)
(17)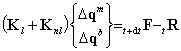 (18)
(18) (19)
(19) (20)
(20)![]() is composed of variables corresponding to the internal force vector
of the membrane element at time t (Equation 22).
is composed of variables corresponding to the internal force vector
of the membrane element at time t (Equation 22).![]() (21)
(21)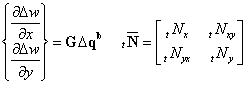 (22)
(22) (23)
(23) (24)
(24) (25)
(25)