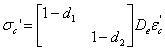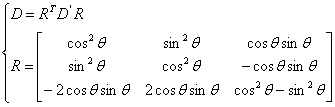2 Multi-layer shell element model for shear walls
2.1 Theoretical background of multi-layer shell element model
The multi-layer shell formulation [1] is implemented in OpenSees using the ¡°ShellMITC4¡± element, which is a four-node shell element based on the theory of mixed interpolation of tensorial components (MITC) proposed by Dvorkin et al. [19].
|
|
|
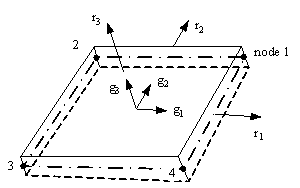
Fig. 1. Local Cartesian coordinate system |
Fig. 1 illustrates the local coordinate system adopted for the shell element. Vector r1 extends from the midpoint of Nodes 2 and 3 to the midpoint of Nodes 1 and 4. Vector r2 extends from the midpoint of Nodes 3 and 4 to the midpoint of Nodes 1 and 2. The Gram-Schmidt orthonormalization is then adopted to adjust Vector r2. Finally, Vector r3 is determined as the cross product of Vectors r1 and r2 following the right hand rule. Vectors g1, g2 and g3 are obtained through vector unitization of Vector r1, orthogonal Vector r2 and Vector r3, respectively. The strains and curvatures at the in-plane integration points are obtained from the interpolation of the nodal displacements and rotations. When large deformations are taken into consideration, the coordinate system is updated based on the current coordinates of the nodes.
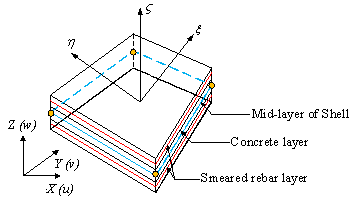
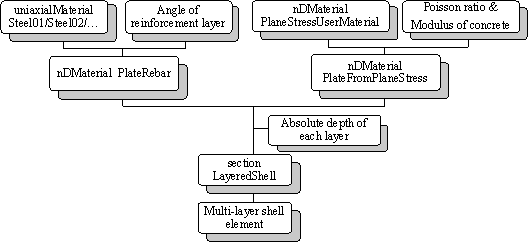
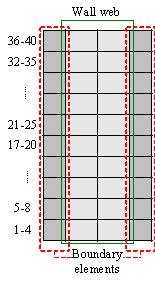
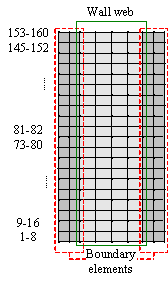
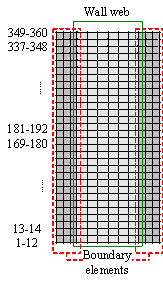
For each of the in-plane integration points, a layered/composite integrated section is then implemented to account for the nonlinear behavior of reinforced concrete (RC). The layered element simplifies the three-dimensional nonlinear behavior of the shear walls into a shell situation by discretizing them into several fully-bonded layers in the thickness direction. Different material properties and thicknesses can be assigned to each layer according to the size of the wall and the distribution of reinforcing bars, as illustrated in Fig. 2. The bars are smeared into one or more orthotropic layers according to their physical location and direction, as shown in Fig. 3. The stresses over a layer thickness are assumed to be consistent with those at the mid-surface of that layer. Therefore, if the shear wall is subdivided into sufficient number of layers, the multi-layer shell element can reasonably simulate the actual stress distribution over the thickness of the wall [20-21].
|
|
|
Fig. 2. Multi-layer shell element |
|
|
|
Fig. 3. Distribution of the rebar layer |
The nonlinear behavior of concrete cracking, crushing and aggregate interlocking is incorporated in the planar concrete constitutive model. For steel reinforcement, the nonlinear behavior of yielding and the Bauschinger effect are taken into consideration in its uniaxial model.
In the multi-layer shell element, the axial strains and curvature of the middle layer are initially calculated; the strains of each layer are then obtained based on the plane-section assumption. The stresses of each integration point on each layer are subsequently calculated in accordance with the constitutive model of the corresponding layer. Lastly, the internal forces are calculated using the standard numerical integration method.
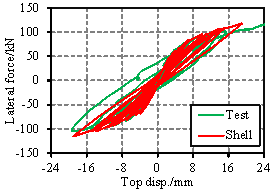
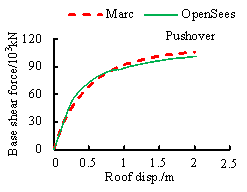
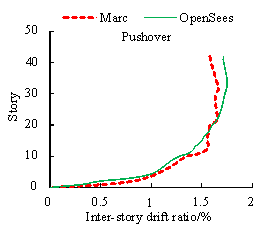
The multi-layer shell element has been proven to be a suitable model that can well capture the coupled in-plane/out-of-plane bending as well as the in-plane direct shear and coupled bending/shear behavior of the RC shear walls [1, 6, 20-22].
2.2 Two-dimensional material constitutive model
Concrete is assumed to be in a state of planar stress in the multi-layer shell element. An appropriate, reliable and robust two-dimensional concrete constitutive model is required to cater for the complicated mechanical behavior of shear walls and core tubes induced by an earthquake. The analytical model for concrete proposed in this research is based on the concept of damage mechanics and the smeared crack model. Cracks are assumed to form when the principal tensile stress exceeds the specified concrete tensile strength. Once cracking occurs, concrete is then treated as an orthotropic material. The shear stiffness deterioration (in terms of the reduced shear moduli obtained by multiplying the shear retention factor) is incorporated due to the effects of aggregate interlocking. Being simple in formulation, this analytical model also demonstrates a good stability in computation [21, 22].
The constitutive equation (Eq. 1) of concrete is expressed as follows:
|
|
(1) |
where sc¡¯ and ec¡¯ represent the stress and strain tensors, respectively, in the principal stress coordinate system before cracking or in the crack coordinate system after cracking. De is the elastic constitutive matrix, and d1 and d2 are the damage parameters, which can be respectively calculated by the damage evolution curves under tension as recommended by Løland [23] and under compression as suggested by Mazars [24].
After cracking, the relationship between the shear stress t and shear strain g in the crack coordinates is as follows:
|
|
(2) |
where G is the elastic shear modulus and b is the shear retention factor to account for the shear stiffness deterioration after cracking occurs [25].
Both Eqs. 1 and 2, formulated with either the principal stress coordinate or the crack coordinate, must be transformed to a global coordinate system [26] following Eq. 3.
|
|
(3) |
where D and D¡¯ are the constitutive matrices in the global and local coordinates, respectively. R is the transformation matrix and q is the angle between the global and local coordinates.
The reinforcing bars are simulated as smeared steel layers of equivalent thicknesses. The material model for reinforcing steel, designated as PlateRebar, is derived from the uniaxial materials for rebars [15] in conjunction with their corresponding angles. Detailed information can be found in Appendix A.