Collapse simulation of a super high-rise building subjected to extremely strong earthquakes. Sci China Tech Sci, 2011, 54(10): 2549-2560.

1 Introduction

Since the completion of the world’s first super high-rise building, Taipei 101 (which has a total height exceeding 500 m) in 2004, a new wave of competition with respect to the design and construction of super high-rise buildings has started. For example, the Burj Khalifa, 828 m high, located in Dubai and completed in 2010, is currently the tallest building in the world. With the rapid economic development of China, the development of super high-rise buildings is also very rapid. Currently, there are more than 3 super high-rise buildings higher than 600 m under construction in mainland China, making it the world champion in quantity. Statistical data from the Council on Tall Buildings and Urban Habitat (CTBUH) in 2010 (http://buildingdb.ctbuh.org/) indicated that there were approximately 120 super high-rise buildings higher than 300 m either completed or under construction in the world at the beginning of 2010. These buildings are mainly located in China, the Arab Emirates and the USA (there are 47 in China, including 3 in Taipei; 28 in the Arab Emirates and 18 in the USA). Super high-rise buildings promote the development of new structural systems and novel mega-structural components. However, it is difficult to study these new systems and components using traditional experimental research methods. Therefore, the seismic safety of super high-rise buildings and, in particular, their collapse resistances to extreme ground motions, has become an important and urgent research topic.

The shaking table test is a traditional method used to study or evaluate the global seismic performance of new structural systems. In 2002, Lu and Zhu conducted a 1:50-scale shaking table test of a reinforced concrete (RC) tube-in-tube high-rise building 166 m in height and evaluated its seismic safety in the Design Earthquake and the Maximum Considered Earthquake in Intensity 7 regions ^[¹^]. In 2006, a 1:50-scale shaking table test of the Shanghai World Financial Center was conducted by Zou and Lu ^{[2
]}, and they analyzed the dynamic properties and seismic responses when the building was subjected to the Frequently Occurring Earthquake, the Design Earthquake, and the Maximum Considered Earthquake in Intensity 7 regions and the Maximum Considered Earthquake in Intensity 8 regions. In 2006, Li and Lam also conducted a 1:20-scale shaking table test of a high-rise building (120 m) in Hong Kong ^{[3 ]}. In 2010, Mao and Lu performed a 1:50-scale shaking table test of Shanghai Tower and analyzed the seismic performances when the building was subjected to the Frequently Occurring Earthquake, the Design Earthquake, and the Maximum Considered Earthquake in Intensity 7 regions and the Maximum Considered Earthquake in Intensity 7.5 regions ^{[4 ]}. However, none of the structures in these shaking table tests collapsed, i.e., it was difficult to understand the collapse process and corresponding mechanism from these shaking table tests. In 2007, a collapse test of a 1:4-scale 3-story, 1-span RC frame was performed by Huang and Gu ^{[5
]}. In 2008, a collapse test of a 4-story steel moment resisting frame was conducted using the three-dimensional shake table facility of E-Defense to evaluate the structural and functional performance of the building under design-level ground motions ^{[6 ~7
]}. The safety margin against collapse subjected to extremely strong ground motions was also evaluated. The research outcomes indicated that the failure mode of the building when subjected to 100% Takatori ground motion records was a weak story failure mode in the first story, which was induced by deterioration in the strength of columns due to local buckling at the top and bottom of the columns. In 2009, van de Lindt et al. performed a collapse test of a full-scale, 6-story, light-frame wooden building on the shaking table of E-Defense ^{[8
]}. It demonstrated that the wooden structure had an excellent seismic performance with only slight damage caused even subjected to an earthquake of 2,500-year return period. Wu and Kuo also conducted a collapse test of a non-ductile concrete frame using a shaking table in 2009 ^{[9 ]}. Although great progress has been achieved in researching earthquake-induced collapse resistance using shaking table tests, only scaled multi-story buildings or full-scale low rise buildings can be tested on shaking tables due to the limited capacity of the shaking table facility and experimental safety considerations. It is very difficult to study the seismic collapse resistances of super high-rise buildings using conventional shaking table tests. In addition, the shaking table test is very expensive.

Alternatively, numerical simulation is gradually playing an important role in the study of seismic performance and collapse resistance. In 2001, based on the finite element (FE) code of LS-DYNA, Lu developed an FE model to simulate the collapse process of the World Trade Center in New York, which had been impacted by aircraft, and explained the main reasons for the progressive collapse ^{[10
]}. In 2004, Pan and Brownjohn presented a numerical study on the dynamic responses of the tallest building in Singapore and compared the FE results with 21 field measurements of the structural response to far-field ground motions. The predicted roof displacement of the structure agreed well with the field observations ^{[11 ]}. In 2006, Pekau and Cui developed a distinct element method (DEM) program to simulate the earthquake-induced collapse of a 20-story, 3-span precast-panel shear wall structure. The results indicated that if the design of this precast-panel shear wall satisfies seismic requirements, it will automatically meet the ductility demands of progressive collapse prevention ^{[12 ]}. In 2007, Mattern and Blankenhorn compared the progressive collapse processes of a 3-span frame as predicted using finite-element and rigid-body methods. The study showed that the rigid-body method gave similar results to the finite-element method at a lower computational cost ^{[13
]}. In 2009, Fan and Li constructed an FE model of Taipei 101 and analyzed its seismic performance. Their research indicated that the super high-rise building, which has a mega-frame system, has sufficient safety margins and it satisfies the design requirements for the Maximum Considered Earthquake ^{[14
]}.

Many numerical simulations on the seismic behavior of high-rise buildings have been reported in the literature, but most of these studies are conventional elasto-plastic analyses. The entire process of simulating structural seismic response, including yielding, hardening and collapse, has rarely been reported, especially for super high-rise buildings. Several important problems need to be solved in the collapse simulation of super high-rise buildings, including the modeling of complex structures, solving of extreme nonlinearity and large-scale computation. Therefore, this has become an important frontier of earthquake engineering.

With the support of the Key Research Plan “Dynamic Disaster Evolution of Important Engineering Structures” of the National Natural Science Foundation of China (NSFC), this paper builds up a nonlinear finite element model of the tallest building in China, Shanghai Tower (632 m). The dynamic characters of this building are analyzed, and the possible failure modes and collapse processes due to earthquakes are predicted, as well as the corresponding collapse mechanism. This work will be helpful in collapse prevention and the seismic design of super high-rise buildings.

2 Overview of Shanghai Tower

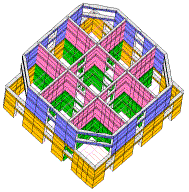
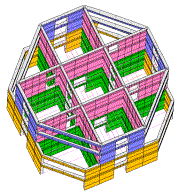
Shanghai Tower, located in Lujiazui, Shanghai, is a multi-functional office building (as shown in Figure 1). The total height of the main tower is 632 m, and the structural height is 580 m. This building contains 124 stories. A hybrid lateral-force-resisting system (as shown in Figure 2) referred to as “mega-column/core-tube/outrigger” was adopted for the main tower. The details of this system are described briefly as follows:

(1) The main part of the core-tube is a 30 m by 30 m square RC tube. The thickness of the flange wall of the tube at the bottom is 1.2 m, and the thickness decreases with the height of the tube and reduces to 0.5 m at the top. Similarly, the thickness of the web wall decreases from 0.9 m at the bottom to 0.5 m at the top. According to the architectural functional requirements, the four corners of the core-tube are gradually removed above Zone 5. Finally, the core-tube becomes X-shaped at the top ^{[4
, 15 ]}.

(2) The mega-column system consists of 12 shaped-steel reinforced concrete columns with a maximum cross-sectional dimension of 5,300 mm×3,700 mm ^{[15 ]}. 8 mega-columns extend from the bottom to the top of the building, and the section size gradually reduces to 2,400 mm×1,900 mm at the top. The remaining 4 columns are located at each corner and only extend from the ground floor to Zone 5.

(3) The outrigger system, located at the mechanical stories, consists of circle trusses and outriggers with a total height of 9.9 m. All of the components of the outriggers are composed of H-shaped steel beams.

Figure 1 The location of the 3 super high-rise buildings in Shanghai (From: www.eastday.com)

Figure 1 The location of the 3 super high-rise buildings in Shanghai (From: www.eastday.com)

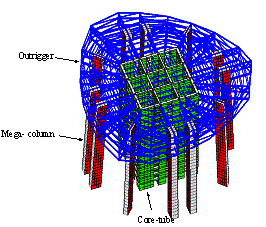
Figure 2 Sketch of lateral-force-resisting system of Shanghai Tower

Figure 2 Sketch of lateral-force-resisting system of Shanghai Tower

3 Finite element model

Based on the general-purpose finite-element program MSC.MARC, which has an excellent nonlinear computational capacity, the nonlinear FE model of Shanghai Tower is built up using the material constitutive laws, element models and elemental failure criteria proposed by Tsinghua University. Thus, the special requirements of the collapse simulation of super high-rise buildings subjected to strong earthquakes, such as the modeling of complex structures, solving of extreme nonlinearity and large-scale computation, are satisfied.

Four element types are used in this model: the spatial beam elements used for the external frames and outriggers, the multi-layer shell elements used for the shear walls and the mega-columns, the truss elements used for the rebar and the shaped-steels, and membrane elements for the floor slabs. The details are described in the following subsections.

3. 1 Material constitutive laws

In this work, the material-based constitutive law was adopted for all components to accurately simulate the nonlinear behavior and failure under the complex stress state (i.e., the coupled axial force, bending moment and shear force) during the collapse process ^{[16
]}. The main construction materials used in Shanghai Tower are concrete and steel. The von Mises yielding criterion and the isotropic hardening rule were adopted for the concrete, and the normalized equivalent uniaxial compressive stress-strain relationship ^{[17
]} is shown in Figure 3. The strengthening branch was based on the model proposed by Hongnestad. The softening branch used was a straight line with 0.3f_c residual strength, where f_c is the peak strength. The smeared crack model was adopted for concrete under tension^{[17 ]}. Similarly, the von Mises yielding criterion-based plastic constitutive model was adopted for the steel. The model proposed by Wang et al. ^{[18 ]} with four stages (elastic, yield, hardening and post-capping) was adopted for the backbone curve of the stress-strain relationship as shown in Figure 4.

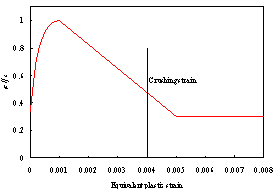
Figure 3 The normalized stress-equivalent plastic strain relationship for concrete in compression

Figure 3 The normalized stress-equivalent plastic strain relationship for concrete in compression

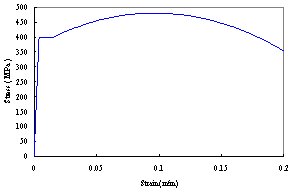
Figure 4 The stress-strain relationship of steel

Figure 4 The stress-strain relationship of steel

3. 2 Core-tube

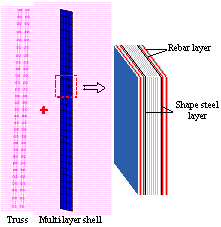
The multi-layer shell element (as shown in Figure 5) proposed by Lu et al. with outstanding nonlinear performance was adopted to model the core-tube, which considers the bending and shear coupling both in-plane and out-plane. Lu et al. have verified the accuracy and efficiency of the multi-layer shell element model for application to shear walls ^{[19
~21 ]}. The FE models of typical core-tubes are shown in Figure 6.

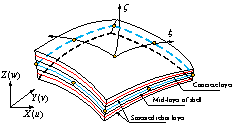
Figure 5 Multi-layer shell element

(a)

(b)

(c)

Figure 6 FE models of typical core-tubes: (a) the core-tube from Zone 1 to Zone 5; (b) the core-tube of the junction of Zone 4 and Zone 5; (c) the core-tube of the junction of Zones 6 and 7

3. 3 Outrigger, external frame and other components

The external frame, outrigger and steel tower at the top are constructed with H-shaped steel beams and simulated using a fiber-beam element model. To ensure computational accuracy, each segment of the cross-section (i.e., the flange and web) is divided into 9 fibers. In total, therefore, there are 27 fibers in each section. The fiber-beam element model has been widely used in the elasto-plastic analysis of earthquake engineering, and its accuracy has been verified for many times ^{[22 ~25
]}.

3. 4 Mega-columns

One of the most interesting components in Shanghai Tower is the mega-column system, which includes 12 mega-columns, among them 8 extend to the top, and the remaining 4 end at Zone 5. These mega-columns are constructed with shaped-steel reinforced concrete, and a typical cross-section is shown in Figure 7 (a). The area of this section is nearly 20 m² and has a steel ratio of 6.22% and a reinforcement ratio of 1.16%. The dimensions of these mega-columns are so large that they go far beyond the general conception of “columns”, and the reinforcement and steel in the columns significantly confine the mechanical behavior of the concrete. Hence, the traditional fiber-beam element model cannot meet the computational accuracy. Meanwhile, the computational workload would be too big if solid elements were adopted for the mega-columns in the analysis of the whole structure. Because few experimental data regarding the mega-columns can be found in the literature, a multi-layer shell element-based simplified model was proposed for the mega-columns to find a balance between computational accuracy and cost, and the parameters of the simplified model were determined based on the detailed FE model of mega-columns with solid elements.

In the detailed FE model, the concrete, shaped-steel and rebar were modeled using hexahedral solid elements, quadrilateral shell elements and truss elements, respectively. In contrast, the simplified model was combined with multi-layer shell elements and truss elements. The concrete, rebar distributed along the Y-direction and the web of the shaped steel were modeled using multi-layer shell elements, while the shaped-steel flange and the rebar distributed along the X-direction were modeled using truss elements. The displacement compatibility among the shell and truss elements was achieved using shared nodes as shown in Figure 7 (c).

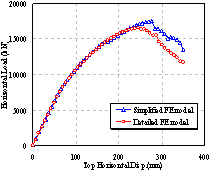
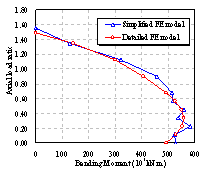
Numerical simulations of the mega-columns under pure compression, pure bending, bending with compression in one direction and bending and compression in the biaxial direction etc. were conducted to evaluate the simplified model. Details of the load cases are shown in Figure 8. Typical results are compared in Figure 9, and further details regarding the comparison can be found in ref.[26 ]. The proposed simplified method can predict the nonlinear behavior of the mega-columns with acceptable tolerance compared to the detailed FE model. In addition, the degree of freedom in the simplified model is much less than that in the detailed model (see the comparison in Table 1). Therefore, the proposed simplified model of the mega-columns can be used in the global structural seismic response analysis.

Table 1 Element and node numbers of detailed and simplified FE models

	Detailed FE model	Simplified FE model
Element number	86563	706
Node number	54542	400

Finally, the complete FE model of Shanghai Tower is shown in Figure 10.

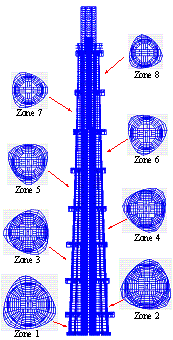
Figure 10 The whole FE model of Shanghai Tower

Figure 10 The whole FE model of Shanghai Tower

3. 5 Failure criteria

Collapse is a very complicated process in which the structural components reach their load capacities and the entire structure changes from a continuum system into discrete parts through structural fracturing and element crushing. This process can be simulated using elemental deactivation technology, where the failed elements are deactivated when a specified elemental-failure criterion is reached. Shell, beam and truss elements are included in the FE model of Shanghai Tower, and different elemental-failure criteria are adopted for different elements. For the multi-layer shell model, each element has at least 11 layers (the number of layers depends on the specific situation of the actual reinforcement), and each layer has 4 Gaussian integration points. If the principal compressive strain at any integration point in a layer (either concrete or steel) exceeds 0.1 or the principal tensile strain exceeds 0.2, the stress and the stiffness of this layer are deactivated, meaning that this layer no longer contributes to the stiffness computation of the whole structure. If all the layers of a shell element are deactivated, then the element is considered fully deactivated from the model. Similarly, for the fiber-beam element model, each element has 27 fibers in its cross section and 2 Gauss integration points along the length. If the equivalent plastic strain at all fibers exceeds the ultimate tensile strain, which is equal to 0.2, then this element is considered to have failed and is fully deactivated from the model. For truss elements, each element has 1 Gauss integration point. If the equivalent plastic strain at the integration point exceeds the ultimate tensile strain of 0.2, then this element is deactivated and removed from the complete model ^{[27
]}.

4 Collapse process and mechanism analysis

After careful design and evaluation, the safety of Shanghai Tower subjected to the Maximum Considered Earthquake has been ensured ^{[15 ]}. However, to further understand the collapse process and mechanism of super high-rise buildings, the intensity of ground motions is scaled until the structure collapses. Although such a large earthquake is unlikely to happen in Shanghai, it will be helpful to understand the mechanical properties of super high-rise buildings given the predicted collapse modes and mechanism.

4. 1 Basic dynamic properties

Before the collapse is simulated, modal analysis is conducted, and the first 30 modes are calculated. The first 9 free vibration periods and modal properties are shown in Table 2. The fundamental period of Shanghai Tower is 9.83 s in direction X and 9.77 s in direction Y, which are both far beyond the range of 6 s specified in the design response spectrum in the Chinese Code for the Seismic Design of Buildings (GB50011-2010) ^{[28 ]}.

4. 2 Seismic collapse subjected to one directional ground motion

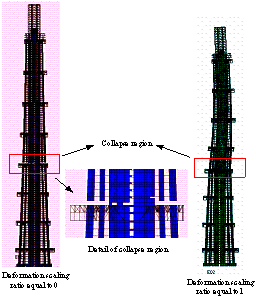
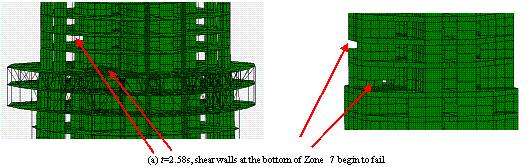
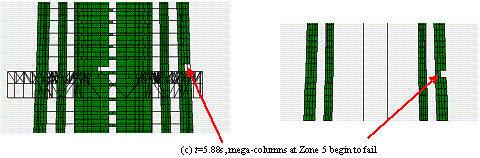
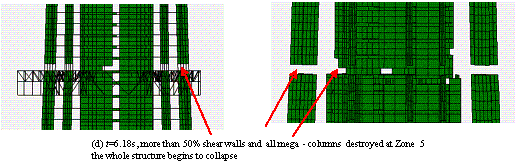
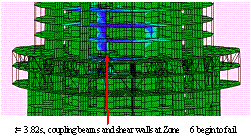
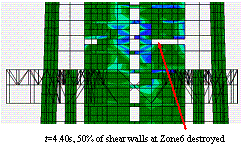
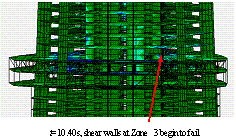
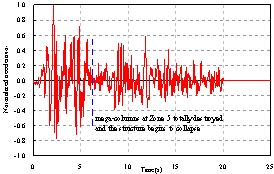
The widely used ground motion recorded at El-Centro station in the USA in 1940 (referred to as “El-Centro” hereafter) was chosen as a typical example of ground motion input. The normalized acceleration time history of the east-west components of El-Centro ground motion and its elastic response spectrum with 5% damping ratio are shown in Figure 11. The peak ground acceleration (PGA) is scaled to 19.6 m/s², which is 6.4 times larger than the actual ground motion intensity (the actual PGA of the El-Centro ground motion was 3.07 m/s²) and then used as input for the FE model in the X direction. Because limited data can be found for the damping ratio of long period structures subjected to strong earthquakes, the 5% damping ratio proposed in Section 5.3.4 of the Specification for the Design of Steel-Concrete Hybrid Structures in Tall Buildings (CECE230:2008) ^{[29 ]} is adopted in the analysis. The final collapse mode is shown in Figure 12(a). The details of the collapse process are clearly shown in Figure 13. First, when t=2.58 s, some coupling beams in the core-tube begin to fail, and the flange wall of the core-tube at the bottom of Zone 7 is crushed. The reason for this crushing is that the layout of the openings in the core-tube changes between Zones 6 and 7, resulting in a sudden change of stiffness and stress concentration. After that, when t=3.90 s, the shear wall at the bottom of Zone 5 begins to fail because the cross section of the core-tube changes from Zone 4 to Zone 5 as shown in Figure 6 (b). When t=5.88 s, more than 50% of the shear walls at the bottom of Zone 5 fail, and the internal forces are redistributed to other components. The vertical and horizontal loads in the mega-columns increase gradually and reach their load capacities. The mega-columns then begin to fail. Finally, when t=6.18 s, the core-tube and mega-columns in Zone 5 are completely destroyed, and the collapse begins to propagate to the entire structure.

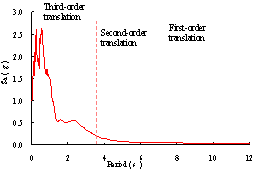
The roof displacement response of Shanghai Tower when subjected to El-Centro ground motion is shown in Figure 14. Former modal analysis indicates that the fundamental periods in the X and Y directions are so long that the corresponding seismic loads are very small. Therefore, the failure of this super high-rise building is dominated by high-order free vibration modes especially the third translational free vibration mode. Therefore, as the structure approaches collapse, the deformation mode is similar to that in the third translational free vibration mode. The mass center of the structure above the failure region does not have very significant displacement, and therefore the main collapse mode of Shanghai Tower is vertical “pan-cake” collapse, rather than lateral overturning.

Figure 11 Normalized acceleration time history and elastic response spectrum with 5% damping ratio of El-Centro

(a)

Figure 11 Normalized acceleration time history and elastic response spectrum with 5% damping ratio of El-Centro

(b)

Figure 11 Normalized acceleration time history and elastic response spectrum with 5% damping ratio of El-Centro: (a) Normalized acceleration time history of east-west component of El-Centro; (b) Elastic response spectrum with 5% damping ratio of El-Centro

Obviously, when subjected to El-Centro ground motion in the X direction, Shanghai Tower is mainly damaged in Zones 5, 6 and 7. Finally, collapse occurs in Zone 5, and the entire structure breaks into two parts. It can be clearly seen that Zone 5 is a potentially weak part, where structural collapse can be initiated. So more attention should be paid to this area during the design. During the collapse process, damage first occurs in the coupling beams, which are the first defense line of the structure against earthquake, and these damages will dissipate some seismic energy. After the failure of the coupling beams, the shear wall of the core-tube and the mega-columns begin to fail. Only when both the shear walls and the mega-columns are damaged to a certain extent in the same section, will the collapse propagate to the entire structure. Therefore, it can be concluded that the initial yield parts obtained using traditional nonlinear dynamic analysis may not coincide with the actual collapse regions. If some improper enhancement measures are performed on those initial yield parts, e.g., the coupling beams, then the energy dissipation capacity of the components may not be fully developed, possibly resulting in an unfavorable design. Therefore, a collapse analysis is an important part of structural seismic response analysis.

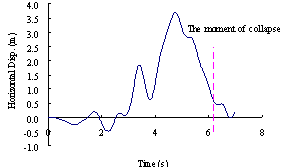
Figure 14 Horizontal roof displacement response of Shanghai Tower subjected to El-Centro

Figure 14 Horizontal roof displacement response of Shanghai Tower subjected to El-Centro (PGA=19.6m/s²）

Figure 15 The distribution of drift ratio between adjacent outriggers

(a)

Figure 15 The distribution of drift ratio between adjacent outriggers

(b)

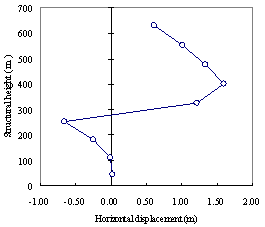
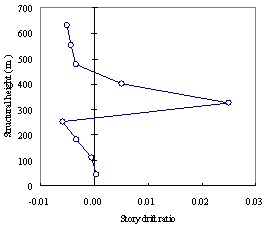
Figure 15 The distribution of drift ratio between adjacent outriggers: (a) distribution of horizontal displacement along the height; (b) distribution of drift ratio between adjacent outriggers

4. 3 Stress-strain relationship of critical components

The collapse process in Figure 13 is the global response of a structure that has been subjected to strong earthquakes. To further study the mechanical behavior of critical components during the structural collapse process, this section focuses on the stress-strain hysteretic relationship of critical components. The typical failure region of Shanghai Tower when subjected to El-Centro ground motion in the X direction is shown in Figure 12(a). Selected elements of critical components in the failed region are displayed in Figure 16. The stress-strain hysteretic relationships of the concrete and steel during the collapse process are shown in Figures 17 to 20.

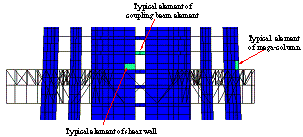
Figure 16 The locations of the typical elements

Figure 16 The locations of the typical elements

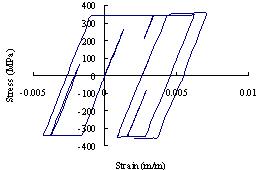
For a typical mega-column, the stress-strain hysteretic relationship of concrete is shown in Figure 17, where compressive stress is negative while tensile stress is positive. Obviously, during the entire collapse process, the stress state of the mega-column is dominated by compression. Finally, the concrete is crushed and the mega-column fails by bending and compression. The failure mode of the coupling beam is shear failure, and the shear force-shear strain hysteretic relationship of a typical coupling beam in the failure state is shown in Figure 18. The stress-strain hysteretic relationships of the core-tube and outriggers are also displayed in Figures 19 and 20.

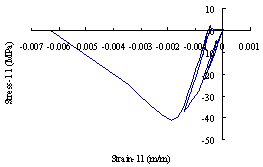
Figure 17 Stress-strain hysteretic of typical failure mega-column

Figure 17 Stress-strain hysteretic of typical failure mega-column

Figure 18 Shear force-strain hysteretic of failure coupling beam

Figure 18 Shear force-strain hysteretic of failure coupling beam

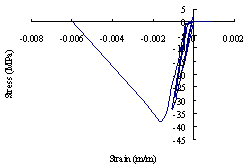
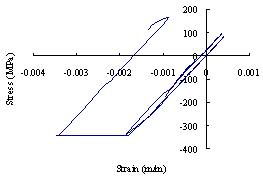
Figure 19 Stress-strain hysteretic of core-tube

(a)

Figure 19 Stress-strain hysteretic of core-tube

(b)

Figure 19 Stress-strain hysteretic of core-tube: (a) stress-strain hysteretic of concrete in core-tube; (b) stress-strain hysteretic of shaped-steel in core-tube

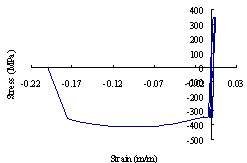
Figure 20 Stress-strain hysteretic of outrigger

(a)

(b)

Figure 20 Stress-strain hysteretic of outrigger: (a) stress-strain hysteretic of failure outrigger; (b) stress-strain hysteretic of undamaged outrigger

5 Other collapse modes

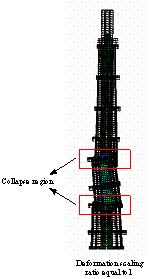
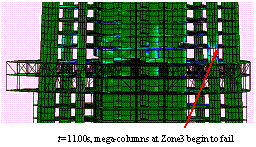
Considering the distinct differences in the spectral responses of different ground motions, the excited vibration modes of structures may differ depending on the ground motion, and the corresponding seismic responses may therefore differ greatly also. For example, if the El-Centro ground motion is selected and input in the X direction, the structure will collapse when the PGA is scaled to 19.6 m/s². However, if Tha-San ground motion, which has many long-period spectral components, is used as input, then the structure will collapse when the PGA is scaled to 3.92 m/s². Furthermore, the input directions of ground motions also strongly influence the collapse modes. If Shanghai artificial ground motion is selected and used as input in both the X and Y directions, then the Shanghai Tower will collapse when the PGA is scaled to 9.8 m/s², and its corresponding collapse mode will be different than those in Figures 12(a) and 13. The collapse mode is shown in Figure 12 (b), and its detailed collapse process is clearly illustrated in Figure 21.