Physics-based simulation and high-fidelity visualization of fire following earthquake considering building seismic damage

Xinzheng Lu ^{1, [*]} , Xiang Zeng ², Zhen Xu ³, and Hong Guan ⁴

¹ Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry, Department of Civil Engineering, Tsinghua University, Beijing 100084, China

² Beijing Engineering Research Center of Steel and Concrete Composite Structures, Department of Civil Engineering, Tsinghua University, Beijing 100084, China

³ School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China

⁴ Griffith School of Engineering, Griffith University, Gold Coast Campus, Queensland 4222, Australia

Journal of Earthquake Engineering, Accepted on June 20, 2017.
DOI: 10.1080/13632469.2017.1351409.

Download PDF Version

This work proposes a framework for the physics-based simulation and high-fidelity visualization of fire following earthquake (FFE) considering building seismic damage. The seismic damage of regional buildings is simulated using multiple degree-of-freedom building models in conjunction with nonlinear time-history analysis. In parallel, a high-fidelity visualization is presented to simulate fire spread and smoke effects. A case study of downtown Taiyuan with 44,152 buildings is performed. The results show that the influence of different ground motions and building seismic resistances on fire ignition and fire spread can be taken into account and that the FFE scene can be displayed realistically.

Keywords: seismic damage simulation of urban region; fire following earthquake; ignition; fire spread; high-fidelity visualization; FDS

1. Introduction

In addition to inducing direct damage, earthquakes can also cause secondary disasters, e.g., fire, landslide, and falling exterior objects [Xu et al., 2016a]. In particular, the statistics of earthquake-induced fatalities in the 20th century show that fire following earthquake (FFE) has caused the highest fatality among various earthquake-induced secondary disasters [Sathiparan, 2015]. In some earthquake events, the damage due to FFE was even more severe than the direct damage of the earthquake. For example, the FFEs of the 1906 San Francisco and 1923 Tokyo earthquakes are considered to be the largest urban fires in peacetime [Scawthorn et al., 2005, Mousavi et al., 2008]. Specifically, in the 1906 San Francisco earthquake, the building damage due to FFE accounted for 80% of the total damage, while in the 1923 Tokyo earthquake, the economic loss due to FFE accounted for 77% of the total loss. Such examples illustrate that the losses caused by FFE may be several times higher than the direct earthquake losses. FFE simulation can help improving regional building seismic loss estimation [Zeng et al., 2016]. As a result, adequate attention must be paid to FFE disasters.

Since the 1950s, different FFE models have been proposed and developed worldwide. Lee et al. [2008] presented a well-organized review of the FFE models being developed before 2008. The existing FFE models are mainly categorized into two types: (1) ignition models, which simulate the number of ignited buildings in a given zone under a certain seismic intensity, and (2) fire spread models, which simulate the fire development in an individual building and fire spread among neighborhood buildings. Most of the ignition models (e.g., all 15 ignition models mentioned in Lee et al. [2008]) use the regression methods to regress the ignition rate on seismic intensity measures (e.g., peak ground acceleration (PGA)), based on the statistics of historical FFE events. In contrast, fire spread models have a tendency towards being physics-based rather than strictly empirical [Lee et al., 2008].

After 2008, the FFE models underwent several new developments. With regard to the ignition models, Davidson [2009], Anderson et al. [2016] adopted new statistical models (e.g., Generalized Linear Models) with more variables instead of considering only PGA in the conventional regression models. Zolfaghari et al. [2009], Yildiz and Karaman [2013] established the event tree model, which defines the igniting probability of buildings according to the post-earthquake damage states of the electrical system, gas system, water pipelines, furniture and other contents inside the buildings. Thus, the event tree model is able to consider more detailed building characteristics compared to the regression models. The event tree model can also be used in fire hazard analysis for gas network damage [Omidvar and Kivi, 2016]. With respect to the fire spread models, Thomas et al. [2012], Cousins et al. [2012] developed the cellular automaton model and the static burn-zone model based on their previous research outcomes; and these new models were then applied to the FFE simulation of the 1995 Kobe earthquake and the FFE prediction of the Wellington area. Lee and Davidson [2010a] proposed a new physics-based fire spread model, which can recognize different fire spread forms (room-to-room spread and building-to-building spread) and different flame behaviors (roof flames and window flames), and their models were employed to the FFE simulation of Los Angeles [Lee and Davidson, 2010b] and the fire spread simulation of Grass Valley in California, 2007 [Li and Davidson, 2013]. Zhao [2010] proposed a FFE model based on a geographic information system (GIS) platform, following the FFE models of Himoto and Tanaka [2000, 2003]. Himoto and Tanaka also updated their previously proposed FFE models [Himoto and Tanaka, 2000, 2003] which resulted in a physics-based urban fire spread model [Himoto and Tanaka, 2008]. The physics-based urban fire spread model was further improved to simulate the FFE [Himoto et al., 2013], in which the influence of earthquake and fire-induced building damage on fire spread were well-considered.

Despite the aforementioned developments, some limitations of the existing FFE models can be identified as follows:

(1) The exact ignition locations are difficult to be obtained using the existing ignition models. Generally, the regression models only provide the number of ignited buildings, N, at a given seismic intensity. However, the exact ignition locations are determined randomly or arbitrarily assigned by users. Ren and Xie [2004] proposed an equation to calculate the building igniting probability, considering building damage states, and assumed that the top N buildings with the highest igniting probability are the ignited buildings, thus providing an approach to determine the ignition locations. However, how to calculate the damage states of a building group was not discussed in Ren and Xie [2004]¡¯s work.

(2) Only a limited number of fire spread models consider the influence of building seismic damage on fire spread. An earthquake may induce damage to walls, fire protection devices, gas systems, electrical systems, etc., which can further aggravate the fire spread. However, such effects are rarely considered in the existing fire spread models. The model of Himoto et al. [2013] made a remarkable progress with respect to these effects. Nevertheless, the seismic damage of buildings was randomly assigned in the case study of Himoto et al. [2013] and there were no further discussions as how to simulate the building seismic damage in urban regions.

(3) The high-fidelity visualization of conflagration in an urban region is rarely mentioned in the existing models. One of the important applications of FFE simulation is to support the decision making for fire protection planning and firefighting tasks. The decision makers in government departments or fire departments are generally non-professional people with limited knowledge of earthquake engineering. As a result, a high-fidelity visualization of conflagration is highly desirable for such non-professional users to better understand and interpret the fire scenario. The existing models usually display the fire spread results using a 2D GIS platform or a 3D platform, but few models covered the flame and smoke effects to enhance the reality of a fire spread scene, resulting in limited application among non-professionals.

Remarkable progress has been achieved in developing a novel seismic damage simulation method for regional buildings in recent years [Lu et al., 2014, Xiong et al., 2016a, b]. Using multiple degree-of-freedom (MDOF) models in conjunction with nonlinear time-history analysis (THA), the dynamic seismic responses of a number of buildings can be obtained in an efficient and accurate way, which has the potential to further improve the capacity of the FFE models. Specifically, the influence of building seismic damage on fire ignition and spread can be considered more reasonably. Therefore, in this work, a framework for the simulation and visualization of FFE, considering building seismic damage, is proposed based on the existing models of Lu et al. [2014] and Xiong et al. [2016a, b]. Specifically, the seismic damage of regional buildings is simulated using the MDOF building model and nonlinear THA. Moreover, a high-fidelity visualization of FFE is developed based on the OpenSceneGraph (OSG) 3D graphics engine and Fire Dynamic Simulator (FDS) software. A case study of the FFE simulation of downtown Taiyuan City with 44,152 buildings is performed. The results show that the influence of different ground motions and building seismic resistance on ignition locations and fire spread can be reliably considered in the proposed method and that the FFE scene can be displayed realistically. The proposed FFE simulation and visualization method can provide important technical support for FFE prevention and virtual reality-based fire disaster training.

2. Framework of FFE simulation and visualization

As shown in Figure 1, the proposed framework consists of four modules: (1) seismic damage simulation of regional buildings; (2) ignition model; (3) fire spread model; and (4) high-fidelity visualization of FFE. These modules are elaborated below.

Fig. 1 The proposed framework of FFE simulation and visualization.

Module 1, seismic damage simulation of regional buildings, forms the basis of FFE simulation. The authors¡¯ previous research outcomes on building seismic damage simulations based on the MDOF model and nonlinear THA [Lu et al., 2014, Xiong et al., 2016a, b] are adopted herein so that the features of individual buildings and different ground motions can be considered more reasonably.

Module 2, the ignition model, is developed based on the existing regression model and probabilistic model proposed by Ren and Xie [2004], so that the influence of building seismic damage can be considered more reasonably. In the proposed ignition model, more severe building damage leads to higher building igniting probability. Consequently, different earthquakes will affect the igniting probability distribution and ignition locations.

Module 3, the fire spread model, is developed based on the existing physics-based model proposed by Zhao [2010] to include the impact of building seismic damage on fire spread. Noting that earthquakes also induce damage on the building exterior façade, therefore in the proposed fire spread model, more severe damage of an exterior façade is considered to produce lower critical heat flux of ignition. Consequently, the fire spread characteristics among buildings will be affected by the features of different earthquakes.

Module 4, high-fidelity visualization, displays the fire spread process and smoke effects in a 3D platform. The 3D scene of regional buildings is established using OSG, an open-source 3D graphics engine [OSG, 2016]. Different burning states are represented by different color contours so that the changes of building burning states and fire spread can be clearly illustrated. The motions of smoke particles are calculated using FDS software [NIST, 2016] and displayed in Smokeview, which is the post-processing software of FDS [NIST, 2016], so that the smoke effects of conflagration can be visualized realistically.

The abovementioned four modules serve as the computing modules of the FFE simulation and visualization. The initial data required by the computing modules are stored and organized in a GIS platform; while during the runtime, the data are transferred among the four modules via intermediate files, as shown in Figure 2.

Fig. 2 Data exchanges among computing modules

There are generally two types of data stored in the GIS platform. One is building information, such as building geometry, number of stories, building height, structural type, construction year, building occupancy, etc. The other is related to the simulation settings, such as the ground motion input, weather conditions (ambient temperature, humidity, wind speed, wind direction, etc.), total simulation time, simulation time step, etc. Each module obtains the corresponding data from the GIS platform as input (Figure 2).

Several data exchanges are also required among the four modules. Module 1 (seismic damage simulation of regional buildings) generates building damage state files, which are used as input for Module 2 (ignition) and Module 3 (fire spread); Module 2 (ignition) generates the IDs of ignited buildings, required as the input for Module 3 (fire spread); Module 3 (fire spread) calculates the ignition time and burning duration of each ignited building, as the input for Module 4 (visualization); the final output are the fire spread scene and smoke effects.

3. Methodology

Detailed explanations of the underlying methodologies for each of the four modules are presented below.

3.1 Module 1, seismic damage simulation of regional buildings

Module 1, seismic damage simulation of regional buildings, forms the basis of the subsequent FFE simulation. There are thousands of buildings in an urban region. Establishing a computational model and calculating the seismic response of every single building will lead to an enormous workload, which is a great challenge. To obtain an accurate and efficient seismic damage simulation of regional buildings, Xiong et al. [2016a, b] performed a series of studies in which the low- and mid-rise buildings were simulated using the nonlinear MDOF shear models and the tall buildings were simulated using the nonlinear MDOF flexural-shear models. Meanwhile, based on the design process specified in the design codes [CMC, 2010] and sufficient experimental data, the corresponding parameter determination and damage assessment methods were also proposed [Xiong et al., 2016a, b], the inter-story backbone curves and hysteretic parameters of the MDOF models can be determined based on the basic building GIS information (i.e., planar area, number of stories, building height, construction period, occupation and structural type). As a result, the nonlinear MDOF model of buildings can be automatically established. After that, the nonlinear THA is performed to calculate the seismic responses and damage of the buildings. The nonlinear THA of a number of buildings can be greatly accelerated through graphics processing unit (GPU)-powered parallel computing [Lu et al., 2014, Xu et al., 2016b]. Xiong et al. [2016a, b] validated the rationality and accuracy of these methods via plenty of case studies.

3.2 Module 2, ignition model

Most of the existing ignition models regress the ignition rate according to the statistics of historical FFE events, however the exact locations of ignition are determined randomly or arbitrarily assigned by the users. To determine the ignition locations more reasonably, Ren and Xie [2004] proposed the following methodology: (1) calculate the number of ignited buildings N using the regression model, given a seismic intensity; (2) calculate the igniting probability of each building using the probabilistic model of individual buildings; (3) sort the buildings in the target region by building igniting probability in a descending order; and (4) assign the top N buildings with the highest igniting probability as the ignited buildings.

Since the regression models rely on the statistical data, a regression model generally performs better when applied to the regions where the historical FFE records are included in the statistics. As the case study presented in this work is a Chinese city, amongst the existing regression models, the model proposed by Ren and Xie [2004], which uses the statistical data of historical FFE events in China, the United States, and Japan during 1900-1996, is therefore adopted in this work, as shown in Eq. (1):

                                                          (1)

where N is the number of ignited buildings per 1 million m² building area. The unit of PGA is g.

Given a PGA, the igniting probability of an individual building  can be calculated using Eqs. (2) and (3) [Ren and Xie, 2004]:

                                                (2)

                                               (3)

where  represents the influence of building seismic damage on the igniting probability, given a PGA. The meanings and values of other parameters are listed in Table 1.

Table 1. Descriptions of the parameters in the equations of the probabilistic model

Note that the igniting probability given by Eq. (2) may overestimate the ignition risk (i.e., the expected number of ignited buildings predicted by Eq. (2) (the sum of the igniting probabilities of all the buildings) will be greater than the number of buildings given by Eq. (1)). As a result, the  proposed by Ren and Xie [2004] should be treated as a measurement of relative igniting risk of different buildings instead of an absolute igniting risk. In other words, a higher  indicates a higher FFE igniting risk of a building. To emphasize this point and to avoid misleading, a new index, i.e., the building ignition index r, is defined herein as:

                                                                                                (4)

where  is the maximum value of Eqs. (2) and (3), under the condition that the building collapses due to an earthquake, the building contains flammable and explosive chemical material, and the weather conditions are unfavorable [Ren and Xie, 2004].

Ren and Xie [2004] provided the values of most parameters listed in Table 1, but they did not mention how to calculate . Some studies suggested using damage probability matrices to calculate  [Zhao, 2006]. However, the damage probability matrices cannot identify the influence of different ground motion characteristics (e.g., with or without velocity pulse). Moreover, for the regions lacking historical seismic damage data, the accuracy of damage probability matrices should be carefully considered [Xiong et al., 2016b]. For this reason, the seismic damage simulation of regional buildings proposed by Xiong et al. [2016a, b] (Section 3.1) is used in this study to calculate the probability of buildings experiencing different damage states, as summarized in the following steps:

          (1)     Select n ground motions as input, given a PGA. The ground motion selection approach refers to the existing studies [FEMA, 2012]. Particularly, if the FFE of a certain earthquake scenario is considered, then n = 1, i.e., directly generate the ground motion based on the target earthquake scenario [Chaljub et al., 2010, Diao et al., 2016].

          (2)     Perform n times of nonlinear THA for a building. Each THA generates a certain damage state of the building (e.g., none, slight, moderate, extensive, or collapse), so as to obtain the frequency of occurrence n_j for each damage state D_j.

          (3)     Calculate  by solving Eq. (5):

                                                                                                       (5)

          (4)     Repeatedly perform Steps (1) - (3) for each building in the region. Using Eqs. (2) - (5), the distribution of building ignition index r in the region can be obtained. The top N buildings with the highest r are assigned as the ignited buildings.

Note that the influences of earthquake-induced building damage (e.g., damage of gas system and electrical system, overturning of furniture and appliances) on building igniting probability are rather complicated. Note also that Eqs. (2) and (3) only represent a simplified model in predicting the igniting probability. Although Zolfaghari et al. [2009], Yildiz and Karaman [2013] developed an event tree model for ignition that considers more detailed factors, such a model requires too much detailed indoor information of buildings that is hard to obtain for a regional simulation. As a result, this type of model is not adopted in this work.

3.3 Module 3, fire spread model

Fire spread consists of fire development in an individual building and fire spread among a group of buildings. The fire spread model proposed by Zhao [2010] is adopted in this work. In Zhao [2010]¡¯s model, the fire development in an individual building (i.e., ignition, flashover, full-development, and extinguishment) is simplified by defining the temperature and heat release rate of the burning building versus time. For the fire spread among a group of buildings, two main mechanisms that affect the fire spread, i.e., thermal radiation and thermal plume, are considered in Zhao [2010]¡¯s model (Figure 3). The burning buildings not only affect adjacent buildings via ejected flames and radiation through openings and heated exterior walls but also affect the buildings in the downwind direction via plumes with high temperature. For a building that has not caught fire, if the received heat flux from the burning buildings is higher than its critical heat flux, it will then be ignited. Moreover, the influence of weather conditions, e.g., ambient temperature, humidity and rain, are also considered in Zhao [2010]¡¯s fire spread model. The fire spread model was validated by comparing the simulation and real fire spread of the fire following the 1995 Kobe earthquake. Details of the validation can be found in Zhao [2010].

Fig. 3 Two main mechanisms affecting fire spread among buildings: thermal radiation and thermal plume

It is worthy to note that both the fire development in an individual building and the fire spread among a group of buildings are very complicated in reality. Although many fire development models for an individual building have been proposed [Sekizawa, 2003, Cheng and Hadjisophocleous, 2011], in which more detailed information (e.g., room layout, sprinklers, etc.) were taken into consideration, such models can hardly be used for regional FFE simulation because the detailed indoor information cannot be obtained for every building in an urban region. Amongst the available models, Zhao [2010]¡¯s model has been found to be mostly suitable for an urban region with a high density of low-rise buildings, which normally presents a higher FFE risk as confirmed by many past FFE events. Thus, although Zhao [2010]¡¯s model has some limitations, it is still one of the best options for FFE simulation.

It should be noted, however, that the building seismic damage is not considered in Zhao [2010]¡¯s model. As a matter of fact, seismic damage reduces the building fire resistance, hence aggravating fire spread. To date, only a limited number of existing fire spread models deals with building seismic damage, among which a representative model was proposed by Himoto et al. [2013]. In this model, the difference in the burning behavior between collapsed and non-collapsed buildings can be identified. Noting that earthquakes also induce failure of the building exterior façade for non-collapsed buildings. Consequently, a more severe façade failure expedites ignition of the buildings by the adjacent burning buildings.

The principle of the work of Himoto et al. [2013] is adopted in this work, i.e., assuming that the failure of the building exterior façade due to an earthquake will reduce the critical heat flux of ignition, as shown in Eq. (6).

                                                                                           (6)

where  is the failure ratio of the exterior façade, defined as the ratio of failed area to the total area of the exterior façade; ,  are the critical heat flux when  and , respectively. The value of   can be referred to Zhao [2010].

 is defined as the critical heat flux reduction factor when the complete failure of the exterior façade occurs, as shown in Eq. (7).

                                                                                                                    (7)

However, the value of  lacks sufficient references; hence, the influence of  on the fire spread simulation results will be further discussed in the case study of this work.

The failure ratio of the exterior façade  is correlated to the building seismic damage states. Based on the seismic damage investigation data of the 1995 Kobe earthquake, Hayashi et al. [2005] proposed a relationship between  and the building seismic damage states. Due to the lack of other data sources, the work of Hayashi et al. [2005] is thus adopted herein.

Note that Himoto et al. [2013] did not provide further discussions on how to determine the building seismic damage; instead, the damage states of buildings were randomly assigned in their work. To overcome this limitation, Section 3.1 in this work provides a more reasonable prediction of building seismic damage simulation.

3.4 Module 4, high-fidelity visualization

Decision makers in government departments or fire departments are generally non-professional people with limited knowledge of earthquake engineering. As a result, it is necessary to provide a realistic scene of conflagration based on the simulation results. Two components of a high-fidelity visualization for FFE are presented in this section:

Component 1: Fire spread. The development of building burning states and fire spread in the entire region can be clearly shown by changing the color contours of the buildings. Such outcomes can assist the decision makers to better understand the overall situation of the fire spread area and direction, estimate the sub-regions with high risks of FFE, and make decisions regarding fire rescue and fire protection planning.

Component 2: Smoke effects. Using particle systems, the smoke diffusion of a fire scene can be displayed in a 3D platform. The smoke effects can enhance the reality of the fire scene and provide a high-fidelity virtual reality scene for practical applications such as fire disaster training [Xu et al. 2014a].

The fire spread visualization component is based on the work of Xu et al. [2014b], using the open-source 3D graphics engine, OSG. The flowchart of the fire spread visualization component is shown in Figure 4. Specifically, by extruding the 2D building polygons based on the building information (i.e., the number of stories, building height, and planar shape), the 3D models are created as OSG Geodes (geometry nodes) and added to the root node of the fire scene. The burning states of buildings at every minute are determined according to the simulation results of fire ignition and spread. Different burning states are identified using different color contours. A node callback class is defined, which is called for each frame during the OSG fire scene rendering to update the building color contours frame-by-frame. The technology of adding building textures, proposed by Xu et al. [2014b], is substituted by adding color contours to represent the building burning states.

Fig. 4 Flowchart of the high-fidelity visualization

To add a realistic smoke effect to the fire scene, FDS software is used to perform the computational fluid dynamics analysis for the fire development in a large-scale open region. The motions of smoke particles can be directly computed by FDS using the large-eddy simulation (LES), which follows the laws of physics and generates a realistic smoke diffusion. By contrast, the particle system in OSG cannot generate such a realistic smoke effect. The flowchart of the smoke effect visualization component is shown in Figure 4. The PyroSim software [Thunderhead, 2016] is used to convert the 3D OSG building models into FDS geometry models. Specifically, the 3D building models are exported using the osgDB::writeNodeFile() method provided by OSG and then imported into PyroSim. Subsequently, PyroSim outputs the geometry information, following the input file format of FDS. The ignition time and burning duration of each ignited building (defined respectively by the ¡°&DEVC¡± and ¡°&SURF¡± keywords in FDS) are obtained and added to the FDS model file according to the simulation results of fire ignition and spread. Other simulation settings, such as wind and simulation time, are also added to the FDS model file. Then, the FDS model file is submitted as a computational job and the simulation results are visualized in Smokeview, which is the post-process software of FDS.

According to the above descriptions of the four modules, the proposed framework of fire following earthquake (FFE) simulation and visualization can be feasibly implemented. In addition, both the FDS and Smokeview are open-source and cross-platform software, which are easily accessible through the Internet. The case study presented in Section 4 shows that the proposed method and software can be applied for large cities with tens of thousands of buildings. Hence the method developed in this study and the associated software are well suited for FFE simulation and visualization for most urban areas.

4. Case study: downtown Taiyuan City

4.1 Introduction of the case study region

Downtown Taiyuan City in China, consisting of 44,152 buildings, has a gross area of approximately 26 km², as shown in Figure 5. The statistics of the number of buildings with different stories are presented in Figure 6, indicating that most buildings are low-rise buildings. Thus, Zhao [2010]¡¯s model is suitable for this region.

Fig. 5 Case study region, downtown Taiyuan City, China: a The region (Source: Google maps), b 3D sketch

Fig. 6 Statistics of the number of buildings with different stories in downtown Taiyuan City

According to the Chinese Code for Seismic Design of Buildings [CMC, 2010], the buildings in downtown Taiyuan City have a seismic design intensity of VIII, i.e., the PGA is 0.2 g for a Design Basis Earthquake (DBE) with a return period of 475 years. Based on the design spectrum defined in CMC [2010] as the target spectrum, 30 ground motions are selected and scaled from the PEER NGA-West2 database as the input ground motions using the online tools provided by the Pacific Earthquake Engineering Research Center [PEER, 2016]. As shown in Figure 7, the spectra of input ground motions match well with the target spectrum at the period range of low- and mid-rise buildings (i.e., with fundamental periods less than 2 s).

Fig. 7 Response spectra of the input ground motions and the target spectrum

The DBE hazard level (PGA = 0.2 g) is selected in this case study. At the DBE hazard level, the damage states of many old, non-engineered buildings are indicated as either collapse or extensive, while the damage states of newly built, engineered buildings are shown to be moderate or lower. In consequence, such a hazard level clearly demonstrates that the proposed method is able to consider the influence of different building damage states on FFE. If the seismic intensity is too high (or too low), the damage states may show to be extensive (or slight) for most buildings; and for such cases, the advantages of the proposed method may not be illustrated clearly.

4.2 Ignition simulation

The damage states of buildings can be obtained by performing the nonlinear THA for all the buildings in the case study region, using the 30 ground motions shown in Figure 7 as input. Subsequently, the ignition indices r under different ground motions and the mean ignition indices r_m can be calculated using Eqs. (2) - (5). When PGA = 0.2 g, the number of ignited buildings is found to be N = 32, according to Eq. (1). The top N buildings with the highest r_m are assumed to be the ignited buildings, as shown in Figure 8. The ignition indices are sorted in a descending order; and the orders are marked by the circled numbers in Figure 8 (a smaller number means a higher ignition index). Furthermore, the top 1000 buildings that are most severely damaged are identified in Figure 9. This case study confirms a strong correlation between the building seismic damage and the igniting probability, which is considered rational theoretically.

Fig. 8 The mean ignition index of each building and the locations of the 32 ignited buildings

Fig. 9 The locations of top 1000 most severely damaged buildings

The distributions of building ignition indices and igniting locations are different when subjected to different ground motions due to the variability of ground motions. To further illustrate such a difference, two ground motions are selected from the 30 ground motion records. One is a near-field ground motion record (Imperial Valley-02, El Centro Array #9), while the other is a far-field record (Northwest Calif-02, Ferndale City Hall). Figure 10 shows the ignition simulation results of the two ground motions. Note that different ground motions have different spectra even though their PGAs are identical, resulting in different damage to buildings with different dynamic characteristics. In consequence, the distributions of fire spread are different under different ground motions. By contrast, if the building damage is calculated using damage probability matrices, the ignition distribution results will be identical at the same PGA value.

Fig. 10 The building ignition indices under the two selected ground motions

4.3 Fire spread simulation

Weather conditions of west wind (wind speed v = 6 m/s), the lowest ambient temperature T_low = 10 ¡ãC, the highest ambient temperature T_high = 25 ¡ãC, and the critical heat flux reduction factor  are selected as an example. The fire spread simulation is performed after obtaining the ignition location. The mean and standard deviation of the total footprint area burned subsequent to different ground motions are shown in Figure 11. The fire spread is found to speed up at the beginning of the conflagration and slow down after 18 h. However, for some ground motions, speed-up occurs again during 20 h-35 h. After 45 h, the fire is extinguished completely. When the suppression by the fire departments is not considered, the mean total footprint area burned is approximately 0.45 km², accounting for 5.5% of the total footprint area of the buildings. After approximately 6 h, the differences of fire spread results under different ground motions start to increase. At 45 h, the coefficient of variation (the ratio of standard deviation to mean) of the total footprint area burned is approximately 5% due to different ground motions.

Fig. 11 Total footprint area burned vs. time: the mean and standard deviation

Due to the lack of sufficient data with respect to the value of critical heat flux reduction factor , the influence of this factor on the fire spread is discussed herein. When the weather conditions and ignition locations remain the same, the total footprint area burned (mean of the results of 30 ground motions) versus time for different values of  are as shown in Figure 12. After 45 h, the fire is extinguished completely. Note that  indicates that the influence of building seismic damage on fire spread is not considered. Figure 12 shows that given the same seismic damage of buildings, a smaller , i.e., a lower critical heat flux when the exterior façade completely fails, results in a larger area burned, i.e., a greater aggravation of the fire spread due to the building damage. When , the total area burned (at 45 h), considering building damage, increases by 10%, compared to not considering building damage.

Fig. 12 Total footprint area burned vs. time for different values of .

Wind is an important factor affecting fire spread. When other conditions remain the same (when ), the total footprint area burned (mean of the results of 30 ground motions) versus time for different wind speeds v are shown in Figure 13. When v = 2 m/s, the spread speed and the total burned areas are almost the same with v = 0 m/s. When the wind speed is further increased, both the fire spread speed and the total burned area increase. When v = 6 m/s, the total burned area increases by 42% compared to v = 0 m/s. Hence, the wind speed has a significant influence on fire spread. According to the yearbook of Taiyuan city [Taiyuan, 2015], the annual average wind speed of Taiyuan is 1.4~2.2 m/s. Given this range of wind speed, the expected total footprint area burned is approximately 0.31 km², accounting for 3.8% of the total footprint area of the buildings. Moreover, the expected fire duration is approximately 22 h. It should be noted, however, that if the wind speed reaches 6 m/s, the burned area will dramatically increase (Figure 13). Hence if the wind speed happens to be far beyond the average (1.4~2.2 m/s), the FFE disaster may be much more severe than expected.

Fig. 13 Total footprint area burned vs. time for different wind speeds. v stands for wind speed (unit: m/s)

The case study results indicate that the proposed fire spread model is able to evaluate the influences of different ground motions on fire spread and hence identify the characteristics and variability of the ground motions. Moreover, the proposed model takes into consideration the influence of wind speed reasonably.

4.4 High-fidelity visualization results

The visualization of fire spread is demonstrated in Figure 14. Figures 14 (a) to (c) show the fire spread situation at 4 h, 6 h, and 10 h, respectively. The development of fire is clearly displayed using different color contours. The smoke effect is presented in Figure 15. It is evident that the motions of the smoke particles can enhance the reality of the fire scene, from which the fire location and damage severity of the urban region can be clearly identified.

Fig. 14 Fire spread effects using OSG: a t = 4 h, b t = 6 h, c t = 10 h

It should be noted that the proposed method involves certain assumptions, including: (1) The parameters of the structural analysis models are determined based on the experimental data of regular buildings. As for special buildings whose dynamic properties are significantly different from those of the regular buildings, their seismic behaviors require special considerations. (2) The regression model employed in the ignition module is based on the statistical data of FFE events in China, the United States, and Japan, hence is most suitable for urban regions in these countries. With respect to other regions, different regression models are required to be developed. (3) Fire sprinkler and suppression systems as well as the fire department are not considered in the fire spread model. Nonetheless, it should be noted that an earthquake may cause damage to the sprinkler systems, and the fire department may not respond quickly enough. Hence the proposed method, being able to produce conservative simulation results, is considered a rational approach. (4) The openings (doors and windows) are not displayed in the 3D building models. Nevertheless, using such a level of detail in this work is sufficient for creating a realistic fire scene, as shown in the case study (Figure 15).

Fig. 15 Smoke effects displayed in Smokeview: a global view, b local view

5. Conclusions

In this work, a framework for physics-based simulation and high-fidelity visualization of FFE, considering the building seismic damage, are proposed. A case study of the FFE simulation of downtown Taiyuan City is performed. The conclusions can be drawn as follows:

          (1)     The seismic damage of regional buildings is simulated using the nonlinear MDOF building model and nonlinear THA, which is necessary for FFE simulation. Consequently, the influence of different ground motions and different building seismic resistances on the fire ignition locations and fire spread can be considered, which leads to a more rational and accurate FFE simulation.

          (2)     The fire spread outcomes of different ground motions are similar to each other in the initial stage of FFE; however they deviate with time. The seismic damage to an exterior façade will induce a larger burned area.

          (3)     Based on the OSG graphics engine, the dynamic process of fire development can be clearly displayed using different color contours; using FDS and Smokeview, the smoke effects can be visualized realistically. Such results will facilitate non-professional users in their efforts in preventing and mitigating the FFE.

Acknowledgements

Professor Kincho Law in Stanford University gave constructive suggestions on this paper. The authors are grateful for the financial support received from the National Natural Science Foundation of China (No. 51578320), and the China Scholarship Council. The authors are also grateful for the Thunderhead Engineering Consultants, Inc. for providing the PyroSim software for free.

References

Anderson, D., Davidson, R. A., Himoto, K. and Scawthorn, C. [2016] "Statistical modeling of fire occurrence using data from the thoku, japan earthquake and tsunami," Risk Analysis 36(2), 378-395.

Chaljub, E., Moczo, P., Tsuno, S., Bard, P. Y., Kristek, J., Käser, M., Stupazzini, M. and Kristekova, M. [2010] "Quantitative comparison of four numerical predictions of 3D ground motion in the grenoble valley, france," Bulletin of the Seismological Society of America 100(4), 1427-1455.

Cheng, H. and Hadjisophocleous, G. V. [2011] "Dynamic modeling of fire spread in building," Fire Safety Journal 46(4), 211-224.

China Ministry of Construction (CMC) [2010] Code for seismic design of buildings, GB50011-2010. China Architecture and Building Press, Beijing (in Chinese)

Cousins, J., Thomas, G., Heron, D. and Smith, W. [2012] "Probabilistic modeling of post-earthquake fire in wellington, new zealand," Earthquake Spectra 28(2), 553-571.

Davidson, R. A. [2009] "Modeling postearthquake fire ignitions using generalized linear (mixed) models," Journal of Infrastructure Systems 15(4), 351-360.

Diao, F., Wang, R., Aochi, H., Walter, T. R., Zhang, Y., Zheng, Y. and Xiong, X. [2016] "Rapid kinematic finite-fault inversion for an mw 7+ scenario earthquake in the marmara sea: an uncertainty study," Geophysical Journal International 204(2), 813-824.

Federal Emergency Management Agency (FEMA) [2012] Seismic performance assessment of buildings volume 1 - methodology, Technical report FEMA P-58, Washington, DC.

Hayashi, Y., Inoue, M., Kuo, K. C. and Suita, K. [2005] "Damage ratio functions of steel buildings in 1995 hyogo-ken nanbu earthquake," Proc. of ICOSSAR 2005, Rotterdam, Nederland, pp. 633-639.

Himoto, K. and Tanaka, T. [2000] "A preliminary model for urban fire spread-building fire behavior under the influence of external heat and wind", Thirteenth meeting of the UJNR panel on fire research and safety, pp. 309-319.

Himoto, K. and Tanaka, T. [2003] "A physically-based model for urban fire spread," Fire Safety Science 7129-140.

Himoto, K. and Tanaka, T. [2008] "Development and validation of a physics-based urban fire spread model," Fire Safety Journal 43(7), 477-494.

Himoto, K., Mukaibo, K., Akimoto, Y., Kuroda, R., Hokugo, A. and Tanaka, T. [2013] "A physics-based model for post-earthquake fire spread considering damage to building components caused by seismic motion and heating by fire," Earthquake Spectra 29(3), 793-816.

Lee, S. W. and Davidson, R. A. [2010a] "Application of a physics-based simulation model to examine post-earthquake fire spread," Journal of Earthquake Engineering 14(5), 688-705.

Lee, S. W. and Davidson, R. A. [2010b] "Physics-based simulation model of post-earthquake fire spread," Journal of Earthquake Engineering 14(5), 670-687.

Lee, S., Davidson, R., Ohnishi, N. and Scawthorn, C. [2008] "Fire following earthquake¡ªreviewing the state-of-the-art of modeling," Earthquake Spectra 24(4), 933-967.

Li, S. and Davidson, R. [2013] "Application of an urban fire simulation model," Earthquake Spectra 29(4), 1369-1389.

Lu, X. Z., Han, B., Hori, M., Xiong, C. and Xu, Z. [2014] "A coarse-grained parallel approach for seismic damage simulations of urban areas based on refined models and GPU/CPU cooperative computing," Advances in Engineering Software 70, 90-103.

Mousavi, S., Bagchi, A. and Kodur, V. K. [2008] "Review of post-earthquake fire hazard to building structures," Canadian Journal of Civil Engineering 35(7), 689-698.

National Institute of Standards and Technology (NIST) [2016] Fire Dynamics Simulator (FDS) and Smokeview (SMV). https://pages.nist.gov/fds-smv/.

Omidvar, B. and Kivi, H. K. [2016] "Multi-hazard failure probability analysis of gas pipelines for earthquake shaking, ground failure and fire following earthquake," Natural Hazards 82(1), 703-720.

OpenSceneGraph (OSG) [2016] Openscenegraph Website. http://www.openscenegraph.org/

Pacific Earthquake Engineering Research Center (PEER) [2016] PEER ground motion database. http://ngawest2.berkeley.edu/

Ren, A. Z. and Xie, X. Y. [2004] "The simulation of post-earthquake fire-prone area based on GIS," Journal of Fire Sciences 22(5), 421-439.

Sathiparan, N. [2015] "Mesh type seismic retrofitting for masonry structures: critical issues and possible strategies," European Journal of Environmental and Civil Engineering 19(9), 1136-1154.

Scawthorn, C., Eidinger, J. and Schiff, A. [2005] "Fire following earthquake,¡± Technical Council on Lifeline Earthquake Engineering Monograph No. 26, American Society of Civil Engineers, Reston, VA.

Sekizawa, A. [2003] "Development of seismic-induced fire risk assessment method for a building.," Fire Safety Science 7309-320.

Taiyuan [2015] Taiyuan yearbook 2015, Taiyuan, Shanxi, China.

Thomas, G., Heron, D., Cousins, J. and de R¨®iste, M. [2012] "Modeling and estimating post-earthquake fire spread," Earthquake Spectra 28(2), 795-810.

Thunderhead [2016] Pyrosim: fire dynamics and smoke control, http://www.thunderheadeng.com/pyrosim/.

Xiong, C., Lu, X. Z., Guan, H. and Xu, Z. [2016a] "A nonlinear computational model for regional seismic simulation of tall buildings," Bulletin of Earthquake Engineering 14(4), 1047-1069.

Xiong, C., Lu, X. Z. and Lin, X. C. [2016b] "Parameter determination and damage assessment for tha-based regional seismic damage prediction of multi-story buildings," Journal of Earthquake Engineering, doi: 10.1080/13632469.2016.1160009

Xu, Z., Lu, X. Z., Guan, H., Chen, C. and Ren, A. Z. [2014a] "A virtual reality based fire training simulator with smoke hazard assessment capacity," Advances in Engineering Software 68(2), 1-8.

Xu, Z., Lu, X. Z., Guan, H., Han, B. and Ren, A. Z. [2014b] "Seismic damage simulation in urban areas based on a high-fidelity structural model and a physics engine," Natural Hazards 71(3), 1679-1693.

Xu, Z., Lu, X. Z., Guan, H., Tian, Y. and Ren, A. Z. [2016a] "Simulation of earthquake-induced hazards of falling exterior non-structural components and its application to emergency shelter design," Natural Hazards 80(2), 935-950.

Xu, Z., Lu, X. Z. and Law, K. H. [2016b] "A computational framework for regional seismic simulation of buildings with multiple fidelity models," Advances in Engineering Software 99, 100-110.

Yildiz, S. S. and Karaman, H. [2013] "Post-earthquake ignition vulnerability assessment of k¨¹ç¨¹kçekmece district," Natural Hazards and Earth System Sciences Discussions 1(3), 2005-2040.

Zeng, X., Lu, X. Z., Yang, T. Y. and Xu, Z. [2016] "Application of the FEMA-P58 methodology for regional earthquake loss prediction," Natural Hazards 83(1), 177-192.

Zhao, S. J. [2006] "Study on risk assessment and simulation of urban post-earthquake fire based on GIS, " Ph.D. thesis, Dept. of Civil Engineering, Tsinghua University, Beijing. (in Chinese)

Zhao, S. J. [2010] "GisFFE¡ªan integrated software system for the dynamic simulation of fires following an earthquake based on GIS," Fire Safety Journal 45(2), 83-97.

Zolfaghari, M. R., Peyghaleh, E. and Nasirzadeh, G. [2009] "Fire following earthquake, intra-structure ignition modeling," Journal of Fire Sciences 27(1), 45-79.

Table 1. Descriptions of the parameters in the equations of the probabilistic model.

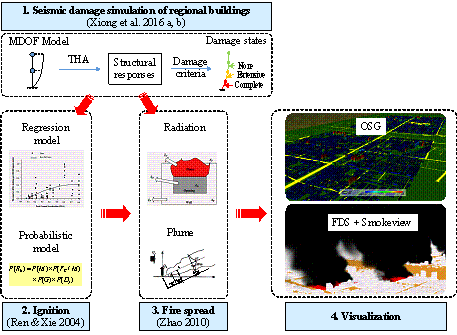
Figure 1. The proposed framework of FFE simulation and visualization.

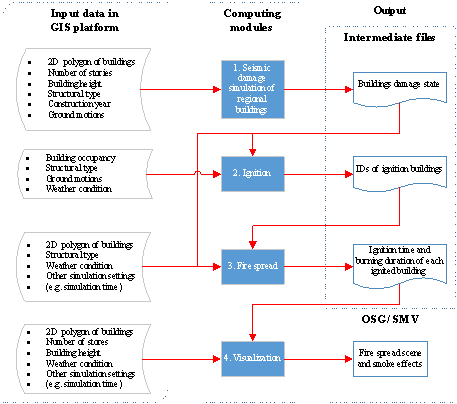
Figure 2. Data exchanges among computing modules.

Figure 3. Two main mechanisms affecting fire spread among buildings: thermal radiation and thermal plume.

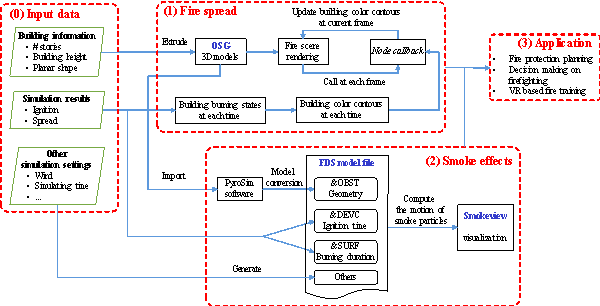
Figure 4. Flowchart of the high-fidelity visualization.

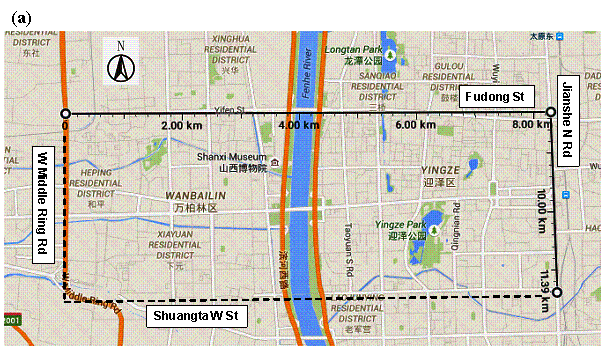
Figure 5. Case study region, downtown Taiyuan City, China: (a) The region (Source: Google maps), (b) 3D sketch.

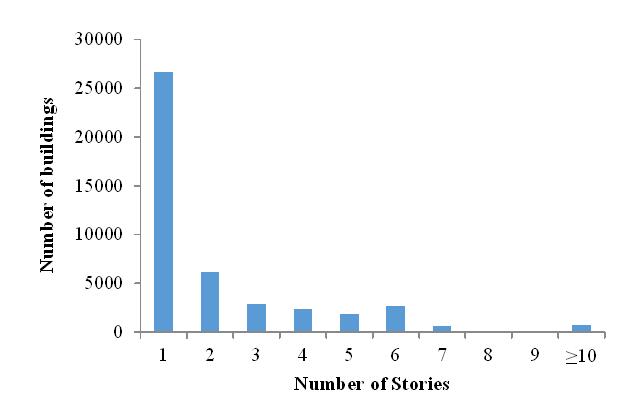
Figure 6. Statistics of the number of buildings with different stories in downtown Taiyuan City.

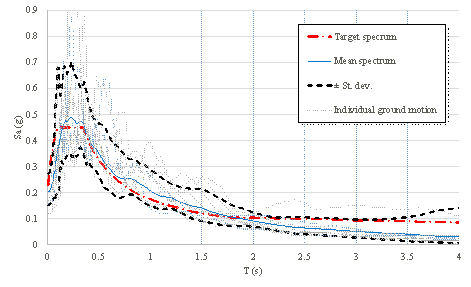
Figure 7. Response spectra of the input ground motions and the target spectrum.

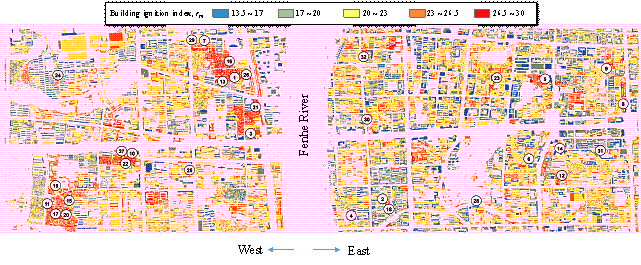
Figure 8. The mean ignition index of each building and the locations of the 32 ignited buildings.

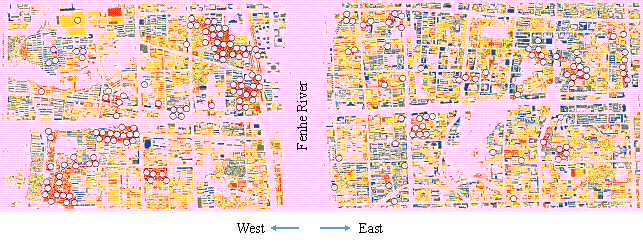
Figure 9. The locations of top 1000 most severely damaged buildings.

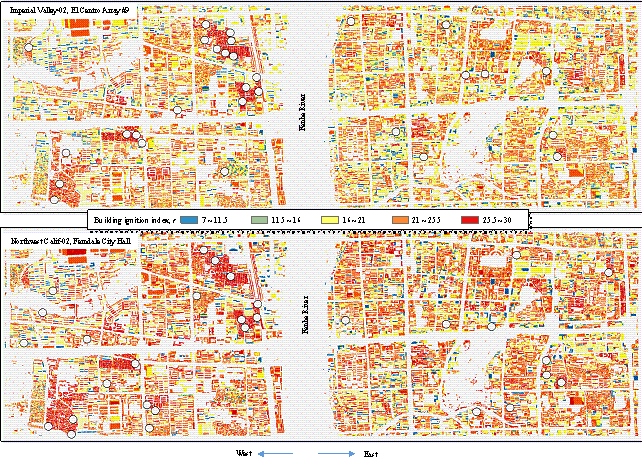
Figure 10. The building ignition indices under the two selected ground motions.

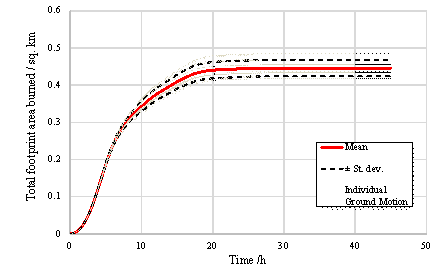
Figure 11. Total footprint area burned vs. time: the mean and standard deviation.

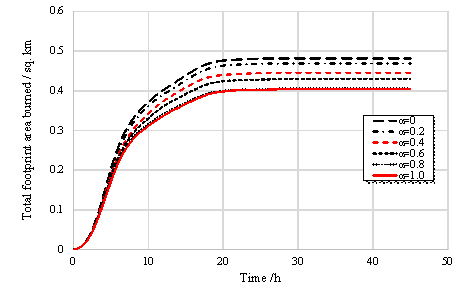
Figure 12. Total footprint area burned vs. time for different values of .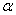

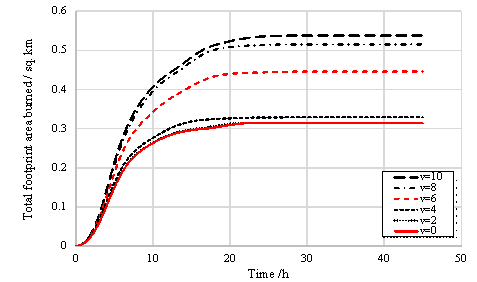
Figure 13. Total footprint area burned vs. time for different wind speeds. v stands for wind speed (unit: m/s).

Figure 14. Fire spread effects using OSG: (a) t = 4 h, (b) t = 6 h, (c) t = 10 h.

Figure 15. Smoke effects displayed in Smokeview: (a) global view, (b) local view.