|
5.
Conclusions
Worldwide competitions have rapidly increased
in the design and construction of super-tall buildings. The collapse resistance
study of these buildings has become a research frontier in earthquake engineering.
By using the fiber-beam elements, multi-layer shell elements and element-deactivation
technology, the earthquake-induced collapse simulation of an actual super-tall
mega-braced frame-core tube building (H = 550 m) to be built in China
is successfully conducted in this work. Both the El-Centro and KOBE ground
motions are selected and scaled up as input to induce collapse of the building.
The overall and detailed collapse processes, the critical collapse regions
and the corresponding structural responses are reported in some detail. The
simulation reveals that the main collapse mode of this super-tall building
is of vertical ¡°pancake¡± type. Furthermore, the actual collapse regions do
not necessarily coincide with the initial plastic zones predicted by the traditional
nonlinear time-history analysis. Therefore, the collapse simulation and analysis
are highly important to help identify the actual critical areas of the structures.
This study has provided a feasible methodology for the collapse simulation
of super-tall buildings of similar type. It can also serve as a reference
for the collapse-resistance design of this type of buildings.
Acknowledgment
The authors are grateful for the financial
support received from the National Nature Science Foundation of China (No.
51222804, 51261120377), the Tsinghua University Initiative Scientific Research
Program (No. 2010THZ02-1, 2011THZ03) and the Fok Ying Dong Education Foundation
(No. 131071).
References
[1]
"CTBUH Height Criteria". Council on Tall
Buildings and Urban Habitat. http://www.ctbuh.org/HighRiseInfo/TallestDatabase/Criteria/tabid/446/language/en-US/Default.aspx.
Retrieved 7 December 2011.
[2] L.
Xu, W.X. Shi, J. Zhang, Simulated earthquake experiment study of a high-rise
building structure model, J. Build. Struct. 22/5 (2001) 15-19. (in Chinese)
[3] C.S.
Li, S.S.E. Lam, M.Z. Zhang, Y.L. Wong, Shaking table test of a 1:20 scale
high-rise building with a transfer plate system, ASCE J. Struct. Eng. 132/11
(2006) 1732-1744.
[4] X.L.
Lu, Y. Zou, W.S. Lu, B. Zhao, Shaking table model test on Shanghai world financial
center tower, Earthq. Eng. Struct. Dyn. 36/4 (2007) 439-457.
[5]
Y.J. Mao, X.L. Lu, W.S. Lu, L.P. Kang, Shaking table model
test on Shanghai tower, J. Civ., Archit. Environ. Eng. 32/Sup.2 (2010) 534-536+549.
(in Chinese)
[6]
Z.Z. Zhao, H.J. Dong, J.R. Qian, Shaking table test and numerical analysis
on structural model of Beijing new poly plaza, In: Proceedings of 14th
World Conference on Earthquake Engineering, Beijing, China, 2008,
CDROM.
[7] C.L.
Wu, W.W. Kuo, Y.S. Yang, S.J. Hwang, C.H. Loh, Dynamic collapse simulation
of 3-bay RC frame under extreme earthquake loadings, In: ASCE Conference Proceedings,
Long Beach, California, USA 249/13 (2007) 1-14. doi:http://dx.doi.org/10.1061/40944(249)13.
[8] K. Toshikazu,
K. Toshimi, M. Taizo, K. Toshinori, K. Yousok, 3-D collapse tests and analyses
of the three-story reinforced concrete buildings with flexible foundation,
In: ASCE Conference Proceedings, Long Beach, California, USA 249/15
(2007) 1-14. doi:http://dx.doi.org/10.1061/40944(249)15.
[9]
S. Yamada, K. Suita, M. Tada, K. Kasai, Y. Matsuoka,
E. Sato, Collapse experiment on 4-story steel moment frame: Part 1,
In: Proceedings of 14th World Conference on Earthquake Engineering,
Beijing, China, 2008, CDROM.
[10] K.
Suita, S. Yamada, M. Tada, K. Kasai, Y. Matsuoka, E. Sato, Collapse experiment
on 4-story steel moment frame: Part 2, In: Proceedings
of 14th World Conference on Earthquake Engineering, Beijing, China,
2008, CDROM.
[11] W.J.
Yi, Q.F. He, Y. Xiao, Sashi K. Kunnath. Experimental study on progressive
collapse-resistant behavior of reinforced concrete frame structures, ACI Struct.
J. 105/4 (2008) 433-439.
[12] X.Z.
Lu, J.J. Jiang, Simulation for the collapse of WTC after aeroplane impact,
In: Proceedings of International Conference on Protection of Structures Against
Hazard, Singapore, 2002, pp. 57-60.
[13] X.
Quan, N.K. Birnbaum, Computer simulation of impact and collapse of New York
world trade center north tower on September 11, In: Proceedings of 20th
International Symposium on Ballistics, Orlando, Florida, USA, 2002, pp. 721-728.
[14] B.M.
Luccioni, R.D. Ambrosini, R.F. Danesi,
Analysis of building collapse under blast loads, Eng. Struct.
26 (2004) 63-71.
[15]
W. Huang, P. L. Gould, 3-D pushover analysis of a collapsed
reinforced concrete chimney, Finite. Elem. Anal. Des. 43 (2007) 879-887
[16] H.
Fan, Q.S. Li, Y.T. Alex, L. Xu, Seismic analysis of the world¡¯s tallest building,
J. Constr. Steel Res. 65/5 (2009) 1206-1215.
[17] GB
5009-2001, Load code for the design of building structures,
Beijing: Ministry of Construction of the People's Republic of China, 2006.
(in Chinese)
[18] GB50011-2010,
Code for seismic design of buildings, Beijing: Ministry
of Housing and Urban-Rural Development of the People's Republic of China,
2010. (in Chinese)
[19] MSC.Software
Corp. MSC.Marc Volume A: Theory and User Information, 2007.
[20]
X. Lu, X.Z. Lu, H. Guan, L.P. Ye, Collapse simulation of reinforced
concrete high-rise building induced by extreme earthquakes, Earthquake Eng
Struct Dyn. (2012) DOI: 10.1002/eqe.2240.
[21]
Z.W. Miao, L.P. Ye, H. Guan, X.Z. Lu, Evaluation of modal and traditional pushover analyses
in frame-shear-wall structures,
Adv. Struct. Eng. 14/5 (2011) 815-836.
[22] L.H.
Han, X.L. Zhao, Z. Tao,
Tests and mechanics model of concrete-filled
SHS stub columns, columns
and beam-columns, Steel Compos. Struct. 1/1 (2001) 51¨C74.
[23]
L.H. Han, G.H. Yao, X.L. Zhao, Tests
and calculations for hollow structural steel (HSS) stub columns
filled with self-consolidating concrete (SCC), J. Constr. Steel Res. 61/9 (2005) 1241-1269.
[24]
L.H. Han, Concrete-filled steel tubular structures: theory
and practice, second ed., Science Press, Beijing, 2007. [in
Chinese]
[25] E. Spacone,
F. Filippou, F. Taucer, Fiber beam-column modeling for non-linear analysis
of R/C frames, Earthq. Eng. Struct. Dyn. 25/7 (1996) 711-725.
[26] B.X.
Tang, X.Z. Lu, L.P. Ye, W. Shi, Evaluation of collapse resistance of RC frame
structures for Chinese schools in seismic design categories B and C, Earthq.
Eng. Eng. Vib. 10/3 (2011) 369-377.
[27]
Y.
Li, X.Z. Lu, H. Guan, L.P. Ye, An improved tie force method for progressive
collapse resistance design of reinforced concrete frame structures, Eng. Struct.
33/10 (2011) 2931-2942.
[28] X.Z.
Lu, L.P. Ye, Y.H. Ma, D.Y. Tang, Lessons from the collapse of typical RC frames
in Xuankou School during the great Wenchuan Earthquake, Adv. Struct. Eng.
15/1 (2012) 167-181.
[29] GB
50017, Code for design of steel structures, Beijing: Ministry of Construction
of the People's Republic of China, 2006. (in Chinese)
[30] J.F.
Hajjar, B.C. Gourley, Representation of concrete-filled steel tube cross-section
strength, ASCE J. Struct. Eng. 122/11 (1996) 1327-1336.
[31] W.Z.
Zhang, M.S. Bahram, Comparison between ACI and AISC for concrete-filled tubular
columns, ASCE J. Struct. Eng. 125/11 (1999) 1213-23.
[32] A.H.
Varma, J.M. Ricles, R. Sause, Seismic behavior and modeling of high-strength
composite concrete-filled steel tube (CFT) beam-columns, J. Constr. Steel
Res. 58/5-8 (2002) 725-758.
[33] S.B.B.
Aval, M.A. Saadeghvaziri, A.A. Golafshani, Comprehensive Composite inelastic fiber element for cyclic analysis
of concrete-filled steel tube columns, ASCE J. Eng. Mech. 128/4 (2002) 428-437.
[34] P.
Tiziano, L. Roberto, Behavior of composite CFT beam-columns based on nonlinear
fiber element analysis, In: Proceedings of 2008 Composite Construction in
Steel and Concrete Conference VI, Devil's Thumb Ranch, Tabernash, Colorado,
USA, 2008, pp. 237-251.
[35] A.
Elremaily, A. Azizinamini, Behaviour and strength of circular
concrete-filled tube columns, J. Constr. Steel Res.,
58/ (2002)1567-1591.
[36] F.
Iannone, L. Mastrandrea, R. Montuori, V. Piluso, G. Rizzano, Prediction of
the ultimate behaviour of SHS-CFT members: experimental validation of a numerical
model, EUROSTEEL 2011, 6th European Conference on Steel and Composite Structures,
Budapest, September 2011, Vol. C, ISBN: 9789291471034, (2011) 2463- 2468.
[37] B.
Uy, Local and post-local buckling of concrete filled
steel welded box columns, J. Constr. Steel Res., 47/1-2, (1998) 47-72.
[38] K.C.
Tsai, P.C. Hsiao, K.J. Wang, Y.T. Weng, M.L. Lin, K.C. Lin, C.H. Chen, J.W.
Lai, S.L. Lin, Pseudo-dynamic tests of a full-scale CFT/BRB frame¡ªPart I:Specimen
design, experiment and analysis, Earthquake Eng. Struct. Dyn., 37/7, (2008)
1081-1098.
[39] J.
Wang, W.D. Wang, P.P. Zhang, Dynamic time history analyses of concrete-filled
steel tubular frames based on nonlinear fiber beam-column element, Earthquake
Resistant Engineering and Retrofitting, 33/2, (2011) 9-15. (in Chinese)
[40] X.Z.
Lu, X.C. Lin, Y.H. Ma, Y. Li, L.P. Ye, Numerical
simulation for the progressive collapse of concrete building due to earthquake,
In: Proceedings of 14th World Conference on Earthquake Engineering,
Beijing, China, 2008, CDROM.
[41]
GB50010-2010£¬
Code for design of concrete structures, Beijing: Ministry of Housing and Urban-Rural
Development of the People's Republic of China, 2010. (in Chinese)
[42]
Pacific Earthquake Engineering Research Center, PEER strong
motion database, California, Berkley, From URL: http://peer.berkeley.edu/smcat/index.html.
[43]
JGJ 3-2010, Technical specification for concrete structures for tall
building, Beijing: Ministry of Housing and Urban-Rural
Development of the People's Republic of China, 2010. (in Chinese)
[44] CECS
230:2008, Specification for design of steel-concrete mixed structure of tall
buildings, Beijing: China Institute of Building Standard Design & Research,
2008. (in Chinese)
List of Tables
Table 1.
The first nine vibration
modes of the super-tall building.
Table 2.
The relevant parameters
for the concrete modeling of the mega-columns
Table 3.
The failure criteria
for concrete and steel
List of Figures
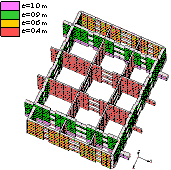
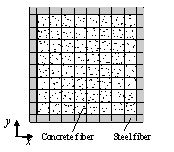
Figure 1.
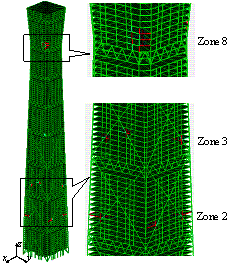
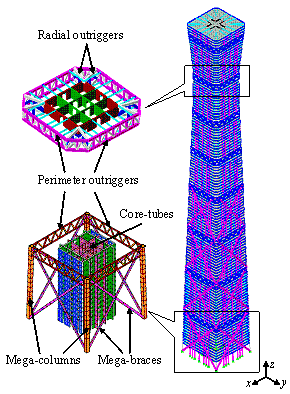
The FE model of the
super-tall building..
Figure 2.
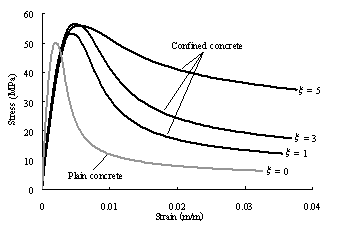
Typical stress-strain
curves for confined concrete.
Figure 3.
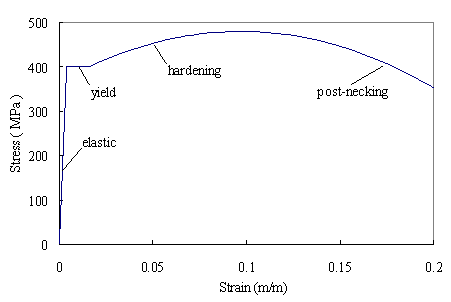
The stress-strain
backbone curve of the steel.
Figure 4.
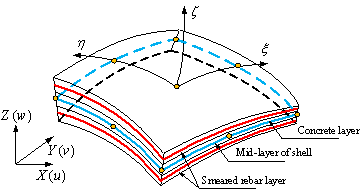
The schematic diagram
of the multi-layer shell element.
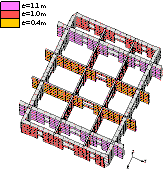
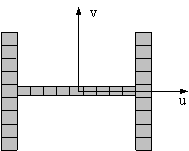
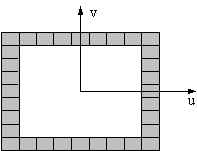
Figure 5.
The FE models of
typical core-tubes.
Figure 6.
The fiber-beam element
model for H-shaped or welded box-shaped steel beams.
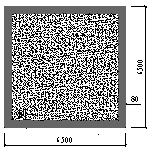
Figure 7.
Typical cross section
of the CFST columns (unit: mm).
Figure 8.
Fiber distributions
in a section of CFST column.
Figure 9.
The first nine vibration
modes of the super-tall building.
Figure 10.
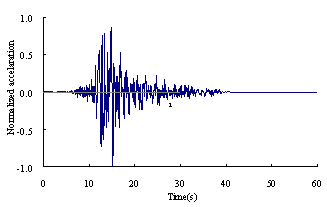
Dynamic characteristics
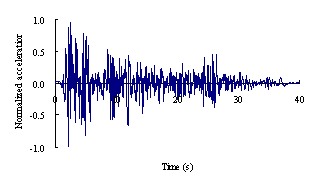
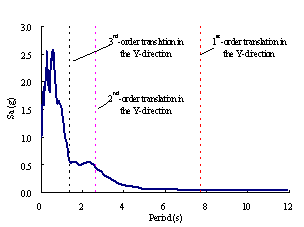
of El-Centro ground motion.
Figure 11.
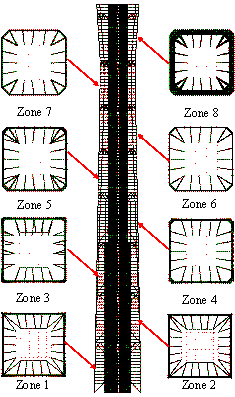
Distribution of plastic
zones under two different seismic intensities.
Figure 12.
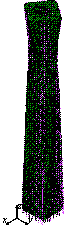
Typical collapse
mode of the super-tall building subjected to El-Centro ground motion (PGA
= 2940 cm/s2).
Figure 13.
Distributions of
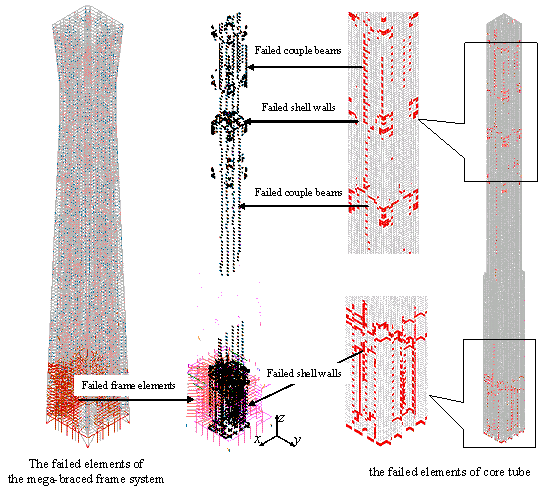
the failure elements.
Figure 14.
Overall collapse
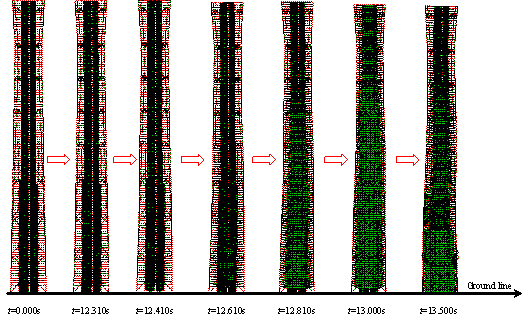
process of the super-tall building subjected to El-Centro ground motion in
the Y-direction (PGA = 2940 cm/s2).
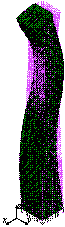
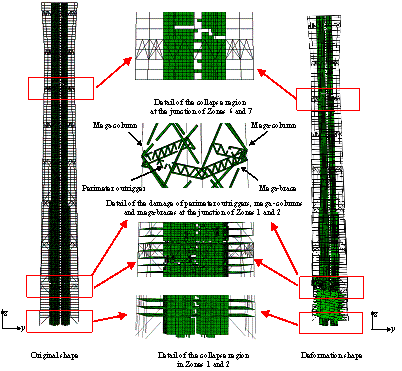
Figure 15.
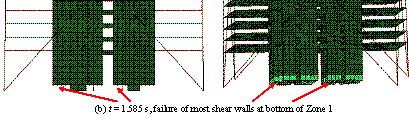
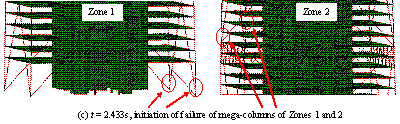
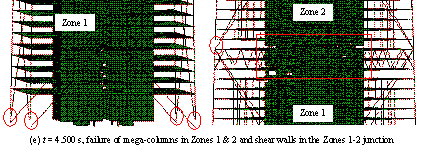
Collapse details
of the super-tall building subjected to El-Centro ground motion in the Y-direction
(PGA = 2940 cm/s2).
Figure 16.
The vertical and
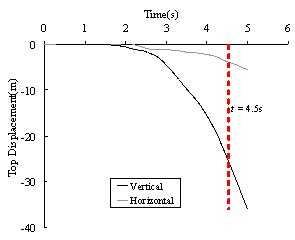
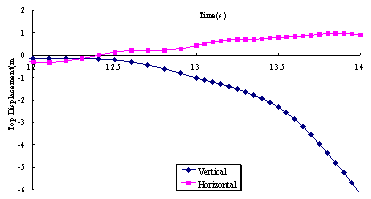
horizontal roof displacements of the super-tall building subjected to El-Centro
ground motion (PGA = 2940 cm/s2).
Figure 17.
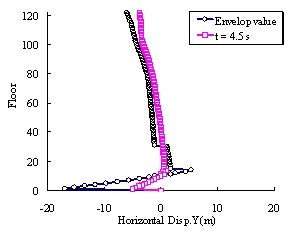
Distribution of horizontal
displacement along the structural height in Y-direction of the super-tall
building subjected to El-Centro ground motion (PGA = 2940 cm/s2).
Figure 18.
Dynamic characteristics
of KOBE ground motion.
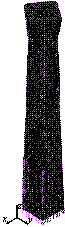
Figure 19.
Overall collapse
process of the super-tall building subjected to KOBE ground motion in the
Y-direction (PGA = 1764 cm/s2).
Figure 20.
The vertical and
horizontal roof displacement of the super-tall building subjected to KOBE
ground motion (PGA = 1764 cm/s2).
|
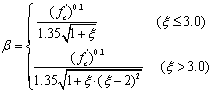 (4)
(4)