3.3 关键构件的应力-应变关系
结构倒塌过程是结构在地震作用下的宏观响应,为了进一步研究结构倒塌过程中关键构件力学行为,本节对关键构件的应力-应变行为进行了研究。在El-Centro地震动单向输入下计算得到的结构典型破坏部位如图13a所示。选取破坏部位的典型结构单元(图17),得到相应的倒塌过程中混凝土和钢材应力-应变滞回关系如图18至21所示。
对于巨柱单元,其在地震输入下受力过程的混凝土应力-应变滞回曲线如图18所示。显然,巨柱在整个破坏过程中,主要承受压应力,仅在较少时刻出现了拉应力,最终混凝土被压溃,巨柱发生压弯破坏;对于连梁,其在地震输入下受力过程的剪力与剪应变的关系如图19所示,最终发生剪切破坏;核心筒和伸臂桁架在地震输入下受力过程的应力-应变关系如图20和图21所示。
|
|
|
|
|
|
|
|
|
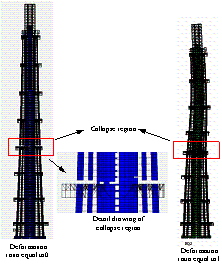
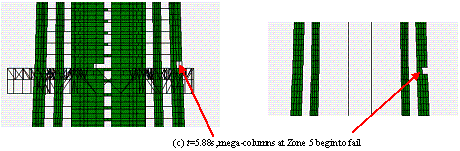
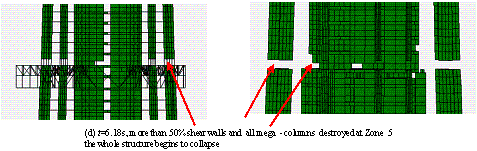
图14 El-Centro波单向地震动输入(PGA=19.6m/s2)倒塌过程
|
4 其他倒塌模式模拟
由于不同地震动输入的频谱成分差异较大,从而激发起的结构振动模态会有一定的差异,导致计算结果可能有较大差异。对于El-Centro波单向输入,结构在PGA=19.6m/s2(2G)时发生倒塌;而对于长周期成分比较丰富的日本Tha
San波,PGA=3.92m/s2(0.4G)
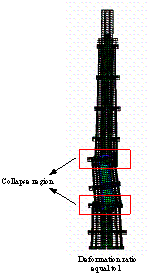
时结构就会发生倒塌;另外,地震动的输入形式(单向、双向和三向输入)对分析结果也存在较大的影响,例如对于上海人工波双向输入时,结构在PGA=9.8m/s2(1.0G)时就会发生倒塌,且结构倒塌破坏的模式也发上了一定程度的变化,其倒塌模式如图12b所示,详细的倒塌过程如图21所示。
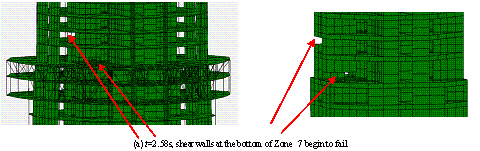
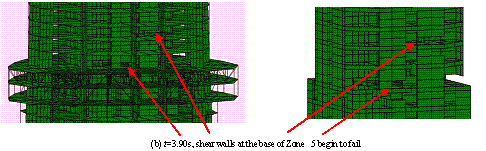
图22中上海人工波双向输入下的倒塌过程与图14中El-Centro波单向作用下的倒塌过程比较可知,两种倒塌模式的主要差别在于:在上海人工波双向作用下,结构在第5区段的巨柱和核心筒发生严重破坏后,第3区段也发生了严重破坏,最终结构折断成为三段(如图13b)。
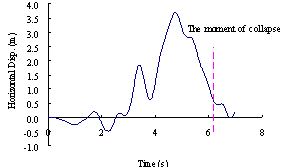
图15 El-Centro波(PGA=19.6m/s2)作用下结构顶点位移倒塌时程曲线
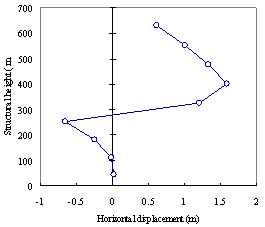

图16 El-Centro波(PGA=19.6m/s2)作用临近倒塌前结构位移分布
(a) 结构总位移沿高度分布; (b)巨型桁架间位移角分布
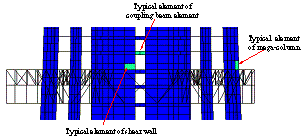
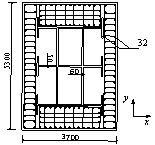
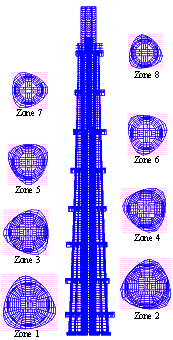
图17 结构代表性单元位置示意图
显然,除第5区段以外,第3区段也可能是结构的一个潜在薄弱部位。由此可见,由于该超高层结构冗余度较多,存在多条备用的荷载路径,且地震动本身的离散性大,使得超高层结构可能存在多种倒塌模式和多个可能的潜在薄弱部位。因此,要研究超高层结构地震倒塌机理,需对地震动频谱、输入方式等述问题加以综合考虑,方能得到比较合理的模拟结果。
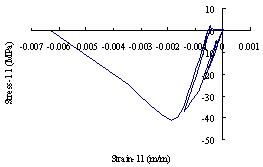
图18 典型破坏巨柱混凝土应力-应变关系
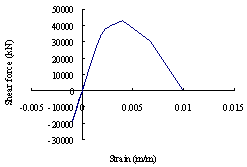
图19破坏连梁剪力-应变关系
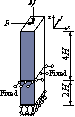
|
|
|
|
(a)
|
(b)
|
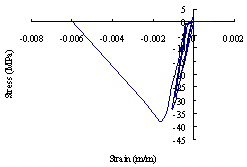
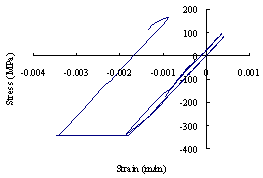
图20 核心筒的应力-应变关系
(a) 剪力墙中混凝土应力-应变关系; (b) 剪力墙中型钢的应力-应变关系
|
|
|
|
(a)
|
(b)
|
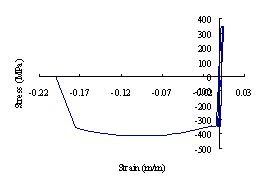
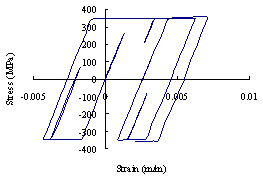
图21 伸臂桁架的应力-应变关系
(a) 破坏的伸臂桁架应力-应变关系; (b) 未发生破坏的伸臂桁架应力-应变关系
|

|

|
|

|

|
|

|

|
|

|

|
|
图22 双向地震动输入倒塌过程 上海人工波 X+Y方向输入(1:0.85),PGA=9.8m/s2
|
5 结论
汶川地震后,建筑结构、尤其重大建筑工程结构的抗倒塌性能成为结构抗震设计需考虑的重要问题。本文利用大型通用有限元MSC. MARC建立了结构总高度为632m的超高层结构——上海中心大厦的有限元模型,成功地对超高层建筑结构的倒塌过程进行了模拟。通过对该超高层结构倒塌模拟的研究,初步归纳出来以下结论:
(1) 基于有限元方法,选择合理的单元类型,材料本构和单元失效准则,能够实现复杂建筑结构的倒塌过程模拟;
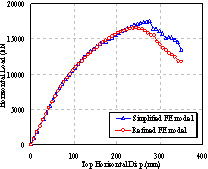
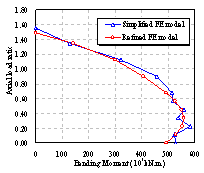
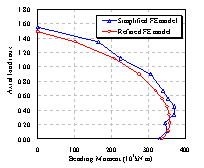
(2) 对于上海中心的巨柱,本文所提供的简化方法能比较好的把握构件的整体非线性性能,并能用较小的计算量达到较好的精度;
(3) 通过结构的倒塌分析,能够预测超高层结构的倒塌过程及机理,找出了结构的薄弱部位;
(4) 由于超高层结构冗余度较多,具备多条荷载传递路径,同时,地震动具有很大的不确定性,因此,结构存在多种可能的倒塌模式,如何合理地选择地震动记录进行倒塌分析还有待进一步的研究。
参考文献
1
陆华纲. 超高层筒体结构模型地震模拟振动台试验研究. 硕士论文, 大连: 大连理工大学, 2002
2
邹昀, 吕西林, 钱江. 上海环球金融中心大厦结构抗震性能研究. 建筑结构学报, 2006, 27(6):74-80
3
Li C S, Lam S S E, Zhang M Z, et al. Shaking table test of a 1: 20 scale high-rise building with a transfer
plate system. Journal of Structural Engineering, 2006,
132(11):1732-1744
4
毛苑君, 吕西林, 卢文胜, 等. 上海中心大厦结构模型振动台抗震试验. 土木建筑与环境工程,
2010, 32(Sup.2):534-536+549
5
黄庆华. 地震作用下钢筋混凝土框架结构空间倒塌反应分析. 博士论文,
上海: 同济大学,
2007
6
Yamada S, Suita K, Tada M, et al. Collapse experiment on 4-story steel
moment frame: part 1. Proceeding of 14th World Conference on Earthquake Engineering,
Beijing, China, 2008,October,12-17
7
Suita K, Yamada S, Tada, M, etal. Collapse experiment on 4-story steel
moment frame: part 2. Proceeding of 14th World Conference on Earthquake Engineering,
Beijing, China, 2008,October,12-17
8
van de Lindt J W, Pei S L, Pryor S E, et al. Experimental seismic response
of a full-scale six-story light-frame wood building. Journal of Structural Engineering-ASCE,
2010, 136(10):1262-1272
9
Wu C L, Kuo W W, Yang Y S, et al. Collapse
of a nonductile concrete frame: Shaking table tests. Earthquake Engineering and Structural
Dynamics, 2009, 38(2):205-224
10
陆新征, 江见鲸.
世界贸易中心飞机撞击后倒塌过程的仿真分析.
土木工程学报, 2001, 34(6): 8-10
11
Pan T C, Brownjohn J M W, You X T. Correlating
measured and simulated dynamic responses of a tall building to long-distance
earthquakes. Earthquake Engineering & Structural Dynamics, 2004, 33:611–632
12
Pekau O A, Cui Y. Progressive collapse simulation
of precast panel shear walls during earthquakes. Computers and Structures, 2006,
84(5-6): 400-412
13
Mattern S, Blankenhorn G, Breidt M. Comparison
of building collapse simulation results from finite element and rigid body models.
IUTAM Symposium on Multiscale Problems in Multibody System Contacts 2007; 257-267
14
Fan H, Li Q S, Alex Y T, et al. Seismic analysis of the world’s tallest building.
Journal of Constructional Steel Research, 2009, 65(5):1206-1215
15
丁洁民, 吴宏磊,
赵昕. 上海中心大厦罕遇地震抗震性能分析与评价.
土木建筑与环境工程, 2010, 32(Sup.2):231-233
16
陆新征, 叶列平,
缪志伟. 建筑抗震弹塑性分析.
北京: 中国建筑工业出版社,
2009. 9-38
17
江见鲸, 陆新征,
叶列平. 混凝土结构有限元分析.
北京: 清华大学出版社,2005.
47-53
18
汪训流, 陆新征,
叶列平. 往复荷载下钢筋混凝土柱受力性能的数值模拟.
工程力学, 2007, 24(12): 76-81
19
门俊, 陆新征,
宋二祥, 等.
分层壳模型在剪力墙结构计算中的应用.
防护工程, 2006, 28(3):9-13
20
林旭川, 陆新征,
缪志伟, 等. 基于分层壳单元的RC核心筒结构有限元分析和工程应用. 土木工程学报,
2009, 42(3): 51-56
21
缪志伟, 吴耀辉,
马千里, 等.
框架-核心筒高层混合结构的三维空间弹塑性抗震分析.
建筑结构学报, 2009, 30(4): 119-129
22
Spacone E, Filippou F, Taucer F. Fiber beam-column
modeling for non-linear analysis of R/C frames. Journal of Earthquake Engineering
and Structural Dynamics, 1996, 25(7): 711~725
23
秦从律, 张爱晖.
基于截面纤维模型的弹塑性时程分析方法.
浙江大学学报(工学版),
2005, 39(7): 1003~1008
24
Li Y, Lu X Z, Guan H, et al. An improved tie force method for progressive
collapse resistance design of reinforced concrete frame structures. Engineering
Structures, 2011, 33(10): 2931–2942
25
缪志伟, 陆新征,
王载, 等.
某钢框架偏心核心筒弹塑性分析.
四川建筑科学研究, 2008, 34(3): 5-10
26
陆新征, 张万开,
卢啸,等.
超级巨柱的弹塑性受力特性及其简化模型.
沈阳建筑大学学报(自然科学版),
2011, 27(3): 409-417
27
陆新征,
林旭川, 叶列平,
等. 地震下高层建筑连续倒塌的数值模型研究.
工程力学, 2010, 27(11): 64-70
28
GB50011-2010. 建筑抗震设计规范. 北京:中华人民共和国建设部
29
CECS 230-2008. 高层建筑钢—混凝土混合结构设计规程.
北京: 中国建筑标准设计研究院
|