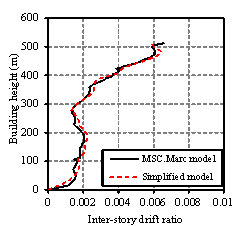
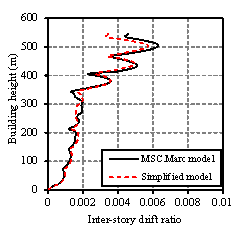
|
5.2 Total plastic energy dissipation
distribution along the building height
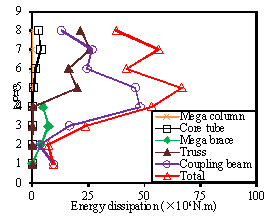
The total plastic hysteretic energy dissipation
distribution along the height of the building based on the half-braced scheme
is illustrated in Fig. 10 and is named the ¡°Total¡± curve. Because the lateral-force
resisting system significantly changes at Zone 5 (i.e., the mega braces installed
in the lower four zones no longer exist in the upper four zones), large deformations
and higher plastic energy dissipation are present in the upper 4 zones of
the building as opposed to the lower 4 zones. Furthermore, the dimensions
of the cross section of each floor gradually decrease from Zone 5 to Zone
6 and subsequently gradually increase from Zone 6 to Zone 7, thus leading
to more plastic energy dissipation in these zones compared to the lower 4
zones. As a result, these zones have the potential to suffer relatively severe
damage and are rather difficult to repair after an earthquake.
|
|
|
(a)
|
|
|
|
(b)
|
|
|
|
(c)
|
|
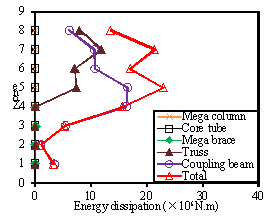
Fig. 10. Total plastic energy dissipation
distribution and plastic energy dissipation in different components
along the structural height of the half-braced scheme for different
seismic intensities: (a) PGA=220 gal. (b) PGA=310 gal.
(c) PGA=400
gal.
|
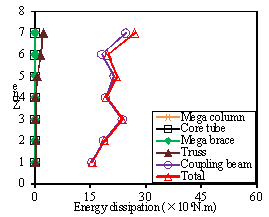
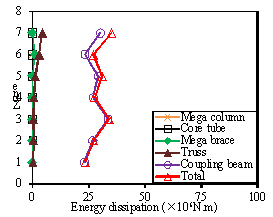
The total plastic hysteretic energy dissipation distribution along the height
of the fully braced scheme is illustrated in Fig. 11 and is also called the
¡°Total¡± curve. Because there are only 6 stories in Zone 8, the plastic hysteretic
energy dissipated in Zone 8 is combined with that in Zone 7 as a single zone
(i.e., Zone 7). Compared to the half-braced scheme, a relatively uniform distribution
of the total plastic energy is observed for the fully braced scheme. The following
two characteristics of fully braced scheme account for this difference: (1)
The mega braces are installed along the height of the entire building, which
leads to a more uniform distribution of the structural stiffness compared
to the half-braced scheme; (2) the strength-based design of the fully braced
scheme is more reasonable; as a result, the degree of nonlinearity in each
zone is approximately identical. Moreover, the maximum dissipated plastic
energy in a single zone of the fully braced is only 50.84% of that of the
half-braced scheme when PGA = 400 gal.
|

|
|
(a)
|
|
|
|
(b)
|
|
|
|
(c)
|
|
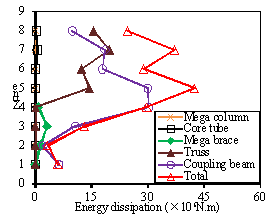
Fig. 11. Total plastic energy dissipation
distribution and plastic energy dissipation in different components
along the structural height of the fully braced scheme under different
seismic intensities: (a) PGA=220 gal.
(b) PGA=310 gal. (c) PGA=400
gal
|
The above discussions illustrate that the fully braced scheme induces a more
uniform plastic energy dissipation distribution compared to the half-braced
scheme. In addition, the fully braced scheme avoids severe damage concentration
in a single zone. All of these plastic energy dissipation characteristics
improve the performance of the building in terms of resiliency and enable
rapid recovery in the aftermath of a strong earthquake.
5.3 Plastic
energy dissipation contribution of each component along the building height
The average plastic energy dissipations in different
components along the height of the half-braced scheme are presented in Fig.
10 and are referred to as ¡°Mega column¡±, ¡°Core tube¡±, ¡°Mega brace¡±, ¡°Trusses¡±,
and ¡°Coupling beam¡± curves. Because the mega braces are only installed in
the lower 4 zones of the building, the plastic energy dissipated in the mega
braces is located in the lower 4 zones. In contrast, most of the plastic energy
is dissipated by the core tube, trusses and coupling beams located in the
upper 4 zones. Significant damage concentration in the coupling beams is observed
in Zones 4, 5 and 7, which means that the half-braced scheme does not make
full use of the energy dissipation capacity of all of the coupling beams along
the height of the building.
The average plastic energy dissipation contribution in different components
along the height of the fully braced scheme building is presented in Fig.
11. The trusses participated in the energy dissipation at the upper 3 zones
of the building. The results clearly indicate that the primary plastic energy
dissipation component is the coupling beams. In addition, the plastic energy
dissipated by coupling beams is uniformly distributed along the height of
the building, which avoids the concentration of damage.
As described above, the fully braced scheme induces a more uniform plastic energy
dissipation in the coupling beams along the building height compared to the
plastic energy dissipation of the half-braced scheme. The fully braced scheme
makes full use of the energy dissipation capacity of the coupling beams in
each zone of the building.
6. CONCLUSIONS
A 2D simplified model is developed for the seismic
analysis of a super-tall mega-braced frame-core tube building and applied
to compare two design schemes of this building in terms of resilience. The
following conclusions can be drawn:
(1) Compared to the refined FE model, the proposed
simplified model reduces the computational time by a factor of 100 while still
providing a reliable accuracy in predicting the seismic performances of the
two considered design schemes.
(2) The plastic energy dissipation characteristics
of both schemes are predicted and compared using the proposed simplified model.
The fully braced scheme is found to induce a uniform plastic energy dissipation
distribution and effectively enables the energy dissipation to be located
in readily replaceable components. In contrast, significant plastic energy
dissipation concentration is observed at the upper 4 zones of the half-braced
scheme, and the core tubes are found to suffer significant damage; as a result,
the functional recovery of the building will be delayed. Overall, the fully
braced scheme provides a better seismic resilient performance compared to
the half-braced scheme.
The outcome of this study will provide guidance and act as a reference for the
resilience-based earthquake design of super-tall buildings. The proposed simplified
model can be used to compare various design schemes at the preliminary design
stage.
ACKNOWLEDGEMENTS
The authors are grateful for the financial support
received from the National Natural Science Foundation of China (No. 51578320,
51261120377), the Beijing Natural Science Foundation (No. 8142024) and the
National Key Technology R&D Program (No. 2015BAK17B03).
REFERENCES
[1].
Almufti I, Willford M. Resilience-based earthquake
design initiative for the next generation of building. Rating System for the
Next Generation of Buildings 2014.
[2].
Takewaki I, Moustafa A, Fujita K. Improving the earthquake
resilience of buildings. Springer 2013.
[3].
Christopoulos C, Montgomery M. Viscoelastic coupling
dampers (VCDs) for enhanced wind and seismic performance of high-rise buildings.
Earthquake Engineering and Structural Dynamics 2013; 42(15): 2217-2233.
[4].
Resilient Washington State. A framework for minimizing
loss and improving statewide recovery after an earthquake. Washington State
Seismic Safety Committee Emergency Management Council 2012.
[5].
Giovinazzi S, Wilson T, Davis C, Bristow D, Gallagher
M, Schofield A. Lifelines performance and management following the 22 February
2011 Christchurch earthquake, New Zealand: Highlights of resilience. Bulletin
of the New Zealand Society for Earthquake Engineering 2011; 44(4).
[6].
Fan H, Li QS, Tuan Alex Y, Xu LH. Seismic analysis
of the world¡¯s tallest building. Journal of Constructional Steel Research
2009; 65(5):1206-1215.
[7].
Li QS, Zhi LH, Tuan AY, Kao CS, Su SC, Wu CF. Dynamic
behavior of Taipei 101 Tower: Field measurement and numerical analysis. Journal
of Structural Engineering 2010; 137(1): 143-155.
[8].
Poon DCK, Hsiao LE, Zhu Y, Joseph L, Zuo S, Fu GY,
Ihtiyar O. Non-linear time history analysis for the performance based design
of Shanghai Tower. Structures Congress 2011; 541-551.
[9].
Lu XL, Su NF, Zhou Y. Nonlinear time history analysis
of a super¨Ctall building with setbacks in elevation. The Structural Design
of Tall and Special Buildings 2013; 22(7): 593-614.
[10].
Jiang HJ, Fu B, Liu LE, Yin XW. Study on seismic
performance of a super-tall steel¨Cconcrete hybrid structure. The Structural
Design of Tall and Special Buildings 2014; 23(5): 334-349.
[11].
Li MK, Lu X, Lu XZ, Ye LP. Influence of soil¨Cstructure
interaction on seismic collapse resistance of super-tall buildings. Journal
of Rock Mechanics and Geotechnical Engineering 2014; 6(5): 477-485.
[12].
Lu XZ, Xie LL, Guan H, Huang YL, Lu X. A shear wall
element for nonlinear seismic analysis of super-tall buildings using OpenSees.
Finite Elements in Analysis and Design 2015; 98: 14-25.
[13].
Pan TC, Brownjohn JMW, You XT. Correlating measured
and simulated dynamic responses of a tall building to long-distance earthquakes.
Earthquake Engineering and Structural Dynamics 2004; 33(5): 611¨C632.
[14].
Lu XL, Zhu JJ, Zou Y. Study on performance-based
seismic design of Shanghai World Financial Center Tower. Journal of Earthquake
and Tsunami 2009; 3(4): 273-284.
[15].
ANSYS theory reference. Ansys Inc. 1999.
[16].
Perform-3D: Nonlinear analysis and performance assessment
for 3D structures: Version 4. Computers and Structures Inc 2006.
[17].
LS-DYNA theory manual. Livermore Software Technology
Corporation 2006; 3.
[18].
ABAQUS/standard: User¡¯s manual. Hibbett, Karlsson
& Sorensen Corporation 1998.
[19].
Fu F. Progressive collapse of high-rise building
with 3-D finite element modeling method. Journal of Constructional Steel Research
2009; 65(6): 1269-1278.
[20].
Lange D, Röben C, Usmani A. Tall building collapse
mechanisms initiated by fire: Mechanisms and design methodology. Engineering
Structures 2012; 36: 90-103.
[21].
Kotsovinos P, Usmani A. The World Trade Center 9/11
disaster and progressive collapse of tall buildings. Fire Technology 2013;
49(3): 741-765.
[22].
Jiang HJ, Lu XL, Liu XJ, He LS. Performance-based
seismic design principles and structural analysis of Shanghai Tower. Advances
in Structural Engineering 2014; 17(4): 513-528.
[23].
Jiang J, Chen LZ, Jiang SC, Li GQ, Usmani A. Fire
safety assessment of super tall buildings: A case study on Shanghai Tower.
Case Studies in Fire safety 2015; 4: 28-38.
[24].
Mazzoni S, McKenna F, Scott MH, Fenves GL. OpenSees
command language manual. Pacific Earthquake Engineering Research (PEER) Center
2006.
[25].
Lu X, Lu XZ, Zhang WK, Ye LP. Collapse simulation
of a super high-rise building subjected to extremely strong earthquakes. Science
China Technological Sciences 2011; 54(10): 2549-2560.
[26].
Lu XZ, Lu X, Guan H, Zhang Wk, Ye LP. Earthquake-induced
collapse simulation of a super-tall mega-braced frame-core tube building.
Journal of Constructional Steel Research 2013; 82: 59-71.
[27].
MSC.Marc User¡¯s manual. MSC Software Corporation,
Santa Ana, CA 2007.
[28].
Lu XL, Gong ZG, Weng DG, Ren XS. The application
of a new structural control concept for tall building with large podium structure.
Engineering Structures 2007; 29(8): 1833-1844.
[29].
Carpinteri A, Lacidogna G, Cammarano S. Structural
analysis of high-rise buildings under horizontal loads: A study on the Intesa
Sanpaolo Tower in Turin. Engineering Structures 2013; 56: 1362-1371.
[30].
Lu X, Lu XZ, Guan H, Ye LP. Collapse simulation
of reinforced concrete high-rise building induced by extreme earthquakes.
Earthquake Engineering and Structural Dynamics 2013; 42: 705-723.
[31].
Lee S, Tovar A. Outrigger placement in tall buildings
using topology optimization. Engineering Structures 2014; 74: 122-129.
[32].
Connor JJ, Pouangare CC. Simple-model for design
of framed-tube structures. Journal of Structural Engineering 1991; 117(12):
3623-3644.
[33]. Luco N, Cornell
CA. Structure-specific scalar intensity measures for near-source and ordinary
earthquake ground motions. Earthquake Spectra 2007; 23(2): 357- 392.
[34].
Meftah SA, Tounsi A, El-Abbas AB. A simplified approach
for seismic calculation of a tall building braced by shear walls and thin-walled
open section structures. Engineering Structures 2007; 29(10): 2576-2585.
[35].
Lu X, Lu XZ, Sezen H, Ye LP. Development
of a simplified model and seismic energy dissipation in a super-tall building.
Engineering Structures 2014; 67: 109-122.
[36].
GB50011-2010. Code for seismic design of buildings.
Beijing: Ministry of Housing and Urban-Rural Development of the People¡¯s Republic
of China 2010.
[37].
JGJ 3-2010. The Technical Specification for Concrete
Structures for Tall Buildings. Beijing: Ministry of Housing and Urban-Rural
Development of the People¡¯s Republic of China 2010.
[38].
Lu XZ, Ye LP, Miao ZW. Elasto-plastic analysis of
buildings against earthquake. Beijing: China Architecture & Building Press
2009. [in Chinese].
[39].
Habibullah A. ETABS-Three dimensional analysis of
building systems, User manual. Computers and Structures Inc 1997.
[40]. FEMA P695: Quantification
of building seismic performance factors. Applied Technology Council, Redwood
City, C.A 2009.
[41].
Fortney PJ, Shahrooz BM, Rassati GA. Large-scale
testing of a replaceable ¡°fuse¡± steel coupling beam. Journal of Structural
Engineering 2007; 133(12): 1801-1807.
[42].
Chen Y, McFarland DM, Wang Z, Spencer BF, Bergman LA. Analysis of
tall buildings with damped outriggers. Journal of Structural Engineering 2010;
136(11): 1435-1443.
[43].
Zhou Y, Zhang CQ, Lu XL. Earthquake resilience of
a 632-meter super-tall building with energy dissipation outriggers. Proceeding
of the 10th National Conference on Earthquake Engineering, Earthquake Engineering
Research Institute, Anchorage, AK, 2014.
[44].
Chen CH. Performance-based seismic demand assessment
of concentrically braced steel frame buildings. Ph.D. Dissertation, University
of California, Berkeley, USA 2010.
List of Tables
Table 1.
Primary differences between the fully braced scheme
and half-braced scheme
Table 2.
Reduction in period of the two models (%) when the
component stiffness is reduced by 50%
Table 3.
Typical values of the hysteretic parameters of different
components
Table 4.
Comparison of the first six translational periods
(in seconds) from the simplified and refined FE MSC.Marc models
Table 5.
Plastic energy dissipation contribution of different
structural components under different earthquake intensities
List of Figures
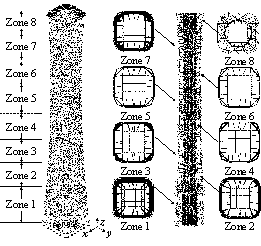
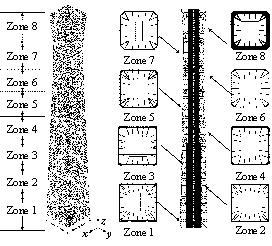
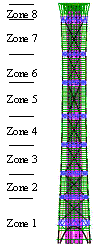
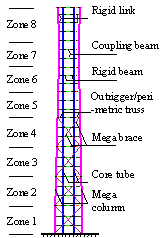
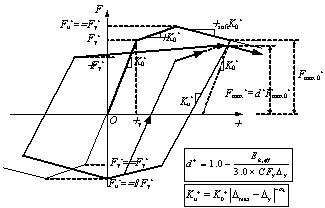
Fig. 1.
Fully braced scheme
Fig. 2.
Half-braced scheme
Fig. 3.
Refined FE models of two structural schemes
Fig. 4.
Refined FE model and simplified model of the fully
braced scheme
Fig. 5.
Refined FE model and simplified model of the half-braced
scheme
Fig. 6.
Distribution of the coupling beams in typical RC
core tubes
Fig. 7.
Hysteretic component model used in this research
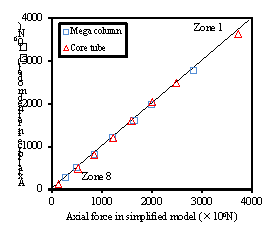
Fig. 8.
Comparison of the axial forces in mega columns and
core tubes of the simplified and refined models
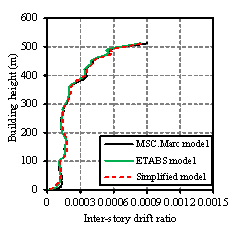
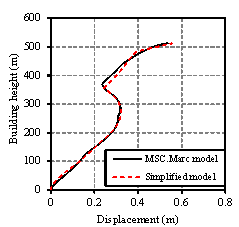
Fig. 9.
Comparison of the time history analysis
results between the simplified and refined FE models
Fig. 10.
Total plastic energy dissipation distribution and
plastic energy dissipation in different components along the structural height
of the half-braced scheme for different seismic intensities
Fig. 11.
Total plastic energy dissipation
distribution and plastic energy dissipation in different components along
the structural height of the fully braced scheme under different seismic intensities
Correspondence to: Xinzheng
Lu, Department of Civil Engineering, Key Laboratory of Civil Engineering Safety
and Durability of China Education Ministry, Tsinghua University, Beijing,
P.R. China. E-mail: luxz@tsinghua.edu.cn
|