Quantifying the Seismic Resilience of Two Tall Buildings Designed Using Chinese and US Codes

Yuan Tian¹, Xiao Lu², Xinzheng Lu^{* [3]} , Mengke Li¹, Hong Guan⁴

¹ Beijing Engineering Research Center of Steel and Concrete Composite Structures, Tsinghua University, Beijing P. R. China

²Department of Civil Engineering, Beijing Jiaotong University, Beijing, P.R. China

³ Key Laboratory of Civil Engineering Safety and Durability of China Education Ministry, Department of Civil Engineering, Tsinghua University, Beijing, P.R. China

⁴Griffith School of Engineering, Griffith University Gold Coast Campus, Queensland 4222, Australia

(Received   Jan. 19, 2016   , Revised   May, 16, 2016   , Accepted   Aug. 02, 2016   )

Earthquakes and Structures, 2016, 11(6): 925-942.

DOI: 10.12989/eas.2016.11.6.925

Download Full Text PDF

Abstract.  With ongoing development of earthquake engineering research and the lessons learnt from a series of strong earthquakes, the seismic design concept of ※resilience§ has received much attention. Resilience describes the capability of a structure or a city to recover rapidly after earthquakes or other disasters. As one of the main features of urban constructions, tall buildings have greater impact on the sustainability and resilience of major cities. Therefore, it is important and timely to quantify their seismic resilience. In this work, a quantitative comparison of the seismic resilience of two tall buildings designed according to the Chinese and US seismic design codes was conducted. The prototype building, originally designed according to the US code as part of the Tall Building Initiative (TBI) Project, was redesigned in this work according to the Chinese codes under the same design conditions. Two refined nonlinear finite element (FE) models were established for both cases and their seismic responses were evaluated at different earthquake intensities, including the service level earthquake (SLE), the design-based earthquake (DBE) and the maximum considered earthquake (MCE). In addition, the collapse fragility functions of these two building models were established through incremental dynamic analysis (IDA). Based on the numerical results, the seismic resilience of both models was quantified and compared using the new-generation seismic performance assessment method proposed by FEMA P-58. The outcomes of this study indicate that the seismic resilience of the building according to the Chinese design is slightly better than that according to the US design. The conclusions drawn from this research are expected to guide further in-depth studies on improving the seismic resilience of tall buildings.

Keywords:  performance-based design method; seismic loss; resilience; tall building; design codes

1. Introduction

With ongoing development of earthquake engineering research and the lessons learnt from a series of strong earthquakes, the seismic design concept of ※resilience§ has drawn increasing attentions worldwide (Mieler et al. 2013, Jacques et al. 2014). The term ※resilience§ has been used in many disciplines (Chang and Shinozuka 2004, Rose 2004, Dec辰 et al. 2013). ※Resilience§ was defined in PPD-8 (2011) as ※the ability to adapt to changing conditions and withstand and rapidly recover from disruption due to emergencies§. This concept was further expanded in PPD-21 (2013) to include ※the ability to prepare for and adapt to changing conditions and to withstand and recover rapidly from disruptions§. Bruneau et al. (2003) defined the seismic resilience as ※the ability of social units (e.g., organizations, communities) to mitigate hazards, contain the effects of disasters when they occur, and carry out recovery activities in ways that minimize social disruption and mitigate the effects of future earthquakes§.

After Christchurch was devastated by earthquake in 2011, none of the 51 tallest buildings in the city collapsed owing to the rigorous seismic standards of New Zealand. Nonetheless, 37 of these tall buildings had to be demolished due to their severe damage and potentially high costs to repair, leading to enormous economic loss and negative social impact (Wikipedia Contributors 2015). Therefore, the seismic design concept of ※resilience§ for tall buildings has become vitally important for modern scientific community. In this regard, many studies have been conducted in relation to the seismic resilience of buildings and healthcare systems (Cimellaro et al. 2010, Biondini et al. 2015). At the UN World Conference on Disaster Risk Reduction in 2015, the UN Development Programme (UNDP) announced a new 10-year global program to support the national efforts in reducing the risks of disasters. The program, named ※5-10-50§, is expected to provide a strong support to 50 countries and communities over 10 years in delivering better risk-informed development. The ※resilient recovery§ was also listed as one of the five strategic areas on which the program will focus (UNDP 2015).

Rapid global urbanization has seen tall buildings being an important part of the urban construction. The seismic resilience of tall buildings has become a critical issue in sustainable urban development due to the dense population and property they contain. Currently, significant progress has been made in relation to the seismic performance of tall buildings through long-term research projects. For example, Lu et al. (2011, 2013a) studied the collapse resistance of several typical super-tall buildings using the finite element (FE) method. The outcome of their work has assisted in the design optimization of those buildings (Lu et al. 2016a). In addition, extensive studies (Lu et al. 2007, Fan et al. 2009, Poon et al. 2011, Takewaki and Tsujimoto 2011, Chang et al. 2013, Kim and Lee 2013, He et al. 2014, Jiang et al. 2014, Lu et al. 2013b, 2014, 2015a, 2016b) on structural seismic performance have been performed for tall and super-tall buildings through experiments and numerical simulation, providing valuable practical advices on seismic design. The research mentioned above shows that the structural seismic performance of tall buildings, especially of frame-shear wall and frame-core tube buildings, can meet the safety requirements set by the design standards.

Nevertheless, to achieve the objective of resilience, the structures are required not only to sustain a state of safety in earthquakes but also to be prepared for post-earthquake recovery to ensure continued operation and functionality immediately thereafter (Almufti and Willford 2013). Therefore, it is important to gather accurate information on the repair costs and repair time of the buildings under earthquakes. In the conventional performance-based seismic design, the seismic performance of the structural components was normally considered in detail, but that of the nonstructural components was often neglected. Note that earthquake-induced repair costs of nonstructural components and contents of modern tall buildings usually account for more than 50% of the total cost, due to the increasing expenses of these components (Liu and Jiang 2013). For example, during the 1994 Northridge earthquake, nonstructural damages accounted for 50% of the total loss (i.e., approximately $18.5 billion of building damage) (Kircher 2003). Therefore, to achieve a better prediction on the seismic losses of buildings in earthquakes, all structural components and nonstructural contents of buildings should be considered. To address this issue, the next generation performance-based seismic design method (i.e., FEMA P-58 Seismic Performance Assessment of Buildings, Methodology and Implementation) (referred to as ※FEMA P-58 method§ hereafter), was proposed by the Federal Emergency Management Agency (FEMA) and the Applied Technology Council (ATC) of the United States (US) (FEMA 2012a, b). An associated software (i.e., Performance Assessment Calculation Tool (PACT)), was also provided to facilitate the implementation of the FEMA P-58 method. Based on this method, the repair costs, repair time and casualties of buildings under earthquakes can be readily obtained, and such information can also be easily understood by the stakeholders. For this reason, the FEMA P-58 method is adopted in this work.

China and the US have constructed a large number of tall buildings. Both countries have also developed well-accepted seismic design codes according to their own practical conditions. Therefore, it is a very meaningful task to make a thorough comparison of the seismic performance of tall buildings designed according to the Chinese and the US codes. Recently, Lu et al. (2015b) compared the seismic designs of two typical reinforced concrete (RC) frame-core tube buildings based on the Chinese and US codes, which has provided valuable references to the structural design of tall buildings. Nonetheless, while the structural seismic performance of these tall buildings has been systematically investigated by Lu et al. (2015b), damage of nonstructural components and building contents were not considered. Therefore, the work of Lu et al. (2015b) was extended in this study where a quantitative comparison of the seismic resilience of the two RC frame-core tube buildings were conducted using the FEMA P-58 method. Generally, a resilient system exhibits reduced failure probabilities, reduced consequences from failures (in terms of life loss, damage, and negative economic and social consequences), and reduced time to recovery (Bruneau et al. 2003). These three key features are critical in assessing the seismic resilience of building systems. For this reason, seismic resilience of tall buildings was quantified in this work based on these three features. In Section 4.1, the failure probabilities of the buildings were quantified through the collapse fragility curves obtained from IDA. In Section 4.2, the consequences from failures were elaborated in terms of the repair costs and casualties. In Section 4.3, the time to recovery was illustrated in some detail. The conclusions drawn from this research are expected to guide further in-depth studies on improving the seismic resilience of tall buildings.

2. Seismic design information of the case study buildings

To improve the practical applications of the performance-based seismic design methods for tall buildings, the Pacific Earthquake Engineering Research Center (PEER) has launched the TBI research plan (TBI 2010), conducted thorough investigations on the seismic design of tall buildings, and provided a few representative engineering cases for researchers undertaking further studies. One of the cases is a 42-story RC frame-core tube building with a height of 141.9 m above the ground, as shown in Fig. 1(a). The building designed to the US code is named ※Building 2A§. Through a thorough investigation, Lu et al. (2015b) indicated that the seismic hazard of Building 2A was practically equivalent to the 8.5 degree seismic intensity zones specified in the Chinese seismic design code (with a peak ground acceleration (PGA) of 0.30 g at a 10% probability of exceedance at the 50-year hazard level). Subsequently, based on the specific design information, Building 2A was redesigned according to the Chinese codes (Lu et al. 2015b), named ※Building 2N§. Detailed information of Buildings 2A and 2N, documented in Lu et al. (2015b), indicates that although both buildings have an equivalent seismic hazard level, they differ significantly due to the differences between the seismic design methods of China and the US, as given below.

(1) Building 2N has more internal walls in the core tube and larger columns (Fig. 1). The seismic design forces determined by the Chinese response spectrum are larger than the US counterparts at the same seismic hazard level. In addition, a more rigorous requirement for the story drift ratio is specified in the Chinese codes, thereby resulting in larger seismic design forces. These two aspects lead to a larger lateral stiffness and a higher level of material consumption (concrete and reinforcement) of Building 2N than those of Building 2A as shown in Fig. 2.

(2) Nonlinear time history analysis (THA) was performed by Lu et al. (2015b) for these two buildings using the 22 far-field ground motion records recommended by FEMA (2009). The corresponding PGA values of these selected ground motions were scaled to 0.11 g, 0.30 g and 0.51 g (i.e., the corresponding PGAs at respectively 63.2% (SLE), 10% (DBE) and 2% (MCE) probability of exceedance at 50-year hazard level defined in the Chinese codes (GB50011-2010 2010)). The mean values and standard deviations of story drift ratio and floor acceleration of Buildings 2A and 2N subjected to these ground motions are presented in Fig. 3 and 4. The two buildings are found to perform similarly, except that the deformation of Building 2N is slightly smaller due to the more rigorous serviceability requirements of the Chinese codes.

The foregoing comparison indicates that Building 2N (designed following the Chinese codes) demonstrates a larger stiffness and a smaller deformation under earthquakes and exhibits better structural seismic performance. On the other hand, the Chinese design results in a larger amount of steel and more structural components. Thus, it is challenging to evaluate the Chinese and the US designs based purely on the structural seismic performance and the construction costs. A thorough performance-based evaluation is therefore required to quantify the seismic resilience of these two buildings.

3 Quantification method for seismic resilience

As mentioned in Section 1, the three key features of resilient systems (i.e., reduced failure probabilities, reduced consequences from failures and reduced time to recovery (Bruneau et al. 2003)) are considered herein to quantify the resilience and performance of the two buildings. This presents an important scientific advancement to the traditional seismic performance evaluation based on engineering demand parameters (EDPs) (e.g., story drift ratio, floor acceleration, shear force, et al.). Furthermore, the relevant evaluation results are can be very easily understood by the building owners and government authorities.

The failure probabilities can be accurately assessed based on the collapse fragility curves of the structures obtained from IDA, which will be discussed in Section 4.1 in detail. Notably, the major challenge to quantify the seismic resilience is to acquire the accurate information of the repair costs and repair time for the buildings. Such information cannot be obtained through conventional THA. Instead, the FEMA P-58 method is used herein to determine the seismic losses and the repair time. The basic procedure of the FEMA P-58 method is illustrated in Fig. 5.

Various parameters are needed to calculate the casualties, losses and repair times. Note that the parameter values given in FEMA P-58 are determined statistically according to the practical conditions of America and may be quite different from those of China. Notwithstanding, to ensure comparability of these two buildings and facilitate understandability of the outcomes, the parameters recommended by FEMA P-58 are adopted herein for both buildings.

To enable researchers to conveniently implement the seismic loss assessment procedure, an associated software PACT (Performance Assessment Calculation Tool) has been developed (FEMA 2012b) to facilitate the implementation of the FEMA P-58 method in the modeling and analysis tasks. PACT is also adopted in this study to predict the seismic losses (repair costs, repair time and casualties) of Buildings 2A and 2N. Note that detailed definition of the parameters mentioned below can be found in FEMA (2012a). The main analysis steps of PACT are:

Step 1 (basic project information): the region cost multiplier and date cost multiplier should be defined according to the actual conditions, which will be used to modify the consequence function of repair costs due to different regions and inflation. As the present study focuses on the comparison of seismic losses of tall buildings designed according to different codes, the discrepancies in cost caused by different regions and inflation are ignored. For this reason, both multipliers are set to 1.0.

Step 2 (building information): certain building parameters, such as the number of stories, core and shell replacement cost, total replacement cost, and replacement time, must be defined. The core and shell components include the basic building structure and cladding, and all nonstructural components that are not typically provided by the tenants, such as elevators, stairs, toilet rooms, and basic electrical and mechanical services. The core and shell replacement costs are required to replace all building core and shell items, including an allowance for building demolition and site clearance. The total replacement cost covers the cost of core and shell constituents plus the cost to replace tenant improvements and contents. The tenant improvements commonly involve office partitions, ceilings, light fixtures, heating, ventilation and air conditioning (HVAC), and electrical distribution within occupied spaces except in common areas, such as lobbies or central plants. Moehle et al. (2011) and Davis Langdon (2010) provided, respectively, the core and shell replacement cost and the total replacement cost, and a list of cost items for Building 2A. Because of the identical building layout and occupancy function, all corresponding costs for Building 2N are assumed to be the same as for Building 2A, except for the cost incurred by the amount of structural material consumption. According to Comerio and Blecher (2010) and Comerio (2000), a replacement time of 1500 days is adopted for both buildings. According to the recommended value given in FEMA P-58 Volume 2 (FEMA 2012b), the height factor, which is used to reflect the increases in the repair cost attributable to loss of efficiency due to working in high stories and the additional cost incurred by the corresponding material transport and protection measures, is set to be 1.00 for stories 1 to 4, 1.08 for stories 5 to 10, and 1.16 for story 11 and higher. The hazmat factor, reflecting the additional cost due to various hazardous material premiums, is taken to be 1.0. The occupancy factor, referring to as the additional cost of working around ongoing building operations, equipment, and the collateral protection required for some construction characteristics, varies with the occupancy category. Here, the occupancy factor is set to 1.2 for retail and 1.1 for residential categories (FEMA 2012b). The other factors are taken to be default.

Step 3 (population model): the population model is the distribution of occupants within the building at various times of the day and is used for casualty assessment. The population models provided in PACT are used. The retail population model is used for story 1, and the residential population model is used for stories 2 to 42 following Moehle et al.＊s (2011) work.

Step 4 (component fragility specifications and performance groups): PACT provides a dataset of more than 700 individual fragility specifications, containing both structural and nonstructural components. Typically, the peak story drift ratio and/or the peak floor acceleration are used to determine whether a component is damaged. In the present study, the number of structural components is calculated according to the actual situation. The number of nonstructural components is estimated using the Normative Quantity Estimation Tool provided by FEMA P-58. Note that the nonstructural components of the two buildings are assumed to be the same due to the same building layout and occupancy function. The fragility specifications of the structural and nonstructural components for Buildings 2A and 2N are given in Appendix A.

Step 5 (collapse fragility and mode): the median value q and the dispersion value b of the collapse fragility curve, the collapse mode, and the fatality and injury rate of the building are required. Using the IDA method, the collapse fragility curves of Buildings 2A and 2N can be obtained (Fig. 6). Subsequently, the parameters of the collapse fragility curves can be determined as summarized in Table 1. According to FEMA (2008), the mean fatality rate and the mean injury rate are set to 10% and 90%, respectively, and the default value of 0.5 is used for the associated COV.

Table 1 Parameters of collapse fragility curves for Buildings 2A and 2N

Step 6 (structural seismic analysis results): according to the selected fragility specifications, the demand parameters to be considered include the peak story drift ratio, the peak floor acceleration, and the peak coupling beam rotation. These parameters have been determined by Lu et al. (2015b) through a nonlinear THA for Buildings 2A and 2N using the 22 recommended (FEMA 2009) far-field ground motion records with PGAs of 0.11 g, 0.30 g and 0.51 g. These parameters are subsequently inputted into PACT.

Step 7 (residual drift fragility): the residual drift fragility represents the probability that for a given value of residual story drift ratio, the building will be repaired. According to Lu et al. (2015b), the obtained residual drifts under the aforementioned three earthquake intensity levels are found to be fairly small. As such, the residual drift fragility is neglected in this work.

4 Comparison of the seismic resilience

In this section, the comparison of the seismic resilience of Buildings 2A and 2N is performed based on the three key features of a resilient system (i.e., reduced failure probabilities, reduced consequences from failures and reduced time to recovery). Comparison results and discussion are provided in relation to each feature, and an overall analysis is presented in Section 5.

4.1 Failure probabilities

To quantify the failure probabilities, the IDA is used in this work. This concept was initially introduced by Bertero (1977), and further confirmed by Vamvatsikos and Cornell (2002). The IDA method has been widely used in investigating the seismic performance of structures (Bazzuro and Cornell 1994a, b, Christovasilis et al. 2009, Asgarian et al. 2010, Eads et al. 2013, Hemsas et al. 2014, Nazri and Ken 2014, Shi et al. 2014). The IDA method refers to the structural system subjecting to a set of earthquake ground motions, each of which is being incrementally scaled to multiple levels of intensity. The nonlinear THA is implemented until dynamic instability is reached. Then, the probability of collapse at a given intensity level is estimated as the proportion of records causing collapse among the set of records selected at the given level. The collapse fragility curve is a plot illustrating how the probability of collapse increases with increased ground motion intensities (Eads et al. 2013). It also provides the cumulative distribution of collapse intensities from selected records in the IDA. Hence, the failure probabilities are assessed in this work based on the collapse fragility curves of the structures obtained from IDA.

As shown in Fig. 6 and Table 1, the collapse fragility curves of Buildings 2A and 2N are provided based on the IDA method. The collapse margin ratio (CMR) is used herein to quantitatively assess the collapse resistance of these two buildings (FEMA 2009). The values of CMR are 7.86 for Building 2A and 8.35 for Building 2N. The failure probabilities of these two buildings under MCE are both very close to 0. In addition, the results indicate that both buildings have sufficient collapse resistance, with Building 2N exhibiting slightly better performance.

4.2 Repair costs and casualties

Despite the fact that there are many types of seismic losses, only the direct seismic losses (i.e., the repair costs and casualties) are considered herein due to the complexity of other indirect losses. Following the FEMA P-58 method mentioned above, the repair costs and casualties of Buildings 2A and 2N under earthquakes are evaluated qualitatively. Three earthquake intensities (i.e., SLE, DBE and MCE of the 8.5 degree seismic intensity zones given in the Chinese codes) are selected. According to FEMA P-58 Volume 1 (FEMA 2012a), the sample number of the Monte Carlo method is set to 1000. The simulation results show that no collapse occurs during the Monte Carlo analysis, which also indicates that both buildings have sufficient seismic safety. Detailed comparison results are illustrated below.

4.2.1 Repair costs

The median repair costs of Buildings 2A and 2N at three different earthquake intensities are shown in Fig. 7. By definition, the summation of the median structural and nonstructural component repair costs may not be equal to the median total repair costs. From Fig. 7, the following results can be obtained.

(1) At all three earthquake intensities, the repair costs of the nonstructural components account for the majority of the total. At the SLE and DBE levels, seismic losses caused by the structural components are very small, which means that the performance of these buildings meets the corresponding code requirements. At the MCE level, the losses in the structural components increase significantly.

(2) At all three earthquake intensities, the repair costs of the nonstructural components in Building 2A are larger than those in Building 2N.

(3) At the SLE and DBE levels, the total repair costs mainly depend on the damage to the nonstructural components. According to Lu et al. (2015b), the stiffness of Building 2N is larger than that of Building 2A due to the more rigorous serviceability requirements set by the Chinese codes, leading to a smaller inter-story drift in Building 2N. Thus, the total repair costs of Building 2N are smaller.

(4) At the MCE level, severe damage occurs in the structural components, leading to higher corresponding repair costs. In addition, there are more structural components (more internal walls, coupling beams and frame beams) in Building 2N. Consequently, the repair costs of the structural components of Building 2N are larger, and the discrepancies in the total repair costs decreases between Buildings 2A and 2N.

The repair costs of different components at the three earthquake intensities are presented in Fig. 8. As the summation of median structural and nonstructural component repair costs does not equal the median of the total costs, Fig. 8 shows the mean values of the Monte Carlo simulation. The following results can be obtained from Fig. 8.

(1) At the SLE level, the repair costs are mainly caused by the damage to the HVAC, the partitions and the wall finishes. In the HVAC, the chillers, cooling towers, and compressors, which are acceleration-sensitive components, contribute the largest proportion to the total losses. The nonlinear THA indicates that the roof acceleration of Building 2A is larger (Fig. 4). Thus, the repair cost proportion of HVAC in Building 2A is larger than that in Building 2N.

(2) At the DBE level, the HVAC, the partitions and the wall finishes still contribute the most to the total repair costs, yet the damage in the shear walls and coupling beams cannot be neglected. Some losses are also caused by the damage in ceilings and elevators.

(3) At the MCE level, the proportion of the repair costs of the HVAC decreases, whereas the repair costs of other components increase. Among the nonstructural components, the exterior enclosure, ceilings and elevators occupy a larger proportion. Among the structural components, all the moment frame joints, flat slab每column joints, shear walls and coupling beams experience a certain degree of damage, and the repair costs of the shear walls contribute the most. The repair cost proportion of the moment frame joints, shear walls and coupling beams in Building 2N is larger than that in Building 2A because of the larger number of internal walls, coupling beams and frame beams and the larger span每depth ratio of the coupling beams in Building 2N. This conclusion agrees with the higher repair costs in the structural components of Building 2N shown in Fig. 7.

4.2.2 Casualties

At the SLE and DBE levels, no casualties are found in the two buildings. The extent of casualties at the MCE level is given in Table 2. The casualty number is very small and close to 0. The casualties are mainly caused by the falling of the suspended ceilings and the damage to the elevators. Therefore, more attention should be paid in the design and construction of the nonstructural components.

Table 2 Casualties of Buildings 2A and 2N under severe earthquakes

4.3 Repair time

Downtime, an important aspect of resilience, is the time required to achieve a defined recovery state after an earthquake has occurred (Almufti and Willford 2013). In addition to the repair time, the delay between the earthquake event and the initiation of repairs, referred to as the ※impeding factors§, is also a part of downtime. As the present study focuses on the seismic resilience comparison between the two tall buildings, the impeding factors are not considered essential for the purpose of this study. Thus, only the repair time of the two buildings is considered herein. The repair time is characterized by the number of workdays required for building restoration. One workday represents the labor quantity of one worker in one day. At the three different earthquake intensities, the median values of the repair workdays are displayed in Fig. 9, and the following outcomes can be obtained:

(1) Similar to the findings on the repair costs, the median repair time of the nonstructural components contributes the most to the total cost because significant damage occurs in the nonstructural components.

(2) At the SLE and DBE levels, the repair workload of the structural components is small. However, it increases significantly at the MCE level. At the SLE and DBE levels, when the nonstructural components dominate the repair time, the median repair workload of Building 2A is larger than that of Building 2N. However, at the MCE level, the repair workload of Building 2N becomes larger. This is mainly due to the increase of damage to the structural components and the fact that Building 2N has more structural components. Note that more time is usually required to repair the structural components than the nonstructural ones.

Fig. 10 shows the distribution of the median repair workload of Buildings 2A and 2N, leading to the following findings.

(1) At the SLE level, the inter-story drift of the lower stories is smaller. Only story 27 and higher require to be repaired to some extent. The maximum of the median repair workload takes place at the top of the building due to the more vulnerable contents (chillers, cooling towers, and compressors) there. The median repair workload of Building 2N is smaller due to the smaller inter-story drift and peak floor acceleration than those of Building 2A (Fig. 3 and 4).

(2) At the DBE level, all stories were damaged and must be repaired. In addition, a larger median repair workload appears on the higher stories. The median repair workload at the top of the building is the largest, and the corresponding value of Building 2A is larger than that of Building 2N. Furthermore, the median repair workload at the bottom story is the second largest because of the damage to the elevators, which is assumed to be at the bottom of the building when the earthquake occurred. The shear walls, the partitions and the wall finishes are displacement sensitive. Therefore, their damage states are dependent on the inter-story drift. In this assessment, these components account for the second-largest proportion of the total repair workload (the HVAC takes the largest proportion). According to Fig. 3, Building 2A has a larger inter-story drift at the higher stories, whereas Building 2N has a larger inter-story drift at the lower stories. The distribution of the inter-story drift in Building 2N is more uniform. Therefore, the median repair workload at the higher stories of Building 2A is larger, whereas the repair workload at the lower stories of Building 2N is larger. The distribution of the repair time is more uniform in Building 2N.

(3) At the MCE level, compared to the results at the DBE level, the damage becomes more severe, whereas the repair workload distribution along the height remains similar. The median repair workload at the higher stories is larger than that at the lower stories, and the maximum value appears at the top story and the bottom story. Building 2A has a larger median repair workload at the higher stories, whereas Building 2N has a larger median repair workload at the lower stories and more uniform distribution of the repair time along the height. The causes of these phenomena are similar to those at the DBE level.

5 Conclusions

The seismic resilience of two RC frame-core tube buildings designed according to the Chinese and the US codes are systematically quantified and compared in the present study, using the FEMA P-58 procedure and the associated software PACT. Detailed quantifying analysis was conducted based on the three key features of a resilient system (i.e., reduced failure probabilities, reduced consequences from failures, and reduced time to recovery). The analysis results provide a quantitative comparison of the seismic resilience of the two buildings, and can be easily understood by the building owners and government authorities. To this end, the present study demonstrates an important scientific advancement to the traditional seismic performance evaluation. Overall, both buildings are found to exhibit similar seismic resilience, yet Building 2N performs slightly better in most seismic cases. Detailed conclusions are drawn as follows:

(1) Both Buildings 2A and 2N display sufficient collapse resistance and seismic safety. Building 2N performs slightly better in terms of the failure probabilities.

(2) At the three earthquake intensities, the repair costs of Building 2N are smaller than those of Building 2A. For both buildings, no casualty was observed at the SLE and DBE levels, and very few casualties were discovered at the MCE level.

(3) Building 2N requires less repair time at the SLE and DBE levels. This is mainly because of the larger stiffness and smaller inter-story drift and floor accelerations of Building 2N. However, Building 2N necessitates a longer repair time at the MCE level because more structural components of Building 2N are damaged.

(4) At the three earthquake intensities, the repair time and repair costs of the nonstructural components, such as HVAC, partitions and wall finishes, constitute the majority of the overall time and cost. When no building collapse occurs, the suspended ceilings and elevators may be the main cause of casualties. Thus, more attention must be paid to these nonstructural components in the design. Further, more reliable design methods and construction detailing for the nonstructural components are highly recommended to improve the seismic resilience of the whole structures.

Acknowledgement

The authors are grateful for the financial support received from the National Key Technology R&D Program (No. 2015BAK17B03).

Appendix A Fragility specifications for Buildings 2A and 2N

The fragility specifications of the structural components of Buildings 2A and 2N are provided in Table 3. The fragility specifications of nonstructural components for Buildings 2A and 2N are given in Table 4.

Table 3 Fragility specifications of structural components in Buildings 2A and 2N

Table 4 Nonstructural component fragility specifications used in PACT models

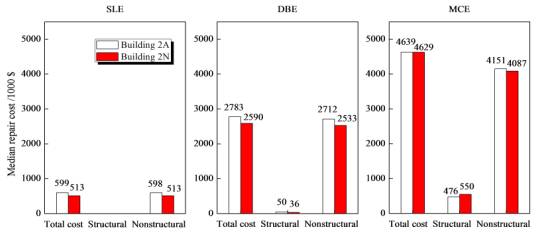
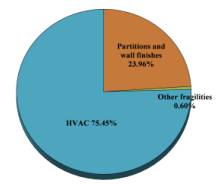
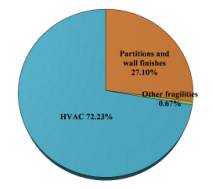
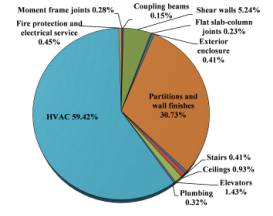
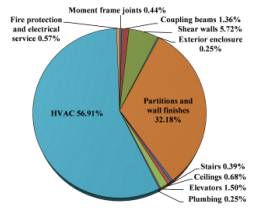
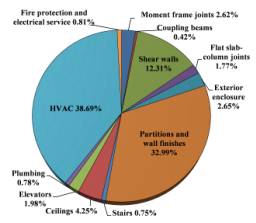
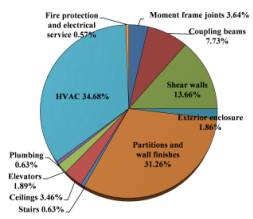
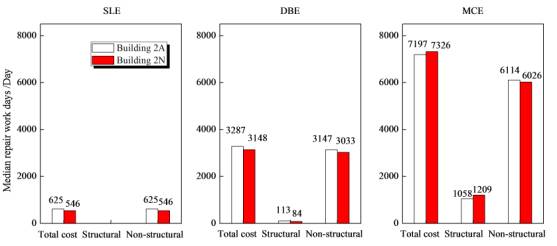
References

Almufti, I., Willford, M. (2013), ※REDi^TM Rating System: Resilience-based Earthquake Design Initiative for the Next Generation of Buildings§, ARUP Co.

Asgarian, B., Sadrinezhad, A. and Alanjari, P. (2010), ※Seismic performance evaluation of steel moment resisting frames through incremental dynamic analysis§, J. Constr. Steel Res., 66(2), 178-190.

Bazzurro, P. and Cornell, C.A. (1994a), ※Seismic hazard analysis of nonlinear structures. I: Methodology§, J. Struct. Eng., 120(11), 3320-3344.

Bazzurro, P. and Cornell, C.A. (1994b), ※Seismic hazard analysis of nonlinear structures. II: Applications§, J. Struct. Eng., 120(11), 3345-3365.

Bertero, V.V. (1977), ※Strength and deformation capacities of buildings under extreme environments§, Structural engineering and structural mechanics, 53(1), 29-79.

Biondini, F., Camnasio, E., and Titi, A. (2015), ※Seismic resilience of concrete structures under corrosion§, Earthq. Eng. Struct. D., 44(14), 2445-2466.

Bruneau, M., Chang, S.E., Eguchi, R.T., Lee, G.C., O＊Rourke, T.D., Reinhorn, A.M., Shinozuka, M., Tierney, K., Wallace, W.A., and von Winterfeldt, D. (2003), ※A framework to quantitatively assess and enhance the seismic resilience of communities§, Earthq. Spectra, 19(4), 733-752.

Chang, S.E., and Shinozuka, M. (2004), ※Measuring improvements in the disaster resilience of communities§, Earthq. Spectra, 20(3), 739-755.

Chang, C.M., Wang, Z.H., Spencer, Jr. B.F., and Chen, Z.Q. (2013), ※Semi-active damped outriggers for seismic protection of high-rise buildings§, Smart Struct. Syst., 11(5), 435-451.

Christovasilis, I.P., Filiatrault, A., Constantinou, M.C. and Wanitkorkul, A. (2009), ※Incremental dynamic analysis of woodframe buildings§, Earthq. Eng. Struct. D., 38(4), 477-496.

Cimellaro, G.P., Reinhorn, A.M., and Bruneau, M. (2010), ※Seismic resilience of a hospital system§, Struct. Infrastruct. E., 6(1-2), 127-144.

GB50011-2010. (2010), Code for Seismic Design of Buildings, Beijing, China (in Chinese)

Comerio, M.C. (2000), ※The economic benefits of a disaster resistant university: Earthquake loss estimation for UC Berkeley§, Institute of Urban & Regional Development, Berkeley, California, USA.

Comerio, M.C., and Blecher, H.E. (2010), ※Estimating downtime from data on residential buildings after the Northridge and Loma Prieta Earthquakes§, Earthq. Spectra, 26(4), 951-965.

Davis Langdon. (2010), ※Program cost model for PEER tall buildings study concrete dual system structural option§, Pacific Earthquake Engineering Research Center, Los Angeles, California, USA.

Dec辰, A., Bocchini, P., and Frangopol, D.M. (2013), ※A probabilistic approach for the prediction of seismic resilience of bridges§, Earthq. Eng. Struct. D., 42(10), 1469-1487.

Eads, L., Miranda, E., Krawinkler, H. and Lignos D.G. (2013), ※An efficient method for estimating the collapse risk of structures in seismic regions§, Earthq. Eng. Struct. D., 42(1), 25-41.

Fan, H., Li, Q.S., Tuan, A.Y., and Xu, L.H. (2009), ※Seismic analysis of the world＊s tallest building§, J. Constr. Steel Res., 65(5), 1206-1215.

FEMA. (2008), Casualty Consequence Function and Building Population Model Development (FEMA P-58/BD-3.7.8), Federal Emergency Management Agency; Washington, DC, USA.

FEMA. (2009), Quantification of building seismic performance factors (FEMA P695), Federal Emergency Management Agency; Washington, DC, USA.

FEMA. (2012a), Seismic Performance Assessment of Buildings: Volume 1 - Methodology (FEMA P-58-1), Federal Emergency Management Agency; Washington, DC, USA.

FEMA. (2012b), Seismic Performance Assessment of Buildings: Volume 2 - Implementation guide (FEMA P-58-2), Federal Emergency Management Agency; Washington, DC, USA.

He, M.J., Li, Z., Ma, R.L., and Liang, F. (2014), ※Experimental and numerical investigations on seismic performance of a super tall steel tower§, Earthquakes and Structures, 7(4), 571-586.

Hemsas, M., Elachachi, S.M., and Breysse, D. (2014), ※Seismic response and damage development analyses of an RC structural wall building using macro-element§, Struct. Eng. Mech., 51(3), 447-470.

Jacques, C.C., Mcintosh, J., Giovinazzi, S., Kirsch, T.D., Wilson, T., and Mitrani-Reise, J. (2014), ※Resilience of the Canterbury hospital system to the 2011 Christchurch Earthquake§, Earthq. Spectra, 30(1), 533-554.

Jiang, H.J., Fu, B., Liu, L.E., and Yin, X.W. (2014), ※Study on seismic performance of a super-tall steel-concrete hybrid structure§, Struct. Des. Tall Spec., 23(5), 334-349.

Kim, S., and Lee, K. (2013), ※Seismic Performance of Wind-Designed Diagrid Tall Steel Buildings in Regions of Moderate Seismicity and Strong Wind§, Steel Compos. Struct., 14(2), 155-171.

Kircher, C.A. (2003), ※It makes dollars and sense to improve nonstructural system performance§, Proceedings of ATC 29-2 Seminar on Seismic Design, Performance, and Retrofit of Nonstructural Components in Critical Facilities, Newport Beach, CA, USA, October 23-24.

Liu, X.J., and Jiang, H.J. (2013), ※Stake-of-the-art of performance-based seismic research on nonstructural components§, Journal of Earthquake Engineering and Engineering Vibration, 33(6), 53-62. (in Chinese)

Lu, X., Lu, X.Z., Zhang, W.K., and Ye, L.P. (2011), ※Collapse simulation of a super high-rise building subjected to extremely strong earthquakes§, Science China-Technological Sciences, 54(10), 2549-2560.

Lu, X., Lu, X.Z., Guan, H., and Ye, L.P. (2013b), ※Collapse simulation of reinforced concrete high-rise building induced by extreme earthquakes§, Earthq. Eng. Struct. D., 42(5), 705-723.

Lu, X., Lu, X.Z., Sezen, H., and Ye, L.P. (2014), ※Development of a simplified model and seismic energy dissipation in a super-tall building§, Eng. Struct., 67, 109-122.

Lu, X.L., Zou, Y., Lu, W.S., and Zhao, B. (2007), ※Shaking table model test on Shanghai World Financial Center Tower§, Earthq. Eng. Struct. D., 36(4), 439-457.

Lu, X.Z., Lu, X., Guan, H., Zhang, W.K., and Ye, L.P. (2013a), ※Earthquake-induced collapse simulation of a super-tall mega-braced frame-core tube building§, J. Constr. Steel Res., 82, 59每71.

Lu, X.Z., Xie, L.L., Guan, H., Huang, Y.L., and Lu, X. (2015a), ※A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees§, Finite Elem. Anal. Des., 98, 14-25.

Lu, X.Z., Li, M.K., Guan, H., Lu, X., and Ye, L.P. (2015b), ※A Comparative case study on seismic design of tall RC frame-core-tube structures in China and USA§, Struct. Des. Tall Spec., 24(9), 687-702.

Lu, X., Lu, X.Z., Guan, H., and Xie, L.L. (2016a), ※Application of earthquake-induced collapse analysis in design optimization of a super-tall building§, Struct. Des. Tall Spec., DOI: 10.1002/tal.1291.

Lu, X.Z., Xie, L.L., Yu, C., and Lu, X. (2016b), ※Development and application of a simplified model for the design of a super-tall mega-braced frame-core tube building§, Eng. Struct., 110, 116-126.

Mieler, M.W., Stojadinovic, B., Budnitz, R.J., Mahin, S.A., and Comerio, M.C. (2013), ※Toward resilient communities: A performance-based engineering framework for design and evaluation of the built environment§, Pacific Earthquake Engineering Research Center, University of California, Berkeley, California, USA, September.

Moehle, J., Bozorgnia, Y., Jayaram, N., Jones, P., Rahnama, M., Shome, N., Tuna, Z., Wallace, J., Yang, T., and Zareian, F. (2011), ※Case studies of the seismic performance of tall buildings designed by alternative means§, Pacific Earthquake Engineering Research Center, University of California, Berkeley, California, USA, July.

Nazri, F.M. and Ken, P.Y. (2014), ※Seismic performance of moment resisting steel frame subjected to earthquake excitations§, Front. Struct. Civ. Eng., 8(1), 19-25.

Poon, D., Hsiao, L., Zhu, Y., Joseph, L., Zuo, S., Fu, G. and Ihtiyar, O. (2011), ※Non-Linear Time History Analysis for the Performance Based Design of Shanghai Tower§, Structures Congress 2011, Las Vegas, Nevada, USA, April, 14-16.

PPD-8 (2011), Presidential Policy Directive/PPD-8: National Preparedness, http://www.dhs.gov/presidential-policy-directive-8-national-preparedness, the White House, Washington, DC, USA, March 20, 2011. [accessed 8 January 2016]

PPD-21 (2013). Presidential Policy Directive/PPD-21, http://www.whitehouse.gov/the-press-office/2013/02/12/presidential-policy-directive-critical-infrastructure-security-and-resil, the White House, Washington, DC, USA, February 12, 2013. [accessed 8 January 2016]

Rose, A. (2004), ※Defining and measuring economic resilience to disasters§, Disaster Prevention and Management, 13(4), 307每314.

Shi, W., Lu, X.Z., Guan, H. and Ye L.P. (2014), ※Development of seismic collapse capacity spectra and parametric study§, Adv. in Struct. Eng., 17(9), 1241-1256.

Takewaki, I., and Tsujimoto, H. (2011), ※Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands§, Earthquakes and Structures, 2(2), 171-187.

TBI. (2010), Guidelines for performance-based seismic design of tall buildings, Pacific Earthquake Engineering Research Center; Berkeley, California, USA.

United Nations Development Programme (2015), UNDP announces ＆5-10-50＊ 每 new global programme in support of disaster resilience, http://www.undp.org/content/undp/en/home/presscenter/pressreleases/2015/03/17/undp-announces-5-10-50-new-global-programme-in-support-of-disaster-resilience.html, UNDP, 17 March, 2015. [accessed 29 December 2015].

Vamvatsikos, D. and Cornell, C.A. (2002), ※Incremental dynamic analysis§, Earthq. Eng. Struct. D., 31(3), 491-514.

Wikipedia Contributors (2015), List of tallest buildings in Christchurch, https://en.wikipedia.org/w/index.php?title=List_of_tallest_buildings_in_Christchurch&oldid=675499611, Wikipedia, The Free Encyclopedia; 10 August 2015, 23:55 UTC. [accessed 23 August 2015]