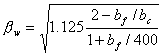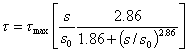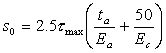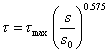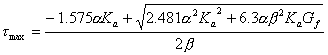FRP-混凝土界面行为研究/Studies on FRP-Concrete Interface
陆新征/Xin-zheng Lu
清华大学工学博士学位论文 / Tsinghua University Dissertation
2004
第二章 FRP-混凝土界面力学性能研究综述
2.1 引言
FRP-混凝土的界面粘结是保证两种材料共同工作的基础。试验表明,大量的FRP加固混凝土构件往往由于界面剥离而发生破坏 [8] ,因此正确的界面剥离强度模型和粘结-滑移模型,对建立FRP加固混凝土结构的设计计算理论至关重要。为此,各国学者都对该问题进行了大量的研究。
一般认为,在FRP加固混凝土结构中,FRP-混凝土界面的粘结应力主要为剪应力。例如,在受弯加固中,梁底部粘贴的FRP通过界面剪应力使FRP受拉,承担一部分截面弯矩,提高抗弯承载力;又如,在受剪加固中,梁侧面粘贴的FRP也是通过界面剪应力使FRP受拉来承担一部分剪力,并阻止斜裂缝的开展,提高构件的抗剪承载力。只有在少数情况下,FRP-混凝土界面之间的正应力才会有重要影响。例如,受弯加固时,在FRP端部由于FRP截断引起此处截面抗弯刚度突变,出现应力集中而导致剥离破坏的情况;又如,在斜裂缝两侧梁发生刚体错动,使梁底部的FRP-混凝土的界面产生正应力,从而会加剧FRP的剥离破坏。在实际工程应用中,由于可以通过布置FRP U型箍或机械锚固等方式来避免界面正应力的不利影响,因此FRP-混凝土界面力学性能的研究重点,主要集中在界面受剪性能以及由此导致的剥离破坏。
界面受剪性能一般可以用面内剪切试验加以研究。尽管不同的研究者采用的各种面内剪切试验方法 [23-33] 有所不同(见图2-1),但均可以统一到图2-2所示的基本力学模型 [34,35] :FRP条带粘贴在一混凝土长方体试块表面,在FRP上施加一个拉力,拉力位于FRP平面内,将FRP从混凝土块体上拉下来。根据试验现象,FRP-混凝土界面的受剪剥离破坏主要有以下5种破坏形式 [36] :
(1) FRP内部分层剥离破坏;
(2) FRP-胶层之间界面的剥离破坏;
(3) 胶层内部的剥离破坏;
(4) 胶层和混凝土之间的剥离破坏;
(5) 界面下混凝土开裂导致的剥离破坏。


(a) 双剪试验 [37] (b) 单剪试验 [38]
图 2-1 不同面内剪切试验方法
在上述5种破坏形式中,对于目前最常使用的有机胶层而言,由于胶层和纤维之间可以很好浸润,胶层的抗拉强度又远高于混凝土,故前4种破坏形式在胶层施工可靠的情况下一般不会出现,也是FRP加固混凝土所不容许出现的破坏形式,否则将视为材料和施工质量不合格。因此“理想可靠”的界面剥离破坏是胶层下混凝土被扯下一层,如图2-2中虚线所示,在界面下混凝土中出现一条和界面平行的裂缝,从加载端向自由端发展,并最终将整个FRP连同界面下2~5mm厚度的混凝土一起剥离下来。如果混凝土试块宽度大于FRP片材宽度,则剥离下来的混凝土将略宽于FRP(图2-2,2-3)。
FRP-混凝土界面受力性能的一个重要特点是存在一个有效锚固长度Le的概念 [23,24,32,39] ,即:如果FRP的粘结长度L小于Le,则剥离承载力会随着粘结长度的增加而提高;如果FRP的粘结长度大于Le,则继续增加粘结长度将不能继续提高剥离承载力。另外,如果试验中在加载端预留的非锚固长度不足,则加载端附近角部的混凝土往往也会被拉下来一块 [37,40] (图2-2,图2-3)。
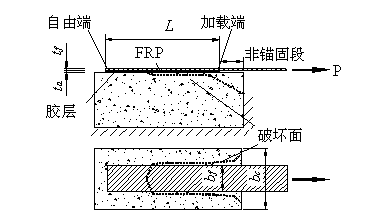
图2-2 面内剪切试验力学模型
(a) 双剪试验剥离破坏 [37] (b) 单剪试验剥离破坏 [38]
图2-3 剥离破坏试验照片
2.2 FRP-混凝土界面力学性能的试验研究
2.2.1 试验方案
做面内剪切试验时,应尽量使FRP与混凝土界面之间为纯剪力状态。根据现有各种面内剪切试验方案,本研究设计了一套试验卡具,如图2-4所示。本套卡具包含2个卡头,用来固定混凝土试块。每个卡头分为2个部分:卡头部分和施加荷载部分。卡头部分直接与混凝土试块接触,施加荷载部分加工为万向转铰,消除加载过程中偏心的影响,使试块两端FRP受力均匀。试验时,为防止混凝土局部受压破坏,在混凝土试块与卡具间垫入2mm厚,40mm宽的钢板。
图2-4 面内剪切试验夹具
面内剪切试验试件尺寸如图2-5a所示,试件上半部分为非量测区,为防止其破坏,延长粘结长度的同时,外加50mm宽的FRP布缠绕粘贴。混凝土立方体强度为37.6MPa,通过变化FRP的宽度bf、粘结长度L、预留长度a、FRP层数以及FRP类型等研究FRP布与混凝土之间的剥离性能。本试验共12个试块,FRP的力学性能如表2-1所示,各试块参数以及试验结果如表2-2所示。应变片分布方式为:从距离FRP加载端5mm开始,每隔10mm粘贴一个应变片,最后2个应变片间距离为15mm,见图2-5b。
(a)
(b)
图2-5 面内剪切试验试块及应变量测
表2-1 FRP力学性能
|
GFRP厂家检测数据 |
GFRP实际测得数据 |
CFRP厂家检测数据 |
|||
|
拉伸强度MPa |
弹性模量GPa |
拉伸强度MPa |
弹性模量GPa |
拉伸强度MPa |
弹性模量GPa |
|
2801.5 |
102.1 |
2777 |
97.0 |
3500 |
235 |
注:CFRP材性数据采用厂家提供数据,GFRP材性数据使用实际测得数据。
表2-2试件参数及主要试验结果
|
编号 |
FRP参数 |
极限荷载 Pu/2 (kN) |
|||||
|
类型 |
厚度(mm) |
宽度 (mm) |
粘结长度(mm) |
弹性模量(GPa) |
极限强度(MPa) |
||
|
T-1 |
GFRP |
0.169 |
50 |
130 |
97 |
2777 |
7.78 |
|
T-2 |
9.19 |
||||||
|
T-3 |
75 |
10.11 |
|||||
|
T-4 |
13.95 |
||||||
|
T-5 |
50 |
100 |
6.87 |
||||
|
T-5a |
9.20 |
||||||
|
T-6 |
70 |
6.46 |
|||||
|
T-6a |
6.66 |
||||||
|
T-7 |
0.338 |
130 |
10.49 |
||||
|
T-8 |
11.43 |
||||||
|
T-9 |
CFRP |
0.111 |
235 |
3500 |
7.97 |
||
|
T-10 |
9.19 |
||||||
注: tf为FRP厚度;Ef为FRP弹性模量;bf为FRP宽度。
2.2.2 试验结果
试验得到的剥离破坏形式可以分为两大类:(1)剥离发生在粘结树脂层和(2)剥离发生在混凝土层。T-5a和T-6a试块为数值层剥离破坏形式(图2-6a),其剥离下来的FRP表面平整,没有粘下混凝土(或者仅零星粘有几小片混凝土),出现这种剥离破坏的原因是粘结树脂的粘结作用不足。这种剥离破坏属于“不成功”剥离。其他试块为混凝土层剥离破坏,其剥离下来的FRP表面粘有2~5mm厚的混凝土,见(图2-6b),部分试块剥离下来的FRP将混凝土边缘拉下15mm×15mm的三角柱状混凝土(图2-6c),说明粘结情况良好,均属于“成功”剥离。
(a) T-5a树脂层破坏 (b) T-1混凝土层破坏
(c) 混凝土层破坏,试块角部被拉坏
图2-6 试验破坏形式
试验得到的典型试件FRP应变分布发展如图2-7所示,图中,s(mm)为加载端滑移量;P(kN)为荷载;Pu(kN)为剥离承载力。从图中可以看出,在加载早期,只有加载端附近FRP承受荷载,随着荷载的增大,参与受力的FRP长度增加。当参与受力的FRP长度达到有效锚固长度Le后,荷载不再增加,剥离从加载端向自由端发展。
(a) T-8 (b) T-10
图2-7 典型试件FRP应变发展
2.2.3 其他试验研究
各国学者对FRP-混凝土界面的受力性能进行了大量的试验研究。尽管各个研究者的试验方法各有不同,但各种试验方法之间结果的差别并不显著
[34,35] 。从现有文献中 [24,37,38,41-47] ,共收集到254个面内剪切试验记录,这些试验记录提供了FRP厚度 ![]() ,宽度
,宽度 ![]() ,粘结长度
,粘结长度 ![]() ,弹性模量
,弹性模量 ![]() ,极限强度
,极限强度 ![]() ,以及混凝土立方体抗压强度
,以及混凝土立方体抗压强度 ![]() 和宽度
和宽度 ![]() 等重要参数,现将它们列于附录A。另外,有些文献还提供了FRP的应变分布。
等重要参数,现将它们列于附录A。另外,有些文献还提供了FRP的应变分布。
这些试件的4个主要影响参数的分布情况如图2-8所示,可见这些试件覆盖了一个较广的参数范围,基于这些试验结果可以对各种界面模型进行比较全面的评价。
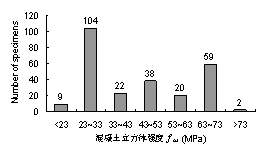
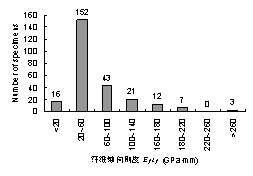
(a) 混凝土立方体强度分布 (b) FRP纤维轴向刚度分布
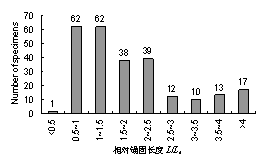
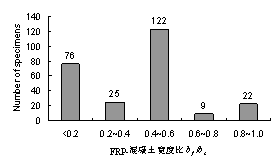
(c) 粘结长度分布 (d) FRP-混凝土宽度比分布
注: Le为Chen & Teng [36] 建议的有效锚固长度
图2-8 试验数据的主要影响参数分布
2.3 FRP-混凝土界面数值模拟研究
除去试验方法外,数值分析,尤其是有限元分析,也是目前研究者对FRP-混凝土界面受力性能进行研究最常用的分析方法。早期的界面有限元分析研究多是基于线弹性分析,主要是希望了解FRP-混凝土界面的应力集中状况 [34,48] ,相关的研究在解决由界面应力集中引起的FRP受弯加固RC梁端部剥离问题中发挥了比较重要的作用 [48-53] 。但是,由于线弹性数值分析无法反映混凝土的非线性力学性能,因而无法模拟界面的剥离破坏过程,也就难以解释界面的剥离破坏机理。所以近年来对FRP-混凝土界面力学性能的研究转向非线性分析,这些分析可分为两类:
(1) 一类是在FRP和混凝土单元之间引入专门的界面单元 [54-57] ,并预先设定合适的界面单元的粘结-滑移本构关系,通过界面单元的失效来模拟界面剥离破坏的过程。这种研究方法的好处是,只要界面单元粘结-滑移行为设置得合适,就可以很方便的模拟界面的剥离破坏,有限元分析的技术难度较小。但是,由于目前对FRP-混凝土界面粘结-滑移本构行为本身还没有很深入的认识,难以确认本构模型的合理性。因此,在设置界面单元粘结-滑移本构时往往有着很大的随意性,计算结果也因粘结-滑移关系不同而差异显著。另外,由于剥离破坏被假设在界面单元内,因而也就无法从实质上研究界面剥离破坏的机理。
(2) 另一类研究方法是将FRP和混凝土单元通过共用节点直接联系在一起 [57-60] ,并选取适当的混凝土本构模型,用界面下混凝土单元的断裂破坏来模拟FRP-混凝土界面的剥离过程。由前述试验研究可知,对于“理想可靠”的粘结,剥离破坏均应发生在FRP下的混凝土层中,因此这种将界面剥离问题和混凝土本构关系联系在一起的分析方法,理论上说,对深入研究界面剥离破坏机理及其相应的影响参数更为合理,并可通过数值分析直接获得界面粘结性能本构模型。可是,这种方法虽然概念上非常简单,理论上也合理,但由于混凝土非线性分析的复杂性,尤其是剥离破坏仅发生的2~5mm厚的混凝土层中,因而在具体实现中还很多困难,本文将在后续章节中详细介绍。
2.4 FRP-混凝土界面的剥离承载力
2.4.1影响参数
根据试验研究,以及本文后面的数值模拟和理论分析,影响界面粘结性能和剥离承载力的主要影响参数有以下6个:
(1) 混凝土强度
由于剥离破坏发生在界面以下的混凝土中,因而混凝土强度对界面粘结性能和剥离承载力影响显著。很多研究者都指出界面破坏能主要与混凝土强度有关 [9,45,61,62] 。
(2) 粘结长度
FRP片材粘贴长度是影响极限剥离承载力的重要因素。如前所述,在粘结长度小于有效锚固长度Le时,剥离承载力随粘结长度增加而提高。
(3) FRP片材刚度
试验研究表明,FRP片材的刚度越大,可以使界面粘结应力更加均匀,增大有效锚固长度Le,并可减弱加载端附近粘结应力集中。
(4) 宽度比
如图2-2,2-3所示,很多试验观测发现剥离下来的混凝土比FRP片材要宽一些,因此参与界面受剪的混凝土宽度要大于FRP片材的宽度,且剥离承载力随宽度比bc/bf(bc为混凝土块体宽度,bf为FRP片材宽度,见图2-2)的增加而有所提高,但不会随宽度比bc/bf的增加而无限提高,存在一个宽度影响的上限。
(5) 胶层
在面内剪切试验中,拉力直接作用在FRP片材上,所以FRP和混凝土之间的胶层接近于纯剪应力状态(图2-2)。由于普通有机胶层的抗拉强度远高于混凝土的抗拉强度,所以普通胶层对界面粘结性能的影响很小。虽然有研究表明 [61] ,非常软的胶层(剪切刚度是普通胶层的1/20~1/5)可以提高界面的剥离承载力,但是这方面的试验研究还很少,本文暂不讨论。
(6) 位置以及端部约束
如图2-2,2-3所示,如果加载端的非粘结段长度不足,则剥离破坏时角部的混凝土块体将被拉下来。理论分析表明[65],在角部区域的粘结强度比其他部位的要小。不过,在面内剪切试验中,当粘结长度超过一定值后,角部局部的粘结-滑移行为不会对最终剥离承载力产生较大影响。
2.4.2 界面剥离承载力模型
由面内剪切试验比较容易获得剥离承载力,因此自1996年来,国内外基于粘贴FRP片材或钢板的面内剪切试验结果提出了很多界面剥离承载力公式。根据文献调研,共收集到12个界面剥离承载力模型,现逐一介绍如下:
(1) Hiroyuki & Wu 模型 [31]
|
|
(2.1a) |
|
|
|
(2.1b) |
式中, ![]() (MPa)为平均粘结应力;
(MPa)为平均粘结应力; ![]() (mm)为粘结长度;
(mm)为粘结长度; ![]() 为界面剥离承载力。
为界面剥离承载力。
(2) Tanaka模型 [63]
|
|
(2.2a) |
|
|
|
(2.2b) |
(3) Gemert模型 [27,30]
|
|
(2.3) |
式中,ft(MPa)为混凝土抗拉强度。
(4) Chaallal et al. 模型 [64]
|
|
(2.4a) |
|
|
|
(2.4b) |
式中,Ea为胶层的弹性模量;ba为胶层宽度;If为FRP的惯性矩;ta为胶层厚度。
(5) Maeda et al. 模型 [32]
|
|
(2.5a) |
|
|
|
(2.5b) |
|
|
if |
(2.5c) |
|
|
|
(2.5d) |
(6) K. Izumo 模型 [65]
对碳纤维
|
|
(2.6a) |
对芳纶纤维
|
|
(2.6b) |
式中,fc(MPa)为混凝土抗压强度。
(7) Sato 模型 [65]
|
|
(2.7a) |
|
|
|
(2.7b) |
|
|
if |
(2.7c) |
|
|
|
(2.7d) |
式中, ![]() mm,是混凝土参与工作宽度。
mm,是混凝土参与工作宽度。
(8) M. Iso 模型 [65]
|
|
(2.8a) |
|
|
|
(2.8b) |
|
|
if |
(2.8c) |
|
|
|
(2.8d) |
(9) Neubauer & Rostasy 模型 [33]
|
|
(2.9a) |
|
|
|
(2.9b) |
|
|
|
(2.9c) |
|
|
|
(2.9d) |
式中,bc(mm)为混凝土块体宽度,βw为宽度系数。
(10) Khalifa 模型 [66]
|
|
(2.10a) |
|
|
|
(2.10b) |
|
|
if |
(2.10c) |
|
|
|
(2.10d) |
式中,fc’ (MPa)为混凝土圆柱体抗压强度。
(11) 杨勇新等模型 [67]
|
|
(2.11a) |
|
|
|
(2.11b) |
|
|
|
(2.11c) |
(12) Chen & Teng 模型 [36]
|
|
(2.12a) |
|
|
|
(2.12b) |
|
|
|
(2.12c) |
|
|
|
(2.12d) |
|
|
|
(2.12e) |
2.4.3不同剥离承载力模型对关键影响因素的考虑对比
上述12个剥离承载力模型对2.4.1节中提到的前4个关键影响因素考虑程度的对比见表2-3。由表可见,早期模型考虑的影响因素都比较少,而近期的模型对各影响因素的考虑相对比较全面一些。尤其是有效锚固长度Le,在近期的模型中大多都考虑了。
表2-3 不同强度模型对关键因素的考虑
|
模 型 |
混凝土强度 |
FRP片材刚度 |
有效锚固长度 |
宽度比 |
|
|
1 |
Tanaka [63] |
No |
No |
No |
No |
|
2 |
Hiroyuki & Wu [31] |
No |
No |
No |
No |
|
3 |
van Gemert [27,30] |
Yes |
No |
No |
No |
|
4 |
Maeda et al [32] |
Yes |
Yes |
Yes |
No |
|
5 |
Neubauer & Rostasy [33] |
Yes |
Yes |
Yes |
Yes |
|
6 |
Khalifa et al. [66] |
Yes |
Yes |
Yes |
No |
|
7 |
No |
Yes |
No |
No |
|
|
8 |
Yes |
Yes |
Yes |
Yes |
|
|
9 |
Izumo [65] |
Yes |
Yes |
No |
No |
|
10 |
Sato [65] |
Yes |
Yes |
Yes |
No |
|
11 |
Iso [65] |
Yes |
Yes |
Yes |
No |
|
12 |
Yes |
Yes |
Yes |
No |
2.5 FRP-混凝土界面粘结性能本构模型
2.5.1 概述
面内剪切试验不仅被用来测定FRP-混凝土界面的剥离承载力,同时也被用来测定界面的局部粘结-滑移本构关系 [32,35,45,46,61,62,68,69] 。由面内剪切试验,界面粘结-滑移本构关系一般通过以下两种方法获得:
(1) 在FRP上布置应变片,量测FRP内的轴向应变分布ef,而后通过以下差分方程可以得到相应的局部粘结应力t:
|
|
(2.13a) |
同样局部滑移s可以通过对FRP应变从自由段开始按下式积分得到:
|
|
(2.13b) |
这方法虽然从理论上说非常简单,但是在实际分析中却遇到很多困难。首先,由于应变片标距的限制,应变测点不可能布置得非常密,因而由差分def/dx得到的界面粘结应力的误差也就相对较大。更重要的是,由于界面下混凝土中裂缝和材料组分的随机分布,对实测FRP应变有很大影响。例如,如果应变片下正好出现界面剥离裂缝,则此处测得的应变将远大于临近位置的FRP应变;而如应变片正好贴在一块骨料上方,则此处的应变又将远小于临近位置的应变。因此,很多研究者发现,即便参数完全一样,不同试件测得的局部粘结-滑移关系也会有很大差异 [45,62] 。因此,现阶段通过量测FRP应变分布还很难获得可靠的界面局部粘结-滑移关系。
(2) 通过加载端的荷载-滑移曲线推算出界面的粘结-滑移关系(例如文献 [62] )。但是,进一步的研究发现,荷载位移曲线对粘结-滑移关系并不是非常敏感,不同的局部粘结-滑移关系可以得到相似的荷载滑移曲线。
因此,目前用试验方法获得FRP-混凝土的界面粘结-滑移关系还存在很多困难。
根据Taljsten [23] 基于非线性断裂力学的研究,在FRP锚固长度足够大的情况下,界面剥离承载力由下式给出:
|
|
(2.14) |
式中, ![]() 为界面破坏能,它等于粘结-滑移曲线所包围的面积(图2-9)。由于该公式和粘结-滑移曲线形状无关,因此它对理解界面剥离行为的一些影响参数很有帮助。
为界面破坏能,它等于粘结-滑移曲线所包围的面积(图2-9)。由于该公式和粘结-滑移曲线形状无关,因此它对理解界面剥离行为的一些影响参数很有帮助。
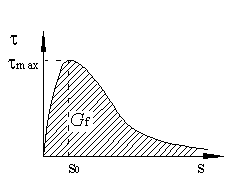
图 2-9 界面破坏能 ![]()
2.5.2 现有的本构模型
尽管通过面内剪切试验直接获得界面粘结-滑移本构关系非常困难,一些研究者还是提出了一些界面粘结-滑移本构关系。在现有文献中,共收集到6个界面粘结-滑移本构关系。另有一些试验者虽然给出了粘结-滑移本构关系,但没有给出其中参数的确定方法,因而无法进行分析对比,故这里不再列出。下面分别介绍这6个模型:
(1) Neubauer & Rostasy 模型 [9]
该模型为线性模型,粘结应力随滑移增加而线性上升,至剥离强度tmax后突然降低到零。这个模型在FRP-混凝土界面研究早期被广泛采用,Neubauer & Rostasy通过70个面内剪切试验结果回归给出了该模型中的参数,其表达式如下:
|
|
|
(2.15a) |
|
|
||
|
|
(2.15b) |
|
|
|
(2.15c) |
|
|
|
(2.15d) |
式中, ![]() (MPa)和
(MPa)和 ![]() (mm) 为局部粘结应力及滑移;
(mm) 为局部粘结应力及滑移; ![]() 为最大粘结应力,称为局部粘结强度;
为最大粘结应力,称为局部粘结强度; ![]() 为
为 ![]() 对应的滑移量(图2-9);
对应的滑移量(图2-9); ![]() 为宽度修正系数。
为宽度修正系数。
(2) Nakaba et al. 模型 [45]
Nakaba等人进行了30个面内剪切试验研究,并测量了FRP的应变分布情况,进而由FRP应变分布给出界面的粘结-滑移本构关系。该模型的公式为:
|
|
(2.16a) |
|
|
|
(2.16b) |
|
|
|
(2.16c) |
由于该模型基于实测FRP应变,因此从曲线形状上来说,该本构模型是最接近实际情况的。但如前所述,由于根据FRP应变分布确定界面粘结-滑移关系的方法会导致很大误差,因此在Nakaba等的试验中不同试件之间离散也很大,从后面的比较也可以看出,该模型给出的界面破坏能 ![]() 偏大,过高估计了界面的剥离承载力。
偏大,过高估计了界面的剥离承载力。
(3) Savioa et al. 模型 [70]
Savioa等人在Nakaba的工作基础上,用他们的试验结果对Nakaba模型中的参数进行了修正,最后得到的粘结-滑移模型为:
|
|
(2.17a) |
|
|
|
(2.17b) |
|
|
|
(2.17c) |
(4) Monti et al. 模型 [71]
Monti等首先假设界面粘结-滑移关系为双线性模型,这一简化模型在分析FRP-混凝土界面行为中也被广为采用,特别是由该模型可直接得到界面剥离承载力的解析解 [35] ,因而对于工程设计非常有用。Monti通过试验得到模型中的参数,最后给出的公式为:
|
|
|
(2.18a) |
|
|
(2.18b) |
|
|
|
(2.18c) |
|
|
|
(2.18d) |
|
|
|
(2.18e) |
|
|
|
(2.18f) |
|
|
|
(2.18g) |
式中,sf(mm)为粘结应力降低到零时对应的滑移量。
(5) Dai & Ueda 模型 [61]
Dai & Ueda用很软的胶层将FRP和混凝土粘结在一起,并发现这样可以提高界面的剥离承载力,根据29个胶层刚度Ka(Ka=Ga/ta,Ga为胶层剪切模量)在0.14~1.1GPa/mm的面内剪切试验结果,Dai & Ueda给出的界面粘结-滑移本构关系为:
|
|
|
(2.19a) |
|
|
(2.19b) |
|
|
|
(2.19c) |
|
|
|
(2.19d) |
|
|
|
(2.19e) |
|
|
|
(2.19f) |
|
|
|
(2.19g) |
|
|
|
(2.19h) |
(6) Ueda et al. 模型 [62]
基于同样一批试件,Ueda等人又提出了另一个界面粘结-滑移本构关系,该模型的公式为:
|
|
(2.20a) |
|
|
|
(2.20b) |
|
|
|
(2.20c) |
图2-10a为Neubauer模型,Savioa模型,Nakaba模型和Monti模型的粘结-滑移本构关系曲线对比,可见这四个模型的 ![]() 都差不多,Monti的模型可以看作是Nakaba模型的一个简化,而Neubauer模型则相对过于简化;图2-10b为Nakaba模型和Dai &
Ueda模型及Ueda et al.模型的粘结-滑移关系曲线对比,后两个模型由于是基于非常软胶层(
都差不多,Monti的模型可以看作是Nakaba模型的一个简化,而Neubauer模型则相对过于简化;图2-10b为Nakaba模型和Dai &
Ueda模型及Ueda et al.模型的粘结-滑移关系曲线对比,后两个模型由于是基于非常软胶层( ![]() )的试验结果,对于普通胶层(
)的试验结果,对于普通胶层( ![]() )时给出的粘结强度明显偏大过多。
)时给出的粘结强度明显偏大过多。
(a) Neubauer & Rostasy [9] , Nakaba et al. [45] Savioa et al. [70] , 和Monti et al. [71] 建议的粘结-滑移模型对比
(b) Dai & Ueda [61] , Ueda et al. [62] 和Nakaba et al. [45] 建议的粘结-滑移模型对比
图2-10 不同粘结-滑移模型对比
2.6 小结
本章对FRP-混凝土界面力学性能的研究现状进行了一个比较全面的回顾,对现有的试验结果、分析方法、剥离承载力模型以及粘结-滑移本构模型等资料都进行了全面的收集和整理。尤其是收集了不同研究者所完成的大量的面内剪切试验资料,这些资料所覆盖的参数范围较大,对本文进行深入的研究提供了可靠的试验依据。
尽管有不少研究者分别对剥离承载力和界面粘结-滑移本构关系提出了不同的模型,但这些现阶段研究存在着以下问题:
(1) 虽然进行了大量的试验研究,但是对剥离破坏的内在机理认识得还很不够,也无法提出可以真实再现剥离破坏过程的数值模型;
(2) 虽然已经提出了很多剥离承载力模型,但这些承载力模型主要是基于试验结果回归,缺少理论依据,不能保证其合理性;
(3) 试验量测界面粘结-滑移关系非常困难,且结果离散度很大,测得的粘结-滑移模型的准确性存在疑问;
(4) 与试验结果对比表明,现有粘结-滑移模型计算结果和试验之间存在较大差异(详细比较参见第五章);
因此,有必要提出一个可靠的模拟FRP-混凝土界面剥离问题的有限元模型,并基于有限元模型对界面剥离破坏机理进行探讨,提出能够正确反映界面行为的粘结-滑移本构模型。
|
目 录 |
I |
|
I |
|
|
1 |
|
5 |
|
25 |
|
41 |
|
59 |
|
80 |
|
94 |
|
134 |
|
150 |
|
178 |
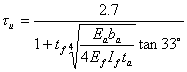
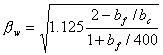

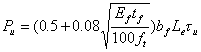

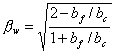
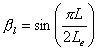 if
if
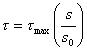 if
if