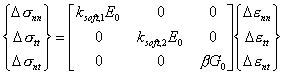FRP-混凝土界面行为研究/Studies on FRP-Concrete Interface
陆新征/Xin-zheng Lu
清华大学工学博士学位论文 / Tsinghua University Dissertation
2004
第四章 基于精细单元的界面力学性能的数值模拟
4.1 宏观单元模型的主要缺点
第三章中通过引入非共轴转动裂缝模型,并与试验结果比较标定其裂面参数,提出了基于宏观单元的有限元模型,对FRP-混凝土界面的力学行为和剥离问题进行了较好的模拟。相对于现有的FRP-混凝土界面剥离有限元分析工作而言 [56] ,该模型取得了较大的进展。但是,基于宏观模型的有限元分析有以下一些缺点:
(1) 模型中的裂面参数很多,且物理意义不够明确,也很难通过适当的材性试验获得;
(2) 虽然通过宏观模型基本掌握了界面剥离机理,但同时也由该模型的分析结果和试验观测得知,剥离发生在混凝土层厚度2~5mm以内,这个尺度与宏观单元模型的单元尺寸(2mm) 差不多,剥离裂缝的开展基本都是位于界面以下2~3层单元内,因此宏观模型难于获得界面裂缝的发生和发展过程,以及界面裂缝间的相互作用问题;
(3) 由宏观单元模型得到的粘结-滑移关系不稳定。
基于宏观模型对剥离破坏的认识,并针对其存在的问题,为进一步深入细致全面地了解和掌握FRP-混凝土界面的力学行为和剥离问题,本章提出一个基于精细单元的有限元模型,来更好地分析界面剥离问题。
固定裂缝模型(FACM)假设裂缝方向在开裂后就不再变化,这样可以比较容易地通过裂面剪切试验 [80] 来确定其裂面受剪行为。但是,在单元尺寸不是足够小的情况下,正交裂缝的固定裂缝模型无法模拟在剪力作用下裂缝角度的逐步变化(图3-6),这样就会在裂面上积累很高的剪应力,从而因剪应力锁死问题而带来的误差就会很大。但是,如果单元尺寸足够小,单元数量足够的多,有足够的单元来描述裂缝的发生、发展以及在剪应力作用下混凝土裂缝方向转动过程,则剪应力锁死问题就可以得到较好的解决,且可以更真实地跟踪整个破坏过程。另外,由于每个单元的裂缝模型都是固定裂缝模型,就可以使用现有的裂面剪切试验结果来描述其裂面行为,使裂缝模型参数的物理意义更加明确,这也就是提出精细单元模型的目的所在。当然,精细单元模型的一个主要问题就是计算量很大。但是,随着计算机能力的不断发展,这个问题将逐步得到解决。而其理论简单,参数明确的优点将会得到更多的应用。
本章使用的精细单元模型有以下特点:
(1) 混凝土单元尺寸比界面剥离下来的混凝土(一般2~5mm)小一个数量级(为0.25~0.5mm)。这样,在模拟剥离过程时,可以有足够的单元来模拟界面下裂缝的发生和扩展。从而比宏观裂缝模型更好地分析和解释界面破坏的内在机理;
(2) 精细单元混凝土裂缝模型基于常用的正交固定裂缝模型,其模型参数可以通过裂面剪切试验得到,物理意义更加明确;
(3) 精细单元模型对混凝土的本构模型的要求比宏观单元模型要简单得多,可以直接使用现有通用有限元程序中提供的混凝土本构模型,降低分析难度;
(4) 精细单元模型界面剥离破坏的过程更加稳定,便于根据有限元模型提出相应的界面粘结-滑移本构模型。
4.2 精细单元有限元模型
4.2.1 概述
如前所述,精细模型使用的混凝土单元尺寸非常小,为0.25~0.5mm,为减小计算工作量,将面内剪切试件简化为平面应力问题,并仍使用Chen & Teng [36] 建议的宽度修正系数(式3.4)来考虑FRP宽度和混凝土宽度差异的影响。
分析的有限元模型计算简图如图4-1所示。由于分析使用的单元尺寸很小,因此FRP和混凝土都可以使用平面四节点单元加以模拟。通过位移控制加载,以得到有限元分析的软化段。另外,有些面内剪切试件在加载端前面没有预留非粘结段,在试验中加载端前面的混凝土往往会被拉下来一个角,这会给有限元计算的收敛带来很大的问题,因此在本文的研究中,均在有限元模型的加载端前面都预留了一个25mm的非粘结段。这虽然和某些试验实际情况略有差异,但这个非粘结段的影响主要位于加载端附近,影响范围不大,且对剥离承载力也基本没有影响。
图4-1 精细单元有限元模型
4.2.2 FRP片材模型
如果加固的FRP片材属于预制成型的板材,则FRP和混凝土之间的胶层与FRP片材之间可以清晰区分。但是,对于更常见的湿作业粘贴FRP布,则胶层和纤维之间很难清晰加以区分 [8] 。由于精细模型的单元尺度很小,可以用不同单元来区分FRP和胶层,因此本文采用以下三种方式来分别模拟FRP片材(图4-2):
(a) 使用FRP的名义厚度和弹性模量建立有限元模型,不区分纤维和胶层,相当于不考虑胶层作用;
(b) 使用FRP的实际厚度和等效的弹性模量建立有限元模型,也不区分纤维和胶层,相当于将纤维均布在整个片材内;
(c) 使用FRP的实际厚度建立有限元模型,认为纤维分布在片材中心,其厚度是纤维的名义厚度,其余部分是胶层。
分析时将荷载同时施加在胶层和纤维上。通过对比以上三种情况的分析结果,发现相互之间差异很小(图4-3),这主要是由于剥离发生混凝土层中,与FRP的模型关系不大。同时计算分析表明,采用第二种方式建模,非线性收敛性较好,且建模简单,因此在后续分析中均使用第二种方式。湿作业的FRP片材厚度在不同试验中有所差异,本文中使用其平均厚度,即每层纤维1mm。


(a) FRP Model A (b) FRP Model B
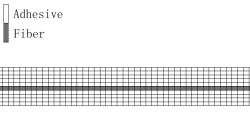
(c) FRP Model C
图4-2 不同的FRP有限元模型
图 4-3 不同FRP有限元计算模型对比
4.2.3 混凝土模型
由于本次分析中使用的混凝土单元非常小,比混凝土的骨料粒径还要小很多,因此真正的细观或微观力学模型需要考虑混凝土中骨料和水泥浆体之间的差异,以及二者之间的相互作用 [81-83] 。但是,本章使用的精细单元模型并没有考虑这一问题,这主要基于以下两点考虑:
(1) 本文分析的平面模型是实际空间三维试件进行平均化后的结果,也就是说,这个平面模型不是一个截面的行为,而是一个三维空间试件的整体平均行为,故可以把混凝土视为均匀材料 [22] ;
(2) 本文使用微小单元的目的是为了跟踪剥离破坏中裂缝的发展过程,对骨料与水泥浆间的差异并不是关心的重点,因此本章研究中的混凝土材料模型仍然采用均匀材料模型。
由于混凝土单元尺寸非常小,因此单元尺寸效应不可忽略,特别是使用最大拉应力准则作为开裂判据时,损伤局部化会严重降低构件的强度。因此,需要对混凝土的本构模型加以调整,以考虑尺寸效应的影响。
4.2.3.1 混凝土受压行为
本次分析认为混凝土受压行为与单元尺寸关系不大 [22, 81] ,混凝土受压行为可以直接使用通用有限元程序MSC.MARC [73] 提供的混凝土本构模型,而不必像宏观单元模型那样专门设定其受压本构关系。
MSC.MARC程序中混凝土的本构模型为弹塑性模型,采用Buyukozutrk [84] 建议的屈服面模型,由下式给出:
|
|
(4.1) |
式中,f为屈服面;I1为第一应力不变量;J2为第二偏应力不变量;
![]() 为等效应力;
为等效应力; ![]() 和
和 ![]() 为系数,Buyukozuturk [84] 建议
为系数,Buyukozuturk [84] 建议 ![]() 。
。
混凝土的受压等效单轴应力应变曲线采用的是Hognestad [85] 建议的模型:
|
|
|
(4.2a) |
|
|
(4.2b) |
式中, ![]() ;
; ![]() ;
; ![]() ;
; ![]() (MPa)为混凝土抗压强度。
(MPa)为混凝土抗压强度。
4.2.3.2 混凝土受拉行为
由于精细单元模型使用的是最常用的固定正交裂缝模型,因此可以直接使用MSC.MARC程序中提供的混凝土裂缝模型,只需对该裂缝模型的参数加以适当调整,以考虑单元尺寸效应的影响。
由于混凝土受拉开裂和单元尺寸大小关系明显,因此本文采用Bazant等 [86,87] 提出的裂缝带模型(Crack band model)来考虑混凝土的单元尺寸效应。在有限元分析中,对于平面应力问题,当混凝土单元的一个高斯点上出现两条裂缝时,在开裂方向其增量形式的应力应变关系为:
|
|
(4.3) |
式中, ![]() 和
和
![]() 为裂缝1方向的正应力和正应变;
为裂缝1方向的正应力和正应变;
![]() 和
和
![]() 为裂缝2方向的正应力和正应变;
为裂缝2方向的正应力和正应变;
![]() 和
和
![]() 为剪应变和剪应力;
为剪应变和剪应力;
![]() 和
和
![]() 为混凝土的初始弹性模量和剪切模量;
为混凝土的初始弹性模量和剪切模量;
![]() 和
和
![]() 为裂缝1、2方向的混凝土开裂受拉软化系数;
为裂缝1、2方向的混凝土开裂受拉软化系数;
![]() 为剪力传递系数,反映裂缝表面混凝土之间的相互咬合作用。
为剪力传递系数,反映裂缝表面混凝土之间的相互咬合作用。
根据Kwak & Filipppou [88] 的研究,当单元尺寸小于三倍最大骨料粒径时,开裂应变可以视作是在单元内均匀分布的。这时,混凝土的断裂能可以写作:
|
|
(4.4) |
式中, ![]() 为裂缝带宽度,它等于在裂缝张开方向的单元长度,和混凝土断裂力学的结论一致。而第三章宏观单元模型认为裂缝带宽度为60mm是没有依据的。
为裂缝带宽度,它等于在裂缝张开方向的单元长度,和混凝土断裂力学的结论一致。而第三章宏观单元模型认为裂缝带宽度为60mm是没有依据的。
为了比较不同混凝土软化模型的影响,本文使用了两种应用最为广泛的混凝土受拉软化模型来进行对比分析:一个为线性软化模型(图4-4a);另一个为双线性软化模型 [89] (图4-4b)。根据欧洲模式规范MC90 [78] ,混凝土的断裂能为:
|
|
(4.5) |
式中, ![]() (MPa)为混凝土抗压强度。对于普通粒径混凝土,
(MPa)为混凝土抗压强度。对于普通粒径混凝土, ![]() 。因此,当混凝土的受拉软化曲线、抗压强度、抗拉强度以及单元尺寸确定后,考虑单元尺寸的受拉软化应力应变曲线也就可以确定了。
。因此,当混凝土的受拉软化曲线、抗压强度、抗拉强度以及单元尺寸确定后,考虑单元尺寸的受拉软化应力应变曲线也就可以确定了。
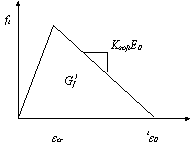
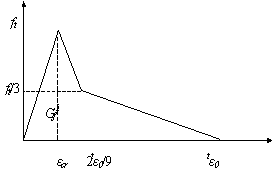
(a) 线性断裂软化模型 (b) 双线性断裂软化模型
图4-4 开裂受拉软化模型
4.2.3.3 开裂混凝土的剪切行为
开裂混凝土的裂面剪切行为同样对计算结果影响显著,且与单元尺寸大小关系密切。常用的恒定剪力传递系数模型显然不再适用,因此本文选取了5个不同的裂面剪力模型,并对它们的计算结果进行了比较。这5个裂面剪力模型分别为:
(1) 恒定剪力传递系数模型
|
|
(4.6a) |
(2) Rots模型 [79]
|
|
(4.6b) |
式中, ![]() 为开裂正应变。
为开裂正应变。
|
|
(4.6c) |
式中, ![]() 和
和 ![]() 为系数。
为系数。
(4) Al-Mahaidi模型 [77]
|
|
(4.6d) |
式中, ![]() 为系数。
为系数。
(5) 大连理工大学模型 [80]
|
|
(4.6e) |
式中, ![]() (mm)为裂缝跨度;
(mm)为裂缝跨度; ![]() (mm)为裂面剪切错动;
(mm)为裂面剪切错动; ![]() (MPa)为裂面剪力。基于裂缝带理论,当开裂应变在单元内均匀分布时,上式可改写为:
(MPa)为裂面剪力。基于裂缝带理论,当开裂应变在单元内均匀分布时,上式可改写为:
|
|
(4.6f) |
4.3 参数讨论
4.3.1 分析试件
利用通用有限元软件MSC.MARC [73] 的用户自定义子程序功能,将以上混凝土开裂受拉软化及裂面剪力模型嵌入到MARC中。为了验证本文提到的精细单元模型的合理性,首先进行了一系列的试算分析。试算内容包括:裂面剪力模型影响,开裂软化效果影响和单元尺寸影响。同宏观模型的参数分析考虑相同,选取Wu-2试件 [46] 和B-2试件 [44] 作为讨论前述5个不同混凝土裂面剪力模型的基础。
4.3.2 裂面剪力模型
前面提到,混凝土开裂后,共考虑5种剪力传递系数模型。在这些模型中,模型1、3、4中还有一些参数未定,因此首先需要对这些模型进行试算,以确定其参数。通过选取了大量参数试算后发现,对于模型1,取 ![]() ;对于模型2,取
;对于模型2,取 ![]() 和
和 ![]() ;对于模型3,取
;对于模型3,取 ![]() 时,计算得到的剥离承载力和试验结果吻合最好。模型2的承载力要明显高于试验结果,而模型5计算得到的承载力和试验值基本一致。
时,计算得到的剥离承载力和试验结果吻合最好。模型2的承载力要明显高于试验结果,而模型5计算得到的承载力和试验值基本一致。
由剥离承载力确定好模型参数后,将相同FRP端部拉力下试验得到的FRP应变和计算结果进行了对比(图4-5)。通过对比发现,模型5的纤维应变与试验结果吻合最好,因此,在后续分析中,使用模型5来模拟界面受剪行为。与宏观单元模型中完全依靠数值计算估计裂面剪力模型相比,精细单元模型中的裂面剪力模型的物理意义相对要明确得多,参数的试验依据也充分得多。
(a) Wu-2试件 (b) B-2试件
图4-5 不同裂面受剪模型FRP应变分布对比
4.3.3 混凝土受拉软化模型
图4-6所示为B-2试件在不同混凝土开裂受拉软化模型下的计算结果(裂面剪力模型为式4.6f)。可以看出,在剥离破坏发生前,二者几乎没有区别。在剥离破坏发生后,由于界面剥离裂缝出现的随机性,二者有一点差异。但是,这个差异对于最终计算结果影响很小。为了简化起见,在后续分析中都使用线性软化模型。
图4-6 不同裂面软化模型FRP应变分布对比
4.3.4 混凝土单元尺寸影响
为了解不同的单元尺寸对分析结果的影响,采用了单元大小不同的两个模型(单元尺寸分别为0.25mm和0.5mm)进行了计算对比,计算结果如图4-7所示。可见二者FRP应变差异并不显著。开裂应变云图的对比如图4-8所示,可见二者的结果同样也非常相似,只是精细单元(0.25mm)的裂缝分布更加清晰一些。因此,单元尺寸大小对本文的分析模型影响并不显著,故在后续的模型验证分析中,都使用较大的单元(0.5mm),以减少计算工作量。而只在讨论剥离机理时,使用较小的单元(0.25mm)来进行分析,以更好了解FRP-混凝土界面的剥离破坏过程。
图4-7 不同尺寸单元FRP应变分布对比

(a) 单元平均尺寸0.25mm

(b) 单元平均尺寸0.5mm
图4-8 不同尺寸单元裂缝分布图对比
4.3.5 对有限元模型的验证
为了进一步验证本文提出的模型,对表3-2所列的试件逐个进行了计算,计算结果与试验及经验公式结果的对比如表4-1及图4-9(部分结果)所示。可见计算结果与试验值及经验公式吻合良好。
另外,还需要说明的是,FRP片材在受拉的同时,由于局部弯曲作用,其顶部和中部应变是有所不同的,如图4-9a所示,在界面下混凝土存在较多裂缝的区域,FRP顶部和中部的应变的差别更大一些。但是,在试验量测中,虽然量测的都是FRP片材顶部的应变,但由于应变片的标距限制,一般很难测量出这种局部的弯曲影响。同时,计算得到的FRP片材中部应变由于没有局部弯曲的影响,更能体现出FRP受拉应变的特征,因此在图4-9其他的对比中,都使用的是计算得到的FRP片材中部应变。
表4-1 计算结果与试验结果对比
|
试件名称 |
试验 |
FEA* |
经验公式 [36] |
|||
|
极限荷载 (kN) |
有效锚固长度 (mm) |
极限荷载 (kN) |
有效锚固长度 (mm) |
极限荷载 (kN) |
有效锚固长度 (mm) |
|
|
Wu-1 |
14.1 |
61~90 |
13.8 |
76.8 |
11.44 |
81.5 |
|
Wu-2 |
23.5 |
120~165 |
24.7 |
146.0 |
22.35 |
159.0 |
|
B2 |
38.0 |
115~140 |
38.3 |
37.74 |
105.2 |
|
|
T-1 |
7.78 |
45~65 |
6.49 |
45.5 |
6.40 |
54.6 |
|
T-2 |
9.19 |
45~65 |
||||
|
T-3 |
10.11 |
45~65 |
8.23 |
45.5 |
8.12 |
54.6 |
|
T-4 |
13.95 |
40~60 |
||||
|
T-5 |
9.20 |
40~60 |
6.33 |
43.4 |
6.4 |
54.6 |
|
T-6 |
6.66 |
30~50 |
6.22 |
39.7 |
6.4 |
54.6 |
|
T-7 |
10.49 |
50~70 |
9.37 |
63.6 |
9.05 |
77.3 |
|
T-8 |
11.43 |
60~80 |
||||
|
T-9 |
7.97 |
45~65 |
8.44 |
46.3 |
8.08 |
68.9 |
|
T-10 |
9.19 |
50~70 |
||||
|
Yuan |
5.74 |
70~85 |
5.82 |
85.0 |
6.07 |
93.1 |
注:*根据Chen & Teng [36] 的经验公式进行宽度修正
(a) B-2试件 (b) T-1和T-2试件
(c) Wu-1试件 (d) Wu-2试件
图4-9 有限元模型和试验结果对比
4.4 界面剥离破坏过程
虽然在试验中很难对界面剥离破坏过程进行精确的观测,但通过有限元分析却可以得到剥离过程的种种细节。在上一章的宏观单元模型中,已经对界面下混凝土的开裂破坏过程有了一定的了解,但是由于宏观单元模型单元尺寸较大,难以反映界面下混凝土微裂缝的发生、发展、相互作用以及最后形成宏观剥离裂缝的整个破坏过程,而通过精细单元模型的分析结果则可以清晰地得到上述细节,并更好地了解界面剥离破坏的过程。
当然,实际的混凝土由于存在着骨料和水泥浆体等差异,破坏过程比有限元分析的可能要更加复杂。尽管如此,有限元结果仍然为了解界面剥离破坏过程提供了一个很好的手段。
以Wu-1试件为例,基于精细单元模型的有限元分析得到的荷载-滑移曲线如图4-10所示。为了说明整个破坏过程,在图4-10上选取了6个代表点,记为Point A~F。各点对应的裂缝云图如图4-11所示。
图4-11a为19%极限荷载时界面下混凝土开裂应变分布。混凝土内的这些裂缝可以分成3类:(a)界面浅层裂缝;(b)界面深层裂缝;(c)微裂缝区。这三种裂缝同样在图4-11b~f中存在。界面浅层裂缝的深度一般是在界面以下0.5~1mm区域,这些裂缝相对比较小且均匀。它们的成因是因为表层混凝土直接承受来自FRP片材的剪力和拉力。界面深层裂缝一般是在界面以下2~5mm深处,其宽度一般较大,它们主要是由界面剪力引起,并最终控制界面的粘结强度和滑移量。混凝土微裂缝区深度在5~15mm之间,它们主要是由界面剪力引起,部分微裂缝将随着剥离的发展而发育成界面深层裂缝。相对与宏观裂缝模型计算结果(图3-10)而言,精细单元模型对界面下的剥离破坏过程更加具体而形象。
基于上述分析结果,界面的剥离破坏机理和过程解释如下:
在较低的荷载水平下,界面下的混凝土被界面浅层裂缝分割为一系列非常小的悬臂柱,称之为微观悬臂柱。这些悬臂柱和界面所成的角度大约是45~60º(图4-11a)。随着荷载的增加,这些悬臂柱将变长形成界面深层裂缝(图4-11b,4-11c)。作用在悬臂柱顶端的剪力F可以分解为一个压力和一个弯曲剪力(见图4-12),其中压力将导致悬臂柱发生压碎破坏,称之为“压碎剥离”,而弯曲剪力将导致悬臂柱根部的弯曲破坏,称之为“弯曲剥离”。根据有限元分析结果,绝大部分的悬臂柱是根部弯曲破坏,形成一个平行于界面的宏观剥离裂缝(图4-11d~f),只有靠近加载端局部的悬臂柱是由于压碎而剥离破坏。
根据有限元得到的FRP应变分布,可以差分得到界面粘结应力:
|
|
(4.7) |
式中, ![]() 为FRP轴向应力,
为FRP轴向应力, ![]() 为FRP片材厚度。由式(4.7)计算得到Point A~F的界面粘结应力分布如图4-13所示(图中记为“原始差分结果”)。由于界面存在大量的局部裂缝,加上差分计算会放大误差,因此原始差分结果波动得非常厉害。为了去除这些局部波动,对原始差分结果用5mm的快速傅立叶变换(FFT)进行了数值平滑处理(图4-13中记为“平滑结果”)。从平滑结果可以清晰显示出不同荷载下粘结应力的分布、发展和有效锚固区的分布。对应图4-10 Point A~F的6个代表点的粘结应力分布状况如下:
为FRP片材厚度。由式(4.7)计算得到Point A~F的界面粘结应力分布如图4-13所示(图中记为“原始差分结果”)。由于界面存在大量的局部裂缝,加上差分计算会放大误差,因此原始差分结果波动得非常厉害。为了去除这些局部波动,对原始差分结果用5mm的快速傅立叶变换(FFT)进行了数值平滑处理(图4-13中记为“平滑结果”)。从平滑结果可以清晰显示出不同荷载下粘结应力的分布、发展和有效锚固区的分布。对应图4-10 Point A~F的6个代表点的粘结应力分布状况如下:
Point A(图4-13a):在加载早期,粘结应力集中在加载端附近。
Point B(图4-13b):随着荷载增加,有效锚固区变长,粘结应力也有所增加。
Point C和D(图4-13c和4-13d):加载端最大粘结应力达到粘结强度,该处界面进入软化段,粘结应力减小,而有效锚固区继续向自由端扩展。
Point E(图4-13e):最后,当加载端附近的界面完全剥离时,此处粘结应力变得非常的小,此处的界面下混凝土已经形成了一条宏观的剥离裂缝,也就是试验中观测到的界面剥离裂缝。在这个阶段时,荷载-滑移曲线已经进入严重的非线性。这个宏观剥离裂缝逐步从加载端向锚固端扩展,荷载增加将非常缓慢。此时有效粘结应力分布区域的长度就是有效锚固长度,剥离继续发展,有效锚固区将逐步向自由端移动,其长度及总粘结应力基本不再变化。
Point F(图4-13f):剥离继续发展,有效锚固区向自由端移动了大约10mm,其基本长度保持不变。从加载端到有效锚固区起点这段界面完全退出工作。
图4-10 Wu-2试件荷载滑移计算曲线
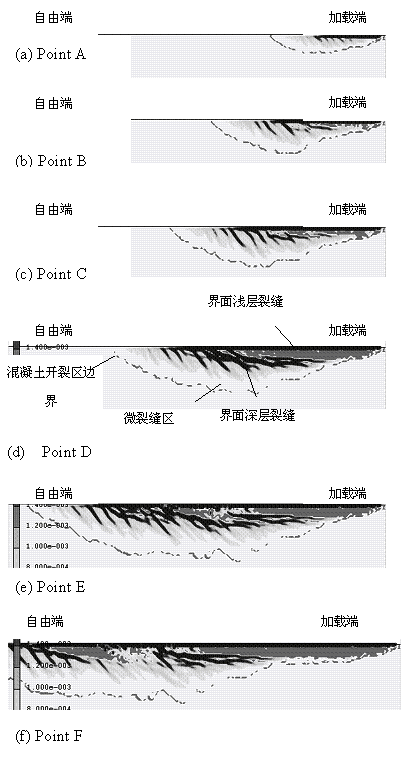
图4-11 界面混凝土裂缝发展
![]()
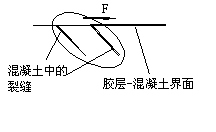
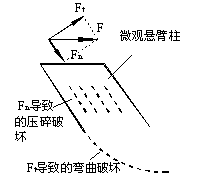
图4-12 微观悬臂柱破坏机理
(a) Point A (b) Point B
(c) Point C (d) Point D
(e) Point E (f) Point F
图4-13 界面粘结应力发展
4.5 小结
本章提出了一个精细单元有限元模型,通过细分单元网格,对FRP-混凝土界面的力学行为进行了分析。与宏观单元模型相比,精细单元有限元模型可直接利用现有通用有限元程序中的混凝土本构模型,不仅降低工作难度,且模型中参数有着可靠的试验依据,物理意义也很明确。分析结果表明,精细模型可以较好地模拟FRP-混凝土界面的剥离破坏过程,深入揭示界面剥离破坏的内在机理,得到界面粘结应力分布情况,从而为下一章提出界面粘结-滑移本构关系提供了重要基础。
|
目 录 |
I |
|
I |
|
|
1 |
|
5 |
|
25 |
|
41 |
|
59 |
|
80 |
|
94 |
|
134 |
|
150 |
|
178 |
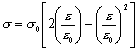 if
if