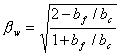FRP-混凝土界面行为研究/Studies on FRP-Concrete Interface
陆新征/Xin-zheng Lu
清华大学工学博士学位论文 / Tsinghua University Dissertation
2004
第三章 基于宏观单元的界面力学性能的数值模拟
3.1 FRP-混凝土界面有限元分析的技术难点
如前所述，目前对FRP-混凝土界面行为已经进行了大量的试验研究，但是基于有限元分析的数值模拟研究工作则相对较少，成果有限，未能充分揭示FRP-混凝土界面的受力机理。为此作者首先用现有的有限元程序，以面内剪切试验为对象，对FRP-混凝土界面行为进行了大量的试算。
有限元建模如图3-1所示，具体方法如下：
将FRP单元和混凝土单元直接联系在一起，以希望通过混凝土单元的断裂行为来模拟界面破坏；鉴于FRP和混凝土尺寸差异较大，用链杆或梁单元（对于二维分析）/膜单元或壳单元（对于三维分析）对FRP建模，而用实体单元为混凝土建模，混凝土单元的最小尺寸和被FRP剥离下来的混凝土层厚度相当，即大约在几个毫米左右（取2mm）。本文称这种有限元模型为宏观单元模型。
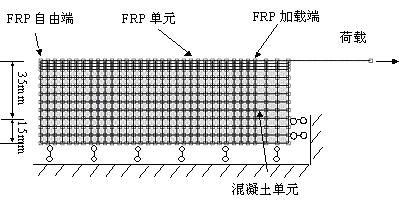
图3-1 宏观单元有限元模型
由于面内剪切试验中FRP片材的厚度非常小，因此在有限元模型中，无论是采用考虑FRP片材抗弯刚度的梁单元来模拟FRP片材，还是采用不考虑抗弯刚度的桁架单元来模拟，对计算结果都不会有太大影响。但是，如图3-2所示，如果连接到节点1的混凝土单元都开裂了，而FRP片材又采用桁架单元，则节点1在Y方向的刚度可能会非常小。这样会使整体刚度矩阵严重病态，进而带来严重的数值问题。但是，如果使用梁单元来模拟FRP片材，则即使混凝土单元都开裂了，节点1在Y方向上仍可由FRP片材来提供刚度，这对提高数值计算的收敛性有着很大好处。因此，本文中FRP片材都使用梁单元加以模拟。荷载按位移控制施加在FRP片材上。
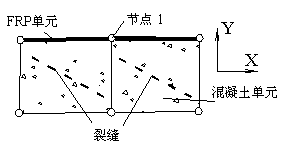
图3-2 混凝土实体单元开裂对节点刚度影响
由于界面下的整个破坏过程都依赖于界面下少数几层混凝土单元的断裂破坏，因此对混凝土的本构模型，尤其是本构模型中的裂缝模型提出了很高的要求。作者首先用现有的ANSYS [72] ，MSC.MARC [73] 两个通用有限元程序进行了大量的试算，结果发现，由于这两个软件中的混凝土本构模型都使用了固定裂缝模型(Fixed angle crack model, 简称FACM) [74] ，即初始裂缝方向和主拉应力方向垂直，裂缝一旦出现后其方向不再改变，从而导致严重的裂面剪应力锁死 [74] ，过高估计剥离区的残余应力，因而无法正确模拟界面的剥离失效和有效锚固区的移动 (图3-3)。而后，又用作者开发的基于无网格伽辽金算法的RCPEFG (Reinforced-Concrete-Planar-Element-Free-Galerkin) 程序进行了试算，由于RCPEFG程序可以考虑转动裂缝模型(Rotating angle crack model, 简称RACM) [74] ，因而计算结果比固定裂缝模型有了很大的改进，计算得到的界面下裂缝分布及FRP应变分布如图3-3，图3-4a及图3-4b所示。但是，由于RCPEFG程序的非线性收敛能力有限，在FRP剥离区开始移动后，其收敛变得非常困难，因而，用RCPEFG程序来分析整个剥离过程仍然有着较大的困难。
图3-3 MARC和RCPEFG计算结果与试验结果对比
(a) 界面下裂缝分布
(b) 开裂应变分布
图3-4 RCPEFG计算结果
根据上述试算的结果，发现FRP-混凝土界面有限元分析主要有以下一些困难 [60] ：
(1) 有限元模型参数难以确定
界面下混凝土剥离破坏层的厚度很小，其剥离受力行为又非常复杂，很难用试验量测获得有限元分析所必需的有关模型参数。
(2) 混凝土裂面行为复杂
初步分析表明，界面下的混凝土是在拉应力和剪应力的复合作用下产生开裂而导致界面剥离的。在开裂之初，一般与界面成30～45度裂缝；在混凝土开裂后，拉应力迅速减小，但剪应力由于裂面的摩擦作用，减小相对较慢，因此主应力方向会发生明显变化，使得后继裂缝的发展方向也随之发生较大变化。当FRP的粘结长度较大时，随着有效锚固区的移动，靠近加载端的混凝土裂缝宽度和裂面摩擦滑移量都较大，裂面剪应力变化规律也非常复杂。
(3) 数值收敛困难
由于界面存在开裂、滑移等多种复杂力学行为，使得非线性有限元分析时计算收敛相当困难，特别是对应于有效锚固区移动的计算收敛更是非常困难，这对程序的非线性分析能力提出了很高的要求。
因此，在使用宏观单元有限元模型基础上，要想对界面剥离问题进行正确模拟，对混凝土本构模型和计算程序有以下一些要求：
(1) 混凝土开裂模型要能够模拟混凝土开裂后的受拉软化行为；
(2) 裂面剪力传递系数应该随着裂缝宽度的增加而逐渐变化（降低）；
(3) 混凝土裂缝方向应可以随裂缝发展而变化，不应使用固定裂缝模型（FACM），而应考虑使用转动裂缝模型（RACM）；
(4) 随着剥离破坏的发展，界面以外的混凝土存在卸载状态，要考虑混凝土的加卸载行为；
(5) 同时，还要求有限元程序具有很强的非线性分析能力，能在复杂应力状态下保证计算收敛。
3.2 非共轴转动裂缝混凝土本构模型
3.2.1 概述
如前所述，现有的有限元程序的本构模型很难真实模拟FRP-混凝土界面的受力行为和剥离破坏过程，因此本章利用通用有限元程序MSC.MARC [73] 的二次开发功能嵌入自定义的混凝土本构模型RCFER-2002 [59] 。
作者提出的本构程序RCFER-2002与一般常见的混凝土本构模型的最主要差别在于，该本构模型既可以使用固定裂缝模型(FACM)，也可以使用转动裂缝模型(RACM)。此外，一般常见的转动裂缝模型中，主应力和主应变必须始终共轴（本文称之为共轴转动裂缝模型），而RCFER-2002中的转动裂缝模型中的主应力和主应变既可以共轴，也可以不共轴，这样可以更灵活的设定混凝土的裂面行为，从而可更好的实现对界面受力行为和剥离破坏的模拟。
3.2.2 强度准则
由于混凝土受压破坏在界面剥离问题中并不起控制作用，因此在RCFER-2002中选择了一个比较简单的二维强度准则，其破坏面采用的是Tasuji-Slate-Nilson [75] 建议的破坏面，如图3-5所示，图中 
。而破坏面分区则参考李-过破坏准则 [75] ，根据主应力 
和 
的大小分成5个区，如表3-1所示，从而将混凝土的二轴破坏分为3种破坏形式，5种应力组合分区，使计算结果物理意义更加明确。
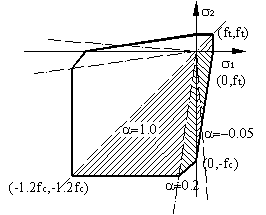
图3-5 破坏准则
表3-1 破坏曲面分区
|
分区 |
|
|
|
破坏形态 |
|
1 |
<0 |
<0 |
>0.2 |
双压片状压坏 |
|
2 |
<0 |
<0 |
<0.2 |
单压柱状压坏 |
|
3 |
>0 |
<0 |
>-0.05 |
单压柱状压坏 |
|
4 |
>0 |
<0 |
<-0.05 |
拉坏 |
|
5 |
>0 |
>0 |
拉坏 |
3.2.3 应力应变关系
混凝土的等效受压应力应变关系骨架线使用Saenz公式 [12] ：
|
|
(3.1) |
式中， 
为切线模量； 
为等效单向应变； 
为等效单向峰值压应变； 
为初始弹性模量； 
为峰值点割线弹性模量。
受拉软化应力应变关系采用江见鲸 [12] 建议公式：
|
|
(3.2) |
式中， 
为混凝土抗压强度； 
为裂缝张开方向的正应变；
为混凝土开裂应变； 
为系数，与混凝土的断裂能相关。
3.2.4 裂缝模型和裂面剪力传递系数
本构程序RCFER-2002的主要特点是，使用者可以采用固定裂缝模型(FACM)，也可以采用转动裂缝模型(RACM)。FACM模型假设裂缝一旦出现，其方向不随主应力变化而变化，该模型可以较好地克服网格倾斜(Mesh bias)带来的影响 [76] ，因此适合于分析受拉开裂为主的问题。但是，由于FACM模型可能会过高估计裂面剪力传递能力 [74] ，因此当主应力方向变化较大，裂面剪力很大的时候会带来较大误差。而在RACM模型中，裂缝方向始终和主拉应变方向垂直，可以降低裂面的剪力锁死问题(Stress Locking)，比较适合于主应力方向变化较大的问题，本文所分析的FRP-混凝土界面的面内剪切剥离破坏即属于这类情况。
RCFER-2002除了可以任意选择固定裂缝模型或转动裂缝模型外，在裂面受剪模型的选择上也提供了较大的自由度。根据弥散裂缝模型，开裂混凝土的折算剪切模量 
， 
为剪力传递系数，该系数反映了开裂后混凝土的裂面咬合作用的大小。针对不同裂缝模型，RCFER-2002提供了以下剪力传递系数 
计算方法：
(1) 对于常用的固定裂缝模型，作者建议采用如下剪力传递系数公式：
|
|
(3.3a) |
式中， 
， 
分别为混凝土刚刚开裂和裂缝充分发展时的剪力传递系数； 
为常数，反映 
降低的速度。上式具有比较好的通用性，如取 
，则 
为一定值，即为常用的固定剪力传递系数模型。如果取 
， 
， 
，则与Al-Mahaidi [77] 建议的裂面剪力传递系数变化关系相接近，裂面剪力传递系数将随裂缝开展宽度增加而降低。
(2) 对于转动裂缝模型，如果要保持主应力和主应变在开裂后始终一致，即常见的共轴转动裂缝模型(co-axial RACM)，则裂面剪力传递系数可取为 [74] ：
|
|
(3.3b) |
式中， 
为裂缝张开方向正应力，
和
为平行裂缝方向的正应力和正应变。
(3) 如果裂面行为复杂，式(3.3b)得到的裂面剪力模型无法加以准确描述，则可以使用式(3.3a)的剪力传递系数模型来描述转动裂缝模型中的裂面剪切行为。不过，此时主应力和主应变则不再保持共轴，本文称之为非共轴转动裂缝模型，它描述裂面受剪行为的灵活性更大一些。
图3-6所示为一个混凝土单元在3种不同裂缝模型下的受剪行为，其中裂面受拉软化都按式(3.2)计算。而裂面受剪分别用正交固定裂缝模型(式3.3a)，共轴转动裂缝模型 (式3.3b)和非共轴转动裂缝模型(式3.3a)加以分析，计算参数分别为： 
，
, 
，
=750或2000， 
，
。
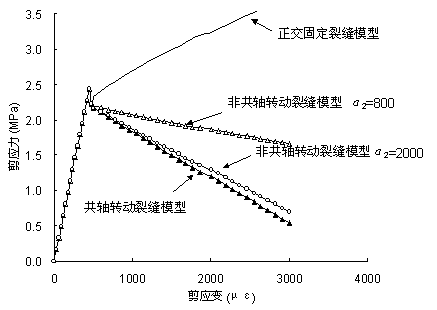
图3-6 不同裂缝模型比较
从图3-6可以清楚看出，在正交固定裂缝模型中，存在有严重的裂面剪应力锁死问题，即随着剪应变的增加，裂面剪应力不断增大，这不符合FRP－混凝土界面的受力性能。而在其它模型中不存在裂面剪应力锁死问题，但共轴转动裂缝模型中，由于主应力和主应变方向需要保持一致，故剪力传递系数不能由使用者自由调整，因而非共轴转动裂缝模型比共轴转动裂缝模型处理受剪软化的灵活性更大一些。考虑到面内剪切试验中FRP-混凝土界面行为的特点，本章建议采用非共轴转动裂缝模型来模拟FRP-混凝土界面剥离行为。
3.3 有限元分析结果
3.3.1 面内剪切试验的有限元模型
在本章研究中，使用平面应力有限元模型来模拟面内剪切试验，见图3-1。由于实际试验中FRP和混凝土之间的宽度可能不等，为了考虑宽度效应影响，有限元计算得到的FRP应变用Chen & Teng [36] 建议的宽度修正系数
加以调整，以便与试验结果相比较。
|
|
(3.4) |
式中， 
和
分别为FRP和混凝土的宽度。
3.3.2 参数讨论
对于非共轴转动裂缝模型，混凝土开裂后裂面受拉和受剪行为由式(3.2)和式(3.3a)给出。其中有 
、
、
和
等4个参数有待确定。在这4个参数中，
的物理意义很明确，它表示在开裂应变很大时的裂面剪力传递系数，理论上 
应该等于零。但在本章计算中，取 
＝0.001来提高非线性分析的稳定性。 
可以根据断裂能来估计。混凝土开裂时的断裂能为，
|
|
(3.5) |
式中， 
为裂缝宽度。根据欧洲模式规范建议公式
[78] ， 
，这里 
(MPa)为混凝土抗压强度；对于一般骨料混凝土， 
。如果混凝土裂缝带的宽度为 
，且开裂应变在 
为均匀分布的话，则裂缝宽度 
可以由下式计算：
|
|
(3.6) |
进而，由式(3.2)，(3.5)，(3.6)可得,
|
|
(3.7) |
一般认为， 
应该为混凝土单元的平均尺寸。但是，根据分析发现，如果取为单元的平均尺寸，将会过高估计界面的剥离强度。因此，在本章的研究中， 
取为60mm，即大概是3倍混凝土的最大骨料粒径。
用来描述混凝土刚刚开裂时的裂面抗剪能力，在Rots等 [79] 建议的模型中，取为1.0；而在Al-Mahaidi建议 [77] 的模型中，取为0.4。本章对这两个数值都进行了试算，以寻找较为合适的
取值。
在 
、 
和
都确定后，就只有 
未知了，因此本章通过试算来确定其取值。考虑到试验的随机性，用Chen & Teng
[36] 建议的经验公式来校核试验的剥离承载力。通过对比发现，Wu-2
[46] 和B-2 [44] 这两个试件的剥离强度与经验公式结果比较接近，且这两个试件都提供了FRP应变分布。因此，本章用这两个试件作为基准来寻找合适的
。其中，Wu-2试件的粘结长度为250mm，混凝土抗压强度为57.6MPa，CFRP的名义厚度为0.501mm，弹性模量为390GPa；B-2试件的粘结长度为200mm，混凝土抗压强度为45.9MPa，CFRP的名义厚度为0.33mm，弹性模量为230GPa。
通过对不同的 
取值进行了大量试算，发现 
在600~1000附近时，计算得到的剥离承载力和试验结果比较接近。而后，将 
在600~1000之间每隔50进行试算，最后发现当 
且 
时计算结果和试验结果最为接近。计算得到的FRP应变分布和试验的FRP应变分布对比如图3-7所示。
综上， 
、
、
和
等4个参数的取值如下：
， 
， 
， 
。
(a) Wu-2 试件计算结果与试验结果比较
(b) B-2 试件计算结果与试验结果比较
图3-7 宏观单元有限元计算结果和试验结果对比
3.3.4 模型验证
在确定了裂缝模型的参数以及混凝土本构模型后，就可以对大量的面内剪切试件进行计算。表3-2中列出了由不同试验者 [35,44,46] 试验的14个不同试件的有关参数，这些试件都提供了剥离承载力（表3-2中的Pu）和FRP应变分布。用前面讨论的有限元模型对这些试件进行了分析，得到的主要结果见表3-3，可见用本文建议的有限元模型计算得到的剥离承载力和经验公式的结果吻合得更好一些。表3-3中试验有效锚固长度是从FRP应变分布图上得到的，而试验的FRP应变测点密度有限，且测得的FRP应变也往往由于种种局部干扰作用而波动较大，因此试验的有效锚固长度很难给出一个精确的数值，而用一个区间范围来描述则更合适一些。由有效锚固长度的对比可以看出，有限元分析得到的界面有效锚固长度都位于试验范围内，而经验公式预测的有效锚固长度也大部分位于试验范围以内。
表3-2 分析试件的参数
|
编号 |
试件名称 |
FRP片材 |
混凝土块体 |
Pu (kN) |
βw |
||||
|
厚度 (mm) |
宽度 (mm) |
粘结长度 (mm) |
弹性模量 (GPa) |
立方体强度(MPa) |
宽度 (mm) |
||||
|
1 |
Wu-1 |
0.22 |
40 |
250 |
230 |
72.0 |
100 |
14.1 |
1.069 |
|
2 |
Wu-2 |
0.501 |
40 |
250 |
390 |
72.0 |
100 |
23.5 |
1.069 |
|
3 |
B-2 |
0.33 |
100 |
200 |
230 |
57.4 |
500 |
38.0 |
1.225 |
|
4 |
T-1 |
0.167 |
50 |
130 |
97 |
37.6 |
100 |
7.78 |
1 |
|
5 |
T-2 |
0.167 |
50 |
130 |
97 |
37.6 |
100 |
9.19 |
1 |
|
6 |
T-3 |
0.167 |
75 |
130 |
97 |
37.6 |
100 |
10.11 |
0.845 |
|
7 |
T-4 |
0.167 |
75 |
130 |
97 |
37.6 |
100 |
13.95 |
0.845 |
|
8 |
T-5 |
0.167 |
50 |
100 |
97 |
37.6 |
100 |
9.20 |
1 |
|
9 |
T-6 |
0.167 |
50 |
70 |
97 |
37.6 |
100 |
6.66 |
1 |
|
10 |
T-7 |
0.33 |
50 |
130 |
97 |
37.6 |
100 |
10.49 |
1 |
|
11 |
T-8 |
0.33 |
50 |
130 |
97 |
37.6 |
100 |
11.43 |
1 |
|
12 |
T-9 |
0.111 |
50 |
130 |
235 |
37.6 |
100 |
7.97 |
1 |
|
13 |
T-10 |
0.111 |
50 |
130 |
235 |
37.6 |
100 |
9.19 |
1 |
|
14 |
Yuan |
0.165 |
25 |
190 |
256 |
29.7 |
150 |
5.74 |
1.254 |
注：数据来源: 1~2: 文献 [46] 3: 文献 [44] ; 4~13: 见2.2节; 14: 文献 [35] .
表3-3 计算结果与试验结果及经验公式结果对比
|
试件名称 |
试验 |
FEA* |
经验公式 [36] |
|||
|
极限荷载 (kN) |
有效锚固长度 (mm) |
极限荷载 (kN) |
有效锚固长度 (mm) |
极限荷载 (kN) |
有效锚固长度 (mm) |
|
|
Wu-1 |
14.1 |
61~90 |
11.8 |
78.0 |
11.44 |
81.5 |
|
Wu-2 |
23.5 |
120~165 |
23.8 |
123.0 |
22.35 |
159.0 |
|
B2 |
38.0 |
115~140 |
38.6 |
117.0 |
37.74 |
105.2 |
|
T-1 |
7.78 |
45~65 |
7.56 |
46.3 |
6.40 |
54.6 |
|
T-2 |
9.19 |
45~65 |
||||
|
T-3 |
10.11 |
45~65 |
9.58 |
46.3 |
8.12 |
54.6 |
|
T-4 |
13.95 |
40~60 |
||||
|
T-5 |
9.20 |
40~60 |
7.03 |
45.3 |
6.4 |
54.6 |
|
T-6 |
6.66 |
30~50 |
6.50 |
39.0 |
6.4 |
54.6 |
|
T-7 |
10.49 |
50~70 |
10.40 |
61.3 |
9.05 |
77.3 |
|
T-8 |
11.43 |
60~80 |
||||
|
T-9 |
7.97 |
45~65 |
7.84 |
54.0 |
8.08 |
68.9 |
|
T-10 |
9.19 |
50~70 |
||||
|
Yuan |
5.74 |
70~85 |
5.22 |
85.0 |
6.07 |
93.1 |
注：*根据文献 [36] 建议公式进行宽度修正
图3-8a所示为Wu-2试件的FRP计算应变与试验应变对比。从对比图中可以看出，在加载初始阶段，当荷载小于剥离荷载20%的时候，只有加载端附近的一小部分混凝土界面参与受力。当P/Pu大约为0.83时，加载端附近开始出现剥离，此时加载端附近FRP应变几乎保持不变。随着剥离发展，剥离区也逐步从加载端向自由端发展，这与试验观测现象一致。其他试件的有限元分析结果和试验结果对比如图3-8所示（未列出所有试件），可见有限元计算结果和试验结果还是吻合得很好的。
(a) T-1 & T-2试件 (b) T-7 & T-8试件
(c) Wu-1试件
图3-8 计算与试验结果对比：FRP应变分布
以试件Wu-2为例，当FRP有效发挥长度（参与界面工作的FRP长度）大约为180mm时，不同裂缝模型预测的FRP应变分布对比如图3-9所示。从对比中可以看出，常用的正交固定裂缝模型或共轴转动裂缝模型都不能很好的模拟实际的FRP应变分布。这是因为，正交固定裂缝模型存在剪应力锁死问题，过高估计裂面的剥离承载力；而共轴转动裂缝模型无法自由调整受剪软化速率，则会过低估计裂面抗剪能力，进而低估界面的剥离承载力。因此，本章建议的非共轴转动裂缝模型更适合分析FRP-混凝土的界面剥离破坏问题。
图3-9 不同裂缝模型计算结果对比
3.4 界面力学性能和剥离机理的讨论
为了更好地了解界面剥离破坏机理和过程，将Wu-2试件有限元模型的加载端附近局部进行放大，如图3-10所示，图中，箭头代表单元的主应力，箭头的长短表示主应力的相对大小，而箭头的方向表示主应力的符号（箭头朝外为正（拉）应力，箭头朝内为负（压）应力）；粗实线代表裂缝，由于本章采用的是转动裂缝模型，所以裂缝方向始终和主应力方向垂直。根据有限元全过程分析结果和FRP下混凝土层的裂缝发展和破坏过程，FRP-混凝土界面的剥离破坏机理和过程如下：
(1) 在加载的初始阶段，加载端附近的混凝土并未开裂(P<1.52kN)，当荷载达到1.52kN时，加载端下混凝土的主（拉）应力达到混凝土抗拉强度，其方向与界面大约成30度角，第一条裂缝将在垂直于主拉应力的方向出现，如图3-10a所示。
(2) 一旦第一条裂缝出现，则垂直于裂缝方向的拉应力迅速减小，由于剪应力软化速度比拉应力要慢，因此在加载端下的混凝土基本处于纯剪应力状态，表现为主拉应力和主压应力大小相近，如图3-10b所示。
(3) 当荷载达到大约90%的极限荷载，即P=21.63kN时，加载端下两个单元的第二主应力超过了抗拉强度，在这些单元中出现了第二条裂缝。出现第二条裂缝后，这些单元所提供的粘结应力已经非常小了，表明该单元混凝土退出工作，即开始产生剥离，因而在这两个单元上方的FRP应变变化也很小（图3-10a，P/Pu=0.85）。有效锚固区将向自由端移动。
(4) 当荷载达到剥离承载力时，在加载端附近的5列单元中都出现了第二条裂缝，在这些单元上方界面的粘结应力也变得非常小。此时有效锚固区已经移动到从第6列单元开始，这种剥离过程是FRP-混凝土面内剪切破坏的典型过程，在很多试验研究中都观察到这一现象 [35,37] 。
(a) P=1.52kN (b) P=4.52kN
(c) P=21.63kN (d) P=23.8kN
图3-10 Wu-2试件在不同荷载等级下的裂缝分布
3.5 小结
本章主要完成了以下工作：
(1) 通过各种软件试算，分析了现有有限元软件中混凝土本构模型在分析FRP-混凝土界面剥离问题中所存在的主要困难；
(2) 针对现有程序中混凝土本构模型所存在的问题，开发了二维混凝土本构程序RCFER-2002，在混凝土裂缝模型的选取上有着较大的自由度，可以选择使用固定裂缝模型、共轴转动裂缝模型和非共轴转动裂缝模型。并通过算例比较了不同裂缝模型受剪行为的差异，指出非共轴转动裂缝模型更适用于分析FRP混凝土界面剥离问题；
(3) 通过参数讨论得到了裂缝模型的相关参数，并通过14个试验算例验证了本章提出的有限元模型的正确性。用算例对比说明，采用宏观单元有限元模型，常用的固定裂缝模型和共轴转动裂缝模型不适于分析FRP-混凝土界面剥离问题；
(4) 基于有限元分析结果对FRP混凝土界面剥离破坏机理和过程进行了讨论，揭示了界面下混凝土开裂破坏过程以及相应的破坏发展规律。
|
目 录 |
I |
|
I |
|
|
1 |
|
5 |
|
25 |
|
41 |
|
59 |
|
80 |
|
94 |
|
134 |
|
150 |
|
178 |