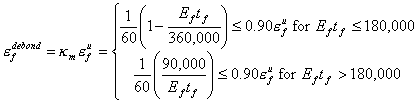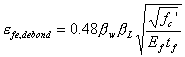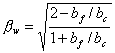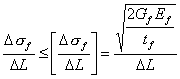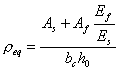FRP-混凝土界面行为研究/Studies on FRP-Concrete Interface
陆新征/Xin-zheng Lu
清华大学工学博士学位论文 / Tsinghua University Dissertation
2004
第六章 抗弯加固剥离研究综述
6.1 引言
外贴FRP片材对钢筋混凝土(RC)梁进行抗弯加固是FRP加固混凝土结构的一种主要应用形式。在对梁进行抗弯加固时,FRP多贴于梁底部,也有少数贴于梁的侧面,和受拉钢筋一起承担截面拉应力。FRP的拉力通过界面粘结传递给混凝土。除了常见的混凝土压碎或FRP拉断等破坏形式外,FRP片材和混凝土之间的剥离破坏在试验中也非常常见 [91-121] 。根据Teng et al. [112] 的研究工作,这类剥离破坏可以分为以下四种形式(图6-1):
(1) 保护层剥离 (Cover separation) [91,95,100,106,118]
(2) FRP端部界面剥离 (Plate end interface debonding) [92,122]
(3) 中部裂缝处剥离 (Intermediate crack debonding,简称 IC debonding) [93,100,103,107-121]
(4) 关键斜裂缝剥离 (Critical diagonal crack debonding,简称 CDC debonding) [28,93,107,123,124]
这些剥离破坏形式可以分为两类:一类是由FRP片材端部应力集中引起的,包括保护层剥离和FRP端部界面剥离;另一类是由于梁底裂缝发展引起的,包括中部裂缝剥离和关键斜裂缝剥离。
FRP片材端部应力集中剥离一般是由于FRP片材截断导致截断截面受弯刚度不连续,形成应力集中而引起的,其中以保护层剥离更为常见。由于这种剥离形式与加固的片材刚度有关,刚度越大,剥离越容易出现,因此在粘钢加固研究中就已经对这类破坏形式进行了深入研究,目前已经提出了很多强度模型,在Smith & Teng [125,126] 的工作中对这些模型进行了详细的讨论和比较。另外,试验研究表明,只要在FRP片材的端部附加U型箍或采取其它机械锚固措施,就可以有效避免端部剥离情况发生 [91,100,106,127] 。因此,这类剥离形式在工程中比较易于处理。

图6-1 RC梁受弯加固的剥离破坏形式
关键斜裂缝剥离破坏主要是由于钢筋混凝土梁抗剪能力不足,出现较大的受剪斜裂缝,进而引起斜裂缝两侧刚体错动而导致的。由于实际工程设计中一般要求梁为强剪弱弯,因此这种由于抗剪承载力不足导致的剥离破坏一般也可以避免。
中部裂缝剥离(IC debonding)是由于受弯裂缝张开较大,在裂缝附近形成局部粘结应力集中而导致的剥离破坏。这种剥离破坏形式在粘钢加固中并不常见,而在FRP抗弯加固中却经常发生。这是因为钢材的强度一般比较低,达到屈服时应变不大,因而裂缝附近的滑移也就不显著。而FRP强度高,断裂应变很大,在断裂前裂缝附近的滑移也很大,使得IC debonding先于FRP断裂出现。目前对这种破坏形式的研究还很少。而且,这种剥离破坏和混凝土受弯裂缝开展相关,即便使用U型箍或其他附加锚固措施也不能完全避免,因此很有必要对这种剥离破坏形式进行深入研究。本文以下主要分析和研究IC debonding的剥离机理、计算理论和方法。除非专门指出,否则本文以下所提到的受弯剥离都是针对IC debonding。
梁底粘贴FRP片材受弯加固的RC梁,FRP与混凝土界面上主要存在以下两种界面粘结应力:
(1)
由剪力引起的界面粘结应力 ![]() (见图6-2)。取RC梁弯剪段的一个微段
(见图6-2)。取RC梁弯剪段的一个微段
![]() ,作用在微段上的力有,混凝土的压应力
,作用在微段上的力有,混凝土的压应力 ![]() ,剪力
,剪力 ![]() ,弯矩
,弯矩 ![]() ,钢筋拉应力
,钢筋拉应力 ![]() 以及FRP拉应力
以及FRP拉应力 ![]() 。由微段FRP受力平衡可得剪力引起的界面粘结应力
。由微段FRP受力平衡可得剪力引起的界面粘结应力 ![]() ,其中,
,其中, ![]() 为FRP片材厚度。需要说明的是,由于
为FRP片材厚度。需要说明的是,由于 ![]() 由剪力引起,因而只在弯剪段出现。
由剪力引起,因而只在弯剪段出现。
(2)
裂缝张开引起的界面粘结应力 ![]() (见图6-3)。弯曲裂缝在弯矩作用下有张开的趋势,而跨越裂缝两侧的FRP片材将阻止裂缝张开。这样,在裂缝两侧FRP-混凝土界面上会出现界面粘结应力
(见图6-3)。弯曲裂缝在弯矩作用下有张开的趋势,而跨越裂缝两侧的FRP片材将阻止裂缝张开。这样,在裂缝两侧FRP-混凝土界面上会出现界面粘结应力 ![]() 。
。 ![]() 将随着裂缝张开宽度加大而增大,并导致在裂缝两侧出现剥离破坏。
将随着裂缝张开宽度加大而增大,并导致在裂缝两侧出现剥离破坏。
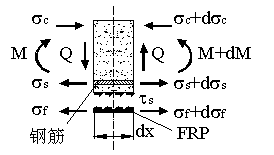
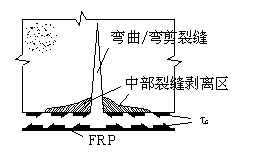
图6-2 剪力引起的界面粘结应力 图6-3 由裂缝张开引起的界面粘结应力
6.2 抗弯加固剥离试验研究
如前所述,在FRP加固应用早期,对IC debonding的剥离破坏认识很少,尽管大量试验中出现了受弯剥离破坏,但对引起受弯剥离破坏的各种原因和机理描述含混不清。1998年后,对FRP受弯加固的剥离破坏分类才逐步明确,相应的试验记录也逐渐被报道。这些试验资料,可以根据是否布置附加锚固措施分为两类:一类是只在梁的受拉面粘贴FRP,基本没有其他的附加锚固措施,或者仅仅在FRP端部施加FRP U型箍或机械锚固以避免端部剥离破坏,试验目的是为了了解IC debonding的发生条件;另一类是在整个梁长,特别是在最大弯矩截面附近布置FRP U型箍或其他锚固措施,试验的目的是为了了解如何通过附加锚固措施来提高IC debonding的承载力。就现阶段的研究而言,一方面,由于附加锚固的方法非常繁多,有U型箍、有打栓钉等等,而这些附加锚固措施对界面粘结破坏影响机理的研究还非常少,因而深入讨论这些锚固措施对IC debonding的影响的条件还不具备。另外,根据现在的试验研究,使用附加锚固措施来提高剥离延性是比较可行的方法,对IC debonding承载力的提高效果并不稳定 [110] 。因此,基于以上两点,在本文的研究中,主要讨论没有施加附加锚固措施的IC debonding破坏,而附加锚固措施的剥离破坏则需要在充分掌握一般IC debonding破坏机理的基础上才能进一步深入,现阶段在工程实用中附加锚固措施可作为安全储备。
根据文献调研,一共找到了80个剥离破坏区没有附加锚固措施的IC debonding试验记录(部分试件在FRP端部有U型箍,但如前所述,这对IC debonding没有影响)(试验资料来源:文献 [93,100,103,107-121] ,参见附录B)。这些试验记录的参数齐全,覆盖面广,其中主要参数(混凝土强度,FRP刚度,梁高,净跨,受拉钢筋配筋率)分布情况如图6-4示。以这些试验作为基础,对IC debonding进行研究有着较好的代表性。
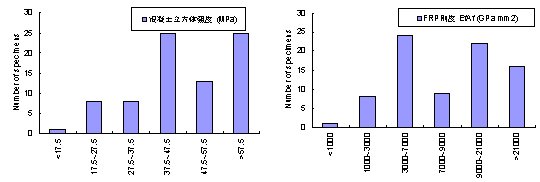
(a) 混凝土立方体强度 (b) FRP轴向刚度
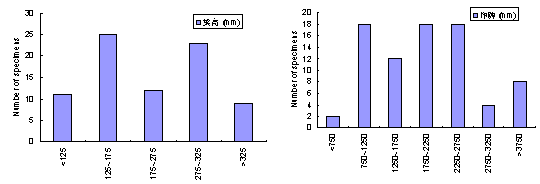
(c) 梁高 (d) 净跨
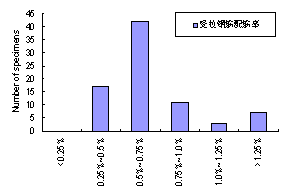
(e) 受拉钢筋配筋率
图6-4 主要参数分布
6.3 抗弯加固剥离数值分析
除了试验研究外,各国学者对IC debonding破坏都进行了数值模拟 [54,56,99,128-131] 。一般来说,在这些有限元分析中,使用二维或三维实体单元建立混凝土模型,用梁单元(2D)/壳单元(3D)或桁架单元(2D)/膜单元(3D)建立FRP片材模型,并在FRP单元和混凝土单元之间布置界面单元,用于模拟界面的粘结-滑移行为。这样,界面的剥离就通过界面单元的失效加以模拟。由于IC debonding和RC梁的弯曲裂缝密切相关,又与界面行为关系密切。因此如何正确模拟受弯裂缝以及受弯裂缝和界面剥离之间的关系,是进行IC debonding模拟的关键。在前面章节中已经详细说明,本文之前已有的界面粘结-滑移模型都存在问题,因此准确模拟受弯剥离势必存在很大困难。这里再介绍一下目前裂缝模拟所存在的问题。
在现有的钢筋混凝土有限元分析中,对裂缝的模拟一般有两种方法 [12] ,一种是弥散裂缝模型(Smeared crack model),一种是分离裂缝模型(Discrete crack model)。
弥散裂缝模型是将实际混凝土中的裂缝分布到整个混凝土单元内,通过改变混凝土单元的本构关系,削弱或去除混凝土单元在裂缝张开方向的受拉刚度加以模拟,其优点在于弥散裂缝模型不必随着裂缝出现和发展而改变有限元网格划分,便于有限元分析;其缺点是由于将真实裂缝分布到整个混凝土单元内部,因此除非将网格划分得非常细密,否则无法直接得到裂缝附近的变形场等细节。这对于IC debonding这种和裂缝附近滑移集中关系密切的破坏形式而言是十分不利的。
分离裂缝模型是使用单元边界来模拟实际裂缝,其优点在于可以明确知道某条裂缝的走向、以及裂缝附近的变形情况。但是,由于分离裂缝模型需要随着裂缝的开展而不断改变有限元网格划分,因此实际操作非常困难。
由于弥散裂缝模型非常便于有限元实施,因此现阶段的大部分IC debonding有限元分析都是基于弥散裂缝模型 [54,56,99,128-131] 。但是,如前文所述,常规单元尺寸下的弥散裂缝模型很难对裂缝附近滑移场进行准确描述,通过单元形函数插值得到的滑移场因无法反映裂缝附近的滑移集中现象,因而其计算结果总是比实际的滑移场要小,进而过高的估计了界面的承载力。一些研究者 [54,56] 通过调整界面粘结强度的方法使受弯剥离计算值和试验值相吻合,但仍然没有找到受弯剥离界面强度的调整规律。
分离裂缝模型在理论上可以很好的预测裂缝附近的滑移集中,一些研究者也通过分离裂缝模型较好地模拟了裂缝附近的滑移集中效应 [71,129,132] 。但是,由于分离裂缝模型需要根据裂缝发展改变单元网格划分,对于钢筋混凝土梁这种存在大量受弯裂缝的构件来说,用分离裂缝模型逐条追踪裂缝发展几乎是不可能的。因此,现有的分离裂缝模型研究成果基本上都是基于预设裂缝模型进行的,即在有限元网格划分中预设裂缝位置,让受弯裂缝沿着预设裂缝路径发展。这当然无法真实反映混凝土梁中裂缝发展的实际情况以及裂缝和荷载之间的相互关系,因而也就无法真实反映IC debonding全过程。
6.4 抗弯加固剥离承载力设计方法
6.4.1 概述
由于IC debonding在FRP加固混凝土构件中大量出现,因此各国研究者目前针对这种破坏模型提出了一些设计公式。在讨论这些设计公式之前,首先统一定义截面的参数符号(图6-5), ![]() 和
和 ![]() 为梁表面到受拉和受压钢筋的距离;梁的有效高度(从梁顶面到受拉钢筋重心距离)为
为梁表面到受拉和受压钢筋的距离;梁的有效高度(从梁顶面到受拉钢筋重心距离)为 ![]() ;混凝土受压区高度为
;混凝土受压区高度为 ![]() ;顶面混凝土压应变,受压钢筋应变,受拉钢筋应变和FRP应变分别用
;顶面混凝土压应变,受压钢筋应变,受拉钢筋应变和FRP应变分别用 ![]() ,
, ![]()
![]() 和
和 ![]() 表示。
表示。
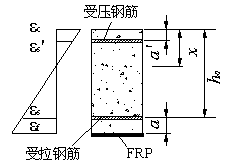
图 6-5 截面符号
根据现有的文献资料,目前共有5个设计公式可以用来计算IC debonding的承载力,现逐一介绍如下:
6.4.2 ACI 440建议的公式
美国混凝土协会(ACI) 440委员会
[2] 建议的设计公式并未区分前面提到的不同剥离破坏形式,而是根据试验数据回归,给出了一个统一的受弯剥离应变 ![]() 计算公式:
计算公式:
|
|
(6.1) |
式中, ![]() ,
, ![]() (MPa)和
(MPa)和 ![]() (MPa)为FRP片材的极限强度和弹性模量。这里需要补充的是,在ACI 440的原文中,
(MPa)为FRP片材的极限强度和弹性模量。这里需要补充的是,在ACI 440的原文中, ![]() 为单层FRP片材厚度,而总片材厚度为
为单层FRP片材厚度,而总片材厚度为 ![]() ,
, ![]() 为片材层数。本文中为了与后面的其它模型中的符号一致,用
为片材层数。本文中为了与后面的其它模型中的符号一致,用 ![]() 来表示FRP片材的总厚度。
来表示FRP片材的总厚度。
6.4.3 黄-叶建议的公式
黄-叶建议的公式 [133] 是根据有限元分析和试验测得的界面粘结应力分布而提出的。在该公式中,FRP-混凝土界面粘结应力分布图被简化为一梯形,梯形的底边长度为FRP粘贴延伸长度 ![]() ,顶边长度为150mm,即近似为有效粘结长度,则剥离应变
,顶边长度为150mm,即近似为有效粘结长度,则剥离应变 ![]() 可以写作:
可以写作:
|
|
(6.2) |
式中,tmax为界面粘结强度。由于当时对界面的粘结-滑移行为尚缺乏深入的研究,因此黄-叶根据文献 [110] 的试验结果,偏保守的建议界面最大粘结应力
![]() 。
。
6.4.4 Teng等建议的公式
Teng等 [112] 对Chen & Teng [36] 的面内剪切剥离承载力设计公式做了修正,由试验得到的FRP剥离应变回归出相应参数,并经过29个IC debonding破坏试验验证,最终其模型如下所示:
|
|
(6.3a) |
|
|
|
(6.3b) |
|
|
|
(6.3c) |
|
|
|
(6.3d) |
式中, ![]() (MPa)为混凝土圆柱体抗压强度,
(MPa)为混凝土圆柱体抗压强度, ![]() (mm)和
(mm)和 ![]() (mm)为FRP片材和RC梁的宽度。
(mm)为FRP片材和RC梁的宽度。
6.4.5 JSCE建议的公式
日本土木工程学会(JSCE)建议的设计公式 [5] 是基于FRP-混凝土界面破坏能概念建立的。其受弯剥离承载力通过验算FRP片材应力梯度来预测,如下式所示:
|
|
(6.4) |
式中, ![]() 为界面剥离破坏能,JSCE建议取为0.5N/mm;
为界面剥离破坏能,JSCE建议取为0.5N/mm; ![]() 为最大弯矩截面到FRP应力梯度验算截面的距离,JSCE建议根据FRP片材纤维厚度可取为150~250mm,在本文后面的计算中统一取
为最大弯矩截面到FRP应力梯度验算截面的距离,JSCE建议根据FRP片材纤维厚度可取为150~250mm,在本文后面的计算中统一取
![]() 。
。
6.4.6 fib建议的公式
欧洲国际混凝土协会(fib)建议的设计公式 [4] 认为,IC debonding主要由于受弯裂缝张开过宽导致。fib认为,界面的极限滑移量为
![]() ,如果弯曲裂缝宽度
,如果弯曲裂缝宽度 ![]() 大于
大于 ![]() ,则将发生IC debonding破坏。fib [4] 建议
,则将发生IC debonding破坏。fib [4] 建议 ![]() 。
。
fib建议的FRP加固RC梁受弯裂缝宽度 ![]() 的计算公式为:
的计算公式为:
|
|
(6.5a) |
式中, ![]() (mm)为梁的有效高度;
(mm)为梁的有效高度; ![]() (MPa)受拉钢筋的弹性模量;
(MPa)受拉钢筋的弹性模量; ![]() (mm)为钢筋周长,
(mm)为钢筋周长, ![]() (mm)为FRP粘贴宽度;
(mm)为FRP粘贴宽度; ![]() 为截面弯矩;
为截面弯矩;
|
|
(6.5b) |
其中, ![]() ,
, ![]() 为混凝土受压区高度,如图6-5所示。
为混凝土受压区高度,如图6-5所示。
|
|
(6.5c) |
其中, ![]() (mm2)和
(mm2)和 ![]() (mm2)分别为受拉钢筋和FRP截面积。
(mm2)分别为受拉钢筋和FRP截面积。
由 ![]() 受弯剥离条件,就可以由式(6.5a)直接计算出相应的极限弯矩
受弯剥离条件,就可以由式(6.5a)直接计算出相应的极限弯矩 ![]() ,当然
,当然 ![]() 应小于FRP拉断弯矩
应小于FRP拉断弯矩 ![]() 。
。
在fib的附录中,还给了另一个剥离承载力的计算模型,但是由于该模型非常复杂,事实上几乎无法用于实际工程计算,因此,在本文中不予讨论。
6.4.7 不同设计公式和计算结果的对比
在上述公式中,ACI 440
[2] ,黄-叶 [133] 和Teng et al.
[112] 的模型直接给出了IC debonding时FRP的应变 ![]() ,由平截面假定,可以直接计算得到相应受弯剥离破坏时截面弯矩
,由平截面假定,可以直接计算得到相应受弯剥离破坏时截面弯矩 ![]() 。JSCE [5] 建议的公式并未给出
。JSCE [5] 建议的公式并未给出
![]() ,但是它给出了FRP中的极限应力梯度
,但是它给出了FRP中的极限应力梯度 ![]() 。计算时需要验算FRP中的应力梯度,不断调整截面弯矩直至应力梯度小于界限值。由fib [4] 建议的设计公式也未给出
。计算时需要验算FRP中的应力梯度,不断调整截面弯矩直至应力梯度小于界限值。由fib [4] 建议的设计公式也未给出
![]() ,它给出了IC debonding和弯曲裂缝宽度
,它给出了IC debonding和弯曲裂缝宽度 ![]() 之间的关系,并给出了弯曲裂缝宽度的计算公式,进而通过剥离破坏时的界限裂缝宽度由式(6.5a)来确定
之间的关系,并给出了弯曲裂缝宽度的计算公式,进而通过剥离破坏时的界限裂缝宽度由式(6.5a)来确定 ![]() 。
。
以6.2节收集的80个IC debonding试验资料为基础,用上述不同设计公式计算得到的受弯剥离承载力见图6-6和表6-1,其中, ![]() 为受弯剥离承载力试验值,
为受弯剥离承载力试验值, ![]() 为FRP拉断时的极限弯矩。由对比可以看出,ACI,JSCE和fib的公式在
为FRP拉断时的极限弯矩。由对比可以看出,ACI,JSCE和fib的公式在 ![]() 小于
小于 ![]() 时会过高估计受弯剥离承载力,而且计算结果非常离散,这是很不安全的,可以说这些公式都不适用于计算IC debonding问题。而Teng et al.和黄-叶的模型计算结果就要好一些,但是这两个模型都显然过于保守。
时会过高估计受弯剥离承载力,而且计算结果非常离散,这是很不安全的,可以说这些公式都不适用于计算IC debonding问题。而Teng et al.和黄-叶的模型计算结果就要好一些,但是这两个模型都显然过于保守。
由前述分析,受弯剥离和剪力及裂缝张开量都有关,而现有的设计公式,如JSCE公式只考虑了剪力引起的剥离破坏,而fib公式只考虑了裂缝张开引起的剥离破坏,都是不全面的;ACI公式完全基于试验结果回归,对受弯剥离破坏的内在机理缺乏认识,通用性不好,因而这三个模型的计算结果和试验结果差异很大。
由于试验应变片密度有限,很难准确测量裂缝位置处FRP的应变分布,因而量测值往往比真实值要小,所以基于实测FRP应变的Teng et al.公式预测的剥离弯矩比试验结果普遍偏小。而黄-叶公式由于当时对界面剥离性能认识程度的限制,所以只能偏保守估计界面强度,所以预测结果也比试验结果要小。
因此,综上所述,现阶段还没有一个能够很好预测IC debonding受弯剥离破坏的设计公式。
表6-1 不同模型计算结果对比
|
模型名称 |
平均误差 |
平均绝对误差 |
均方差 |
|
15.07% |
18.43% |
0.205 |
|
|
Teng et al.公式 [112] |
-24.96% |
25.18% |
0.129 |
|
黄-叶公式 [133] |
-20.40% |
22.32% |
0.171 |
|
日本JSCE公式 [5] |
12.33% |
19.05% |
0.211 |
|
-5.10% |
33.86% |
0.489 |
![(a) 美国ACI 公式 [2]](./06.files/image156.gif)
(a) 美国ACI 公式 [2]
![(b) Teng et al. 公式 [112]](./06.files/image158.gif)
(b) Teng et al. 公式 [112]
![(c) 黄-叶公式 [133]](./06.files/image160.gif)
(c) 黄-叶公式 [133]
![(d) 日本JSCE公式 [5]](./06.files/image162.gif)
(d) 日本JSCE公式 [5]
![(e) 欧洲fib公式 [4]](./06.files/image164.gif)
图 6-6 不同公式计算的剥离弯矩与试验结果比较
6.5 小结
本章对受弯加固剥离的破坏形式,试验研究和数值分析研究,以及现有的受弯剥离承载力计算方法进行了回顾和总结。从现有研究中可以看出,目前对受弯剥离的试验研究已经进行的比较充分了,但是数值模拟和承载力设计公式的研究都进行得很不够。存在的主要问题包括:
(1) 由于对FRP-混凝土界面粘结-滑移本构关系的认识不足,受弯剥离界面模型缺少依据;
(2) 弥散裂缝模型难以准确估计裂缝附近的滑移集中,而分离裂缝模型又难以克服网格重划分的困难,因而现在还没有一个有限元模型可以很好的模拟受弯剥离破坏问题;
(3) 由于现阶段有关受弯剥离承载力计算的各种设计公式都或多或少地在反映受弯剥离机理方面存在不足,计算结果与试验结果的对比均存在较大误差。其中ACI,JSCE和fib的公式计算结果的离散性很大,且明显偏于不安全。黄-叶公式和Teng et al.公式的计算结果则过于保守,且离散性也比较大。
综上,有必要在前文提出的界面粘结-滑移行为的研究基础上,提出能够真实反映受弯剥离的有限元模型,进而根据有限元模型以及试验得到的粘结应力分布规律,提出符合受弯剥离破坏内在机理的分析模型,并简化得到合理的设计公式。
|
目 录 |
I |
|
I |
|
|
1 |
|
5 |
|
25 |
|
41 |
|
59 |
|
80 |
|
94 |
|
134 |
|
150 |
|
178 |